
八票清年大学报自然科样年第春范 hip cinjm 复合材料固化过程中温度及应变场分布的解析解 李君,姚学锋,刘应华,寇暂君己,戴棣 (1.清华大学工程力学系,北京1000842北京航空制造工程研究所,北京100024 摘 要:针对复合材料层合板结构件的制造工艺过程,避立 都环境温度的变化,以及层合板内部固化反应出现 简化的 维层合板结构件的瞬态热传导方程:基于典型的 的化学放热现象在层合板内部将产生复杂的温度 团化工艺由线,推导出复合材料层合板结构件固化过程中的 温废场分布函数,并建立围化过程中的过余温度和B防数以 梯度这种不均匀分布的温度场,不仅会引起复合材 料的固化不均匀,而且还将在复合材科内产生热应 及Fourier数的关系;绘制出层合板结构件厚度方向在典型 力和变形,从而导致复合材料的早期破坏因此,研 化工方下中心线上置度场分布的Hr图然后苯 出层合 结构件在国化过程中导致的 究复合材料层合板在固化工艺过程中板内温度分布 及其变化规律,对提高复合材料工艺质量有重要意 温度相不 大:对 于保 阶 ,结构件内部温度出现显著的 义 峰值 目前对于复合材料层合板固化过程中的研究计 关键词:固化:瞬态热传到;Heisler图 算主要是采用有限元方法进行处理h等"运用 中图分类号:TB33 文献标识码:A 有限元方法研究了结构固化过程中的温度及固化度 文音编号:100000544200g05012605 的分布;L运用粘弹性方法研究了不同的温度 边界条件对结构件翘曲变形的影响。此外还有张纪 An analytic approach for the temperature 奎阎勇“等都运用FEA研究了结构固化过程中 fields and the strain of composite 的温度场分布但是运用有限元方法(FEA进行计 laminate under curing 算时,必须知道热压罐内部的温度分布、对流换热的 LI Jun.YAO Xuefeng. 相关参数,树脂纤维以及模具的热力学材料参数 KOU Zhejun?.DAI Di 等,才能获得结构件内部的温度随时间和空间的变 化关系这样对于工程师的实际坛用就存在一定的 B附jiag10o084ia 困难随着传热学的发展,人们开始将其运用到此领 域,如Mote研究了层合板内的解态热传导问题 本文主要基于一维瞬态热传导方程,建立复合 材料层合板结构件固化过程中的温度场分布函数 以及固化过程中的过余温度和Bot Fourier数的关 the te ature function for 系进一步绘制层合板中心温度场的Heisler图,并 er cunng was denv e 研究不同的升温速率和过余温度的关系,然后基于 nd the 温度场分布计算出层合板结构件在固化过程中导致 he part in the of the hold and ramp stage. Based on the 的内部应变场分布 but in the hold stage.the internal emperature reached to a poak Key words curing transient heat conduction:Heisler chart 收精日期:2008-07-21 基金项目:国家自然科学基金资助项目(10772094 作者简介: 李君(198什),男),江苏,博士研究生 ,复合材料层合板在固化过程中,申于层合板外b通翻联系人姚特锋,测教轻下严伦和民网乐四
ISSN 1000-0054 CN 11-2223 /N 清华大学学报 (自然科学版 ) J Tsingh ua Univ ( Sci & Tech ), 2009年 第 49卷 第 5期 2009, Vo l. 49, No. 5 w 28 http: / /qhx bw. chinajo urnal. net. cn 复合材料固化过程中温度及应变场分布的解析解 李 君 1 , 姚学锋 1 , 刘应华 1 , 寇哲君 2 , 戴 棣 2 ( 1. 清华大学 工程力学系 , 北京 100084; 2. 北京航空制造工程研究所 , 北京 100024) 收稿日期: 2008-07-21 基金项目: 国家自然科学基金资助项目 ( 10772094) 作者简介: 李君 ( 1980— ) , 男 (汉 ) , 江苏 , 博士研究生。 通讯联系人: 姚学锋 , 副教授 , E-mail: yx f@ mail. tsinghua. ed u. cn 摘 要: 针对复合材料层合板结构件的制造工艺过程 ,建立 简化的一维层合板结构件的瞬态热传导方程; 基于典型的 固化工艺曲线 ,推导出复合材料层合板结构件固化过程中的 温度场分布函数 ,并建立固化过程中的过余温度和 Biot 数以 及 Fourier数的关系 ; 绘制出层合板结构件厚度方向在典型 固化工艺方案下中心线上温度场分布的 Heisler图 ,然后基 于温度场分布计算出层合板结构件在固化过程中导致的内 部应变场分布 ,研究表明 ,对于升 (降 )阶段 ,中心温度和边界 温度相差不大; 对于保温阶段 ,结构件内部温度出现显著的 峰值。 关键词: 固化; 瞬态热传到 ; Heisler图 中图分类号: TB 33 文献标识码: A 文章编号: 1000-0054( 2009) 05-0126-05 An analytic approach for the temperature f ields and the strain of composite laminate under curing LI Jun1 , YAO Xuefeng 1 , LIU Yinghua1 , KOU Zhejun 2 , DAI Di 2 ( 1. Department of Engineering Mechani cs, Tsinghua University, Beijing 100084, China; 2. Beijing Aeronautical Manufacturing Technology Research Institute, Beijing 100024, China) Abstract: According t o th e cu ring process of composite laminat e, a simplifi ed one-dimensi onal transient heat conduction equati on f or th e composit e laminat e w as est ablish ed. Based on a t ypi cal curing t ech nology cu rve, th e t emp erature function f or th e com posit e laminat e structure under cu ring w as deriv ed. The relation ship w as established among the su rplus t emperature and the Bio t num ber, Fouri er num ber; and th en provid es Heisler ch ar t f or th e midplane of th e part in the case of th e h old and ram p stage. Based on th e t emperatu re fi eld, the strain fi eld w as calcu lated. The res ult show s th at int ernal t emperature closed to th e bound ary in the ramp stage, but in the hold stage, the in ternal temperature reached to a peak v alue. Key words: cu ring; transi en t heat conduction; Heisl er chart 复合材料层合板在固化过程中 ,由于层合板外 部环境温度的变化 ,以及层合板内部固化反应出现 的化学放热现象 ,在层合板内部将产生复杂的温度 梯度。这种不均匀分布的温度场 ,不仅会引起复合材 料的固化不均匀 ,而且还将在复合材料内产生热应 力和变形 ,从而导致复合材料的早期破坏。 因此 ,研 究复合材料层合板在固化工艺过程中板内温度分布 及其变化规律 ,对提高复合材料工艺质量有重要意 义。 目前对于复合材料层合板固化过程中的研究计 算主要是采用有限元方法进行处理。 Zhu等 [1 ]运用 有限元方法研究了结构固化过程中的温度及固化度 的分布; Lee [2 ]运用粘弹性方法研究了不同的温度 边界条件对结构件翘曲变形的影响。 此外还有张纪 奎 [3 ] 、阎勇 [4 ]等都运用 FEA研究了结构固化过程中 的温度场分布。 但是运用有限元方法 ( FEA)进行计 算时 ,必须知道热压罐内部的温度分布、对流换热的 相关参数 ,树脂、纤维以及模具的热力学材料参数 等 ,才能获得结构件内部的温度随时间和空间的变 化关系。 这样对于工程师的实际运用就存在一定的 困难。随着传热学的发展 ,人们开始将其运用到此领 域 ,如 Mo nte [ 5]研究了层合板内的瞬态热传导问题。 本文主要基于一维瞬态热传导方程 ,建立复合 材料层合板结构件固化过程中的温度场分布函数 , 以及固化过程中的过余温度和 Biot、 Fourier数的关 系 ,进一步绘制层合板中心温度场的 Heisler图 ,并 研究不同的升温速率和过余温度的关系 ,然后基于 温度场分布计算出层合板结构件在固化过程中导致 的内部应变场分布
李君,等:复合材料固化过程中温度及应变场分布的解析解 127 1理论模型 于板的中心截面上,因此 因为层合板结构件的长度和宽度远大于其厚 基于以上的瞬态热传导方程,将解分解成渐近 度,因而平板的长度和宽度的边缘向四周的散热对 (特解)和瞬态解,即 平板内的温度分布复形响很小,所以把问题简化为一 维问题 T=T.+T.. (5) 其中工代表渐近解,T代表瞬态解 设层合板固化过程中温度边界条件为经典的固 1)渐近解 化温度曲线,如图1所示 渐近解假设为下面的表达式: 500 T=A(1+B( (6) 其中A(a)B(为空间坐标系a的函数 将渐近解式(6)代入一维瞬态热传导方程(1)及 兰 350 边界条件得渐近解T,为 300 2506 4 (7) 图1复合材料固化过程边界温度曲线 其中, 11温度场分布的理论模型 R= (0-rL2 0=05+ (8) 11.1升(降)温阶段的理论模型 Bi为ot数,即量纲为一的板的厚度 层合板结构件厚度方向的一维热传导方程及边 B=长 (9) 界条件如下: H= 2)解态解 由于解T=T+T,其中T满足所有的方程和 H=-装(T-),a=+1>&(② 边界条件,因此将T,代入方程(1厂(3)得 =+长(T-,a->G II ,1>0,|40 (11) 其中:为固化过程中单位时间内单位体积的树脂 放热量,由差示扫描量热(DsC)获得,Q=Q,d a=-1,1>0 (12) 为复合材料的密度;为复合材料的比热容;r为 对于式(10一(12运用分离变量法得 升(降)温速率:K为层合板厚度方向等效导热系 Ecos(a)p(-Fo) (13) 数;L为层合板厚度:T为热扩散系数,无 其中:入为方程 为层合板厚度方向量纲为1的坐标,层合板结构示 tand)=,i=1,2,3,4 (14) 意图如图2所示,边界条件为对流边界条件x轴置 的特征值,可通过图解法求得:Fo为Fourier数,即 量纲为一的时间, =是 (15) 为了求解E,运用初始条件,由式(5)及(7得 70=T-lo=--}+ h (16) 1994.层合板不维热传导结构示意图cctronic Publishing 又由式(3)得s reserved.. http://www.cnki.net
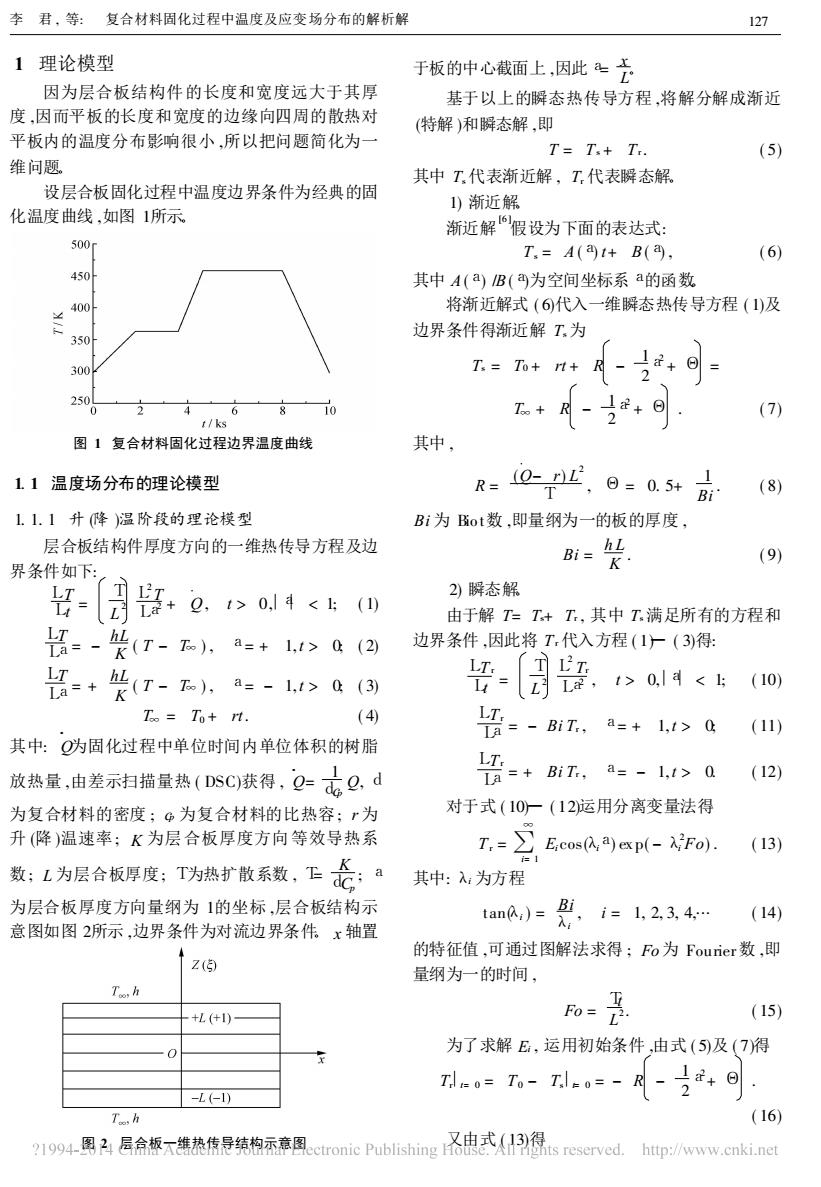
1 理论模型 因为层合板结构件的长度和宽度远大于其厚 度 ,因而平板的长度和宽度的边缘向四周的散热对 平板内的温度分布影响很小 ,所以把问题简化为一 维问题。 设层合板固化过程中温度边界条件为经典的固 化温度曲线 ,如图 1所示。 图 1 复合材料固化过程边界温度曲线 1. 1 温度场分布的理论模型 1. 1. 1 升 (降 )温阶段的理论模型 层合板结构件厚度方向的一维热传导方程及边 界条件如下: LT Lt = T L 2 L 2 T La 2 + Q , t > 0,|a| 0; ( 2) LT La = + hL K ( T - T∞ ) , a= - 1,t > 0; ( 3) T∞ = T0 + rt. ( 4) 图 2 层合板一维热传导结构示意图 其中: Q · 为固化过程中单位时间内单位体积的树脂 放热量 ,由差示扫描量热 ( DSC)获得 , Q · = 1 dcp Q, d 为复合材料的密度 ; cp 为复合材料的比热容; r 为 升 (降 )温速率; K 为层合板厚度方向等效导热系 数; L 为层合板厚度; T为热扩散系数 , T= K dCp ; a 为层合板厚度方向量纲为 1的坐标 ,层合板结构示 意图如图 2所示 ,边界条件为对流边界条件。 x 轴置 于板的中心截面上 ,因此a= x L 。 基于以上的瞬态热传导方程 ,将解分解成渐近 (特解 )和瞬态解 ,即 T = Ts + Tr . ( 5) 其中 Ts代表渐近解 , Tr 代表瞬态解。 1) 渐近解。 渐近解 [6 ]假设为下面的表达式: Ts = A (a) t+ B (a) , ( 6) 其中 A (a) /B (a)为空间坐标系a的函数。 将渐近解式 ( 6)代入一维瞬态热传导方程 ( 1)及 边界条件得渐近解 Ts为 Ts = T0 + rt + R - 1 2 a 2 + Θ = T∞ + R - 1 2 a 2 + Θ . ( 7) 其中 , R = (Q - r) L 2 T , Θ= 0. 5+ 1 Bi . ( 8) Bi 为 Bio t数 ,即量纲为一的板的厚度 , Bi = h L K . ( 9) 2) 瞬态解。 由于解 T= Ts+ Tr , 其中 Ts满足所有的方程和 边界条件 ,因此将 Tr 代入方程 ( 1)— ( 3)得: LTr Lt = T L 2 L 2 Tr La 2 , t > 0,|a| 0; ( 11) LTr La = + Bi Tr , a= - 1,t > 0. ( 12) 对于式 ( 10)— ( 12)运用分离变量法得 Tr = ∑ ∞ i= 1 Ei cos(λia) ex p( - λ 2 i Fo) . ( 13) 其中: λi 为方程 tan(λi ) = Bi λi , i = 1, 2, 3, 4,… ( 14) 的特征值 ,可通过图解法求得 ; Fo 为 Fourier数 ,即 量纲为一的时间 , Fo = Tt L 2 . ( 15) 为了求解 Ei , 运用初始条件 ,由式 ( 5)及 ( 7)得 Tr|t= 0 = T0 - Ts|t= 0 = - R - 1 2 a 2 + Θ . ( 16) 又由式 ( 13)得 李 君 , 等: 复合材料固化过程中温度及应变场分布的解析解 127

128 清华大学学报伯然科学版) 2009.49(5 (17) [O,T△T(a4--). 由于cos()为正交函数,两边同乘 cos(),后积分得 M B=-A-+ (18 M 2,2西aTd-i以 其中, 「+1 cos(a)da (24) (i=1,2,34…)月 cos(a da 其中。 cosa,a)da [Ok,= 0 C2 X= (=1,2,34…) T (19の (a,= 因此复合材料层合板固化过程中的温度场T为 T=T+T=五+月-}4回 进一步由层合板的本构方程式(25)可以得出结 构件固化过程中导致的结构件中面应变及曲率 N AnAn (20 N An An 0 进一步得复合材料层合板固化过程中的过余温度 N 0 M D M〉= k 0=T-=月 (25) L Dis D36 Dod k 其中 (21) 4-d(-a). 则板的中心(是0)过余温度为 0=T-T =2店-) 2复合材料固化过程中的Heisler图及应变 场的计算 (22) 由升降温阶段的分析可以发现入,入2,入3… 11.2保温阶段 入为递增数列,因此入愈大级数中后面项的作用与 对于保温阶段,问题可进一步的简化,则温度函 前面项的作用相比就愈小除此之外,F愈大,随 数T.=工=T,运用升(降)温阶段相同方法得过 着标号n的增加,级数减小得愈快 余温度为 研究表明,当F≥03.式(22)或(23收敛得很 0=T-T= 快,此时用级数的第一项描述温度分布就己经足够 (To-T Xcos(a)exp(-XFo).(23) 精确了.因此将式(19代入式(22以(23)中并只考 虑级数的第一项得简化的过余温度 其中具体的参数定义同升温阶段一致 2.1升(降温阶段的过余温度 1.2固化引起结构件的翘曲变形 根据层合板理论,由于固化过程中内部温度变 0=T-T=- 化导致的叠层复合材料的广义内力与广义内力矩 3i成+od1-4sin× 01 China Academic Jourmal Electronie Publishing House.p:ww.nki.net
R - 1 2 a 2 + Θ = ∑ ∞ i= 1 Ei cos(λia). ( 17) 由 于 { cos (λia) } 为 正 交 函 数 , 两 边 同 乘 cos(λia) , 后积分得 Ei = - R - 1 2 vi + ΘXi . ( 18) 其中 , vi =∫ + 1 - 1a 2 co s(λia) da ∫ + 1 - 1 cos 2 (λia) da , (i = 1, 2, 3, 4,… ); Xi =∫ + 1 - 1 cos(λia)da ∫ + 1 - 1 cos 2 (λia) da , (i = 1, 2, 3, 4,… ). ( 19) 因此复合材料层合板固化过程中的温度场 T为 T = Ts + Tr = T∞ + R - 1 2 a 2 + Θ - ∑ ∞ i= 1 R - 1 2 vi + ΘXi co s(λia) ex p( - λ 2 i Fo ). ( 20) 进一步得复合材料层合板固化过程中的过余温度θ 为 θ= T - T∞ = R - 1 2 a 2 + Θ - ∑ ∞ i= 1 R - 1 2 vi + ΘXi co s(λia) ex p( - λ 2 i Fo ). ( 21) 则板的中心 (a= 0)过余温度为 θ= T - T∞ = RΘ- ∑ ∞ i= 1 R - 1 2 vi + ΘXi ex p( - λ 2 i Fo ). ( 22) 1. 1. 2 保温阶段 对于保温阶段 ,问题可进一步的简化 ,则温度函 数 Ts= T∞ = T1 , 运用升 (降 )温阶段相同方法得过 余温度为 θ= T - T1 = ( T0 - T1 )∑ ∞ i= 1 Xi cos(λia) ex p( - λ 2 i Fo) . ( 23) 其中具体的参数定义同升温阶段一致。 1. 2 固化引起结构件的翘曲变形 根据层合板理论 ,由于固化过程中内部温度变 化导致的叠层复合材料的广义内力与广义内力矩 为: N * x N * y N * xy = ∑ n k= 1 [Q - ](k ) {T-}(k)ΔT (zk - zk- 1 ) , M * x M * y M * xy = 1 2∑ n k= 1 [Q - ]( k) {T- }(k )ΔT (z 2 k - z 2 k- 1 ). ( 24) 其中 , [Q - ](k ) = Q11 Q12 Q16 Q12 Q22 Q26 Q16 Q26 Q66 (k ) , {T-}(k ) = Tx Ty Txy ( k) . 进一步由层合板的本构方程式 ( 25)可以得出结 构件固化过程中导致的结构件中面应变及曲率。 Nx Ny Nx y = A11 A12 0 A12 A22 0 0 0 A66 Xx Xy Vx y , Mx My Mx y = D11 D12 D16 D12 D22 D26 D16 D26 D66 kx ky kxy . ( 25) 其中: Aij = ∑ n k= 1 Q k i j (zk - zk - 1 ) , Dij = 1 3∑ n k= 1 Q k ij (z 3 k - z 3 k- 1 ) . 2 复合材料固化过程中的 Heisler图及应变 场的计算 由升 (降 )温阶段的分析 ,可以发现λ1 ,λ2 ,λ3 ,… , λn 为递增数列 ,因此λi 愈大 ,级数中后面项的作用与 前面项的作用相比就愈小。 除此之外 , Fo愈大 ,随 着标号 n的增加 ,级数减小得愈快。 研究表明 ,当 Fo≥ 0. 3, 式 ( 22)或 ( 23)收敛得很 快 ,此时用级数的第一项描述温度分布就已经足够 精确了。 因此将式 ( 19)代入式 ( 22)、 ( 23)中并只考 虑级数的第一项得简化的过余温度。 2. 1 升 (降 )温阶段的过余温度 θ= T - T∞ = - Θ 2sinλ1 λ1+ sinλ1 cosλ1 - 2λ 2 1 sinλ1+ 4λ1 co sλ1 - 4sinλ1 2λ 2 1 (λ1 + sinλ1 cosλ1 ) × 128 清 华 大 学 学 报 (自 然 科 学 版 ) 2009, 49( 5)

李君,等:复合材料固化过程中温度及应变场分布的解析解 129 Rcos(A:a)xp(-λiFo)+ 月-+ cosa,a)gp(-λiFo), (29) 则层合板中心(色0)的过余温度函数为 (26 则层合板中心(在0)的过余温度函数为 0=T-T,= 2sim 2s, 0。=T。-=- (T-)siexp(-xiFo).(30) 2isid+4co1=4id× 由上式可以发现,对于保温阶段,过余温度只是F0 X1+si1oo以) 的函数 Rexp(-AiFo)+Θ (27 2.3预浸料固化成型层合板结构件中心线上温度 由上式可以看出,当Foo∞时, 分布Heisler图 0=阳=月0.5+ (28) 本文采用A43501-6预浸料固化成型,相关厚 度方向的等效材料参数见表1,固化过程中的热压 22保温阶段的过余温度 罐温度如图1所示 251 0=T-T=(T-T)人+sik1o 表1复合材料AS4/3501-6层合板厚度方向等效材料参数) d K./ 01 (kg m (IkK) (Wrm”) (m2 (W m2 K-) (kJkg) 1578 870 0.69 010 30 1986 将相关材料参数代入过余温度的表达式(26)及 Ri 式(27),其中特征值入,和毕渥数Bi可以从相关手册 上查得,绘制出层合板厚度方向中心处的Hei sler 图,以及不同的升温速率和过余温度的关系,如图 子5所示 0.,12 0.10 0.08 0.000 0.06 (aT=363K 0.0 (ar=0.0361K/s 0.15 -000 6 010 图4不同Biot Fourier数保温阶段Heislere图 2.4AS4/35016复合材料层合板结构件固化过程 导致的中面应变及曲率 AS4/3501-6复合材料层合板的铺层方式为 b)r=-0.08K1s [450/-45/90145/0/45/0k,单层板厚度为025 男孕不同Frie数升降漫Hekr图ni Publis由王树脂酮化过程牛,开始处于精性流动状态c
Rcos(λ1a) ex p( - λ 2 1Fo) + R - 1 2 a 2 + Θ . ( 26) 则层合板中心 (a= 0)的过余温度函数为 θm = T m - T∞ = - Θ 2sinλ1 λ1 + sinλ1 cosλ1 - 2λ 2 1 sinλ1 + 4λ1 cosλ1 - 4sinλ1 2λ 2 1 (λ1+ sinλ1 cosλ1 ) × R ex p( - λ 2 1Fo) + RΘ. ( 27) 由上式可以看出 ,当 Fo→∞时 , θms = RΘ= R 0. 5+ 1 Bi . ( 28) 2. 2 保温阶段的过余温度 θ= T- T1= ( T0- T1 ) 2sinλ1 λ1+ sinλ1 co sλ1 × cos(λ1a) ex p( - λ 2 1Fo) , ( 29) 则层合板中心 (a= 0)的过余温度函数为 θ= T - T1 = ( T0 - T1 ) 2sinλ1 λ1+ sinλ1 cosλ1 exp( - λ 2 1Fo) . ( 30) 由上式可以发现 ,对于保温阶段 ,过余温度只是 Fo 的函数。 2. 3 预浸料固化成型层合板结构件中心线上温度 分布 Heisler图 本文采用 AS4 /3501-6预浸料固化成型 ,相关厚 度方向的等效材料参数见表 1, 固化过程中的热压 罐温度如图 1所示。 表 1 复合材料 AS4 /3501-6层合板厚度方向等效材料参数 [7] d/ ( kg m - 3 ) cp / ( J kg - 1 K - 1 ) Kz / ( W m - 1 K - 1 ) Tz / ( m 2 s - 1 ) h / ( W m - 2 K - 1 ) Q / ( k J kg - 1 ) 1 578 870 0. 69 0. 5× 10 - 6 30 198. 6 将相关材料参数代入过余温度的表达式 ( 26)及 式 ( 27) , 其中特征值λi 和毕渥数B i可以从相关手册 上查得 ,绘制出层合板厚度方向中心处的 Heisler 图 ,以及不同的升温速率和过余温度的关系 ,如图 3— 5所示。 图 3 不同 Biot、 Fourier数升 (降 )温 Heisler图 图 4 不同 Biot、 Fourier数保温阶段 Heisler图 2. 4 AS4 /3501-6复合材料层合板结构件固化过程 导致的中面应变及曲率 AS4 /3501-6 复合材料层合板的铺层方式为 [45 /0 /-45 /90 /45 /0 /-45 /0 ]s , 单层板厚度为 0. 25 mm。由于树脂固化过程中 ,开始处于粘性流动状态 , 李 君 , 等: 复合材料固化过程中温度及应变场分布的解析解 129

清华大学学报伯然科学版) 2009.49(5) 0.15 固化导致的内应力得到很快的释放因此最终的翘 曲变形是由于保温阶段2产生的过余温度及冷却温 .0200 0.10 度叠加的结果AS435016复合材料性能参数如表 2所示 对于层合板结构件,由于很薄,其厚度方向的尺 寸相对于平面内温度来说,很小,因此假设厚度方向 温度分布为均匀的温度分布,对于冷却过程,温度变 化AT160K,如图1所示并且由于层合板结构件 8 10 为对称铺层,因此由固化温度变化导致的结构件内 图5不同升温速率下过余温度和Fourier数之间的关系 力矩(M为零 表2AS4/3501-6复合材料性能参数 E2.E Ge.Gp.Ga CTE CTE.CTE V23V3 GPa GPa GPa 10X℃- 1XC” 0.30 033 135 88 447 34 最后将相关材料参数代入后计算得复合材料层 2 1 合板结构件固化导致的中面的应变分量为: .20 0.3 k [3】张纪车,关志东,鄙正能.热圆性复合材料圆化过程中温度 = 10×-1.0 了k}=0 场的三编有限元分析小复合材料学报,2006.232水175 -179. 3.5 k ZHANG Jkui. GUAN Zhidong.LI Zhengneng 3结论 ites during cure process Ac )对于升温阶段,结构件内部的温度和边界条 件差别较小,但是对于保温固化阶段,结构件内部的 温度则显著超出热压罐中的温度,此结论和文【 4 图勇,庄范正刚等,铺脂比热容对复合材料圆化过 数值模拟的影响[小航空材料学报,2006.26237-40 中的有限元计算结果一致,证明了本简化方法的正 YAN Yong」 ,ZHU ANG Zhuo.ZHO U mgmg,etl 确性 Efect of specific heat of thermal resin on simulation o 2)对于固化升温阶段,在一定的Biot数(量纲 262 37=40n 为一的厚度)下,不同的固化升温速率对结构件内部 Mon nt heat 的过余温度有一定的影响,但是比较的小 3)复合材料结构件内部的温度随着Fourier数 6073610 量纲为1的时间)的增加而趋于热压罐中的温度 [6] Rasekh A Ffficient methods for non-iner thermochemica 4)由于由于对称的铺层方式,复合材料层合板 analysis of composite structures undergoing autoelave 在固化过程中,不产生中面内的曲率的变化,但是存 [D)Canada The Uriverity of British 在中面应变分量而且选择不同的铺层方式后,可 2007 [71 Zobeiry N.Viscoelasticity constitut ive modeks for evaluatio 能产生负的热应变 sn eD] 参考文献(References) 1]ZhuQ.Ceubelle P H Dimensional accura 点man ?1994-2014 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 5 不同升温速率下过余温度和 Fourier数之间的关系 固化导致的内应力得到很快的释放 ,因此最终的翘 曲变形是由于保温阶段 2产生的过余温度及冷却温 度叠加的结果。 AS4 /3501-6复合材料性能参数如表 2所示。 对于层合板结构件 ,由于很薄 ,其厚度方向的尺 寸相对于平面内温度来说 ,很小 ,因此假设厚度方向 温度分布为均匀的温度分布 ,对于冷却过程 ,温度变 化Δ T= 160 K, 如图 1所示。并且由于层合板结构件 为对称铺层 ,因此由固化温度变化导致的结构件内 力矩 { M * }为零。 表 2 AS4 /3501-6复合材料性能参数 v 23 ,v13 v12 E1 GPa E2 , E3 GPa G12 , G13 , G23 GPa C TE1 10 - 6×℃- 1 CTE2 , CTE3 10 - 6×℃- 1 0. 30 0. 33 135 8. 8 4. 47 2 34 最后将相关材料参数代入后计算得复合材料层 合板结构件固化导致的中面的应变分量为: Xx Xy Vxy = 10 - 3× 0. 3 - 1. 0 3. 5 , kx ky kxy = O. 3 结 论 1) 对于升温阶段 ,结构件内部的温度和边界条 件差别较小 ,但是对于保温固化阶段 ,结构件内部的 温度则显著超出热压罐中的温度 ,此结论和文 [ 1] 中的有限元计算结果一致 ,证明了本简化方法的正 确性。 2) 对于固化升温阶段 ,在一定的 Bio t数 (量纲 为一的厚度 )下 ,不同的固化升温速率对结构件内部 的过余温度有一定的影响 ,但是比较的小。 3) 复合材料结构件内部的温度随着 Fourier数 (量纲为 1的时间 )的增加而趋于热压罐中的温度。 4) 由于由于对称的铺层方式 ,复合材料层合板 在固化过程中 ,不产生中面内的曲率的变化 ,但是存 在中面应变分量; 而且选择不同的铺层方式后 ,可 能产生负的热应变。 参考文献 ( References) [1 ] Zh u Q, Geubelle P H. Dimensional accuracy of thermoset composites: simulati on of process-induced residual stress es [ J]. Journal o f Com posit e Materia ls, 2001, 35( 24): 2171- 2205. [2 ] Lee S. Cure induced residual stresses in laminat ed cylind ri cal sh ells [ J]. K SME Int ernational Journal , 2000, 14( 1): 19 - 29. [3 ] 张纪奎, 关志东, 郦正能. 热固性复合材料固化过程中温度 场的三维有限元分析 [ J]. 复合材料学报 , 2006, 23( 2): 175 - 179. ZHANG Jikui, GUAN Zhidong , LI Zhengneng. Three-dim ensi onal finit e element anal ysis fo r th e t emperatu re fi eld of th ermos et composit es d uring cure process [ J]. Acta Materiae Com positae Sinica , 2006, 23( 2): 175 - 179. (in Chines e) [4 ] 阎勇, 庄茁 , 周正刚, 等 . 树脂比热容对复合材料固化过程 数值模拟的影响 [ J]. 航空材料学报 , 2006, 26( 2): 37- 40. YAN Yong , ZHU ANG Zhuo, ZHO U Zh eng gang , et al. Eff ect of specifi c heat of thermal resin on sim ulati on of composit e curing p rocess [ J]. Journal o f Aeronauti cal Materials, 2006, 26( 2): 37 - 40. ( in Chin ese) [5 ] Mon te F de. Transient h eat conduction in one-dimensional composit e slab: A `natural’ anal ytic approach [ J]. International Journal Heat an d Mass Tr ansf er, 2000, 43: 3607 - 3619. [6 ] Ras ekh A. Effi cient meth od s f or non-linear th ermochemi cal analysis of composite structu res undergoing autoclav e p rocessing [ D]. Canada: Th e Uni versit y of Britis h Columbia, 2007. [7 ] Zobeiry N. Viscoelasticit y constitutive models f or evaluation of residual stresses in th ermoset composites du ring cure [D]. Canada: Th e University of British Columbia, 2006: 93. 130 清 华 大 学 学 报 (自 然 科 学 版 ) 2009, 49( 5)