
高等传热学 第二章二维稳定导热 §1.解析法 一、导热系数为常数的精确解法 y个1=f)+ 只能解几何形状简单的物体 设: λ=Const 9,=0 微分方程: =0 Ox2 一个两面绝热的平板

高等传热学 8't 0"t 0=t-to 620 620 0 =0 (1) 2 Ox2 0y2 边界条件: x=0时,t=t。0=0 (a) x=时,t=t。0=0 (b) y=0时,t=t。0=0 (c) (2) y=b时,t=f(x)+t。0=f(x)(d) 用分离变量法,根据边界条件(2) 解出 (1) 的解为: 1n7 f(x)sin d = n (3) nπb sh
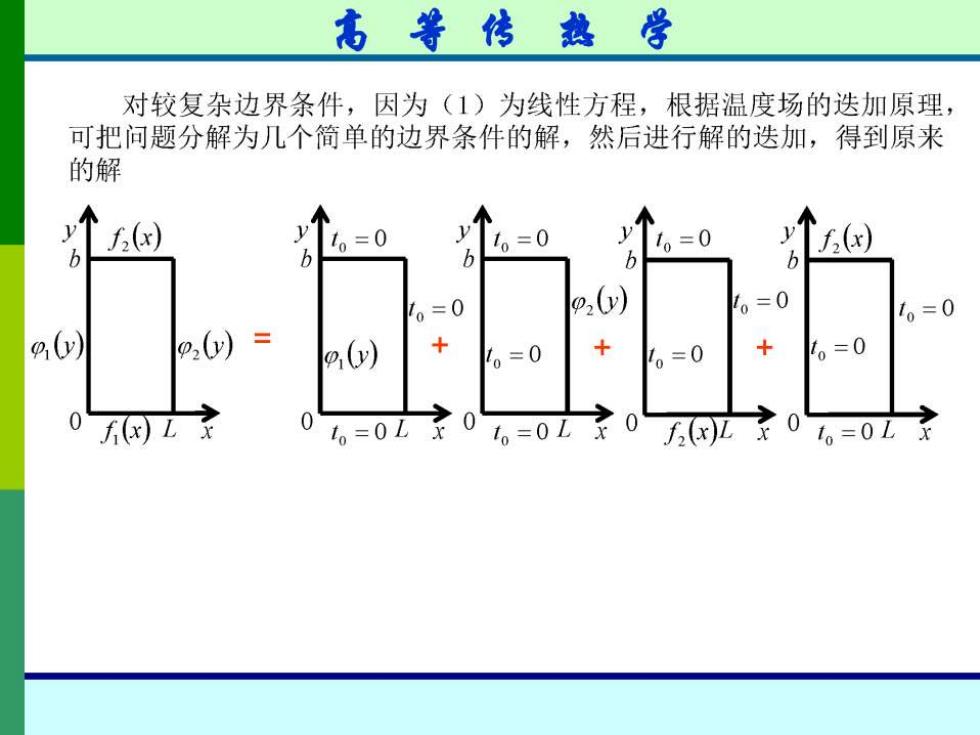
高等传热学 对较复杂边界条件,因为(1)为线性方程,根据温度场的迭加原理, 可把问题分解为几个简单的边界条件的解,然后进行解的迭加,得到原来 的解 f(x) =0 b 5 5 =0 v:(v) =0 10=0 c(v) y)= 1o=0 1。=0 1=0 0)L 0 t。=0Lx 0 0 t。=0L

高等传热学 ∂20 a20 ax2+ y2=0 y=0, 0=f0(x) 0=01+02+03+04 y=H, 日=fi(x) x=0, 0=po(y) X=6, 0=p1(y) a201,a201 a202,0202 8x F+ dy2 =0 0x dy2 =0 y=0, 01=0 y=0, 02=0 y=H, 01=0 y=H, 02=0 x=0, 01=0 x=0,02=p00y) X=6, 01=p10y) x=6, 82=0 a203,a203 dy2 -0 a204, 0x2+ 204-0 dy y=0, 03=0 y=0, 04=f6(x) y=H, 03=fi(x) y=H, 84=0 X=0, 83=0 x=0, 04=0 X=6 02=0 X三6, 04=0
高 等 传 热 学 𝜕 2𝜃 𝜕𝑥 2 + 𝜕 2𝜃 𝜕𝑦 2 =0 𝑦 = 0, 𝜃 = 𝑓0(𝑥) 𝑦 = 𝐻, 𝜃 = 𝑓1(𝑥) 𝑥 = 0, 𝜃 = 𝜑0(𝑦) 𝑥 = 𝛿, 𝜃 = 𝜑1(𝑦) 𝜃 = 𝜃1 + 𝜃2 + 𝜃3 + 𝜃4 𝜕 2𝜃1 𝜕𝑥 2 + 𝜕 2𝜃1 𝜕𝑦 2 =0 𝑦 = 0, 𝜃1 = 0 𝑦 = 𝐻, 𝜃1= 0 𝑥 = 0, 𝜃1= 0 𝑥 = 𝛿, 𝜃1 = 𝜑1(𝑦) 𝜕 2𝜃2 𝜕𝑥 2 + 𝜕 2𝜃2 𝜕𝑦 2 =0 𝑦 = 0, 𝜃2 = 0 𝑦 = 𝐻, 𝜃2= 0 𝑥 = 0, 𝜃2= 𝜑0(𝑦) 𝑥 = 𝛿, 𝜃2= 0 𝜕 2𝜃3 𝜕𝑥 2 + 𝜕 2𝜃3 𝜕𝑦 2 =0 𝑦 = 0, 𝜃3 = 0 𝑦 = 𝐻, 𝜃3= 𝑓1(𝑥) 𝑥 = 0, 𝜃3= 0 𝑥 = 𝛿, 𝜃3= 0 𝜕 2𝜃4 𝜕𝑥 2 + 𝜕 2𝜃4 𝜕𝑦 2 =0 𝑦 = 0, 𝜃4 = 𝑓0(𝑥) 𝑦 = 𝐻, 𝜃4= 0 𝑥 = 0, 𝜃4= 0 𝑥 = 𝛿, 𝜃4= 0

高等传热学 00 0(x,y)= 2 sh sim刘i)sn)x+ Jo sh(mm- 00 2 6 s行6切sin(x)ax+ mπ 00 2 mπ 品sh(T m(晋nm闭sm()西+ 2 了shg-刘 H mπ H sh7)
高 等 传 热 学 𝜃 𝑥, 𝑦 = 2 𝛿 𝑚=1 ∞ 𝑠ℎ( 𝑚𝜋𝑦 𝛿 ) 𝑠ℎ( 𝑚𝜋𝐻 𝛿 ) 𝑠𝑖𝑛( 𝑚𝜋 𝛿 𝑥) න 0 ∞ 𝑓1 𝑥 𝑠𝑖𝑛 𝑚𝜋 𝛿 𝑥 𝑑𝑥 + 2 𝛿 𝑚=1 ∞ 𝑠ℎ( 𝑚𝜋(𝐻 − 𝑦) 𝛿 ) 𝑠ℎ( 𝑚𝜋𝐻 𝛿 ) 𝑠𝑖𝑛( 𝑚𝜋 𝛿 𝑥) න 0 ∞ 𝑓0 𝑥 𝑠𝑖𝑛 𝑚𝜋 𝛿 𝑥 𝑑𝑥 + 2 𝐻 𝑚=1 ∞ 𝑠ℎ( 𝑚𝜋𝑥 𝐻 ) 𝑠ℎ( 𝑚𝜋𝛿 𝐻 ) 𝑠𝑖𝑛( 𝑚𝜋 𝐻 𝑦) න 0 ∞ 𝜑1 𝑥 𝑠𝑖𝑛 𝑚𝜋 𝛿 𝑦 𝑑𝑦 + 2 𝐻 𝑚=1 ∞ 𝑠ℎ( 𝑚𝜋(𝛿 − 𝑥) 𝐻 ) 𝑠ℎ( 𝑚𝜋𝛿 𝐻 ) 𝑠𝑖𝑛( 𝑚𝜋 𝐻 𝑦) න 0 ∞ 𝜑0 𝑥 𝑠𝑖𝑛 𝑚𝜋 𝛿 𝑦 𝑑𝑦

高等传热学 二、导热系数随温度变化的情况 1=f(x)+1o 设:=t) 9,=0 微分方程: b to (1) 0 因为微分方程(1)是非线性方程,因此,将微分方程线性化。 令: E=ad → 8t
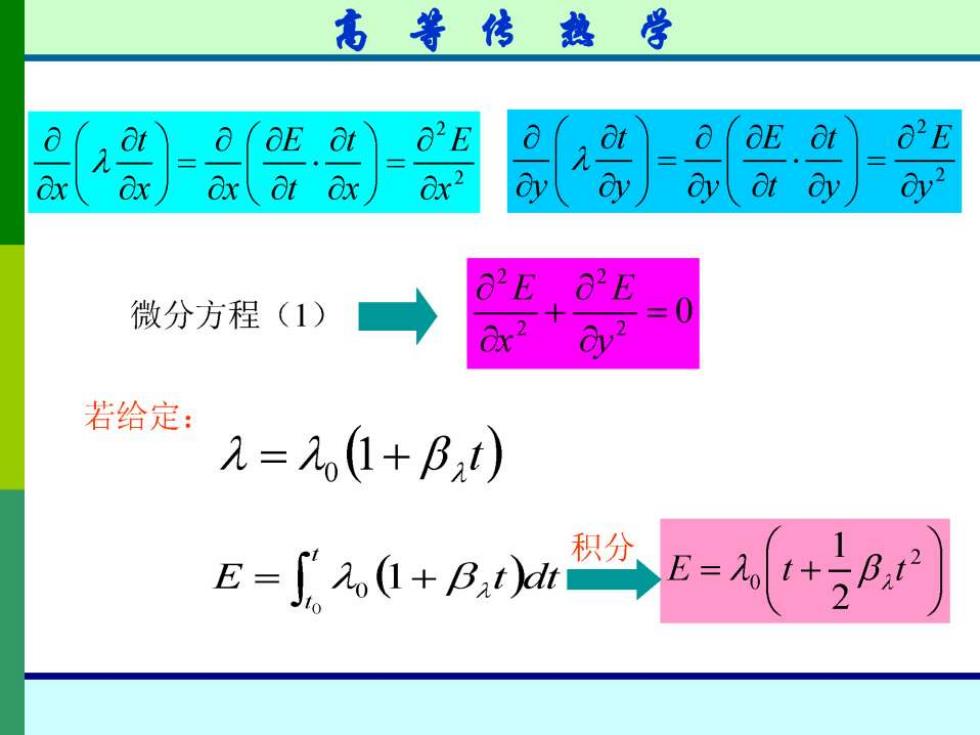
高等传热学 a Ot a OE O2E a OE at 2E 8t Ox ax2 Oy ot ay 微分方程(1) 若给定: 2=2,1+B,) E=+Bat)dr 积分 E=0

高等传热学 三、各向异性体导热 二维、稳态9,=0坐标系取主轴上 微分方程: 是))。 此方程可变为Laplace方程 令: y= 2图 2 元s=Const 元n=Const
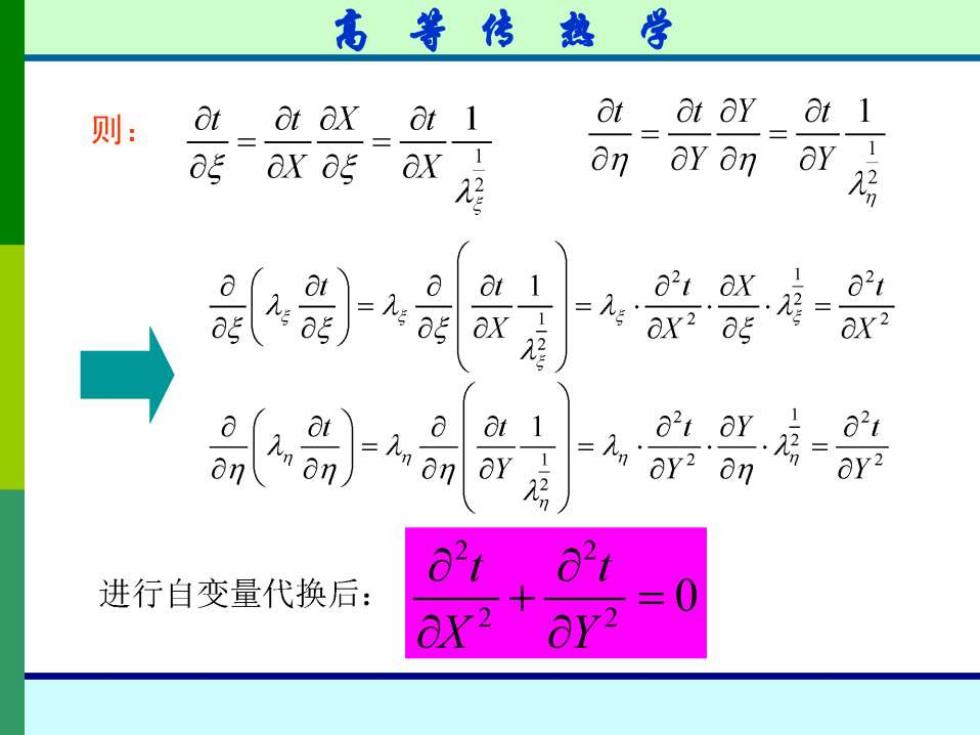
高等传热学 则: Ot at ax at 1 at at ay at 1 og ax ag ax 1 an ay an ay 2 房 a at 1 821 a21 ax ox2 0g ar? a a at 1 821 821 an n an An on oy2 an 进行自变量代换后: ax

高等传热学 四、近似解析法 设: 九=Const;q,均布;tr=Const 引入:0=t-tr b a20a20 微分方程: +9=0 (a) ax20y2 0 边界条件: ∫0-tay=0 (b) 6 9=b=0 (c) IE a0 =0 a 由于对称性x=0时, (d) 0x y=0时, a0 =0 (e) dy