
高等传热学 目录 一、概述 二、集总热容分析 三、大平壁在等温介质中的冷却 四、乘积解 五、非齐次问题 六、定壁温边界条件下半无限大物体的温度响应 七、积分方程近似解 八、常热流边界条件下的半无限大物体
高 等 传 热 学 目 录 一、概述 二、集总热容分析 三、大平壁在等温介质中的冷却 四、乘积解 五、非齐次问题 六、定壁温边界条件下半无限大物体的温度响应 七、积分方程近似解 八、常热流边界条件下的半无限大物体

高等传热学 §1概述 前几章讲了工程上常见的稳定导热过程,它的特点是物体内导热过 程中,温度不随时间发生变化,或者说,物体的内能不发生变化。一般处 于热力设备的稳定或正常工作状态。 工程上同样也有许多的加热或冷却过程中,或热力设备处于启动、 停车或变工况状态,此时物体内温度是随时间变化的不稳定的导热问题。 求解不稳定导热的主要任务是: )确定被加热或冷却物体内部某点达到预定温度所需 的时间。 2)计算物体内部各时刻温度分布随时间变化的速率, 以便核算部件所承受的热应力
高 等 传 热 学
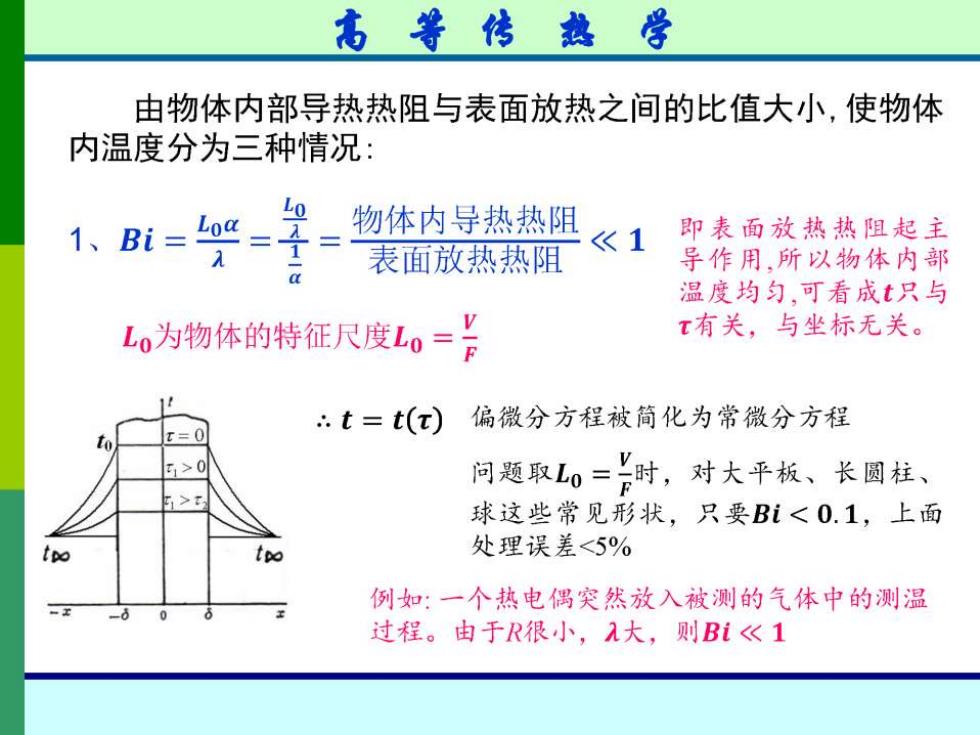
高等传热学 由物体内部导热热阻与表面放热之间的比值大小,使物体 内温度分为三种情况: Lo 1、Bi=0= 物体内导热热阻 T 球这些常见形状,只要Bi<0.1,上面 t po tpo 处理误差<5% 例如:一个热电偶突然放入被测的气体中的测温 过程。由于R很小,1大,则Bi<《1

高等传热学 2、Bi=o》1 一般只要Bi>100即可,导热热阻>放热热阻, 导热热阻起主导作用。所以tw≈t,即表面突 然升高到环境温度,内部温度逐渐变化。 =0 例如:工件在液体中淬火就是此种情况,使第三 类边界条件问题转化成第一类边界条件 因为其内那温度t人位置有关 --6 所以需解偏微分方程 3、Bi=0.1~100之间 r=0 导热热阻与放热热阻是同一数量级,二者对导 热都有影响,都不能忽略。 例如:大工件在空气中冷却或炉内加热过程

高等传热学 §2忽略内部导热热阻(集总热容系统)时 的不稳定导热(Bi<0.1) 一、 环境温度t=Const的情况 1、温度变化规律把物体突然投入与物体温度不同的环境中 设: 物体的表面积为F a,tf 物体的体积为/ a、个p、Cn均为常数 令:0=t-tx, 初始时刻,t=0时,t=t,0=0,=t-ty 由能量守恒方程: aF0 (1) dr

高等传热学 积分并带入初始条件,得: (2) 上式说明物体的过余温度随时间按指数规律减小,π个,日↓ x→00,0=0,t=tr 与环境达到热平衡 2、时间常数 0 无量纲,所以右端 pe V π是无量纲 aF 因此pc,了 具有时间倒数的量纲

高等传热学 如果温度变化进行的时间:?=PC 时, 则: 9=e'=0.368=36.8% 称为时间常数。(C代表冷却到36.8%的时间) 时间常数是这个物体的固有特征,它表示了固有的冷却情 况,即过余温度变化到初始过余温度日的36.8%所需要的时间。 pCp 当 F,则表示达到初始过于温度的36.8%的时间越长, 物体的温度变化越慢,通常称为热惯性越大

高等传热学 测瞬态温度的温度计,必须标出它的时间常数。时间常 数越小,说明对环境温度反映越快,测得的温度越接近真实 温度。 时间常数表示被加热(或冷却)物体,在这个环境下, 冷却(或加热)快慢的标志。 影响时间常数的因素:pC,(物性)c(表面放热系数)片(几何尺度) 如选用测瞬态温度的热电偶,要使时间常数小,则 pCp:尽量小,但受到测温范围热电偶材料特性的限制 0:尽量大,尽量放在流速大的位置 台:尽量小形状,尺寸的影响

高等传热学 三种典型形状的特征尺寸值 F●66 大平板 Lo= 2F 02L 长圆柱 2 球 402 说明:所有条件及r相同的情况下,三种情况时间常数比为6:3:2,大 平板最大,而球最小

高等传热学 应用举例1:动态法测温 ① 已知热电偶的尺寸,即已知:lo或5pcp及mt日 测突然放入被测介质中的t一τ曲线(在未达到最高温度前) aF 由公式(2) 即已知t,T可求tfo t,-t ②因为往往不知道,所以用上式还不行 选用两个热电偶,取不同直径(称双丝法) 2 8_41-t e c 2 12-t -e 0t,-t t-tr :a1=a2=a(直径变化很小1≈2)测出t1~T; t2~T 两条曲线 解两个方程,可求出tr和C