长沙理工大学：《高等传热学》课程电子教案（PPT课件）第八章 湍流流动与传热

高等传热学 目录 一、湍流的物理特性 二、湍流流动的雷诺方程 三、湍流流动的定解问题

高 等 传 热 学 目 录 一、湍流的物理特性 二、湍流流动的雷诺方程 三、湍流流动的定解问题

Re= A 层流 湍流 >小Re >大Re 圆管流动的临界雷诺数： =2100 》流体运动看上 Re=PrD >流体运动 去规则，各部分 看起来极不规 好像是分层流动 则 》质点的迹线或 》脉动与旋涡 流场的流线光滑 >物理理解清楚 >物理理解很 不清楚

层流 ➢ 小Re ➢ 流体运动看上 去规则，各部分 好像是分层流动 ➢ 质点的迹线或 流场的流线光滑 ➢物理理解清楚  vl Re = 湍流 ➢ 大Re ➢ 流体运动 看起来极不规 则 ➢脉动与旋涡 叮叮咚咚等等 ➢物理理解很 不清楚 圆管流动的临界雷诺数： Re = = 2100  vD

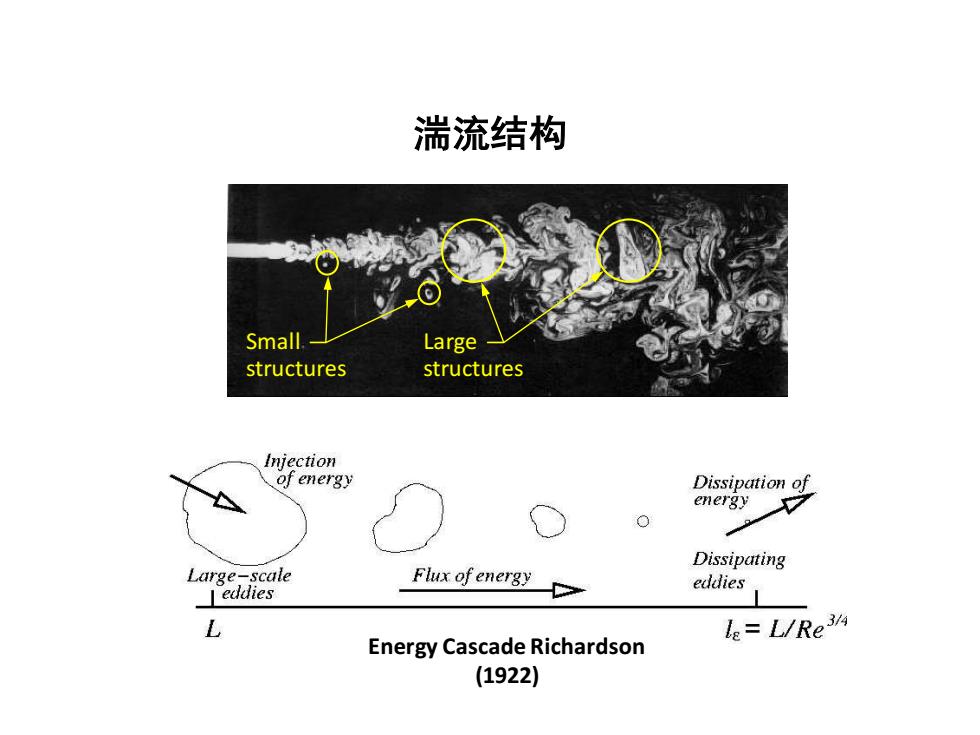
湍流结构 Small. Large structures structures Iniection of energy Dissipation of energy Dissipating Large-scale Ieddies Fiux of energy eddies L le=L/Re3 Energy Cascade Richardson (1922)

湍流结构 Energy Cascade Richardson (1922) Small structures Large structures

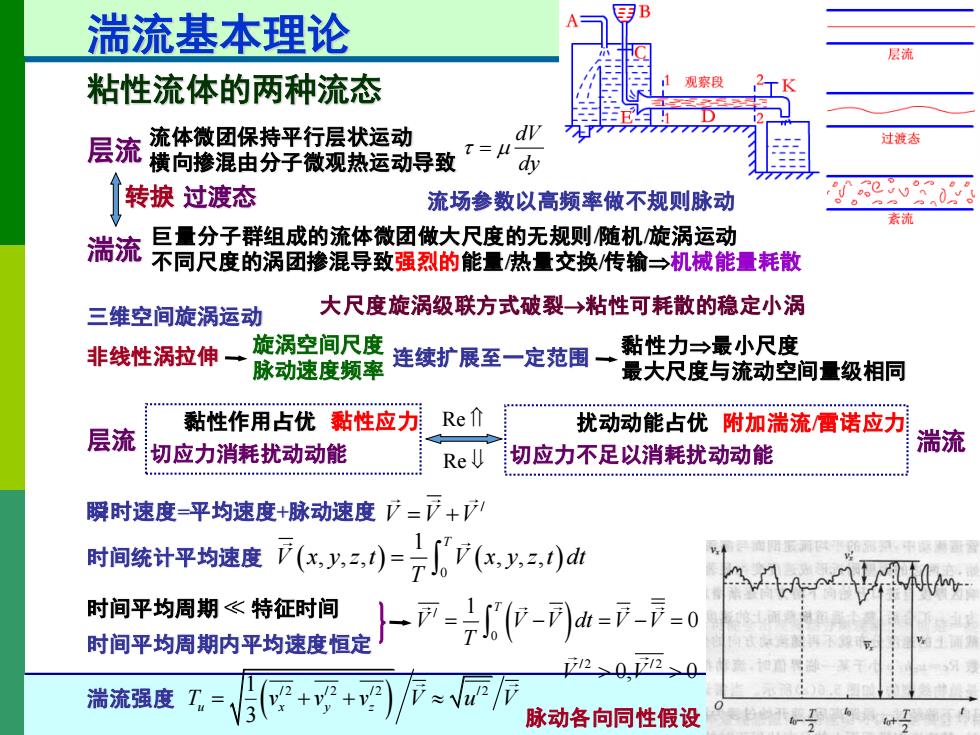
湍流基本理论 层流 粘性流体的两种流态 观察段 层流液德禁冠怪持子曼热爱号致” dy 过渡态 dy 转捩过渡态 0 、60 流场参数以高频率做不规则脉动 紊流 湍流 巨量分子群组成的流体微团做大尺度的无规则随机旋涡运动 不同尺度的涡团摻混导致强烈的能量热量交换传输→机械能量耗散 三维空间旋涡运动 大尺度旋涡级联方式破裂→粘性可耗散的稳定小涡 非线性涡拉伸一 旋涡空间尺度 黏性力一最小尺度 脉动速度频率 连续扩展至一定范围一 最大尺度与流动空间量级相同 黏性作用占优黏性应力 Re 扰动动能占优附加湍流雷诺应力 层流 切应力消耗扰动动能 ReU 切应力不足以消耗扰动动能 湍流 瞬时速度=平均速度+脉动速度广=下+ 时间统计平均速度下(x八，)=r(xy)d 时间平均周期《特征时间 时间平均周期内平均速度恒定 }-=(-=--0 2、0、0 湍流强度T 脉动各向同性假设

5 湍流基本理论 层流 湍流 流体微团保持平行层状运动 横向掺混由分子微观热运动导致 dV dy   = 巨量分子群组成的流体微团做大尺度的无规则/随机/旋涡运动 不同尺度的涡团掺混导致强烈的能量/热量交换/传输机械能量耗散 转捩 过渡态 粘性流体的两种流态 三维空间旋涡运动 非线性涡拉伸 旋涡空间尺度 脉动速度频率 连续扩展至一定范围 黏性力最小尺度 最大尺度与流动空间量级相同 黏性作用占优 切应力消耗扰动动能 层流 Re  Re  扰动动能占优 切应力不足以消耗扰动动能 湍流 黏性应力 附加湍流/雷诺应力 瞬时速度=平均速度+脉动速度 / V V V = + 时间统计平均速度 ( ) ( ) 0 1 , , , , , , T V x y z t V x y z t dt T =  时间平均周期 特征时间 ( ) / 0 1 0 T V V V dt V V T = − = − =  时间平均周期内平均速度恒定 湍流强度 ( ) 1 / 2 / 2 / 2 / 2 3 T v v v V u V u x y z = + +  / 2 / 2 V V   0, 0 脉动各向同性假设 流场参数以高频率做不规则脉动 大尺度旋涡级联方式破裂→粘性可耗散的稳定小涡

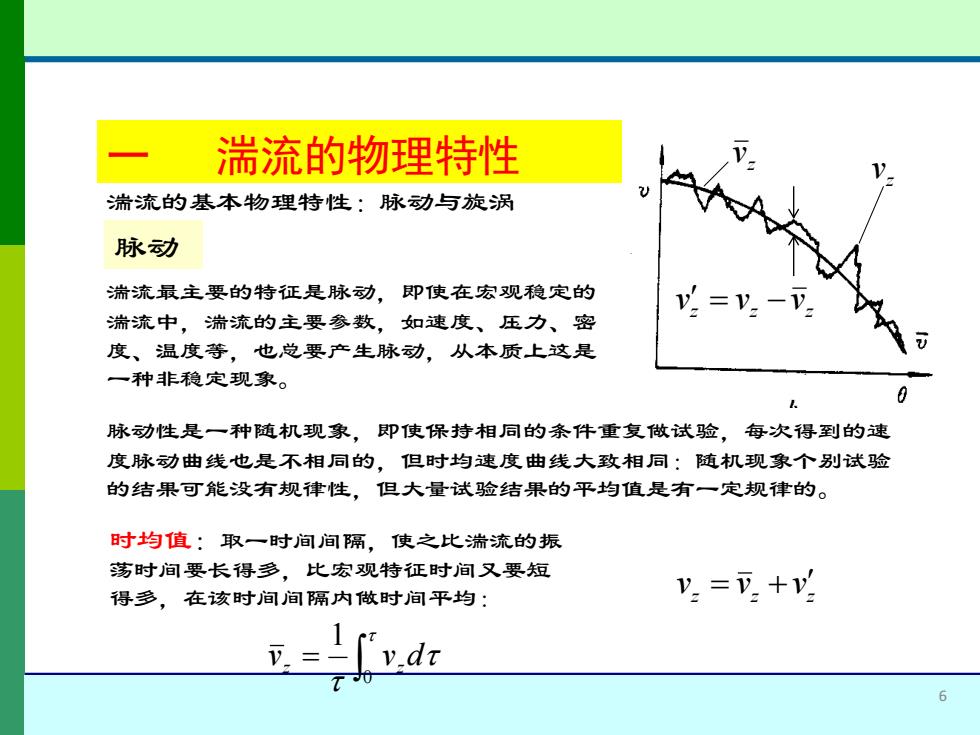
湍流的物理特性 湍流的基本物理特性：脉动与旋涡 脉动 湍流最主要的特征是脉动，即使在宏观稳定的 V.=V.-V. 湍流中，湍流的主要参数，如速度、压力、密 度、温度等，也总要产生脉动，从本质上这是 一种非稳定现象。 0 脉动性是一种随机现象，即使保持相同的条件重复做试验，每次得到的速 度脉动曲线也是不相同的，但时均速度曲线大致相同：随机现象个别试验 的结果可能没有规律性，但大量试验结果的平均值是有一定规律的。 时均值：取一时间间隔，使之比湍流的振 荡时间要长得多，比宏观特征时间又要短 得多， 在该时间间隔内做时间平均： V.=V.+V. v dr 6

6 湍流的基本物理特性：脉动与旋涡 脉动 湍流最主要的特征是脉动，即使在宏观稳定的 湍流中，湍流的主要参数，如速度、压力、密 度、温度等，也总要产生脉动，从本质上这是 一种非稳定现象。 脉动性是一种随机现象，即使保持相同的条件重复做试验，每次得到的速 度脉动曲线也是不相同的，但时均速度曲线大致相同：随机现象个别试验 的结果可能没有规律性，但大量试验结果的平均值是有一定规律的。 z v z v z z z v  = v −v 时均值：取一时间间隔，使之比湍流的振 荡时间要长得多，比宏观特征时间又要短 得多，在该时间间隔内做时间平均：  =    0 1 vz vz d z z z v = v +v  一 湍流的物理特性

湍流的物理特性 旋涡 湍流的另一个特征是旋涡，即流体中存在着的局部迅速旋转的流体 微元，并且这些流体微元处于不断的形成、变化与被破坏过程中。 旋涡的形成： 旋涡的运动： >粘性的作用，速度梯度存在时， >脱离原来的流层 上下流层间的剪切力构成了力矩， 从而可能产生旋涡。 >多个小旋涡合并成大旋涡 >大旋涡分裂成多个小旋涡 》外界作用使流层产生波动。 >旋涡的消失

旋涡 湍流的另一个特征是旋涡，即流体中存在着的局部迅速旋转的流体 微元，并且这些流体微元处于不断的形成、变化与被破坏过程中。 旋涡的形成： ➢ 粘性的作用，速度梯度存在时， 上下流层间的剪切力构成了力矩， 从而可能产生旋涡。 ➢ 外界作用使流层产生波动。 旋涡的运动： ➢ 脱离原来的流层 ➢ 多个小旋涡合并成大旋涡 ➢ 大旋涡分裂成多个小旋涡 ➢ 旋涡的消失 一 湍流的物理特性

湍流流动的雷诺方程 V,=V,+V 口湍流依然受到宏观物理规律的制约，满足连续性方程与 纳维一斯托克斯方程及相应的定解条件。 口湍流运动是一种极不规则的随机运动，脉动频率很高， 从一般给定时间的条件去求解瞬时运动是不可能的。 口从实际应用角度看，某种统计平均值比瞬时值更重要。 雷诺方程：以时均值V。为控制变量 可-r=0 物 dr- :rar-0 理 量 Ov. ax 时均化与偏微分相互独立，表现在数学上，可交换运算次序

❑ 湍流依然受到宏观物理规律的制约，满足连续性方程与 纳维－斯托克斯方程及相应的定解条件。 ❑ 湍流运动是一种极不规则的随机运动，脉动频率很高， 从一般给定时间的条件去求解瞬时运动是不可能的。 ❑ 从实际应用角度看，某种统计平均值比瞬时值更重要。  =    0 1 vz vz d z z z v = v +v  雷诺方程：以时均值 vz 为控制变量 0 1 0  =  =     vz vz d ( ) x v d x v d x v d x v v x vz z z z z z   =    +   =   +  =               0 0 0 1 1 1 时均化与偏微分相互独立，表现在数学上，可交换运算次序。 物 理 量 0 1 1 0 0  =   =    =            v d x d x v x v z z z x v v d x d x v x v z z z z   =   =   =           0 0 1 1 二 湍流流动的雷诺方程

湍流流动的雷诺方程 y:=立+ 时均化与偏微分相互独立， 表现在数学上， 可交换运算次序。 物 i.=-bvdr ov: o2v.o'v. 8x r 0N20 Ox ar2 理 又=var=0 Ov.Ov. 82v. ar2 =0 量 y,=+而，+)=可+可+，+ Vy,=可，+y 凡有带脉动瞬时量的乘积项存在时，就多出一项：单个带脉动的瞬时量 时均化时，相当于把瞬时量换成时均量，对于带脉动瞬时量的乘积顶， 除把瞬时量换成时均量外，还多出一项一一脉动量乘积的时均量

x y x y x y v v = v v + v  v   =    0 1 vz vz d z z z v = v +v  0 1 0  =  =     vz vz d x v x vz z   =   2 2 2 2 x v x vz z   =   = 0    x vz 0 2 2 =    x vz 时均化与偏微分相互独立，表现在数学上，可交换运算次序。 x y x y x y x y x y ( )( v v) = v v + v  v + v v  + v  v  x y x x y y v v = v + v  v + v  物 理 量 凡有带脉动瞬时量的乘积项存在时，就多出一项：单个带脉动的瞬时量 时均化时，相当于把瞬时量换成时均量；对于带脉动瞬时量的乘积项， 除把瞬时量换成时均量外，还多出一项－－脉动量乘积的时均量。 x v x vz z   =   二 湍流流动的雷诺方程

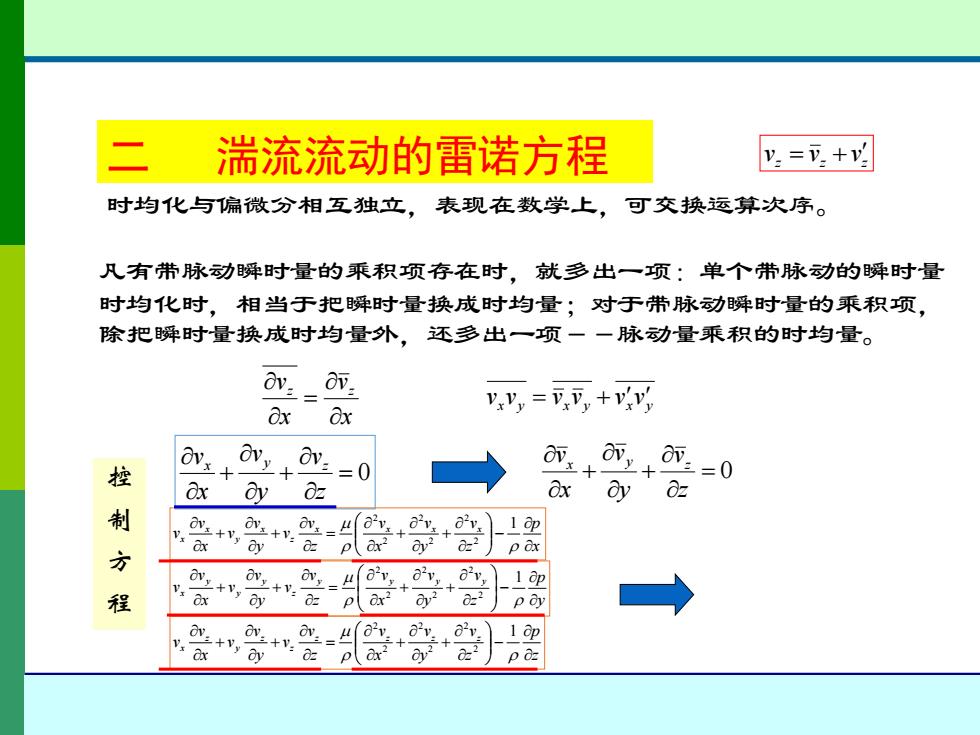
湍流流动的雷诺方程 y=+ 时均化与偏微分相互独立，表现在数学上，可交换运算次序。 凡有带脉动瞬时量的乘积项存在时，就多出一项：单个带脉动的瞬时量 时均化时，相当于把瞬时量换成时均量；对于带脉动瞬时量的乘积项， 除把瞬时量换成时均量外，还多出一项一一脉动量乘积的时均量。 a:_a而 yy,=可，+ 8x Ox 控 0++0=0 ++=0 ax dy 制 +0 1迎 方 r +v, plax dv? v 1 ap +V. 程 p dv ov. ov. 2v + dx 0z 02 p

x y x y x y v v = v v + v  v  z z z v = v +v  时均化与偏微分相互独立，表现在数学上，可交换运算次序。 = 0   +   +   z v y v x vx y z 控 制 方 程 = 0   +   +   z v y v x vx y z x p z v y v x v z v v y v v x v v x x x x z x y x x   −          +   +   =   +   +      1 2 2 2 2 2 2 y p z v y v x v z v v y v v x v v y y y y z y y y x   −           +   +   =   +   +      1 2 2 2 2 2 2 z p z v y v x v z v v y v v x v v z z z z z z y z x   −          +   +   =   +   +      1 2 2 2 2 2 2 凡有带脉动瞬时量的乘积项存在时，就多出一项：单个带脉动的瞬时量 时均化时，相当于把瞬时量换成时均量；对于带脉动瞬时量的乘积项， 除把瞬时量换成时均量外，还多出一项－－脉动量乘积的时均量。 x v x vz z   =   二 湍流流动的雷诺方程

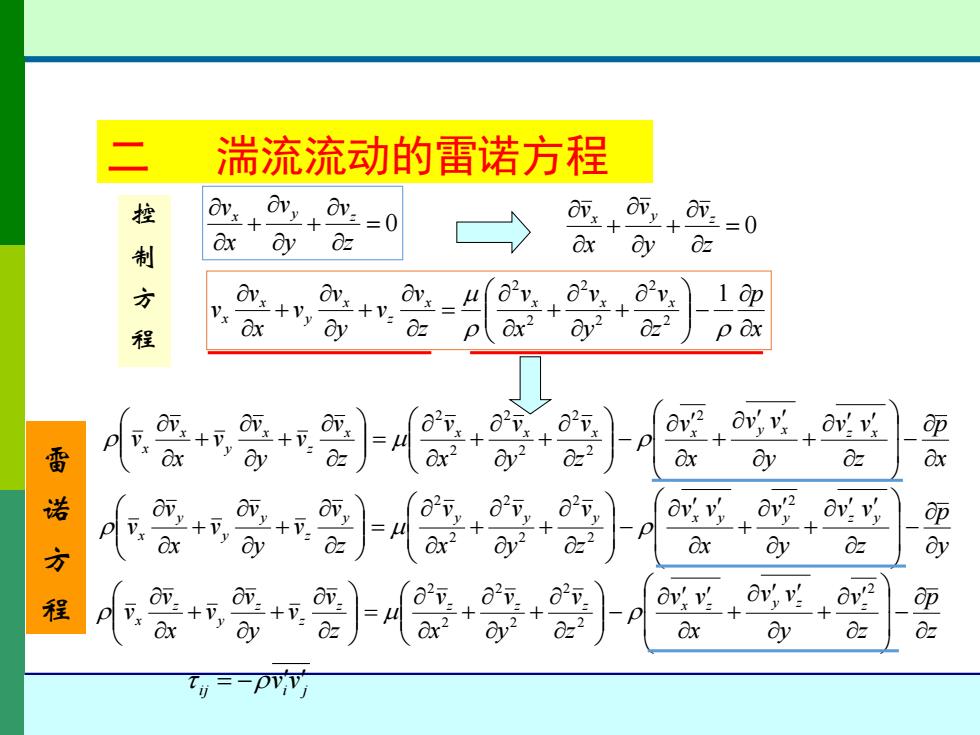
湍流流动的雷诺方程 控 0 丽++0m 制 Ox 0z 二0 8x ay z 方 ov 8v, Vx 1 ap 程 Ox Oy 0z ax2 2 022 pOx OVx+v ov, Ov Ov,v Ov'v, p 匣 番 Ox 0z ☑2 de? Ox y 02 诺 ov.ov. ov,v, v ov.v, +V =u 方 Ox? ☑2 Ox ay 0z 8y 程 2+y 2 o-v ov. Ov,v. av,v Ov'2 匣 z2 Ox Oy Oz

= 0   +   +   z v y v x v 控 x y z 制 方 程 = 0   +   +   z v y v x vx y z x p z v y v x v z v v y v v x v v x x x x z x y x x   −          +   +   =   +   +      1 2 2 2 2 2 2 x p z v v y v v x v z v y v x v z v v y v v x v v x x x x x y x z x z x y x x   −             +     +    −          +   +   =          +   +   2 2 2 2 2 2 2    y p z v v y v x v v z v y v x v z v v y v v x v v y y y y x y y z y z y y y x   −             +    +     −           +   +   =          +   +   2 2 2 2 2 2 2    z p z v y v v x v v z v y v x v z v v y v v x v v z y z z z z z x z z z y z x   −            +     +     −          +   +   =          +   +   2 2 2 2 2 2 2    雷 诺 方 程 ij i j  = −v  v  二 湍流流动的雷诺方程