
高等传热学 第一章导热理论及一维稳态导热 研究目的: 1)确定K,,,) 为选材料、热变形、热应 力的研究提供理论依据 2)确定传热速率q◆ 控制传热 研究思路: 基本物理现象 导热基本定律◆ 建立导热微分方程 单值条件 解析解 求解 数值解 近似解 积分或图解等

高等传热学 §1-1导热及付里叶定律 一、导热 物理现象 宏观:温度不同的各部分物质仅仅由于直接接触, 没有相对运动时,所发生的能量传递现象 微观:微观粒子运动或碰撞的结果 气体一分子碰撞 金属一电子自由运动和原子振动的弹性波 非金属固体一原子振动弹性波 液体、介电质一粒子振动弹性波 关于导热系数的确定:参考“热物性学
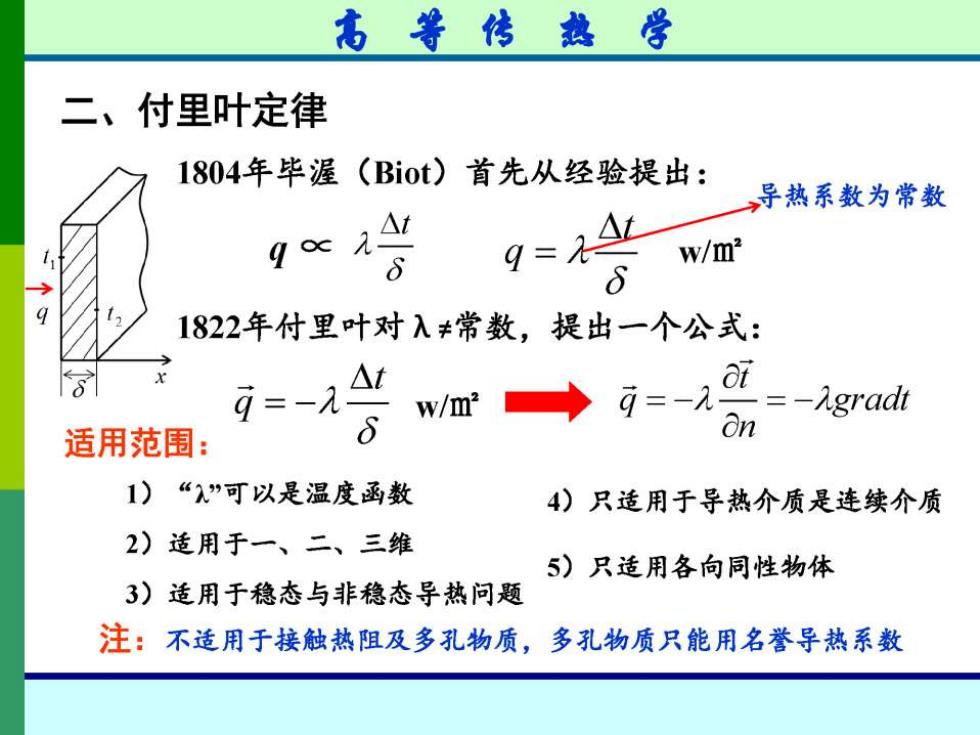
高等传热学 二、付里叶定律 1804年毕渥(Biot)首先从经验提出: ,导热系数为常数 w/m" 8 1822年付里叶对入≠常数,提出一个公式: g=-九 △t a1 w/m g=-=-igradt 适用范围: On 1) “”可以是温度函数 4)只适用于导热介质是连续介质 2)适用于一、二、三维 5)只适用各向同性物体 3)适用于稳态与非稳态导热问题 注:不适用于接触热阻及多孔物质,多孔物质只能用名誉导热系数

高等传热学 三、各向异性材料的导热 各向异性材料:材料导热系数在空间的各个方向上不相同 各向异性材料:晶体材料、木材、石墨、沉积岩、层压的复合材料、由 硅钢片叠加而成的铁心 qx:取决于沿x,y,z三个方向的温度梯度的线性组合 直角坐标系 & -qx=Axx ax +入y影+ +w -9y=1yx0 at Axy Axz q =-Agradt -q2=1zx0 +w +z dt Azy λzz
高 等 传 热 学 三、各向异性材料的导热 各向异性材料:材料导热系数在空间的各个方向上不相同 各向异性材料:晶体材料、木材、石墨、沉积岩、层压的复合材料、由 硅钢片叠加而成的铁心 𝒒𝒙 :取决于沿x,y,z三个方向的温度梯度的线性组合 −𝑞𝑥= 𝜆𝑥𝑥 𝜕𝑡 𝜕𝑥 + 𝜆𝑥𝑦 𝜕𝑡 𝜕𝑦 +𝜆𝑥𝑧 𝜕𝑡 𝜕𝑧 −𝑞𝑦= 𝜆𝑦𝑥 𝜕𝑡 𝜕𝑥 + 𝜆𝑦𝑦 𝜕𝑡 𝜕𝑦 +𝜆𝑦𝑧 𝜕𝑡 𝜕𝑧 −𝑞𝑧 = 𝜆𝑧𝑥 𝜕𝑡 𝜕𝑥 + 𝜆𝑧𝑦 𝜕𝑡 𝜕𝑦 +𝜆𝑧𝑧 𝜕𝑡 𝜕𝑧 直角坐标系 𝒒 = −𝜦𝑔𝑟𝑎𝑑𝑡 𝜦 = 𝜆𝑥𝑥 𝜆𝑥𝑦 𝜆𝑥𝑧 𝜆𝑦𝑥 𝜆𝑦𝑦 𝜆𝑦𝑧 𝜆𝑧𝑥 𝜆𝑧𝑦 𝜆𝑧𝑧
高等传热学 三、各向异性材料的导热 00 图1-10 各向异性材料中的二维导热
高 等 传 热 学 三、各向异性材料的导热
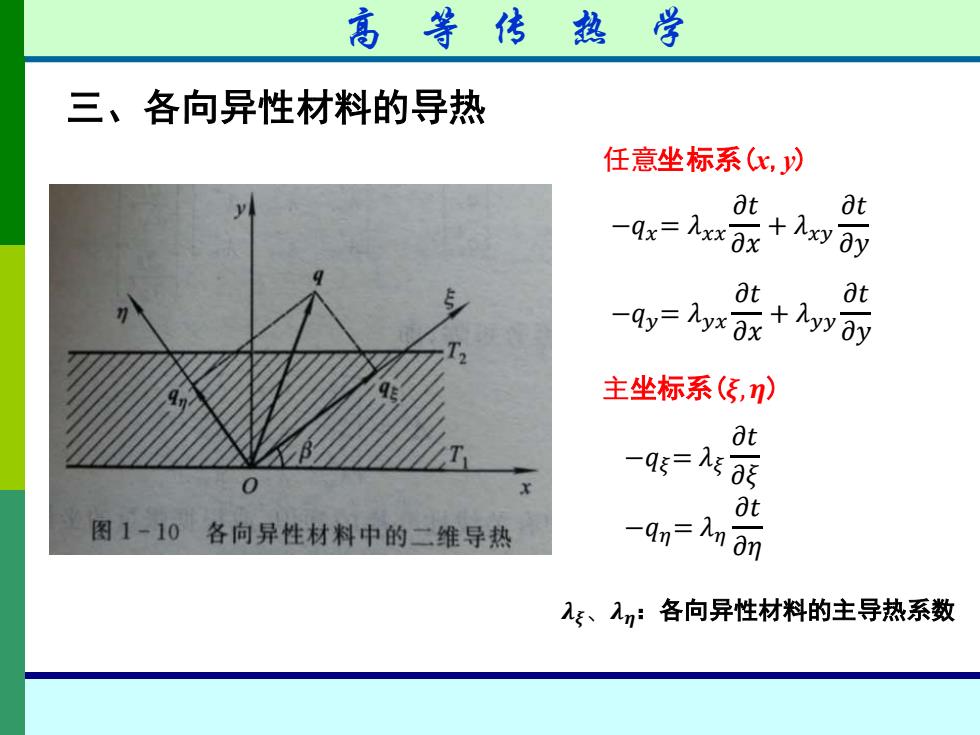
高等传热学 三、各向异性材料的导热 任意坐标系(化,) at Ot -qx=Axx8x +入xy0y O 8t -qy=Ayx 8x .Ayy ay 主坐标系(,) Ot -ag=Ae 图1一10各向异性材料中的二维导热 -an-An On 、入:各向异性材料的主导热系数
三、各向异性材料的导热 −𝑞𝑥= 𝜆𝑥𝑥 𝜕𝑡 𝜕𝑥 + 𝜆𝑥𝑦 𝜕𝑡 𝜕𝑦 −𝑞𝑦= 𝜆𝑦𝑥 𝜕𝑡 𝜕𝑥 + 𝜆𝑦𝑦 𝜕𝑡 𝜕𝑦 任意坐标系(x,y) 主坐标系(𝝃,𝜼) −𝑞𝜉= 𝜆𝜉 𝜕𝑡 𝜕𝜉 −𝑞𝜂= 𝜆𝜂 𝜕𝑡 𝜕𝜂 𝝀𝝃、𝝀𝜼:各向异性材料的主导热系数 高 等 传 热 学

高等传热学 三、各向异性材料的导热 主坐标系(,) 任意坐标系(x,) dt Ot -qx=Axx Ox Ot +Axy dy [8 Axy Ot an =-An on Ot dt 'dy 温度梯度及热流密度与坐标系无关 qx =qcosB-qnsinB (1) 9y=q:sinB+ancosβ(2) at at ax a cosB at sinpβ an (3) at_sinfβ+ ay ag cosB (4) at_cosβ+1 aξax inβ y (5) at_Ot sinβ+ an ax at cosβ y (6)
三、各向异性材料的导热 主坐标系(𝝃,𝜼) 𝑞𝜉 = −𝜆𝜉 𝜕𝑡 𝜕𝜉 𝑞𝜂 = −𝜆𝜂 𝜕𝑡 𝜕𝜂 −𝑞𝑥= 𝜆𝑥𝑥 𝜕𝑡 𝜕𝑥 + 𝜆𝑥𝑦 𝜕𝑡 𝜕𝑦 −𝑞𝑦= 𝜆𝑦𝑥 𝜕𝑡 𝜕𝑥 + 𝜆𝑦𝑦 𝜕𝑡 𝜕𝑦 任意坐标系(x,y) 𝑞𝑥 𝑞𝑦 = − 𝜆𝑥𝑥 𝜆𝑥𝑦 𝜆𝑦𝑥 𝜆𝑦𝑦 𝜕𝑡 𝜕𝑥 𝜕𝑡 𝜕𝑦 温度梯度及热流密度与坐标系无关 𝑞𝑥 = 𝑞𝜉𝑐𝑜𝑠𝛽 − 𝑞𝜂𝑠𝑖𝑛𝛽 𝑞𝑦 = 𝑞𝜉𝑠𝑖𝑛𝛽 + 𝑞𝜂𝑐𝑜𝑠𝛽 𝜕𝑡 𝜕𝑥 = 𝜕𝑡 𝜕𝜉 𝑐𝑜𝑠𝛽 − 𝜕𝑡 𝜕𝜂 𝑠𝑖𝑛𝛽 𝜕𝑡 𝜕𝑦 = 𝜕𝑡 𝜕𝜉 𝑠𝑖𝑛𝛽 + 𝜕𝑡 𝜕𝜂 𝑐𝑜𝑠𝛽 𝜕𝑡 𝜕𝜉 = 𝜕𝑡 𝜕𝑥 𝑐𝑜𝑠𝛽 + 𝜕𝑡 𝜕𝑦 𝑠𝑖𝑛𝛽 𝜕𝑡 𝜕𝜂 =- 𝜕𝑡 𝜕𝑥 𝑠𝑖𝑛𝛽 + 𝜕𝑡 𝜕𝑦 𝑐𝑜𝑠𝛽 (𝟏) (𝟑) (𝟓) (𝟐) (𝟒) (𝟔) 高 等 传 热 学

高等传热学 三、各向异性材料的导热 (5)与(6)代入(1) sinB n))sincos (5)与(6)代入(2) ay=-A)sinBcos-sin+co Axx=1gcos2B+Ansin2B 入xx 入xy at Axy=Ayx =(hg-An)sinBcosB Ayy=hgsin2B+Ancos2B 根据各向异性材料的导热主轴及主轴方向导热系数,求任意方向导热系数
三、各向异性材料的导热 (𝟓)与(6)代入(1) 𝑞𝑥 = −𝜆𝜉 𝜕𝑡 𝜕𝑥 𝑐𝑜𝑠𝛽 + 𝜕𝑡 𝜕𝑦 𝑠𝑖𝑛𝛽 𝑐𝑜𝑠𝛽 + 𝜆𝜂 − 𝜕𝑡 𝜕𝑥 𝑠𝑖𝑛𝛽 + 𝜕𝑡 𝜕𝑦 𝑐𝑜𝑠𝛽 𝑠𝑖𝑛𝛽 = −(𝜆𝜉𝑐𝑜𝑠2𝛽+𝜆𝜂𝑠𝑖𝑛2𝛽) 𝜕𝑡 𝜕𝑥 −(𝜆𝜉 -𝜆𝜂)sin𝛽cos𝛽 𝜕𝑡 𝜕𝑦 (𝟓)与(6)代入(2) 𝑞𝑦 = −(𝜆𝜉−𝜆𝜂)sin𝛽cos𝛽 𝜕𝑡 𝜕𝑥 −(𝜆𝜉𝑠𝑖𝑛2𝛽+𝜆𝜂𝑐𝑜𝑠2𝛽) 𝜕𝑡 𝜕𝑦 𝑞𝑥 𝑞𝑦 = − 𝜆𝑥𝑥 𝜆𝑥𝑦 𝜆𝑦𝑥 𝜆𝑦𝑦 𝜕𝑡 𝜕𝑥 𝜕𝑡 𝜕𝑦 𝜆𝑥𝑥=𝜆𝜉𝑐𝑜𝑠2𝛽 + 𝜆𝜂𝑠𝑖𝑛2𝛽 𝜆𝑥𝑦=𝜆𝑦𝑥 = 𝜆𝜉 − 𝜆𝜂 𝑠𝑖𝑛𝛽𝑐𝑜𝑠𝛽 𝜆𝑦𝑦=𝜆𝜉𝑠𝑖𝑛2𝛽 + 𝜆𝜂𝑐𝑜𝑠2𝛽 根据各向异性材料的导热主轴及主轴方向导热系数,求任意方向导热系数 高 等 传 热 学

高等传热学 三、各向异性材料的导热 直角坐标系 pe架-民as2a+amA8装+cm8+as9+ at 2gr,kos8snB。 坐标系与各向异性材料热导率的主轴相一致 ∂t. ∂2t. 02t 圆柱坐标系:坐标系与各向异性材料热导率的主轴相一致 82t pc ot aroot aop02t at r arar
三、各向异性材料的导热 直角坐标系 𝜌𝑐 𝜕𝑡 𝜕𝜏 = 𝜆𝜉𝑐𝑜𝑠2𝛽 + 𝜆𝜂𝑠𝑖𝑛2𝛽 𝜕 2 𝑡 𝜕𝑥 2 + 𝜆𝜉𝑠𝑖𝑛2𝛽 + 𝜆𝜂𝑐𝑜𝑠2𝛽 𝜕 2 𝑡 𝜕𝑦 2 + 2(𝜆𝜉 -𝜆𝜂)cos𝛽sin𝛽 𝜕 2𝑡 𝜕𝑥𝜕𝑦 +𝑞𝑣 高 等 传 热 学 坐标系与各向异性材料热导率的主轴相一致 𝜌𝑐 𝜕𝑡 𝜕𝜏 = 𝜆𝑟 𝑟 𝜕 𝜕𝑟 𝑟 𝜕𝑡 𝜕𝑟 + 𝜆𝜑 𝑟 2 𝜕 2 𝑡 𝜕𝜑2 + 𝜆𝑍 𝜕 2 𝑡 𝜕𝑧 2 圆柱坐标系:坐标系与各向异性材料热导率的主轴相一致 𝜌𝑐 𝜕𝑡 𝜕𝜏 = 𝜆𝜉 𝜕 2 𝑡 𝜕𝑥 2 + 𝜆𝜂 𝜕 2 𝑡 𝜕𝑦 2 + 𝑞𝑣

高等传热学 §2导热微分方程 一 导热微分方程的建立 各向同性体:9=-入 ∂ti On 各向异性体取坐标主轴上: 可=-元,6x a- Ot 0z 1.直角坐标 qz+O z dz dxdy qydxdz 1)取微元体 qxdydz dx 9x+ aqx dx dydz 9y+ dxdz q-dxdy