
D0:10.16285j.rsm.2011.s1.034 文章墙号:1000-7598(20111增刊1一0309-05 土体一维冻结问题温度场半解析解 周扬,周国庆 (1.中国矿业大学深都岩士力学与地下工程国家重点实验室,江苏徐州208:2中国矿业大学力学与建筑工程学院。江苏徐州26) 摘要:针对土体的一维冻结过程,采用考虑土体冻结状态下未冻水存在的等效热容模型,建立了其温度场计算的半解析方 法,并与相关文献中的数值解进行了对比,验证了方法的正确性。对等效热容模型与显热容模型进行了对比,计算结果表明: 在腾态阶段,显热容模型计算的冻结锋面推进速度较等效热容模型慢:而在接近稳态阶段,显热容模型计算的冻土区厚度较 等效热容模型厚。在冻结诱导水流较弱的情形下,土体冻结状态下的持水特性越好,采用显热容模型进行温度场计算产生的 误差越显著,并且其计算结果应用于人工冻结设计是偏于不安全的。 关使词:土壤冻结:温度场:半解析解,等效热容模型:显热容模型:未冻水 中图分类号:TU2 文献标识码:A Semi-analytical solution for temperature field of one-dimensional soil freezing problem ZHOU Yang.ZHOU Guo-qing Abstraet:In order to calculate the temperature of the one-dimensionl soil freezing process.the equivalent heat capacity model which considers the nfrz water con has been applied and the semi-analytical solutiofor the temperature field has been obtained.Thesolution procedure has been based ontheFourier method,and the solution has beenonfed by comparing with the numerical solution in some references.The comparison between the equivalent heat capacity model and the apparent heat capacity model has been made,and the resu indicate that,during the transistage,the advancing velocity of the freezing front calculated rom the apparent heat capacity model is smaller than that of the quivalent heat capacity model,during the steady stage.the ckness of the frozen zone calculated from the apparent heat capacity model is larger than that of the equivalent heat capacity mode on that the water model is used to calculate the temperature f arger the error gets ate the temperature field,and the results are unsafe 1引言 对于温度场的计算模型,最完善的是综合考虑 温度场、水分场、应力场等耦合作用的模型,如刚 无论是寒区工程还是冻结法施工均不可避免 性冰模型、水-热-力耦合模型等,这些模型一般 地遇到土壤的冻结,土壤冻结过程中温度场的计算 不适合用于工程计算。常用于工程计算的模型是显 具有重要的意义 是 工地层冻结技术 论研究的 热容模型,该模型将土体的冻结视为 般的相变 基础,同时也是运用冻结法进行设计与施工的主要 导热过程,许多商业软件计算土壤冻结温度场均是 依据四。 基于该模型。 学整金重点项目(o5053400):国家白然科学基金面上项目(No.4071021)国家科技计划重点项目(0.2006BAB16B01 1994-2016 China Academie Journal Eleetronic Publishing House.All rights reserved. http://www.cnki.ne
第 32 卷增刊 1 岩 土 力 学 Vol.32 Supp.1 2011 年 4 月 Rock and Soil Mechanics Apr. 2011 收稿日期:2010-11-04 基金项目:国家自然科学基金重点项目(No. 50534040);国家自然科学基金面上项目(No. 40471021);国家科技计划重点项目(No. 2006BAB16B01); 中国矿业大学青年科研基金(No. 2009A007)。 第一作者简介:周扬,男,1982 年生,博士,讲师,主要从事冻土物理学方面的研究。E-mail:tod2006@126.com 文章编号:1000-7598 (2011)增刊 1-0309-05 土体一维冻结问题温度场半解析解 周 扬,周国庆 (1. 中国矿业大学 深部岩土力学与地下工程国家重点实验室,江苏 徐州 221008;2. 中国矿业大学 力学与建筑工程学院,江苏 徐州 221116) 摘 要:针对土体的一维冻结过程,采用考虑土体冻结状态下未冻水存在的等效热容模型,建立了其温度场计算的半解析方 法, 并与相关文献中的数值解进行了对比,验证了方法的正确性。对等效热容模型与显热容模型进行了对比, 计算结果表明: 在瞬态阶段,显热容模型计算的冻结锋面推进速度较等效热容模型慢;而在接近稳态阶段,显热容模型计算的冻土区厚度较 等效热容模型厚。在冻结诱导水流较弱的情形下,土体冻结状态下的持水特性越好,采用显热容模型进行温度场计算产生的 误差越显著,并且其计算结果应用于人工冻结设计是偏于不安全的。 关 键 词:土壤冻结;温度场;半解析解; 等效热容模型;显热容模型;未冻水 中图分类号:TU 2 文献标识码:A Semi-analytical solution for temperature field of one-dimensional soil freezing problem ZHOU Yang, ZHOU Guo-qing (1. State Key Laboratory for Geomechanics and Deep Underground Engineering, China University of Mining & Technology, Xuzhou, Jiangsu 221008, China; 2. School of Mechanics & Civil Engineering, China University of Mining & Technology, Xuzhou, Jiangsu 221116, China) Abstract: In order to calculate the temperature of the one-dimensional soil freezing process, the equivalent heat capacity model which considers the unfrozen water content has been applied; and the semi-analytical solution for the temperature field has been obtained. The solution procedure has been based on the Fourier method, and the solution has been confirmed by comparing with the numerical solution in some references. The comparison between the equivalent heat capacity model and the apparent heat capacity model has been made; and the results indicate that, during the transient stage, the advancing velocity of the freezing front calculated from the apparent heat capacity model is smaller than that of the equivalent heat capacity model; during the steady stage, the thickness of the frozen zone calculated from the apparent heat capacity model is larger than that of the equivalent heat capacity model. Considering the situation that the water flow induced by the freezing process is weak, then the better the soil freezing characteristic is, the larger the error gets when the apparent heat capacity model is used to calculate the temperature field; and the results are unsafe for the design of the artificial ground freezing engineering. Key words: soil freezing; temperature field; semi-analytical solution; equivalent heat capacity model; apparent heat capacity model; unfrozen water 1 引 言 无论是寒区工程还是冻结法施工均不可避免 地遇到土壤的冻结,土壤冻结过程中温度场的计算 具有重要的意义,是人工地层冻结技术理论研究的 基础,同时也是运用冻结法进行设计与施工的主要 依据[1]。 对于温度场的计算模型,最完善的是综合考虑 温度场、水分场、应力场等耦合作用的模型,如刚 性冰模型[2]、水-热-力耦合模型[3]等,这些模型一般 不适合用于工程计算。常用于工程计算的模型是显 热容模型[4],该模型将土体的冻结视为一般的相变 导热过程,许多商业软件计算土壤冻结温度场均是 基于该模型。 DOI:10.16285/j.rsm.2011.s1.034

310 岩 力 学 2011年 然而,十体风别于传梦相变导执村程的一个品 木文将参考文献「11-14]中用于求解线性因结问 著特征是在冻结状态下会存在一定数量的未冻水, 题的方法获得其半解析解,基本的思想可以表述如 这是显热容棋型所没有考虑的。文献5]中通过对才 下:对该过程在空间上和时间上进行分段,将士体 热耦合模型的简化,得到了形式简单的等效热容模 划分为n层,每一层标记为,其厚度为h:同时 型。该模型考虑了十体的冻结特性曲线(即未冻水 将十体的冻结时程在时间上也制分为是够小的冬个 含量与负温的关系),基本适用于土体中冻结诱导水 时段,用符号k来表示其中的某一时段,。 流较弱条件下的温度场计算问题。 每一薄层在时段k内的参数随空间和时间的 本文 维冻结过程, 采用等效热容 变化都较微小,因此,可以近似取:时刻的平均 模型进行温度场计算,建立一种半解析分析方法, 值作为薄层在时段k内的相应值,这样在每一个 并进行相关的算例讨论。 时段k内土体经历的过程可以视为层状土体的导热 2基本方程及条件 问题, 如图1所示。 文献5)给出了土壤冻结过程温度场计算的等 效热容模型,其基本方程如下: (1) 式中:C,为等效热容,在未冻土段即为体积热容 C,而在冻土段则为C.+Lp0./T,L为相变 潜热,P.为水的密度,日,为未冻水体积含量:元为 土体导热系数。 3.2k时段的求解 =4-T)8 (2) 通过31节对模型分层线性化后,k时段内的层 式中:参数A、B与士性有关。 状土体导热问题的基本方程为 土体的体积热容C,可由下式计算-: ,=1.2.3n (5) C,=C6.+C8+C,8+C8. (3) 式中:日、日、日分别为冰、土颗粒、空气体积含 式中:a=a/C,为1时刻2在i层上的平 量:Cm、C、C,、C,分别为水、冰、土骨架、空 均值,=∫(,4)d:/h,Cw为1时刻C,在 气的热容。 土导热系数可以用几何平均公式表示-] 1层上的平均值,Cv.=[C(e,-)d:1h。 入=元元"入4入% (4) 土体两端的温度边界条件为 7=7.二=0=0 式中:元、无、入、入分别为水、冰、土骨架、 (6) 空气的导热系数。 T=T,E=8.=H 考虑一段土体,其厚度为H,初始时刻温度分 在土层交界面:=处,需要满足如下条件: 布任意,土体经历由上而下冻结,上端部为冷端, (7) 温度恒定为T:下端部为暖端,温度恒定为T。与 此单值性条件相应的工程背景如文献9中的地层 e) 初始条件即为,时刻的温度场分布 冬季冻结,此时T:为冬季地表平均温度,H为温度 Ta=T(),l,2,3,n(8) 场影响深度:文献10中的土体室内连续冻结试验 也符合此单值性条件。 下面对该层状土体导热问题进行求解,首先要 进行边界条件齐次化,令 3问题的求解 T=T0+T2,l,2,3,n(9) 3.1基本思想 其中T)是满足基本方程及边界、土层交界面 对于非线性方程式(1),无法求得其解析解, 条件的一组特解,容易给出如下一组: 1002016Ci Academie al Electronic Publishing House.All rights eserved http://www.cnki.ne
310 岩 土 力 学 2011 年 然而,土体区别于传统相变导热过程的一个显 著特征是在冻结状态下会存在一定数量的未冻水, 这是显热容模型所没有考虑的。文献[5]中通过对水 热耦合模型的简化,得到了形式简单的等效热容模 型,该模型考虑了土体的冻结特性曲线(即未冻水 含量与负温的关系),基本适用于土体中冻结诱导水 流较弱条件下的温度场计算问题。 本文针对土壤的一维冻结过程,采用等效热容 模型进行温度场计算,建立一种半解析分析方法, 并进行相关的算例讨论。 2 基本方程及条件 文献[5]给出了土壤冻结过程温度场计算的等 效热容模型,其基本方程如下: v ( ) T T C txx λ ∂ ∂∂ = ∂∂ ∂ (1) 式中: Cv 为等效热容,在未冻土段即为体积热容 Cv ,而在冻土段则为 v wu CL T + ∂∂ ρ θ / ,L 为相变 潜热,ρ w 为水的密度,θu 为未冻水体积含量;λ 为 土体导热系数。 土壤的冻结特性即未冻水与负温的关系可表 示为[6] u ( ) B θ A T − = − (2) 式中:参数 A、B 与土性有关。 土体的体积热容Cv 可由下式计算[7–8]: CC C C C v wu ii ss aa = ++ + θ θθ θ (3) 式中:θi 、θs 、θa 分别为冰、土颗粒、空气体积含 量;Cw 、Ci 、Cs 、Ca 分别为水、冰、土骨架、空 气的热容。 土壤导热系数可以用几何平均公式表示[7–8] u sa i w isa θ θ θ θ λ = λ λλλ (4) 式中: λw 、 λi 、 λs 、 λa 分别为水、冰、土骨架、 空气的导热系数。 考虑一段土体,其厚度为 H,初始时刻温度分 布任意,土体经历由上而下冻结,上端部为冷端, 温度恒定为 Tc;下端部为暖端,温度恒定为 Tw。与 此单值性条件相应的工程背景如文献[9]中的地层 冬季冻结,此时 Tc为冬季地表平均温度,H 为温度 场影响深度;文献[10]中的土体室内连续冻结试验 也符合此单值性条件。 3 问题的求解 3.1 基本思想 对于非线性方程式(1),无法求得其解析解, 本文将参考文献[11–14]中用于求解非线性固结问 题的方法获得其半解析解,基本的思想可以表述如 下:对该过程在空间上和时间上进行分段,将土体 划分为 n 层,每一层标记为 i,其厚度为 hi;同时, 将土体的冻结过程在时间上也划分为足够小的各个 时段,用符号 k 来表示其中的某一时段[tk-1,tk]。 每一薄层 i 在时段 k 内的参数随空间和时间的 变化都较微小,因此,可以近似取 tk-1 时刻的平均 值作为薄层 i 在时段 k 内的相应值,这样在每一个 时段 k 内土体经历的过程可以视为层状土体的导热 问题,如图 1 所示。 图 1 分层示意图 Fig.1 The divided soil layers 3.2 k 时段的求解 通过 3.1 节对模型分层线性化后,k 时段内的层 状土体导热问题的基本方程为 2 2 i i ik T T a t z ∂ ∂ = ∂ ∂ , i=1, 2, 3,…, n (5) 式中: v / ik ik ik a C = λ ,λik 为 tk-1 时刻λ 在 i 层上的平 均值, 1 1 ( , )d / i i z ik k i z λ λ zt z h − = ∫ − ,Cvik 为 tk-1时刻Cv 在 i 层上的平均值, 1 V 1 ( , )d / i i z ik v k i z C C zt z h − = ∫ − 。 土体两端的温度边界条件为 c 0 w , 0 , n TTzz TT zz H = == ⎫ ⎬ = == ⎭ (6) 在土层交界面 i z z = 处,需要满足如下条件: 1 ( 1) 1 / / i i ik i i k i T T λ λ Tz T z + + + = ⎫⎪ ⎬ ∂ ∂= ∂ ∂ ⎪⎭ (7) 初始条件即为 tk-1时刻的温度场分布 1 ,initial , ( ) k T Tz i it − = ,i=1, 2, 3, …, n (8) 下面对该层状土体导热问题进行求解,首先要 进行边界条件齐次化,令 (1) (2) Ti = Ti +Ti , i=1, 2, 3,…, n (9) 其中 (2) Ti 是满足基本方程及边界、土层交界面 条件的一组特解,容易给出如下一组:

增刊1 周扬等:土体一维冻结问蔻温度场半解析解 311 ,1,2,…,n(10) B。=6au1H (25) (26 式中:T、T分别为、处的温度,由下式计算: 8日=m46骨+Bco46 工=收-会老 (11) 对于系数A、B,需要满足下列递推公式 [【A,BJ'=[41,0j (27) 不-7+收-务 (12) [【4m,B'=S[4-,B-nJ,i=2,3.…,n(28) 式(27)由0处齐次边界条件获得,式(28)由1 式(9)中T"则满足基本方程与齐次边界条件, m1处的层间接触条件获得。 其初始条件为 递推矩阵S,=CD,其中 I= T.e)-T(e)=T(e),12,,n(13) 于"的定解问题,可采用分离变量法进行 cos4.治)-sin(4. 求解。令 T0=Z.(=)R),=12.….n(14) D 代入式(5)后变形得到 d.cos)-d,sin() a,R()Z.() (15) 上式成立则必同等于一个常数,记为a,则有 由式(27)~(28)可知,所有的系数A、B R'0-a,a.R0=0 (16) 都包含同样的因子A,于是可以把它提取出来, Z1)-aZ,(e)=0 (17) 则式(24)变化为 由式(16)的解答及实际问题的性质知a非正 于是可设 T"=248eew,l,2,3,…,n(29 =- (18) 此时式(27)中的A则变为1,新的系数A, 则式(16)、(17)的通解分别为 B由递推关系完全确定。 R.(1)= (19) 由处的边界条件可以得到特征值序列.的 Z,(=)=4 sin(n=)+B,cos(n=) 特征方程如下: (20) SSS,…S,S=0 (30) 因为m可以为不同的序列,因此,可得到式(5) 的通解为 其中,S,…,Sn在前面已有定义,另有 S=1,0 T=14.sin(n)+B cos(ne(1) S=[sin().cos( 式中:A、B为系数。因为层间条件式(7),n 利用初始条件,可以建立方程如下: 的选择需需要使各层T”随:的变化具有相同的形 式,序列6满足式(22) 248.e=e,23.n(G31 2au/H=2a,=l,2,3,…(22) 特征函数g(e)满足正交关系吲 n=6n4/H,m=l,2,3… (23 ∑Cu8neg(e)d:=0,,当m≠n时 利用该正交关系及初始条件可以获得A T"-∑8e)e则,l,2,3.,n(24) 4.八元eaea (32) 其中 cdz 99-016 China Academic Joumal Electronic Publishing House.All rights reserved.htp:/www
增刊 1 周 扬等:土体一维冻结问题温度场半解析解 311 (2) 1 1 1 i i ia b ii ii z z zz TT T zz zz − − − − − = + − − ,i=1, 2, …, n (10) 式中:Ta 、Tb 分别为 zi-1、zi处的温度,由下式计算: 1 c wc 1 1 ( ) /( ) i n j j a j j jk jk h h TT TT λ λ − = = =+ − ∑ ∑ (11) c wc 1 1 ( ) /( ) i n j j b j j jk jk h h TT TT = = λ λ =+ − ∑ ∑ (12) 式(9)中 (1) Ti 则满足基本方程与齐次边界条件, 其初始条件为 (1) ,initial( ) T z i = 1 , 1 (2) , () () () k itk T zT zT z it i − − ∗ − = , i=1,2,…, n (13) 对于 (1) Ti 的定解问题,可采用分离变量法进行 求解。令 (1) ( ) () T Z zR t i ii = ,i=1,2,…, n (14) 代入式(5)后变形得到 () ( ) () ( ) i i ik i i Rt Z z aRt Z z ′ ′′ = (15) 上式成立则必同等于一个常数,记为αi ,则有 () () 0 Rt aRt i i ik i ′ − = α (16) () () 0 Zz Zz i ii ′′ − = α (17) 由式(16)的解答及实际问题的性质知αi 非正, 于是可设 2 αi i = −η (18) 则式(16)、(17)的通解分别为 2 () e i ik a t R t i −η = (19) ( ) sin( ) cos( ) Zi ii i i zA zB z = + η η (20) 因为ηi 可以为不同的序列,因此,可得到式(5) 的通解为 2 (1) 1 [ sin( ) cos( )]e mi ik a t i mi mi mi mi m T A zB z η η η ∞ − = = + ∑ (21) 式中:Ami 、Bmi 为系数。因为层间条件式(7),η mi 的选择需需要使各层 (1) Ti 随 t 的变化具有相同的形 式,序列 m ε 满足式(22), 2 22 1 / m k mi ik ε η aH a = ,m=1, 2, 3, … (22) 即 / η εµ mi m i = H ,m=1, 2, 3, … (23) 式中: 1 / i k ik µ = a a 。 于是通解形式变化为 (1) 1 ( )e mt i mi m T gz β ∞ − = = ∑ ,i=1, 2, 3, …, n (24) 其中 2 2 1 / m mk β ε = a H (25) ( ) sin( ) cos( ) mi mi i m mi i m z z gz A B H H = + µε µε (26) 对于系数 Ami 、 Bmi ,需要满足下列递推公式: T T 11 1 [ , ] [ ,0] AB A mm m = (27) T [,] A B mi mi = T ( 1) ( 1) [,] Si mi mi A B − − , i=2, 3, …, n(28) 式(27)由 z0处齐次边界条件获得,式(28)由 z1 ~ zn-1处的层间接触条件获得。 递推矩阵 Si ii = C D ,其中 1 1 1 1 sin( ) cos( ) cos( ) sin( ) i i im im i i i im im z z H H z z H H µε µε µε µε − − − − ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ − ⎢ ⎥ ⎣ ⎦ C 1 1 1 1 1 1 1 1 sin( ) cos( ) cos( ) sin( ) i i im im i i i i im i im z z H H z z d d H H µε µε µε µε − − − − − − − − ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ − ⎢ ⎥ ⎣ ⎦ D ( 1) ( 1) i k ik i ik i k a d a λ λ − − = 由式(27)~(28)可知,所有的系数 Ami 、Bmi 都包含同样的因子 Ami ,于是可以把它提取出来, 则式(24)变化为 (1) 1 1 ( )e mt i m mi m T Ag z β ∞ − = = ∑ ,i=1, 2, 3,…, n (29) 此时式(27)中的 Am1则变为 1,新的系数 Ami , Bmi 由递推关系完全确定。 由 zn 处的边界条件可以得到特征值序列 m ε 的 特征方程如下: 1 1 21 0 S SS SS n nn + − " = (30) 其中 S2,S3,…,Sn在前面已有定义,另有 T 1 S = [1,0] 1 [sin( ),cos( )] n nm nm µ ε µε S + = 利用初始条件,可以建立方程如下: 1 1 , 1 () () m mi i tk m A gz T z − ∞ ∗ = ∑ = , i=1, 2, 3, …, n (31) 特征函数 ( ) mi g z 满足正交关系[15] 1 v 1 ( ) ( )d 0 i i n z ik mi ni z i C g zg z z − = ∑ = ∫ ,当m ≠ n 时。 利用该正交关系及初始条件可以获得 Am1 1 1 1 v , 1 1 2 v 1 ( ) ( )d ( )d i k i i i n z ik i t mi z i m n z ik mi z i C T zg z z A C gzz − − − ∗ = = = ∑ ∫ ∑ ∫ (32)
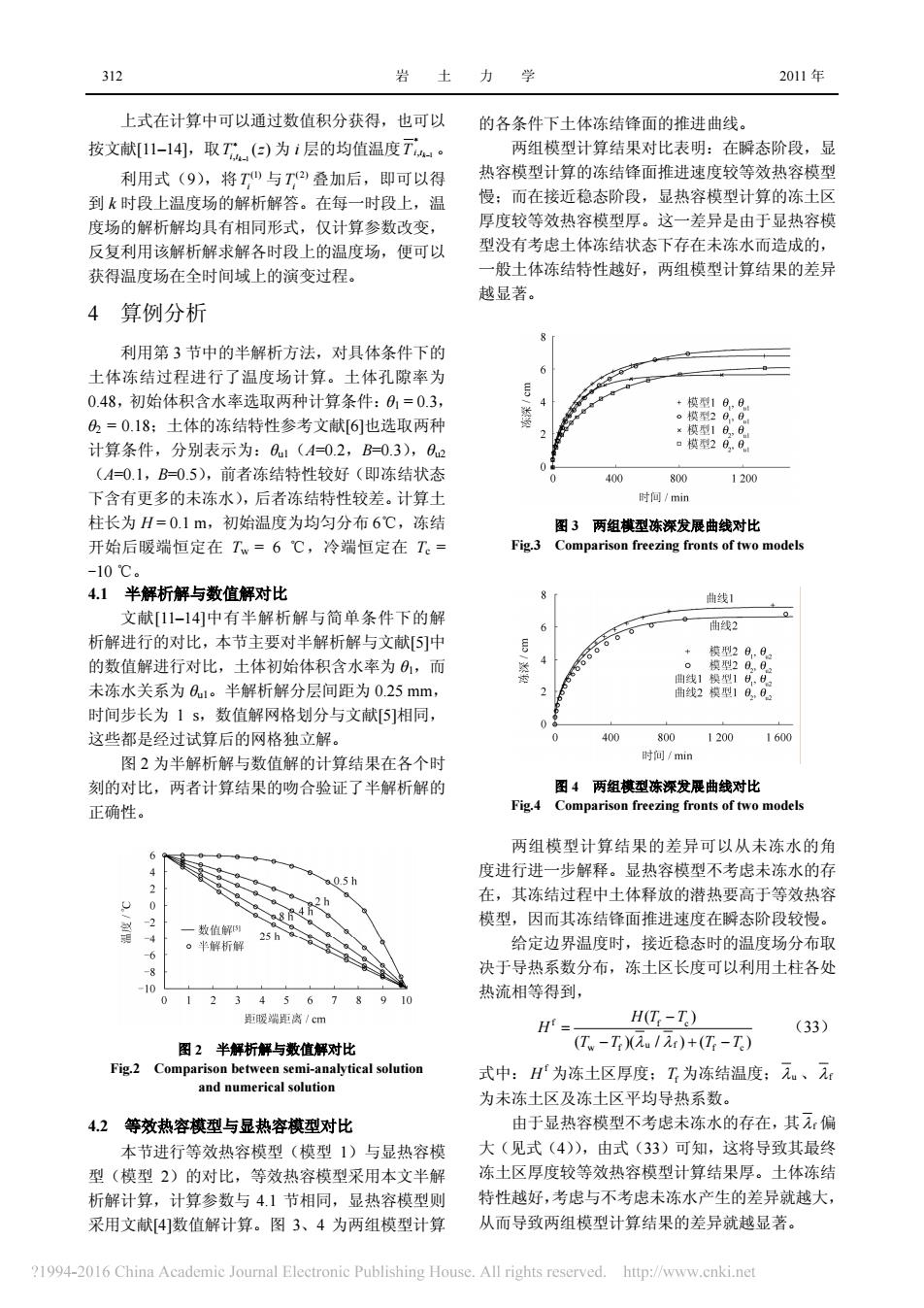
312 力 学 2011年 上式在计算中可以通过数值积分获得,也可以 的各条件下土体冻结锋面的推进曲线。 按文献l-l4,取T()为i层的均值温度TM: 两组模型计算结果对比表明:在瞬态阶段,显 利用式(9),将T与T)叠加后,即可以得 热容模型计算的冻结锋面推进速度较等效热容模型 到k时段上温度场的解析解答。在每一时段上,温 慢 而在接近稳态阶段 显热容模型计算的冻士区 府场的解折解均且有相同形式,仅计算参数改亦 厚度较等效热容模型厚。这一差异是由于显热容模 反复利用该解析解求解各时段上的温度场, 便可以 型没有考虑上体冻结状态下存在未冻水而造成的, 获得温度场在全时间域上的演变过程。 一般土体冻结特性越好,两组模型计算结果的差异 城显著 4算例分析 利用第3节中的半解析方法 对具体条件下的 土体冻结过程进行了温度场计算。 土体孔隙率为 048,初始体积含水率洗取两种计算条件:a,=03 ,=0.18:土体的冻结特性参考文献[61也选取两和 计算冬件分别表示为,,《4=02 B033. 40.1 B ,前者冻结特性较好 (即冻结状 400 800 120 下含有更多的未冻水),后者冻结特性较差。计算 时间/m 柱长为H=0.1m,初始温度为均匀分布6℃,冻结 用3两组捕型冻深发展曲线对比 开始后暖端恒定在T=6℃,冷端恒定在T。= Fig.3 Comp ison freezine fronts of two models 10m 4.1半解析解与数值解对比 曲线 文献[1-14)中有半解析解与简单条件下的角 析解进行的对比,本节主要对半解析解与文献[5]叶 66 由线2 的数值解进行对比,土体初始体积含水率为1,而 88 未冻水关系为0:。半解析解分层间距为0.25mm 时间步长为1s,数值解网格划分与文献5]相同, 这些都是经过试算后的网格独立解 400 800 时/min 120 1600 图2为半解析解与数值解的计算结果在各个时 刻的对比,两者计算结果的吻合验证了半解析解的 图4两组模型冻深发展曲线对比 正确性。 两组模型计算结果的差异可以从未冻水的角 05h 度进行进一步解释。显热容模型不考虑未冻水的存 2 h 在,其冻结过程中土体释放的潜热要高于等效热容 4日 模型,因而其冻结锋面推进速度在瞬态阶段较慢 。折解 给定边界温度时,接近稳态时的温度场分布取 决于导热系数分布,冻土区长度可以利用土柱各处 热流相等得到, 23 45678910 距暖城距离/cm H(T,-T) (33) (T.-T入u/2:)+(T-T) Fig.2 Com 式中:为冻土区厚度:T为冻结温度:元、 and numerical solution 为未冻土区及冻土区平均导热系数。 42等效热容模型与显热容模型对比 由于显热容模型不考虑未冻水的存在,其元:偏 本节进行等效热容模型(模型1)与显热容模 大(见式(4)),由式(33)可知,这将导致其最终 型(模型2)的对比,等效热容模型采用本文半解 冻土区厚度较等效热容模型计算结果厚 土体冻结 析解计算,计算参数与4.1节相同,显热容模型则 特性越好,考虑与不考虑未冻水产生的差异就越大, 采用文献「4数值解计算。图3、4为两组模型计算 从而导致两组模型计算结果的差异就越显著。 1002016h ou al Electronic Publishing House All right rved. hup www.cnki.ne
312 岩 土 力 学 2011 年 上式在计算中可以通过数值积分获得,也可以 按文献[11–14],取 1 , ( ) k T z i t − ∗ 为 i 层的均值温度 1 , k Ti t − ∗ 。 利用式(9),将 (1) Ti 与 (2) Ti 叠加后,即可以得 到 k 时段上温度场的解析解答。在每一时段上,温 度场的解析解均具有相同形式,仅计算参数改变, 反复利用该解析解求解各时段上的温度场,便可以 获得温度场在全时间域上的演变过程。 4 算例分析 利用第 3 节中的半解析方法,对具体条件下的 土体冻结过程进行了温度场计算。土体孔隙率为 0.48,初始体积含水率选取两种计算条件:θ1 = 0.3, θ2 = 0.18;土体的冻结特性参考文献[6]也选取两种 计算条件,分别表示为:θu1(A=0.2,B=0.3),θu2 (A=0.1,B=0.5),前者冻结特性较好(即冻结状态 下含有更多的未冻水),后者冻结特性较差。计算土 柱长为 H = 0.1 m,初始温度为均匀分布 6℃,冻结 开始后暖端恒定在 Tw = 6 ℃,冷端恒定在 Tc = -10 ℃。 4.1 半解析解与数值解对比 文献[11–14]中有半解析解与简单条件下的解 析解进行的对比,本节主要对半解析解与文献[5]中 的数值解进行对比,土体初始体积含水率为 θ1,而 未冻水关系为 θu1。半解析解分层间距为 0.25 mm, 时间步长为 1 s,数值解网格划分与文献[5]相同, 这些都是经过试算后的网格独立解。 图 2 为半解析解与数值解的计算结果在各个时 刻的对比,两者计算结果的吻合验证了半解析解的 正确性。 图 2 半解析解与数值解对比 Fig.2 Comparison between semi-analytical solution and numerical solution 4.2 等效热容模型与显热容模型对比 本节进行等效热容模型(模型 1)与显热容模 型(模型 2)的对比,等效热容模型采用本文半解 析解计算,计算参数与 4.1 节相同,显热容模型则 采用文献[4]数值解计算。图 3、4 为两组模型计算 的各条件下土体冻结锋面的推进曲线。 两组模型计算结果对比表明:在瞬态阶段,显 热容模型计算的冻结锋面推进速度较等效热容模型 慢;而在接近稳态阶段,显热容模型计算的冻土区 厚度较等效热容模型厚。这一差异是由于显热容模 型没有考虑土体冻结状态下存在未冻水而造成的, 一般土体冻结特性越好,两组模型计算结果的差异 越显著。 图 3 两组模型冻深发展曲线对比 Fig.3 Comparison freezing fronts of two models 图 4 两组模型冻深发展曲线对比 Fig.4 Comparison freezing fronts of two models 两组模型计算结果的差异可以从未冻水的角 度进行进一步解释。显热容模型不考虑未冻水的存 在,其冻结过程中土体释放的潜热要高于等效热容 模型,因而其冻结锋面推进速度在瞬态阶段较慢。 给定边界温度时,接近稳态时的温度场分布取 决于导热系数分布,冻土区长度可以利用土柱各处 热流相等得到, f f c wf fc u f ( ) ( )( / ) ( ) HT T H T T TT λ λ − = − +− (33) 式中: f H 为冻土区厚度;Tf 为冻结温度;λu 、λf 为未冻土区及冻土区平均导热系数。 由于显热容模型不考虑未冻水的存在,其λf 偏 大(见式(4)),由式(33)可知,这将导致其最终 冻土区厚度较等效热容模型计算结果厚。土体冻结 特性越好,考虑与不考虑未冻水产生的差异就越大, 从而导致两组模型计算结果的差异就越显著

增刊1 周扬等:土体一维冻结问题温度场半解析解 313 在冻结诱导水流较弱的情形下,采用等效热容 freezing Chinese Journal of Geotechnical 模刑讲行十体族结温度场计算是较完盖的间,此时 若采用显热容模型, ce lens the for froct ho 则必将高估接近稳态时的冻士 区厚度,对于冻结特性较好的土体 这一效果将 为显著,在人工冻结领域,该结果是偏于不安全的。 王家澄,张立新。冻土物理学.北京:科学 5结论 [8]FAROUKIOT.Thermal properties of soils[M].Germany (1)针对士体的一维冻结过程,采用考虑士 ns Tech Public 体冻结状态下未冻水存在的等效热容模型,建立了 1998 其温度场计算的半解析方法,并与相关文献中的数 LI Hong-sheng.LIU Zeng-li,LI Nan-sheng.Afrost heave 值解答进行了对比,验证了方法的正确性。 e an (2)竿效热容横刑与品热容模刑计算结果的 对比表明:在瞬态阶段 ,显热容模型计算的冻结钤 University of Tech gy,1998,38129-33. 面推进速度较等效热容模型慢:而在接近稳态阶段, 周因 显热容模型计算的冻土区厚度较等效热容模型厚。 产生这一差异是由于显热容模型没有考虑土体冻结 ZHOU Jin-sheng ZHOU Gug ing,MA Wei,et al 状态下存在未冻水而造成的。在冻结透导水流较弱 Experimental research on controlling frost heave for 采用显热容模率 2006.3561708-712. 应用于人工冻结设计是偏于不安全的。 山谢康和,郑 ,变荷载下成层地基一维 (3)对于实际工程中的成层十体,也可以第 用本文的方法讲行求解,其计算过程中的分层分两 步进行。首先,以土体天然界面进行 次分层: XIE Kang-he,ZHENG Hui,LI Bing-he.et al Analysis of one dimensional nonlinear consolidation of layered soil 后在每 一层士体中再进行 一次分层 而其余求解 g小 骤与均匀土层完全相同。 43 参考文献 四李冰游和作 等初始有效应 1.1999 山胡向 LI Bing-be XIE Kang-he YING Hong-wei et al 555 Sem analytical solution of nonlinear HU Xiang-dong.HUANG Feng.BAI Nan.Models of rsity [13)李冰河,谢康和,应宏伟 等.变荷载下软黏士非线性 2008.374550-555. 维固结半解析解)岩土工程学报,19,21)288 [O'NEILL K.MILLER R D.Exploration of a rigid ice heave Water Resoures Research. Sem [3]SHEN M.BRANKO L.Modelling of coupled heat. ation of soft clay und moisture and stress field in freezing soil[J].Cold Regions of 1999.2I3288-293 198 码度场数值模拟的 [14蓝柳和,谢康和。成层软黏土地基黏弹性一锥周结半 政进中国矿业大学学报,2005,342179-183. 解析解)土木工程学报,2003,364105 -110 SHANG Xiang-yu,ZHOU Guo-qing,BIE Xiao-yong LAN LI Kang solida 0n9 2005.3i21179-183 36M4105-110 )周扬,周国庆.土壤冻结水热合有限容积模拟研 R L.STEIN J R. On Lo the So HOU 010,323 440 -40 Mechanics and Foundations Division.ASCE.1970 964)1499-1504 1994-016 China Academic Joural Electronic Publishing House.All rights reserved. http://www.cnki.ne
增刊 1 周 扬等:土体一维冻结问题温度场半解析解 313 在冻结诱导水流较弱的情形下,采用等效热容 模型进行土体冻结温度场计算是较完善的[5],此时 若采用显热容模型,则必将高估接近稳态时的冻土 区厚度,对于冻结特性较好的土体,这一效果将更 为显著,在人工冻结领域,该结果是偏于不安全的。 5 结 论 (1)针对土体的一维冻结过程,采用考虑土 体冻结状态下未冻水存在的等效热容模型,建立了 其温度场计算的半解析方法,并与相关文献中的数 值解答进行了对比,验证了方法的正确性。 (2)等效热容模型与显热容模型计算结果的 对比表明:在瞬态阶段,显热容模型计算的冻结锋 面推进速度较等效热容模型慢;而在接近稳态阶段, 显热容模型计算的冻土区厚度较等效热容模型厚。 产生这一差异是由于显热容模型没有考虑土体冻结 状态下存在未冻水而造成的。在冻结诱导水流较弱 的情形下,土体冻结特性越好,采用显热容模型进 行温度场计算产生的误差越显著,并且其计算结果 应用于人工冻结设计是偏于不安全的。 (3)对于实际工程中的成层土体,也可以采 用本文的方法进行求解,其计算过程中的分层分两 步进行。首先,以土体天然界面进行一次分层;然 后在每一层土体中再进行一次分层,而其余求解步 骤与均匀土层完全相同。 参 考 文 献 [1] 胡向东, 黄峰, 白楠. 考虑土层冻结温度时人工冻结温 度场模型[J]. 中国矿业大学学报, 2008, 37(4): 550- 555. HU Xiang-dong, HUANG Feng, BAI Nan. Models of artificial frozen temperature field considering soil freezing point[J]. Journal of China University of Mining & Technology, 2008, 37(4): 550-555. [2] O’NEILL K, MILLER R D. Exploration of a rigid ice model of frost heave[J]. Water Resources Research, 1985, 21(3): 281-296. [3] SHEN M, BRANKO L. Modelling of coupled heat, moisture and stress field in freezing soil[J]. Cold Regions Science and Technology, 1987 , 14: 237-246. [4] 商翔宇, 周国庆, 别小勇. 冻结土壤温度场数值模拟的 改进[J]. 中国矿业大学学报, 2005, 34(2): 179-183. SHANG Xiang-yu, ZHOU Guo-qing, BIE Xiao-yong. Numerical simulation improvement of freezing soil’s temperature field[J]. Journal of China University of Mining & Technology, 2005, 34(2): 179-183. [5] 周扬, 周国庆. 土壤冻结水热耦合有限容积模拟研 究[J]. 岩土工程学报, 2010, 32(3): 440-446. ZHOU Yang, ZHOU Guo-qing. Finite volume simulation for coupled moisture and heat transfer during soil freezing[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(3): 440-446. [6] NIXON J F. Discrete ice lens theory for frost heave in soils[J]. Canadian Geotechnical Journal, 1991, 28: 843 -859. [7] 徐学祖, 王家澄, 张立新. 冻土物理学[M]. 北京: 科学 出版社, 2001. [8] FAROUKI O T. Thermal properties of soils[M]. Germany: Trans. Tech. Publications, 1986. [9] 李洪升, 刘增利, 李南生. 基于冻土水分温度和外荷载 相互作用的冻胀模式[J]. 大连理工大学学报, 1998, 38(1): 29-33. LI Hong-sheng, LIU Zeng-li, LI Nan-sheng. A frost heave model based on moisture temperature and applied load interaction in frozen soils[J]. Journal of Dalian University of Technology, 1998, 38(1): 29-33. [10] 周金生, 周国庆, 马巍, 等. 间歇冻结控制人工冻土冻 胀的试验研究[J]. 中国矿业大学学报, 2006, 35(6): 708 -712. ZHOU Jin-sheng, ZHOU Guo-qing, MA Wei, et al. Experimental research on controlling frost heave for artificial frozen soil with intermission freezing method[J]. Journal of China University of Mining & Technology, 2006, 35(6): 708-712. [11] 谢康和, 郑辉, 李冰河, 等. 变荷载下成层地基一维非 线性固结分析[J]. 浙江大学学报(工学版), 2003, 37(4): 426-431. XIE Kang-he, ZHENG Hui, LI Bing-he, et al. Analysis of one dimensional nonlinear consolidation of layered soils under time-dependent loading[J]. Journal of Zhejiang University (Engineering Science), 2003, 37(4): 426- 431. [12] 李冰河, 谢康和, 应宏伟, 等. 初始有效应力沿深度变 化的非线性一维固结半解析解[J]. 土木工程学报, 1999, 32(6): 47-52. LI Bing-he, XIE Kang-he, YING Hong-wei, et al. Semi-analytical solution of nonlinear consolidation considering the initial effective stress distribution[J]. China Civil Engineering Journal, 1999, 32(6): 47-52. [13] 李冰河, 谢康和, 应宏伟, 等. 变荷载下软黏土非线性 一维固结半解析解[J]. 岩土工程学报, 1999, 21(3): 288 -293. LI Bing-he, XIE Kang-he, YING Hong-wei, et al. Semi-analytical solution of one dimensional nonlinear consolidation of soft clay under time-dependent loading[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(3): 288-293. [14] 蓝柳和, 谢康和. 成层软黏土地基黏弹性一维固结半 解析解[J]. 土木工程学报, 2003, 36(4): 105-110. LAN Liu-he, XIE Kang-he. Semi-analytical solution of one-dimensional visco-elastic consolidation for layered soft clay[J]. China Civil Engineering Journal, 2003, 36(4): 105-110. [15] SCHIFFMAN R L, STEIN J R. One-dimensional consolidation of layered systems[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1970, 96(4): 1499-1504