
第29卷第9期 Vol.29 No.9 工程 力学 2012年9月Sep.2012 ENGINEERING MECHANICS 193 文章编号:1000-4750(2012)09-0193-07 谐波热作用下墙体温度场的解析解 梁建国,周莉,杨牧 (长沙理工大学士木与建筑学院,潮南,长沙41011 摘要:超长结构设计时应分析墙体温度场变化产生的温度应力,以控制温度作用墙体产生裂缝。针对谐波热价 用下的单层墙,采取变量分离法求解第一类边界条件下的热传导微分方程,得到单层墙温度场的解析表达式。以 此为基础,采用两层墙接触面处温度和热流相等的基本假设,推导了谐波热作用下第一类和第三类边界条件时多 层墙温度场的解析解,为培体温度应力分析和裂缝挖制提供了理论基础。利用推导的墙体温度场计算公式,对外 墙外保温墙体的温度场进行了分析和研究。 关键词:培:温度场:裂缝控制:热传导:谐波热:变量分离法:保温隔热 中图分类号:TU11:TU352.59 文献标志码:A d10.6052.ism.100-4750,2010.12.0902 ANALYTICAL SOLUTION FOR TEMPERATURE FIELD IN WALLS SUBJECTED TO HARMONIC HEAT LIANG Jian-guo,ZHOU Li,YANG Mu (School of Civil EnginceringArchitecture.Changsha University of Scince&Technology.Changsha Hunn011China) Abstract:In overlong structure design,the temperature stress of walls caused by temperature field changes should be analyzed in order to control temperature cracks in the walls.For single-layer walls subjected to periodic harmonic heat,the heat transfer differential qation in the first boundary condition was solved by a variable separation method.and the analytical solution for the temperature field of a single-laver wall was received.Based on this solution and the assumption that the temperature and heat flow at the contact interface of two lavers are equal,the analytical solutions of a temperature field of a multilayer wall was obtained while cconsidering the heat exchange between the wall and the air.and provided a theoretical basis for the temperature stress analysis and crack controlling in walls.Using this formula for the temperature field in walls,the temperature field in the exteral insulation wall was researched Key words:wall;temperature field;crack control;heat transfer;harmonic heat:variable separation;insulation 超长混凝土或砌体房屋顶部墙体通常由于墙 消除温度作用。然而,对于超长混凝土高层建筑, 体与屋面结构之间的温差作用导致开裂,底部墙体 设置伸缩缝往往既不美观,也不经济。将温度作用 通常由于墙体的温度收缩受到地基约束而产生开 当成荷载进行超长建筑的结构设计的方法,已经取 裂。这些温度裂缝产生的原因一般认为是:墙体 得了一定成效5-。目前针对围护结构温度荷载的 温度场发生改变,并受到相互约束而产生拉应力 温度场研究方法仅仅局限于有限差分法或者有限 当拉应力超过结构材料极限抗拉强度时,就会出现 元法9-0,这些数值解法的问题在于除了边界条件 温度裂缝叫。 外,还应赋予初值条件才能求解,而周期性谐波热 在桥梁及水利工程中,对温度应力已经有较多 作用下的 度场属于准稳态非稳定热传导,与初 的研究),而房屋建筑一般采用经验的变形缝来 条件无关叫,因此,所预估的初值难免给计算结果 收日期:2010-2-10:修日期:2012-01-05 杨牧(1986-).男。新江宁波人,士生。从事钢第混凝土及商体结构研究下-ma1729420549 @gg.com 1994-2015 China Acade nal Electronic Publishing House ww.cnki.ne
第 29 卷第 9 期 Vol.29 No.9 工 程 力 学 2012 年 9 月 Sep. 2012 ENGINEERING MECHANICS 193 ——————————————— 收稿日期:2010-12-10;修改日期:2012-01-05 通讯作者:梁建国(1963―),男,湖南常宁人,教授,工学硕士,从事钢筋混凝土及砌体结构研究(E-mail: jgliang1963@163.com). 作者简介:周 莉(1986―),女,湖南永州人,硕士生,从事钢筋混凝土及砌体结构研究(E-mail: 48924279@qq.com); 杨 牧(1986―),男,浙江宁波人,硕士生,从事钢筋混凝土及砌体结构研究(E-mail: 729420549@qq.com). 文章编号:1000-4750(2012)09-0193-07 谐波热作用下墙体温度场的解析解 梁建国,周 莉,杨 牧 (长沙理工大学土木与建筑学院,湖南,长沙 410114) 摘 要:超长结构设计时应分析墙体温度场变化产生的温度应力,以控制温度作用墙体产生裂缝。针对谐波热作 用下的单层墙,采取变量分离法求解第一类边界条件下的热传导微分方程,得到单层墙温度场的解析表达式。以 此为基础,采用两层墙接触面处温度和热流相等的基本假设,推导了谐波热作用下第一类和第三类边界条件时多 层墙温度场的解析解,为墙体温度应力分析和裂缝控制提供了理论基础。利用推导的墙体温度场计算公式,对外 墙外保温墙体的温度场进行了分析和研究。 关键词:墙;温度场;裂缝控制;热传导;谐波热;变量分离法;保温隔热 中图分类号:TU111;TU352.59 文献标志码:A doi: 10.6052/j.issn.1000-4750.2010.12.0902 ANALYTICAL SOLUTION FOR TEMPERATURE FIELD IN WALLS SUBJECTED TO HARMONIC HEAT LIANG Jian-guo , ZHOU Li , YANG Mu (School of Civil Engineering & Architecture, Changsha University of Science & Technology, Changsha, Hunan 410114, China) Abstract: In overlong structure design, the temperature stress of walls caused by temperature field changes should be analyzed in order to control temperature cracks in the walls. For single-layer walls subjected to periodic harmonic heat, the heat transfer differential equation in the first boundary condition was solved by a variable separation method, and the analytical solution for the temperature field of a single-layer wall was received. Based on this solution and the assumption that the temperature and heat flow at the contact interface of two layers are equal, the analytical solutions of a temperature field of a multilayer wall was obtained while cconsidering the heat exchange between the wall and the air, and provided a theoretical basis for the temperature stress analysis and crack controlling in walls. Using this formula for the temperature field in walls, the temperature field in the external insulation wall was researched. Key words: wall; temperature field; crack control; heat transfer; harmonic heat; variable separation; insulation 超长混凝土或砌体房屋顶部墙体通常由于墙 体与屋面结构之间的温差作用导致开裂,底部墙体 通常由于墙体的温度收缩受到地基约束而产生开 裂[1]。这些温度裂缝产生的原因一般认为是:墙体 温度场发生改变,并受到相互约束而产生拉应力, 当拉应力超过结构材料极限抗拉强度时,就会出现 温度裂缝[2]。 在桥梁及水利工程中,对温度应力已经有较多 的研究[3―4],而房屋建筑一般采用经验的变形缝来 消除温度作用。然而,对于超长混凝土高层建筑, 设置伸缩缝往往既不美观,也不经济。将温度作用 当成荷载进行超长建筑的结构设计的方法,已经取 得了一定成效[5―8]。目前针对围护结构温度荷载的 温度场研究方法仅仅局限于有限差分法或者有限 元法[9―10],这些数值解法的问题在于除了边界条件 外,还应赋予初值条件才能求解,而周期性谐波热 作用下的温度场属于准稳态非稳定热传导,与初值 条件无关[11],因此,所预估的初值难免给计算结果

194 程 带来误差 采用分离变量法, 可求得微分方程式(la)的通 围护结构温度场的分布和变化规律除与保温 解为 隔热层的构造和热工特性有关外,还与室外空气温 T(x.t)=(C coshx+C2 sinhkx)e (2) 度和太阳辐射强度有关。室外空气温度和太阳辐射 式中, C2为积分常数 强度具有逐日、逐年周期变化的特性,利用傅里叫 由式(1b)式(1c),得: 级数,可以将这 温度作用简化成谐波热作用和利 C cosh0+C2 sinh0=0 (3a 态温度作用叠加凶。稳态温度作用可以用很简单的 (C cosh+C:sinh)e=Acos(ar)(3b) 线性分布来计算多层墙的温度场,而非稳态热作用 由式(3),得 度场计算却非常麻。在建热丁设计中,尽管 C.sinbke =Acos(o) (4) 可以用谐波反应法、反应系数法、乙 递函数法 多种方法来研究围护结构的传热过程3-间,但这些 显然,若k为实数,式(4)左边不是周期函数 等号不可能成立,因而k不可能取实数。若设 方法只根据采暖通风的要求得出了围护结构表面 k=α+í为一复数,则方程的解为一复变函数。 温度和热流的变化规律,忽视了围护结构温度场的 变化规律 为此,改变边界条件式(1c为: 本文采取变量分离法求解一侧温度恒定为0、 T(x,t)s= (5) 另一侧作用谐波热作用下单层培的温度场,并通过 值得注意的是,实际的边值是式(⑤)的实部。 式(4)改写为: 叠加原理得到两到均作用进波热时单层墙的温度 场, 在不考 接触面的热阻和热容后建立在诰波 Ca sinh=Aci (6 作用下的多层墙温度场的求解方法。 式(6)对任意1均满足的条件是a=i,或 1 室外谐波热作用室内恒温时 瓜=土品0+).另外,当1=0时: 单层墙的温度场 C2 将单层墙看成是匀质无限大平板,单层培两侧 sinh (7) 的热传导问题便简化为一维热传导问题。一般地, 将系数C1、C2、k代入式(2),并令=6√o/(2a) 墙体两侧作用了周期性谐波热或稳定热源(如:空温 刀=x/6,∈(0,),整理得到一个复函数。由于对 或采暖时室内一侧),在求解这种复杂的热作用 应于实部边值的解是上述解的实部,因此,该复 体温度场之前,先求出室外谐波热作用、室内温度 函数的实部为室外谐波热作用室内恒温时单层墙 恒定为0时单层墙的温度场,然后利用叠加法求得 的温度场: T(n,)=Xn)Acos[+p(】 (8) 不同热作用下墙体温府场。 室外谐波热作用、室内温度恒定为0时, 按照 式中 第一类边界条件,单层墙的热传导控制方程为: x)=√E)+F()(幅值衰减系数) ∂rc,=a0Tx, (1a) T(x.t)0=0 1b E(n)=(sinhocososinh(on)cos(on)+cosho. T(x,r)=Acos(@r) (Ie) sinocosh(on)sin()/(sinh+sin) 式中:T(x,)为温度分布函数:6m为墙厚度: ()=(sinhocosocosh(on)sin(on)-cosho a(m2h)为材料的导温系数,a= :wm·K) sinosinh(on)cos(on))/(sinh2+sin2) 为材料的导热系数: 2 室内外有初相位的谐波热作用下 单层墙的温度场 值:w/(rad/h)为谐波热变化的角须率,=2,Z 2.1 7 室外有初相位的谐波热作用室内恒温时 为谐波热变化周期。 单层墙的温度场 当室外有幅值为A)、初相位为的余弦谐 21994-2015Chim Academic Jour al Electronic Publishing www.cnki.ne
194 工 程 力 学 带来误差。 围护结构温度场的分布和变化规律除与保温 隔热层的构造和热工特性有关外,还与室外空气温 度和太阳辐射强度有关。室外空气温度和太阳辐射 强度具有逐日、逐年周期变化的特性,利用傅里叶 级数,可以将这种温度作用简化成谐波热作用和稳 态温度作用叠加[12]。稳态温度作用可以用很简单的 线性分布来计算多层墙的温度场,而非稳态热作用 温度场计算却非常麻烦。在建筑热工设计中,尽管 可以用谐波反应法、反应系数法、Z 传递函数法等 多种方法来研究围护结构的传热过程[13―14],但这些 方法只根据采暖通风的要求得出了围护结构表面 温度和热流的变化规律,忽视了围护结构温度场的 变化规律。 本文采取变量分离法求解一侧温度恒定为 0、 另一侧作用谐波热作用下单层墙的温度场,并通过 叠加原理得到两侧均作用谐波热时单层墙的温度 场,在不考虑接触面的热阻和热容后建立在谐波热 作用下的多层墙温度场的求解方法。 1 室外谐波热作用室内恒温时 单层墙的温度场 将单层墙看成是匀质无限大平板,单层墙两侧 的热传导问题便简化为一维热传导问题。一般地, 墙体两侧作用了周期性谐波热或稳定热源(如:空调 或采暖时室内一侧),在求解这种复杂的热作用下墙 体温度场之前,先求出室外谐波热作用、室内温度 恒定为 0 时单层墙的温度场,然后利用叠加法求得 不同热作用下墙体温度场。 室外谐波热作用、室内温度恒定为 0 时,按照 第一类边界条件,单层墙的热传导控制方程为: 2 2 T xt T xt (,) (,) a t x ∂ ∂ = ∂ ∂ (1a) 0 ( , )| 0 T xt x= = (1b) ( , ) | cos( ) T xt A t x=δ = ω (1c) 式中:T xt (,) 为温度分布函数;δ /m 为墙厚度; a /(m2 /h)为材料的导温系数,a c λ ρ = ;λ /(W/m·K) 为材料的导热系数; c /(kJ/kg·K)为材料的比热; ρ /(kg/m3 )为材料的密度;A/(℃)为谐波热波动幅 值;ω/(rad/h)为谐波热变化的角频率, 2π Z ω = ,Z/h 为谐波热变化周期。 采用分离变量法,可求得微分方程式(1a)的通 解为: 1 2 ( , ) ( cosh sinh )ekat T x t C kx C kx = + (2) 式中,C1、C2 为积分常数。 由式(1b)、式(1c),得: 1 2 C C cosh 0 sinh 0 0 + = (3a) 1 2 ( cosh sinh )e cos( ) kat C kC k A t δδω + = (3b) 由式(3),得: 2 sinh e cos( ) kat C k At δ ω = (4) 显然,若 k 为实数,式(4)左边不是周期函数, 等号不可能成立,因而 k 不可能取实数。若设 k = + α βi 为一复数,则方程的解为一复变函数。 为此,改变边界条件式(1c)为: i = ( , )| e t T xt A x ω δ = (5) 值得注意的是,实际的边值是式(5)的实部。 式(4)改写为: i 2 sinh e e kat t Ck A ω δ = (6) 式(6)对任意 t 均满足的条件是 ka =ωi ,或 (1 i) 2 k a ω =± + 。另外,当t = 0时: 2 sinh A C kδ = (7) 将系数 C1、C2、k 代入式(2),并令φδ ω = /(2 ) a 、 η = x/δ ,η ∈(0,1),整理得到一个复函数。由于对 应于实部边值的解是上述解的实部[13],因此,该复 函数的实部为室外谐波热作用室内恒温时单层墙 的温度场: Tt A t ( , ) ( ) cos[ ( )] η χ = + ′ ′ η ω ϕ η (8) 式中: 2 2 χ′() () () η ηη = + E F (幅值衰减系数) ( ) ( ) arctan ( ) F E η ϕ η η ′ = (时间延迟) E( ) (sinh cos sinh( )cos( ) cosh η φφ φ = +⋅ η φη φ 2 2 sin cosh( )sin( ))/(sinh sin ) φ φη φη φ φ + F( ) (sinh cos cosh( )sin( ) cosh η φφ φ = −⋅ η φη φ 2 2 sin sinh( )cos( )) / (sinh sin ) φ φη φη φ φ + 2 室内外有初相位的谐波热作用下 单层墙的温度场 2.1 室外有初相位的谐波热作用室内恒温时 单层墙的温度场 当室外有幅值为 (o) A 、初相位为 (o) ψ 的余弦谐

程 力 学 波热作用,室内恒温且温度为0时,已有研究证 明,墙体的温度场与没有初相位谐波热作用相比 较,其波动频率相同,相位相差yo,由式(8)得单 G(n)=((sinhocos+coshosin)cosh(on) 层墙的温度场: coston)-(sinhocoso-coshosin). T(n.t)=()A cos[a+'(n)+](9) sinh(on)sin(o))/(sinh2+sin) 2.2室内有初相位的诺波热作用时单层墙的温度场 H(n)=((sinhocoso-coshosino)cosh(on) 将式(9)中7换成1-n,4o换成40,换 coston)+(sinhocos+coshosino). 成,得: sinh(o)sin())/(sinh2+sin) T(n,t)=X1-)cos[+p01-m+]10) 2.4讨论 23室内外有初相位的谐波热作用时单层墙的 1)稳态温府场 温度场及热流 若0=0(p=0小0=0、0=0,相当于 假设单层墙室内外作用谐波热: 培内外表面分别作用恒温40和,墙的温度场 室内:To(0)=cos(am+w) 属于稳态温度场.因为m sinhe=1, 宝外:To(t)=o)cosm+o) sin2=l、lim 根据叠加原理(如图1,由式(9) 式(10),得 所以E)=lmF)=0.由式.得到 到室内外作用谐波热时单层墙的温度场; 墙的温度场: T(n.t)=x(n)A cos ox +an 11) (13) 式中: T(n,)=0+(1-n)5]4o )=V)2+2 式(13)即为墙内外表面作用恒温0和时 的稳态温度场计算公式,与文献14一致。 a(n)=tan- n 2)谐波热作用下无限厚墙体 若室内边界温度为T(n,)n=Acos(a)), (n)=E(n)cosyAo) -F(n)sinw+ Tm,)儿=0,由式(11)中系数为 E(1-n)cosu-F(1-n)sinw 7)=E(1-1) (14a) )=E(n)sin)+F(n)cos()+ E(1-n)siny F(1-n)cosv )=F0-) (14b) 5=A014@(室内外空气温度幅值之比值): (n)=coshscoss-(sinhocoshosinhscoss+ sinocosocoshssins)/(sinh2+sin2) n)=sinssinhs+(sincososinhs coss- sinhocoshosinscoshs)/(sinh+sin) 对无限厚培体,即6→,。→,由以上两 式求极限,得到:)=e'coss:)=esins, 图1叠加原理 代入式(1,得到表面作用谐波热的无限厚墙体温 Fig.l 度场: 根据傅里叶定律,任意x处的热流为: (15) 9.)=-20加n.0 δan 式(15)与文献13推导的谐波热作用下无限厚 G()cos)-H()sin) 墙体温度场公式一致。 EG(1-n)cosw(+H(1-n)siny ]cos(ax)- 3)温度分布与墙热惰性指标D的关系 [G(sin+H()cos 由前述定义,我们知道: 5G(1-n)siny)-H(1-n)cosw ]sin(ax):(12) 1994-2015 China Academie Joural Electronic Publishing House.All rights reserved.http://www.enki.ne
工 程 力 学 195 波热作用,室内恒温且温度为 0 时,已有研究证 明[14],墙体的温度场与没有初相位谐波热作用相比 较,其波动频率相同,相位相差ψ(o),由式(8)得单 层墙的温度场: (o) (o) Tt A t ( , ) ( ) cos[ ( ) ] η χη ω ϕη ψ = ++ ′ ′ (9) 2.2 室内有初相位的谐波热作用时单层墙的温度场 将式(9)中η 换成1−η , (o) A 换成 (i) A , (o) ψ 换 成 (i) ψ ,得: (i) (i) Tt A t ( , ) (1 ) cos[ (1 ) ] η χ η ωϕ ηψ = − + −+ ′ ′ (10) 2.3 室内外有初相位的谐波热作用时单层墙的 温度场及热流 假设单层墙室内外作用谐波热: 室内: (i) (i) (i) Tt A t ( ) cos( ) = + ω ψ 室外: (o) (o) (o) TtA t ( ) cos( ) = + ω ψ 根据叠加原理(如图 1)[14],由式(9)、式(10),得 到室内外作用谐波热时单层墙的温度场: (o) Tt A t ( , ) ( ) cos[ ( )] η χ = + η ω ϕ η (11) 式中: 2 2 χ() () () η θη ϑη = + ; 1 ( ) ( ) tan ( ) ϑ η ϕ η θ η − = ; (o) (o) θη η ψ η ψ ( ) ( )cos ( )sin =−+ E F (i) (i) ξE F (1 )cos (1 )sin − −− η ψ ξ η ψ ; (o) (o) ϑη η ψ η ψ ( ) ( )sin ( )cos =+ + E F (i) (i) ξE F (1 )sin (1 )cos − +− η ψ ξ η ψ ; (i) (o) ξ = A A/ (室内外空气温度幅值之比值)。 图 1 叠加原理 Fig.1 Superposition principle 根据傅里叶定律,任意 x 处的热流为: ( ,) ( ,) T t q t λ η η δ η ∂ =− = ∂ (o) (o) (o) − −− rA G H {[ ( )cos ( )sin η ψ ηψ (i) (i) ξ η ψξ ηψ ω GH t (1 )cos (1 )sin ]cos( ) − +− − (o) (o) [ ( )sin ( )cos G H ηψ η ψ + − (i) (i) ξGH t (1 )sin (1 )cos ]sin( )} − −− η ψ ξ η ψ ω (12) 式中: 2 r a φλ ω λ δ = = ; G( ) ((sinh cos cosh sin )cosh( ) η φ φ φφ φ =+ ⋅ η cos( ) (sinh cos cosh sin ) φη −−⋅ φ φ φφ 2 2 sinh( )sin( )) / (sinh sin ) φη φη φ φ + H( ) ((sinh cos cosh sin )cosh( ) η φ φ φφ φ =− ⋅ η cos( ) (sinh cos cosh sin ) φη ++⋅ φ φ φφ 2 2 sinh( )sin( )) / (sinh sin ) φη φη φ φ + 2.4 讨论 1) 稳态温度场 若ω = 0 (φ = 0 )、 (i) ψ = 0 、 (o) ψ = 0,相当于 墙内外表面分别作用恒温 (i) A 和 (o) A ,墙的温度场 属于稳态温度场。因为 0 sin lim 1 φ φ → φ = 、 0 sinh lim 1 φ φ → φ = , 所以 0 lim ( ) 1 E φ η → = 、 0 lim ( ) 0 F φ η → = 。由式(11),得到 墙的温度场: (o) Tt A ( , ) [ (1 ) ] η η ηξ = +− (13) 式(13)即为墙内外表面作用恒温 (i) A 和 (o) A 时 的稳态温度场计算公式,与文献[14]一致。 2) 谐波热作用下无限厚墙体 若室内边界温度为 0 Tt A t ( , ) | cos( ) η η= = ω , 1 T t ( , )| 0 η η= = ,由式(11)中系数为: θη η ( ) (1 ) = − E (14a) ϑη η ( ) (1 ) = − F (14b) 令 2 s x a ω = ,则有: θ η( ) cosh cos (sinh cosh sinh cos =− + s s ss φ φ 2 2 sin cos cosh sin ) / (sinh sin ) φφ φ φ s s + ϑ η( ) sin sinh (sin cos sinh cos =+ − s s ss φ φ 2 2 sinh cosh sin cosh ) / (sinh sin ) φφ φ φ s s + 对无限厚墙体,即δ → ∞ ,φ → ∞ ,由以上两 式求极限,得到: ( ) e cos s θ η s − = ; ( ) e sin s ϑ η s − = − , 代入式(11),得到表面作用谐波热的无限厚墙体温 度场: 2 ( , ) e cos 2 x a T xt A t x a ω ω ω − ⎛ ⎞ = − ⎜ ⎟ ⎝ ⎠ (15) 式(15)与文献[13]推导的谐波热作用下无限厚 墙体温度场公式一致。 3) 温度分布与墙热惰性指标 D 的关系 由前述定义,我们知道: A(i) A(i) A(o) A(o)

196 学 -2 式中:尺为单层墙热阻,R=号:S为单层墙蓄热系 cp风:D为单层墙热惰性指标,D=心。 数,S= 若室外作用幅值为4、初相位为0的余弦 图3多层墙的构成 波热,周期Z=24h,室内恒温为0,由式(11),得到 Fig 3 Composition of multilayer wall 单层培的温度幅值衰减系数)随热惰性指标D 界条件计算。 的变化规律如图2所示。从图2中可以看出:随者 3)多层墙外表面受谐波热作用: 墙体热惰性指标的增加 墙内幅值曲线逐渐减小: 室内:T)=T0(0=Acos(am+) 当D=0时,墙体内温度分布成直线,为稳态温度场 室外:T)=To(0=)cos(a+w) 温度分布:当D<2时,温度场分布接近稳态温度场, 32多层墙界而温度 可按稳态温度场计算方法计算 将各层材料分别看成单层墙,在谐波热作用 下,根据基本假设,两层墙体接触面温度始终相等 因此,两层墙在接触面的温度变化幅值、频率和初 相位都相同。假设k界面上的温度幅值和初相位分 别为A)、),则第k层墙的外侧(=1)及第k+1 层墙的内侧(0)温度均为: T()=)cos(o+) 由式(12,第k层墙在k界面上的热流为 ()=q:()=-G(1)cosw/) H(1)sin w)-g-G(0))+ H:(0)sinw-]cos(G(1)sin 02 0. H(1)cosu)-g-G(0)sin) 图2 H(0)cos]sin() (16 Fig2 同样地,第+1层墙在k界面上的热流为: g0=g1(0,0) 3谐波热作用下多层墙的温度场 -+1Ao{[5+G4+1(0)cosk+- 为了满足建筑节能要求,围护结构由包括保温 ()sin(cos 层在内的层均质材料组成,从内向外分别表示为 (1)sin ]cos()-[G(0) 第1、2、…、k-1、k、k+1、…、n层,各层的几何和物 sin(cos() 理参数符号用下标表示其层编号:各层的界面,从 (17 内向外依次用0.1 、n表示,各界面的物理参数 sin)(1)cos)]sin( 符号用上标表示 其界面编号,如图3所元 第k 根据基本假设,第k层和第什1层在共同界面 的厚度为dm,导温系数为am2h),导热系数 k上的热流在任何时候均应相等,因此,式(16) (WmK),比热/(kJ/(kg-K》,密度Pkgm)。 式(17)必须同时满足: 3.1基本假设 G(1)cosy)H(1)sin) )各层互相紧密接触,在界面处相邻两层的温 5-G40)cosy-+5-H,(0)siny-]= 度相等,沿热流方向前一层的输出热流即为后一层 G(0)co 的输入热流。 +H(0)sin 2)忽略多层墙外表面换热作用,即按第一类边 5G+()cos+5H+1sin] (18) 1994-2015Chim Academic Joumal Electronie Publishing House. www.cnki.net
196 工 程 力 学 1 2π 1 2 2 22 c D RS a Z ω δ ρλ φ δ λ == = = 式中:R 为单层墙热阻,R δ λ = ;S 为单层墙蓄热系 数, 2πc S Z ρλ = ;D 为单层墙热惰性指标,D RS = 。 若室外作用幅值为 (o) A 、初相位为 0 的余弦谐 波热,周期 Z=24h,室内恒温为 0,由式(11),得到 单层墙的温度幅值衰减系数 χ( ) η 随热惰性指标 D 的变化规律如图 2 所示。从图 2 中可以看出:随着 墙体热惰性指标的增加,墙内幅值曲线逐渐减小; 当 D=0 时,墙体内温度分布成直线,为稳态温度场 温度分布;当 D<2 时,温度场分布接近稳态温度场, 可按稳态温度场计算方法计算。 图 2 室外谐波热作用时墙内温度幅值分布 Fig.2 Temperature amplitude distribution in wall subjected to harmonic heat at outdoor 3 谐波热作用下多层墙的温度场 为了满足建筑节能要求,围护结构由包括保温 层在内的 n 层均质材料组成,从内向外分别表示为 第 1、2、···、k−1、k、k+1、···、n 层,各层的几何和物 理参数符号用下标表示其层编号;各层的界面,从 内向外依次用 0、1、···、n 表示,各界面的物理参数 符号用上标表示其界面编号,如图 3 所示。第 k 层 的厚度为 k δ /m,导温系数为 k a /(m2 /h),导热系数λk / (W/(m·K)),比热 k c /(kJ/(kg·K)),密度 ρk /(kg/m3 )。 3.1 基本假设 1) 各层互相紧密接触,在界面处相邻两层的温 度相等,沿热流方向前一层的输出热流即为后一层 的输入热流。 2) 忽略多层墙外表面换热作用,即按第一类边 图 3 多层墙的构成 Fig.3 Composition of multilayer wall 界条件计算。 3) 多层墙外表面受谐波热作用: 室内: (0) (i) (i) (i) T tTt A t ( ) ( ) cos( ) == + ω ψ 室外: ( ) (o) (o) (o) ( ) ( ) cos( ) n TtTt A t == + ω ψ 3.2 多层墙界面温度 将各层材料分别看成单层墙,在谐波热作用 下,根据基本假设,两层墙体接触面温度始终相等, 因此,两层墙在接触面的温度变化幅值、频率和初 相位都相同。假设 k 界面上的温度幅值和初相位分 别为 ( ) k A 、 ( ) k ψ ,则第 k 层墙的外侧(η=1)及第 k+1 层墙的内侧(η=0)温度均为: () () () ( ) cos( ) kk k TtA t = + ω ψ 由式(12),第 k 层墙在 k 界面上的热流为: ( ) (o) ( ) ( ) ( ) (1, ) {[ (1)cos k kk kk k q t q t rA G = =− − ξ ψ ( ) ( ) ( 1) ( 1) k (1)sin (0)cos k kk k H Gk ξ ψξ ψ − − − + ( 1) ( 1) ( ) ( ) (0)sin ]cos( ) [ (1)sin k k kk H tG k k ξ ψ ωξ ψ − − − + ( ) ( ) ( 1) ( 1) (1)cos (0)sin k kk k H G k k ξ ψξ ψ − − − − ( 1) ( 1) (0)cos ]sin( )} k k H t k ξ ψω − − (16) 同样地,第 k+1 层墙在 k 界面上的热流为: ( ) 1 ( ) (0, ) k k qt q t = = + (o) ( +1) ( +1) +1 +1 {[ (0)cos k k k k − − rA G ξ ψ ( +1) ( +1) ( ) ( ) +1 +1 (0)sin (1)cos k kk k H G k k ξ ψξ ψ − + ( ) ( ) ( +1) +1 +1 (1)sin ]cos( ) [ (0) kk k H tG k k ξ ψ ωξ − ⋅ ( +1) ( +1) ( +1) ( ) +1 +1 sin (0)cos (1) kk kk ψξ ψξ + −⋅ H G k k () () () +1 sin (1)cos ]sin( )} kk k ψξ ψ − H t k ω (17) 根据基本假设,第 k 层和第 k+1 层在共同界面 k 上的热流在任何时候均应相等,因此,式(16)、 式(17)必须同时满足: () () () () [ (1)cos (1)sin k kk k kk k rG H ξ ψξ ψ − − ( 1) ( 1) ( 1) ( 1) (0)cos (0)sin ] k kk k G H k k ξ ψξ ψ − −− − + = ( +1) ( +1) +1 +1 [ (0)cos k k k k r G ξ ψ − ( +1) ( +1) +1(0)sin k k Hk ξ ψ − () () () () +1 +1 (1)cos (1)sin ] k kk k G H k k ξ ψξ ψ + (18) 厚度系数η=x/δ 温度场幅值修正系数χ(η) 1.5

程 力 学 197 aG (1)sin)H(1)cos) 三类边界条件下多层培的传热,可以将墙的表面空 -G,(0)sinw-1)-(-H(0)cos)]= 气边界层看成是多层培的一层(如图4),该层只有热 阻没有热容。多层墙内侧空气层内外两侧表面温 5+H+1(0)cosy+-5G41)sinw)- 和热流有如下关系4: )H(1)cos] (19 T(]1 r 式中,)为k界面上温度幅值与室外温度幅值的 g00 (22 比g” 式中:T()、g()分别为室内空气层在0界面 上的温度和热流:T(t)、g(t)分别为室内空气 由于多层平壁内表面、外表面的谐波热幅值及 初相位为己知,该问题共有2m-1)个未知量: 层在1界面上的温度和热流。 5…5、5-以及y、2…g…y- 由式(12,第1层在0界面热流为: g0(t)=g(0.t)= 在墙体的(m-1)个界面上可以根据式(18)、式(19列 出2-1)个方程,采用迭代法解方程组便可得到 G(0)(0)sin 2(n-1)个未知量的解析解 G(1)cosw+(1)sinwcos(aw)- 3.3第k层温度场及其平均温度 [G(0)sinH(0)cos 由式(11)得第k层的温度场: G(1)sin H(1)cos]sin(ax)(23) T(,)=()4ocos[+9(】(20) 由式(22、式(23),得: 式中: T)=T00-g(0=T)-二g(0 ()=Va+(:(m)=tan四 8() 8(n)=E(n)cos)F (n)siny)+ To)=Ao{50cosw0+[5G,(0): u-E(1-)cos1)--F(1-)sin cosuH(0)sinw-G(1)- (n)=E(n)sinw)+F(n)cos+ E:(1-)sinF(1-)cos- cos))sin(H(1 cos(ax)- 第k层平均温度为: sinG()sin .(t)=T(n.t)dn=)cos[ar+](21) H(0)cosG(1)sinwo) 式中: 5oH,(cosw]}sin(ar) 24 无厨+匠:及=m爱 由式(1I).并注意E(0)=0,F(0)=0,E(0 =5)cos)+)sin)+ 1,F()=0,第1层在0界面上的温度: 5 cos-)sin-1 T0(0,)=T(0,)= 及=s5sinw-55cosw+ A(cos)cos(ar)-sinwo)sin(ar))(25) 5k-sin)-)cosw-) 102 5=H0-H,(0):54=G(0-G(0) 考虑空气对流换热时多层墙的 室内 温度场 4.1考虑室内空气对流换热时墙内表面温度 图4室内空气层 假设室内空气余弦谐波热幅值为4、初相 Fig. 为w0,室内空气与墙内侧换热系数为。对于第 由基本假设,0界面上除了热流相等外,温度 994-2015 China Academic Joumal Electronic Publishing House.All rights reserved.http://www.enki.ne
工 程 力 学 197 () () () () [ (1)sin (1)cos k kk k kk k rG H ξ ψξ ψ + − ( 1) ( 1) ( 1) ( 1) (0)sin (0)cos ] k kk k G H k k ξ ψξ ψ − −− − − = ( +1) ( +1) +1 +1 [ (0)sin k k k k r G ξ ψ + ( +1) ( +1) ( ) ( ) +1 +1 (0)cos (1)sin k kk k H G k k ξ ψξ ψ − − () () +1(1)cos ] k k Hk ξ ψ (19) 式中, ( ) k ξ 为 k 界面上温度幅值与室外温度幅值的 比值, ( ) ( ) (o) k k A A ξ = 。 由于多层平壁内表面、外表面的谐波热幅值及 初相位为已知,该问题共有 2(n−1)个未知量: (1) ξ 、 (2) ξ L ( ) k ξ 、 ( 1) n ξ − 以及 (1) ψ 、 (2) ψ L ( ) k ψ L ( 1) n ψ − , 在墙体的(n−1)个界面上可以根据式(18)、式(19)列 出 2(n−1)个方程,采用迭代法解方程组便可得到 2(n−1)个未知量的解析解。 3.3 第 k 层温度场及其平均温度 由式(11)得第 k 层的温度场: (o) ( , ) ( ) cos[ ( )] Tt A t kk k η χ = + η ω ϕ η (20) 式中: 2 2 () () () χ k kk η θη ϑη = + ; 1 ( ) ( ) tan ( ) k k k ϑ η ϕ η θ η − = ; () () () () ( ) ( )cos ( )sin k kk k θη ξ η ψ ξ η ψ kk k = −+ E F ( 1) ( 1) ( 1) ( 1) (1 )cos (1 )sin k kk k E F k k ξ η ψ ξ ηψ − −− − − −− () () () () ( ) ( )sin ( )cos k kk k ϑη ξ η ψ ξ η ψ kk k =++ E F ( 1) ( 1) ( 1) ( 1) (1 )sin (1 )cos k kk k E F k k ξ ηψ ξ η ψ − −− − − +− 第 k 层平均温度为: 1 (o) 0 ( ) ( , )d cos[ ] Tt T t A t kk k k == + η η χ ω ϕ ∫ (21) 式中: 1 2 2 2 k kk k χ θ ϑ φ = + ; 1 tan k k k ϑ ϕ θ − = ; () () () () cos sin k k kk θ ςξ ψ ζξ ψ kk k =++ ( 1) ( 1) ( 1) ( 1) cos sin k k kk k k ςξ ψ ζξ ψ − − −− + () () () () sin cos kk k k ϑ ςξ ψ ζξ ψ kk k =− + ( 1) ( 1) ( 1) ( 1) sin cos kk k k k k ςξ ψ ζξ ψ −− − − − (1) (0) ς kk k = − H H ; (1) (0) ζ kk k = − G G 。 4 考虑空气对流换热时多层墙的 温度场 4.1 考虑室内空气对流换热时墙内表面温度 假设室内空气余弦谐波热幅值为 (i) A 、初相位 为 (i) ψ ,室内空气与墙内侧换热系数为αi 。对于第 三类边界条件下多层墙的传热,可以将墙的表面空 气边界层看成是多层墙的一层(如图 4),该层只有热 阻没有热容。多层墙内侧空气层内外两侧表面温度 和热流有如下关系[14]: (0) (i) i (0) (i) 1 () () 1 () () 0 1 T t Tt q t qt α ⎧⎪ ⎫ ⎧⎫ ⎪ ⎪⎪ − ⎨ ⎬ ⎨⎬ = ⎩ ⎭ ⎩⎭ ⎪ ⎪ ⎪⎪ (22) 式中: (0) T t( ) 、 (0) q t( ) 分别为室内空气层在 0 界面 上的温度和热流; (i) T t( ) 、 (i) q t( ) 分别为室内空气 层在 i 界面上的温度和热流。 由式(12),第 1 层在 0 界面热流为: (0) 1 qtq t ( ) (0, ) = = (o) (1) (1) (1) (1) 11 1 − −− rA G H {[ (0)cos (0)sin ξ ψξ ψ (0) (0) (0) (0) 1 1 ξ ψξ ψ ω GH t (1)cos (1)sin ]cos( ) + − (1) (1) (1) (1) 1 1 [ (0)sin (0)cos ξ ψξ ψ G H + − (0) (0) (0) (0) 1 1 ξ ψξ ψ GH t (1)sin (1)cos ]sin( )} − ω (23) 由式(22)、式(23),得: (0) (i) (i) (0) i i i 1 1 T t T t q t Tt q t () () () () () α α = − =− (0) (o) (i) (i) (1) 1 1 i ( ) cos [ (0) r TtA G ξψ ξ α ⎧ = +⋅ ⎨ ⎩ (1) (1) (1) (0) 1 1 cos (0)sin (1) ψξ ψξ − −⋅ H G (0) (0) (0) 1 cos sin (1)] cos( ) ψξ ψ ω H t ⎫ + − ⎬ ⎭ (o) (i) (i) (1) (1) 1 1 i sin [ (0)sin r A G ξψ ξ ψ α ⎧ ⎨ + + ⎩ (1) (1) (0) (0) 1 1 ξ ψξ ψ H G (0)cos (1)sin − − (0) (0) 1 ξ ψ H t (1)cos ] sin( ) ω ⎫ ⎬ ⎭ (24) 由式(11),并注意 1 E (0) 0 = , 1F (0) 0 = , 1 E (1) = 1, 1F (1) 0 = ,第 1 层在 0 界面上的温度: (0) 1 T tTt (0, ) (0, ) = = (0) (0) (0) A tt (cos cos( ) sin sin( )) ψ ω − ψ ω (25) 图 4 室内空气层 Fig.4 Air layer in indoor 由基本假设,0 界面上除了热流相等外,温度

198 也应相等。由式(24、式(25,得: H(0)sincos(ar)- cosG(0)cos H,(0)sin(G(1)cos) sin-()sin 5 )sinH,】=5 cosw0 (26 H()cosmG (0)sinv(-) sinG)sin H(0)cosy-]sin(ar) (30) H(0)cos)G(1)sin(o) 由式(1),并注意E(O)=0, Fn(0)=0 H(1)cos])sin(o) 27 E()=1,Fn)=0,第n层在n界面上的温度: 4,2考虑室外空气对流换热时墙外表面温度 T0=T,)= 若室外空气谐波热幅值为、初相位为 Aw(cos wm)cos()-sinw sin()(31】 w),室外空气与墙外侧换热系数为位。多层墙外 由基本假设,n界面上除了热流相等外,温度 侧空气层(图5)内外两侧表面温度和热流有如下关 也应相等。由式(30、式(31),得: 系 cosw)-{L5G,(cosy() (T(]1 r (28 H (1)siny()G (0)cos()+ H (0)sini]=)cosu(m)(32) 式中:T()、g)分别为室内空气层在n界面 上的温度和热流:T()、g()分别为室内空气 如vn-25G.0my4 层在。界面上的温度和热流 (mH(1)cosy(m)-g(n-G (0)siny(n-1)_ n-2- H(0)cos]=(m)sinw()(33) 由于多层墙内外空气的谐波热作用为己知,该 问题共有2(+2)个未知量:0、50、52)… 10 5…5-、5以及o、、2…y w-)、w),这里补充了多层墙内外空气层的4 个方程式(26)、式(27)、式(32、式(33),用选代法 或MATLAB程序解方程组便可得到多层培第三类 yer in 边界条件时的温度场的解析解。 由式(12,第n层n界面热流为: qm(t)=q(Lt)=-r4G(1)cos() 5算例:谐波热作用下外墙外保温 H(1)sin(m-G(0)cos-1)+ 墙体的温度场分析 H(0)sinw]cos(r)- 某墙体采用重砂浆砌筑的240mm厚烧结页岩 [G (1)sinH(1)cosy(m) 多孔砖墙:干密度A,=1400kg/m3、导热系数1= -G(0)sinwn-1)- 0.58W7m·K)、比热容c=1.05k/kg·K)、导温系 H(0)cos]sin(x) (29) 数a=0.000395m2h,该墙采用聚苯板保温层:干 由式28、式(29,得: 密度A=30kgm、导热系数=0.042Wm·K) T()=T(t)+- 比热容c=1.38kJg·K)、导温系数F 0.001014mh。可以用以上方法计算得到在不同保 温层厚度δ时外保温墙体温度场和平均温度随时间 (cosG(cosy 变化规律,如图6一图8所示。从图6~图8中可少以 H(1)sinwim)-gG(0)cosy)+ 看出: 1994-2015Chin Academic Jour al Electronic Publishing House.All ight http://www.cnki.net
198 工 程 力 学 也应相等。由式(24)、式(25),得: (i) (i) (1) (1) 1 1 i cos [ (0)cos r ξψ ξ ψ G α + − (1) (1) (0) (0) 1 1 ξ ψξ ψ H G (0)sin (1)cos − + (0) (0) (0) (0) 1 ξψ ξ ψ sin (1)] cos H = (26) (i) (i) (1) (1) 1 1 i sin [ (0)sin r ξψ ξ ψ G α + + (1) (1) (0) (0) 1 1 ξ ψξ ψ H G (0)cos (1)sin − − (0) (0) (0) (0) 1 ξ ψξψ H (1)cos ] sin = (27) 4.2 考虑室外空气对流换热时墙外表面温度 若室外空气谐波热幅值为 (o) A 、初相位为 (o) ψ ,室外空气与墙外侧换热系数为αo 。多层墙外 侧空气层(图 5)内外两侧表面温度和热流有如下关 系[14]: (o) ( ) o (o) ( ) 1 () () 1 () () 0 1 n n Tt Tt qt qt α ⎧⎫ ⎧⎫ ⎪⎪ ⎪⎪ − ⎨⎬ ⎨⎬ = ⎪⎪ ⎪⎪ ⎩⎭ ⎩⎭ (28) 式中: ( ) ( ) n T t 、 ( ) ( ) n q t 分别为室内空气层在 n 界面 上的温度和热流; (o) T t( )、 (o) q t( )分别为室内空气 层在 o 界面上的温度和热流。 图 5 室外空气层 Fig.5 Air layer in outdoor 由式(12),第 n 层 n 界面热流为: ( ) (o) ( ) ( ) ( ) (1, ) {[ (1)cos n nn nn n q t q t rA G = =− − ξ ψ ( ) ( ) ( 1) ( 1) (1)sin (0)cos n nn n H G n n ξ ψξ ψ − − − + ( 1) ( 1) (0)sin ]cos( ) n n H t n ξ ψω − − − () () () () [ (1)sin (1)cos n nn n G H n n ξ ψξ ψ + − ( 1) ( 1) (0)sin n n Gn ξ ψ − − − ( 1) ( 1) (0)cos ]sin( )} n n H t n ξ ψ ω − − (29) 由式(28)、式(29),得: ( ) (o) (o) (o) ( ) o o 1 1 () () () () () n n T tTt qtT t qt α α =+ =+ ( ) (o) (o) ( ) ( ) o ( ) cos [ (1)cos n nn n n r TtA G ψξ ψ α ⎧ =− − ⎨ ⎩ ( ) ( ) ( 1) ( 1) (1)sin (0)cos n nn n H G n n ξ ψξ ψ − − − + ( 1) ( 1) (0)sin ] cos( ) n n H t n ξ ψω − − ⎫ ⎬ − ⎭ (o) (o) ( ) ( ) o sin [ (1)sin n n n n r A G ψξ ψ α ⎧ ⎨ − + ⎩ ( ) ( ) ( 1) ( 1) (1)cos (0)sin n nn n H G n n ξ ψξ ψ − − − − ( 1) ( 1) (0)cos ] sin( ) n n H t n ξ ψ ω − − ⎫ ⎬ ⎭ (30) 由 式 (11) ,并注意 (0) 0 En = , (0) 0 Fn = , (1) 1 En = , (1) 0 Fn = ,第 n 层在 n 界面上的温度: ( ) ( ) (1, ) n TtTt = = n () () () (cos cos( ) sin sin( )) nn n A tt ψ ω − ψ ω (31) 由基本假设,n 界面上除了热流相等外,温度 也应相等。由式(30)、式(31),得: (o) ( ) ( ) o cos {[ (1)cos n n n n r ψξ ψ G α − − ( ) ( ) ( 1) ( 1) (1)sin (0)cos n nn n H G n n ξ ψξ ψ − − − + ( 1) ( 1) ( ) ( ) (0)sin ] cos n n nn Hn ξ ψ ξψ − − = (32) (o) ( ) ( ) o sin [ (1)sin n n n n r ψξ ψ G α − + ( ) ( ) ( 1) ( 1) (1)cos (0)sin n nn n H G n n ξ ψξ ψ − − − − ( 1) ( 1) ( ) ( ) (0)cos ] sin n n nn Hn ξ ψ ξψ − − = (33) 由于多层墙内外空气的谐波热作用为已知,该 问题共有 2(n+2)个未知量: (0) ξ 、 (1) ξ 、 (2) ξ L ( ) k ξ L ( 1) n ξ − 、 ( ) n ξ 以及 (0) ψ 、 (1) ψ 、 (2) ψ L ( ) k ψ L ( 1) n ψ − 、 ( ) n ψ ,这里补充了多层墙内外空气层的 4 个方程式(26)、式(27)、式(32)、式(33),用迭代法 或 MATLAB 程序解方程组便可得到多层墙第三类 边界条件时的温度场的解析解。 5 算例:谐波热作用下外墙外保温 墙体的温度场分析 某墙体采用重砂浆砌筑的 240mm 厚烧结页岩 多孔砖墙:干密度 3 0 ρ =1400kg/m 、导热系数λ = 0.58W/(m·K)、比热容c = 1.05kJ/(kg·K)、导温系 数 a = 0.000395 m 2 /h,该墙采用聚苯板保温层:干 密度 3 0 ρ = 30kg/m 、导热系数 λ= 0.042W/(m·K)、 比热容 c=1.38kJ/(kg·K) 、导温系数 a= 0.001014m2 /h。可以用以上方法计算得到在不同保 温层厚度 δ 时外保温墙体温度场和平均温度随时间 变化规律,如图 6~图 8 所示。从图 6~图 8 中可以 看出:
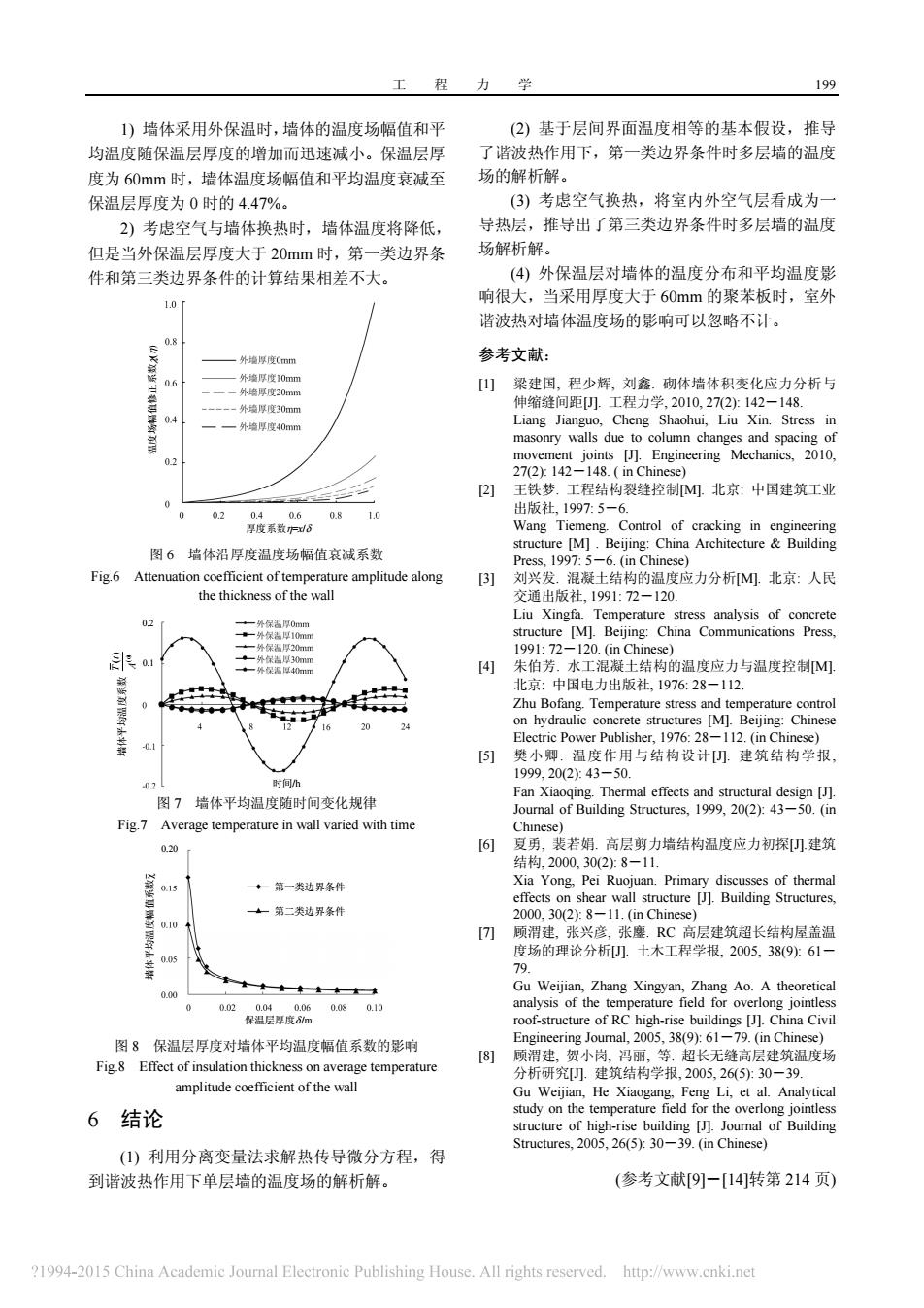
程 力 19 )墙体采用外保温时,墙体的温度场幅值和 (2)基于层间界面温度相等的基本假设,推导 均温度随保温层厚度的增加而迅速减小。保温层月 了谐波热作用下,第一类边界条件时多层墙的温度 度为60mm时,墙体温度场幅值和平均温度衰减至 场的解析解。 保温层厚度为0时的447%。 (3)若虑空气换热,将室内外空气层看成为 2)考虑空气与培体换热时,墙体温度将降低 导热层,推导出了第三类边界条件时多层墙的温度 但是当外保温层厚度大于20mm时,第一类边界条 场解析解 件和第三类边界条件的计算结果相差不大。 (④外保温层对墙体的温度分布和平均温度影 响很大,当采用厚度大于60mm的聚苯板时,室外 谐波热对培体温度场的影可以忽略不计。 参考文献: 山梁建国 0 21 王铁梦.工程结构裂缝控制M.北京:中国建筑工业 出版社1975一6 ntrol o 图6墙体沿厚度温度场幅值衰诚系数 刘兴发 混凝士结构的温度应力分析M北京:人民 交通出 99:72 02 工混凝土结构的温度应力与温度控制M 煲小卿。温度作用与结构设计建筑结构学报 haue Suure 19 al effects and Fig.7 vith time [6 复勇,装若娟。高层剪力墙结构温度应力初探)建筑 of th ·一第一类边界条件 Pei Ru ·一第二类边界条什 00.3021g-11 项渭建,张兴彦,张鏖.RC高层建筑超长结构屋盖温 度场的理论分析0土木工程学报,205,389外61 000 dings China Civil 图8保温层厚度对墙体平均温度幅值系数的影响 胃建,贺小岗 招 Fig.Effect of insulation thickness on average temperature 长无缝高层建筑温度场 研究建 5,2653 amplitude coefficient of the wall 6结论 Structures.2005.26(5):30-39.(in Chinese) ()利用分离变量法求解热传导微分方程,得 到谐波热作用下单层墙的温度场的解析解 (参考文献[9-[14转第214页) 1994-2015 China Academic Joural Eleetronic Publishing House.All rights reserved. http://www.cnki.net
工 程 力 学 199 1) 墙体采用外保温时,墙体的温度场幅值和平 均温度随保温层厚度的增加而迅速减小。保温层厚 度为 60mm 时,墙体温度场幅值和平均温度衰减至 保温层厚度为 0 时的 4.47%。 2) 考虑空气与墙体换热时,墙体温度将降低, 但是当外保温层厚度大于 20mm 时,第一类边界条 件和第三类边界条件的计算结果相差不大。 图 6 墙体沿厚度温度场幅值衰减系数 Fig.6 Attenuation coefficient of temperature amplitude along the thickness of the wall 图 7 墙体平均温度随时间变化规律 Fig.7 Average temperature in wall varied with time 图 8 保温层厚度对墙体平均温度幅值系数的影响 Fig.8 Effect of insulation thickness on average temperature amplitude coefficient of the wall 6 结论 (1) 利用分离变量法求解热传导微分方程,得 到谐波热作用下单层墙的温度场的解析解。 (2) 基于层间界面温度相等的基本假设,推导 了谐波热作用下,第一类边界条件时多层墙的温度 场的解析解。 (3) 考虑空气换热,将室内外空气层看成为一 导热层,推导出了第三类边界条件时多层墙的温度 场解析解。 (4) 外保温层对墙体的温度分布和平均温度影 响很大,当采用厚度大于 60mm 的聚苯板时,室外 谐波热对墙体温度场的影响可以忽略不计。 参考文献: [1] 梁建国, 程少辉, 刘鑫. 砌体墙体积变化应力分析与 伸缩缝间距[J]. 工程力学, 2010, 27(2): 142―148. Liang Jianguo, Cheng Shaohui, Liu Xin. Stress in masonry walls due to column changes and spacing of movement joints [J]. Engineering Mechanics, 2010, 27(2): 142―148. ( in Chinese) [2] 王铁梦. 工程结构裂缝控制[M]. 北京: 中国建筑工业 出版社, 1997: 5―6. Wang Tiemeng. Control of cracking in engineering structure [M] . Beijing: China Architecture & Building Press, 1997: 5―6. (in Chinese) [3] 刘兴发. 混凝土结构的温度应力分析[M]. 北京: 人民 交通出版社, 1991: 72―120. Liu Xingfa. Temperature stress analysis of concrete structure [M]. Beijing: China Communications Press, 1991: 72―120. (in Chinese) [4] 朱伯芳. 水工混凝土结构的温度应力与温度控制[M]. 北京: 中国电力出版社, 1976: 28―112. Zhu Bofang. Temperature stress and temperature control on hydraulic concrete structures [M]. Beijing: Chinese Electric Power Publisher, 1976: 28―112. (in Chinese) [5] 樊小卿. 温度作用与结构设计[J]. 建筑结构学报, 1999, 20(2): 43―50. Fan Xiaoqing. Thermal effects and structural design [J]. Journal of Building Structures, 1999, 20(2): 43―50. (in Chinese) [6] 夏勇, 裴若娟. 高层剪力墙结构温度应力初探[J].建筑 结构, 2000, 30(2): 8―11. Xia Yong, Pei Ruojuan. Primary discusses of thermal effects on shear wall structure [J]. Building Structures, 2000, 30(2): 8―11. (in Chinese) [7] 顾渭建, 张兴彦, 张鏖. RC 高层建筑超长结构屋盖温 度场的理论分析[J]. 土木工程学报, 2005, 38(9): 61― 79. Gu Weijian, Zhang Xingyan, Zhang Ao. A theoretical analysis of the temperature field for overlong jointless roof-structure of RC high-rise buildings [J]. China Civil Engineering Journal, 2005, 38(9): 61―79. (in Chinese) [8] 顾渭建, 贺小岗, 冯丽, 等. 超长无缝高层建筑温度场 分析研究[J]. 建筑结构学报, 2005, 26(5): 30―39. Gu Weijian, He Xiaogang, Feng Li, et al. Analytical study on the temperature field for the overlong jointless structure of high-rise building [J]. Journal of Building Structures, 2005, 26(5): 30―39. (in Chinese) (参考文献[9]―[14]转第 214 页) 0.20 第一类边界条件 第二类边界条件 保温层厚度δ /m 墙体平均温度幅值系数- χ 厚度系数η=x/δ 温度场幅值修正系数χ(η) 时间/h 墙体平均温度系数 ( ) (o) T t A 0.1 0.2 墙体平均温度系数 ( ) (o) T t A

214 力 学 1-T ac0-四sme, Di=c sh() G D=sinb() a-hoe+sme》, .co()-() Da=cosh(). Tasin() Xco)o-uXcwM(k)-cx 4(- g2. a流92 + 五面-2-边 TTu-TuT (上接第199页) Joumal of Building Suructures,0,5(6):9-8.(in Ai Bing.Yuan Mingzhao.Temperature field's numeric Building Structures,1995,2(4)4-48.(in Tu Chuanjing.Shen Luochan,Wu Zijing.Heat [10 伟良, 叶甲边道 [MjingHigher Education Pres19 3陈沛森,曹叔维,郭建谁.空调负荷计算理论与方法 577-581. M上海:向济大字出版社,19然7 ucture Joural of Zhejiang University (Engineering Science). 为.建筑用护结构的温 业出版社1986 度场数值模拟)建筑结构学报, 2004.25(6):93-9% 1994-2015 China Academic Journal Eleetronic Publishing House.All rights reserved.http:/www.enki.net
214 工 程 力 学 T T 33 22 = , 34 1 sinh( ) (1 ) 4 z T kz G k μ = − − , 41 ( cosh( ) sinh( )) 1 G T k kz kz kz μ = + − , 42 1 [ cosh( ) (1 2 )sinh( )] 1 2 k T kz kz kz μ μ = −− − , 3 43 sinh( ) 1 G T k z kz μ = − , T T 44 11 = , 11 D kz = cosh( ) , 12 sinh( ) kz D Gk = , 21 D Gk kz = sinh( ) , 22 D kz = cosh( ) , 2 2 2 22 [2(1 2 )(cosh( ) cos( )) sinh( )] [4(1 )(cosh( ) cos( )) sinh( )] 4 (1 )( ) s s s a s k kz z kz kz kz z kz kz p h k μγ μγ γ μ γ − − + +− − + = − + , 2 2 2 22 [2 (cos( ) cosh( )) sinh( )] [2(1 )(cosh( ) cos( )) sinh( )] 2 (1 )( ) s s s b s k z kz kz kz kz z kz kz p h k μγ μ γ γ μ γ − + +− − + = − − + , 2 2 2 22 ( cosh( ) sinh( )) 2 sin( ) ( cosh( ) sinh( )) 4 (1 )( ) s s s c s k kz kz kz k z kz kz kz p kh k γγ γ μ γ −− + + = − − + , 3 2 2 2 22 [ cosh( ) (1 2 )sinh( )] { [ cosh( ) (3 2 )sinh( )] 2sin( )[ (1 ) ]} 2 (1 )( ) s ss s d s k kz kz kz k kz kz kz z k p h k μ γ μ γ γ μ μγ μ γ +− + + − − −− = − + , 2 2 1 2 cosh( ) cos( ) 2 (1 ) s a s kz z q h k μ γ μ γ − − = − + , 2 2 1 2 sinh( ) sin( ) 2 (1 ) s s b s k kz z q h k μ γ γ μ γ − + = − + , 11 23 42 22 43 13 22 41 21 42 2 12 21 43 41 23 1 ( )( ) a T TT TT T TT TT T T k TT TT ⎡ ⎤ −+ − = + ⎢ ⎥ ⎣ ⎦ − %% %% %% %% %% %% , 11 43 13 41 2 21 43 41 23 1 b TT TT T k TT TT − = − % % %% %% , 11 23 13 21 13 41 11 43 2 21 43 41 23 1( ) ( ) d c a T T T T p T T T T pb T p k TT TT ⎡ − +− ⎤ = + ⎢ ⎥ ⎣ − ⎦ %% %% % % %% %% , 11 2 21 1 d ab D T qq k D ⎛ ⎞ = − ⎜ ⎟ ⎝ ⎠ % % 。 (上接第 199 页) [9] 艾兵, 原明昭. 房屋结构在日照作用下温度场的数值 计算[J]. 建筑结构, 1995, 25(4): 46―48. Ai Bing, Yuan Mingzhao. Temperature field’s numeric calculation on building structure affect by solar radiation [J]. Building Structures, 1995, 25(4): 46 ― 48. (in Chinese) [10] 金伟良, 叶甲淳, 邹道勤. 考虑太阳辐射作用的砌体 结构的温度场[J]. 浙江大学学报(工学版), 2002, 36(5): 577―581. Jin Weiliang, Ye Jiachun, Zou Daoqin. Temperature field of m asonry structure considering solar radiation [J]. Journal of Zhejiang University (Engineering Science), 2002, 36(5): 577―581. (in Chinese) [11] 李红梅, 金伟良, 叶甲淳, 王有为. 建筑围护结构的温 度场数值模拟[J]. 建筑结构学报, 2004, 25(6): 93―98. Li Hongmei, Jin Weiliang, Ye Jiachun, Wang Youwei. Temperature field simulation of building envelopes [J]. Journal of Building Structures, 2004, 25(6): 93―98. (in Chinese) [12] 屠传经, 沈珞婵, 吴子静. 热传导[M]. 北京: 高等教 育出版社, 1992: 169―179. Tu Chuanjing, Shen Luochan, Wu Zijing. Heat conduction [M]. Beijing: Higher Education Press, 1992: 169―179. (in Chinese) [13] 陈沛霖, 曹叔维, 郭建雄. 空调负荷计算理论与方法 [M]. 上海: 同济大学出版社, 1987. Chen Peilin, Cao Shuwei, Guo Jianxiong. Air conditioning load calculation theory and methods [M]. Shanghai: Tongji University Press, 1987. (in Chinese) [14] 彦启森, 赵庆珠. 建筑热过程[M]. 北京: 中国建筑工 业出版社, 1986. Yan Qisen, Zhao Qingzhu. Building thermal processes [M]. Beijing: China Architecture & Building Press, 1986. (in Chinese)