《高等传热学》课程教学资源（文献资料）隧道地源热泵供热系统加热段隔热层厚度及热负荷计算.pdf_大学文库

岩石力学与工程学报 Vol.31 No.4 Chinese Journal of Rock Mechanics and Engineering p7,201 隧道地源热泵供热系统加热段隔热层厚度及热负荷计算张国柱，夏才初，孙猛，邹一川，刘婷（1.同济大学地下建筑与工程系。上海20092：2.博济大学岩士及地下工程教有部原点实验室，上海200092 摘要：为解决寒区隧道冻害问愿，首次将地源热泵供热系统应用于内蒙古博牙高速林场隧道中。系统由取热段、加热段、热泵和分、集水管路组成。加热段位于隧道洞口处，由位于二村和保温隔热层之间的供热管对隧道进行如热。将复杂的隧道加热段热传导问题转化为便于求解的圆形复合介质热传导问题，利用有限积分变换法获得其温度场解析解。利用考虑隔热层材料造价和耗能的经济计算模型，计算分析隧道全寿命周期30a的隔热层厚度和供热负荷。计算结果表明：随着隔热层厚度的增加，隔热层材料费呈线性增如，供热消耗的电费呈递减趋势，材料费与电费之和呈递减趋势。建议林场隧道保温隔热层厚度取8cm,年供热负荷取580M山m己，关键词：隧道工程：地源热泵供热系统：隔热层厚度：供热负荷中图分类号：U45 文献标识码：A 文章编号：1000-69152012)04-0746-08 CALCULATION OF INSULATION LAYER THICKNESS AND HEATING LOAD OF HEATING SECTION OF TUNNEL HEATING SYSTEM USING HEAT PUMP ZHANG Guozhu,XIA Caichu,SUN Meng. ZOU Yichuan,LIU Ting (1.Depart 2 Shanghat 200092.China) Abstract:In order to solve the freezing damage problem of tunnel in cold region,an innovative heating system- tunnel heating system using heat pump was introduced for the first time to Linchang tunnel in Inner Mongolia Autonomous Region of China.Tunnel heating system consists of heating section,absorbing section,heat pump, collector and distributor line.The heating section is at the portal of tunnel and heated by the heating pipes located between secondary lining and insulation layer.The heat conduction of heating section is transformed to the heat conduction ofc osite edium in the cvlindrical co stem.Its analytical solution obtained using ethod The ng load is tical solution u nditior erent ir lav thickness ad npu Is to of insulatio ial a ete Linch el in Inne onomous Region of Chin .Result that the en ergy costs decrease with the ing insulatio layer thickn ess:the cost of insu n material increases linearly with the increasing nsulation layer thickr ss.Total cost,which is sum of insula ion material cost and energy cost,decreases with th ncreasing insulation yer thickness.The optimum insulation layer thickness is obtained to be8cm:the yearly heating load is 580 MJ/m Key words:tunnelling engineering:heating system using heat pump:insulation layer thickness:heating load 收裤日期：2011-12-01：日期：2012-01-0 从事成道及地下建筑工程、能源地下工程方面的研究

第 31 卷第 4 期岩石力学与工程学报 Vol.31 No.4 2012 年 4 月 Chinese Journal of Rock Mechanics and Engineering April，2012 收稿日期：2011–12–01；修回日期：2012–01–06 基金项目：国家自然科学基金资助项目(50878150)；交通部西部交通建设科技项目(2009318822047)；长江学者和创新团队发展计划(IRT1029) 作者简介：张国柱(1982–)，男，2005 年毕业于吉林大学岩土工程专业，现为博士研究生，主要从事隧道及地下建筑工程、能源地下工程方面的研究工作。E-mail：zhangguozhu240101@163.com 隧道地源热泵供热系统加热段隔热层厚度及热负荷计算张国柱，夏才初，孙猛，邹一川，刘婷 (1. 同济大学地下建筑与工程系，上海 200092；2. 同济大学岩土及地下工程教育部重点实验室，上海 200092) 摘要：为解决寒区隧道冻害问题，首次将地源热泵供热系统应用于内蒙古博牙高速林场隧道中。系统由取热段、加热段、热泵和分、集水管路组成。加热段位于隧道洞口处，由位于二衬和保温隔热层之间的供热管对隧道进行加热。将复杂的隧道加热段热传导问题转化为便于求解的圆形复合介质热传导问题，利用有限积分变换法获得其温度场解析解。利用考虑隔热层材料造价和耗能的经济计算模型，计算分析隧道全寿命周期 30 a 的隔热层厚度和供热负荷。计算结果表明：随着隔热层厚度的增加，隔热层材料费呈线性增加，供热消耗的电费呈递减趋势，材料费与电费之和呈递减趋势。建议林场隧道保温隔热层厚度取 8 cm，年供热负荷取 580 MJ/m2 。关键词：隧道工程；地源热泵供热系统；隔热层厚度；供热负荷中图分类号：U 45 文献标识码：A 文章编号：1000–6915(2012)04–0746–08 CALCULATION OF INSULATION LAYER THICKNESS AND HEATING LOAD OF HEATING SECTION OF TUNNEL HEATING SYSTEM USING HEAT PUMP ZHANG Guozhu，XIA Caichu，SUN Meng，ZOU Yichuan，LIU Ting (1. Department of Geotechnical Engineering，Tongji University，Shanghai 200092，China；2. Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education，Tongji University，Shanghai 200092，China) Abstract：In order to solve the freezing damage problem of tunnel in cold region，an innovative heating system— tunnel heating system using heat pump was introduced for the first time to Linchang tunnel in Inner Mongolia Autonomous Region of China. Tunnel heating system consists of heating section，absorbing section，heat pump， collector and distributor line. The heating section is at the portal of tunnel and heated by the heating pipes located between secondary lining and insulation layer. The heat conduction of heating section is transformed to the heat conduction of composite medium in the cylindrical coordinate system. Its analytical solution was obtained using the finite integral transfer method. The yearly heating load is calculated by using the analytical solution under steady periodic conditions at different insulation layer thicknesses. These loads are used as inputs to an economic model including the cost of insulation material and the present value of energy consumption cost lifetime of 30 years of tunnel to determine the optimum insulation layer thickness. The investigation is carried out for Linchang tunnel in Inner Mongolia Autonomous Region of China. Results show that the energy costs decrease with the increasing insulation layer thickness；the cost of insulation material increases linearly with the increasing insulation layer thickness. Total cost，which is sum of insulation material cost and energy cost，decreases with the increasing insulation layer thickness. The optimum insulation layer thickness is obtained to be 8 cm；the yearly heating load is 580 MJ/m2 . Key words：tunnelling engineering；heating system using heat pump；insulation layer thickness；heating load

第31卷第4期张国柱等：隧道地源热泵供热系统加热段隔热层厚度及热负荷计算 ·747: 现有的建筑结构的研究成果对隧道并不适用。 1引言隧道加热段温度场非常复杂，不但要考虑地表和洞内气温双重低温作用的用岩相变，还需要考虑寒区隧道在冬季要面临冻害的威胁，我国76% 供热管作为线热源向隧道衬砌提供热量，又由于隧的寒区隧道都发生了不同程度的冻害破坏。利用电道加热段计算区域的不规则性，很难直接获得其解能和煤炭的隧道加热系统虽能永久根除隧道冻害析解但却增加了隧道的运行管理费用，并带来环境污染本文根据隧道温度场的影响范围，将加热段的等问题。H Brand等2-提出了采用地热能的球道热传导问题转化为圆形复合介质的热传导问题。利技术，即利用布置于隧道初衬和二衬之间的能源」用积分变化法求解圆形复合介质温度场解析解工布吸收围岩地温能，地源热泵将其提升后，用于用该解析解计算不同隔热层厚度下的隧道供暖热负隧道附近建筑供暖。H.Brand开展了采用地热能荷。并利用考虑隔热层材料造价和能源消耗费的经的隧道现场试验研究，该试验工程用6台地源热系济计算模型，计算分析依托工程林场隧道全寿命周将提取的地温能为附近一所学校供暖，能提供150 期30a的隔热层厚度和供暖负荷。 kW功率的热能，一个供暖季度可提供214MW.h 的能量。M.S.Islam等4研发了水平单U管道路加热段温度场加热系统，利用埋于隧道中部路面下1.2m处的水平单U管吸收围岩地温能，对隧道洞口段的路面加热，由于隧道洞内气温沿隧道轴线方向的温度变化该技术成功应用于Nanaori-Toge隧道，现场温度监梯度很小，隧道围岩在轴线方向发生的热传导可测表明，隧道洞口路面温度始终处于冰点以上，达以忽略，加热段温度场可按二维传热模型计算。隧到了预期效果。夏才初等在分析急结国外先讲技道实际断面形式为马蹄形，接近于圆形，为便于计术的基础上，提出了能源地下工程新概念，并对其算，计算檬型中的哮道断面按圆形考虑。应用前景做了详细论述。张国柱等提出了利用地隧道开挖对一定范用内围岩的原始温度场产生温能的寒区隧道地源热泵供热系统，并开展了岩土影响，在该范围内的围岩温度受洞内气温和地表气热响应试验。温双重作用，在该范围以外的围岩温府场仅受地表有关寒区隧道地源热泵型供热系统加热段隔热气温作用，不受隧道开挖的影响。在确定隧道温度层及热负荷计算方面的研究成果尚未见报道。建筑场影响范围边界处的温度T.(@,)后，加热段传热结构的隔热层优化己获得大量的研究成果)。但问题可转化为圆形复合介质的传热问题（见图1）。由于结构形式、模型边界及供热方式等方面的差别， 2.1计算影响边界处的温度T(日，) 八表 7八7 道温度场影响外边界 .n 转化图1隧道地源热系供热系统加热段二维传热模型 Fig Two-dimensional heat transfer model of heating section of tunnel heating system using heat pump

第 31 卷第 4 期张国柱等：隧道地源热泵供热系统加热段隔热层厚度及热负荷计算 • 747 • 1 引言寒区隧道在冬季要面临冻害的威胁，我国 76% 的寒区隧道都发生了不同程度的冻害破坏。利用电能和煤炭的隧道加热系统虽能永久根除隧道冻害，但却增加了隧道的运行管理费用，并带来环境污染等问题[1]。H. Brandl 等[2-3]提出了采用地热能的隧道技术，即利用布置于隧道初衬和二衬之间的能源土工布吸收围岩地温能，地源热泵将其提升后，用于隧道附近建筑供暖。H. Brandl[2]开展了采用地热能的隧道现场试验研究，该试验工程用 6 台地源热泵将提取的地温能为附近一所学校供暖，能提供 150 kW 功率的热能，一个供暖季度可提供 214 MW·h 的能量。M. S. Islam 等[4-5]研发了水平单 U 管道路加热系统，利用埋于隧道中部路面下 1.2 m 处的水平单 U 管吸收围岩地温能，对隧道洞口段的路面加热。该技术成功应用于 Nanaori-Toge 隧道，现场温度监测表明，隧道洞口路面温度始终处于冰点以上，达到了预期效果。夏才初等[6]在分析总结国外先进技术的基础上，提出了能源地下工程新概念，并对其应用前景做了详细论述。张国柱等[7]提出了利用地温能的寒区隧道地源热泵供热系统，并开展了岩土热响应试验。有关寒区隧道地源热泵型供热系统加热段隔热层及热负荷计算方面的研究成果尚未见报道。建筑结构的隔热层优化已获得大量的研究成果[8-11]。但由于结构形式、模型边界及供热方式等方面的差别，现有的建筑结构的研究成果对隧道并不适用。隧道加热段温度场非常复杂，不但要考虑地表和洞内气温双重低温作用的围岩相变，还需要考虑供热管作为线热源向隧道衬砌提供热量，又由于隧道加热段计算区域的不规则性，很难直接获得其解析解。本文根据隧道温度场的影响范围，将加热段的热传导问题转化为圆形复合介质的热传导问题。利用积分变化法求解圆形复合介质温度场解析解。利用该解析解计算不同隔热层厚度下的隧道供暖热负荷。并利用考虑隔热层材料造价和能源消耗费的经济计算模型，计算分析依托工程林场隧道全寿命周期 30 a 的隔热层厚度和供暖负荷。 2 加热段温度场由于隧道洞内气温沿隧道轴线方向的温度变化梯度很小[12]，隧道围岩在轴线方向发生的热传导可以忽略，加热段温度场可按二维传热模型计算。隧道实际断面形式为马蹄形，接近于圆形，为便于计算，计算模型中的隧道断面按圆形考虑。隧道开挖对一定范围内围岩的原始温度场产生影响，在该范围内的围岩温度受洞内气温和地表气温双重作用，在该范围以外的围岩温度场仅受地表气温作用，不受隧道开挖的影响。在确定隧道温度场影响范围边界处的温度 3d T t ( ) ，后，加热段传热问题可转化为圆形复合介质的传热问题(见图 1)。 2.1 计算影响边界处的温度 3d T t ( ) ，图 1 隧道地源热泵供热系统加热段二维传热模型 Fig.1 Two-dimensional heat transfer model of heating section of tunnel heating system using heat pump 地表二衬供热管空气层隔热层转化隧道温度场影响外边界 T3d(，t) r0 r1 r2 rT

• 748 • 岩石力学与工程学报 2012年土层原始温度场由 3 个区域组成，如图 2 所示。第一个区域为冻结区，第二个区域为混合区，第三个区域为未冻区。图 2 半无限大体温度场计算模型 Fig.2 Heat transfer model of semi-infinite medium temperature field 第一，二，三区的传热方程分别如下： 2 1d 1d 2 1 1d 1 ( ) ( ) (0 ( )) T T z t z t z Xt z t       ，， ≤≤ (1) 2 2d 2d 2 1 2d 1 ( ) ( ) ( ( ) ( )) T T z t z t X t z Xt z t       ，，＜＜ (2) 2 3d 3d 2 3 1 ( ) ( ) ( () ) T T z t z t Xt z z t       ，， ≤ (3) 边界条件： 1d s 1d s min (0 ) (0 ) T t hT t hT z    ，， (4) 1d 1 2d 1 m T Xt t T Xt t T ( () ) ( () ) ，，   (5) 1d 2d 1d 1 2d 1 ( () ) ( () ) T T k Xt t k Xt t z z      ，， (6) 2d 3d f T Xt t T Xt t T ( () ) ( () ) ，，   (7) 2d 3d 2d 3 f d () ( () ) ( () ) d T T X t k Xt t k Xt t L z z t       ，， (8) 初始条件： d 0 ( 0) Tz T i ，  (i = 1，2，3) (9) 式中： 1d Tzt ( ) ，为冻结区的温度； 2d T zt ( ) ，为混合区的温度； 3d Tzt ( ) ，为未冻结区的温度； 1 X t( ) 为冰水混合移动边界；X t( )为相变移动边界；Lf 为相变潜热； s h 为地表和大气的对流换热系数；Tm 为水完全转化为冰的温度；Tf 为产生相变的温度；Tmin 为地表温度，为确保隔热层厚度满足防冻要求，取最低月平均气温作为地表温度；T0 为原始地温。 J. M. Mckenzie 等[13]给出了上述传热问题的温度场解析解： 1d 1d m s s erf[ / (2 )] ( )( ) erf ( ) z t Tzt T T T   ，    (10) 4d 2d m f f 1d 4d erf[ / (2 )] erf ( ) ( )( ) erf ( ) erf ( / ) z t T zt T T T           ， (11) 3 3d f 0 0 4d 3 erfc[ / (2 )] ( )( ) erfc( / ) z t Tzt T T T    ，    (12) 1d c ， 2d c 和 3 c 分别为冻结区、混合区和未冻区的热容量，计算式分别如下： 1d w w wres i i wres r r c cS c S c         (1 ) (1 ) (13) 2d w w w i i w r r c cS c S c         (1 ) (1 ) (14) 3 ww rr cc c     (1 ) (15) 式中： 为岩体孔隙率； w S 为水的饱和度； wres S 为水的残余饱和度； r ，  w 和 i 分别为岩石、水和冰的密度； r c ， wc 和 i c 分别为岩石、水和冰的比热容。 1d k ， 2d k 和 3d k 分别为冻结区、混合区和未冻区的导热系数，计算式分别如下： 1d w wres w wres w k kS k S k       (1 ) (1 ) (16) 2d w w i w r k kS k S k        (1 ) (1 ) (17) 3w r kk k    (1 )  (18) 式中： r k ， wk 和 i k 分别为岩石、水和冰的导热系数。 1d ，3 和4d 分别为冻结区、混合区和未冻区的热扩散系数，计算式分别如下： 1d 1d 1d k c   (19) 3 3 3 k c   (20) 2 4d 2 rf f m (1 ) ( ) k c L TT        (21) 其中， w wres w r r (1 ) (1 )   S         (22) 对于任意时间 t，在区域 1 0 () ≤ ≤ 内，岩体 z X t 的温度场为T1d ，边界 1 X t( ) 由下式计算： 1—冻结区 3—未冻区 2—冰水混合区 Tf Tm Tmin X1(t) X(t)

第 31 卷第 4 期张国柱等：隧道地源热泵供热系统加热段隔热层厚度及热负荷计算 • 749 • 1 1d Xt t () 2    (23) 在区域 1 X t z Xt () () ＜ ≤ 内，岩体的温度场为T2d ，边界 X t( )由下式计算： 4d Xt t () 2    (24) 参数 和 由下列方程组确定： 2 1d 4d 2 1d 4d m s (1 ) m f 2d 1d 1d 4d 1d 4d m f 2d 3 (1 ) 0 f3 4 1d 4d 4d 3 e erf ( ) erf ( ) erf ( ) e erf ( ) erf ( ) erfc( ) d T T T T k k T T k T Tk                                             (25) 为充分利用隧道围岩的地热，隧道洞身位于未冻区内。若隧道埋深和温度场影响半径 T r 已知，根据式(12)即可计算隧道温度场影响边界处的温度场： 3 3d f 0 0 4d 3 erfc[ / (2 )] ( )( ) erfc( / ) R t T t TT T     ，   (26) 其中， R (1 sin ) Rd r   T  (27) 式中： R d 为隧道温度场影响边界最高点距离地表的距离。为满足隧道供暖所需热负荷并便于计算，取    / 2 处，冻深最大时的温度作为隧道外边界温度，即 R 30 3d 3d f 0 0 4d 3 erfc[ / (2 )] () ( ) erfc( / ) d t T t T TT T     ，   (28) 其中， 2 0 0 4d 1 4 z t          (29) 式中： 0 z 为该地区土层的标准冻深。 2.2 圆形复合介质传热方程在确定了影响边界处的温度后，加热段的传热问题转化为圆形复合介质传热问题，传热方程如下：隔热层温度场： 1 1 1 1 1 () () T T r t rr t t rr r                 ，，，， 2 1 2 2 1 1 () ( ) T qr t r t r k       ，，，， (30) 隧道二衬温度场： 2 2 2 1 1 () () T T r t rr t t rr r                 ，，，， 2 2 2 2 1 ( ) T r t r     ，， (31) 围岩温度场： 3 3 3 1 1 () () T T r t rr t t rr r                 ，，，， 2 3 2 2 1 ( ) T r t r     ，， (32) 隧道内边界为衬砌与洞内气体发生的对流热传导边界： 1 1 0 10 ( ) ( ) () T k r t hT r t hf t r       ，，，， (33) 隧道外边界为恒温边界： 3 3d ( ) Tr t T T，，  (34) 周期边界条件： ( 0 ) ( 2 ) Tr t Tr t i i ，，，，   (35) ( 0 ) ( 2 ) T T i i rt r t         ，，，， (36) 连续条件： 1 ( )( ) Tr t T r t ii i i ，，，，     (i = 1，2) (37) 1 1 () () i i ii i i T T k r tk r t r r          ，，，， (i = 1，2)(38) 初始条件： ( 0) ( ) Tr fr i i ，，，    (i = 1，2，3； 0 T r rr ≤ ≤ ) (39) 式中：T1 为隔热层温度场；T2 为二衬温度场；T3为隧道围岩温度场；i 和 i k (i = 1，2，3)分别为第 i 区的热扩散系数和导热系数； ( ) i f r，为各层初始  温度场；f ( )t 为隧道洞内气体温度场；qr t ( ) ，，为  隧道供热热负荷，由下式计算： 1 ( ) () ( ) ( ) n hh j j qr t q t r r      ，，    (40) 式中： ( ) h q t 为每延米供热管的供热量， hr 和 j 为供热管所在的位置，n 为隧道供热段横断面内供交换的数量。 2.3 方程求解利用叠加原理[14]将圆形复合介质的传热方程进行如下分解：

• 750 • 岩石力学与工程学报 2012年 ( )( )( ) Tr t r r t i ii ，，，，，       (41) 函数 ( ) i  r，和  ( ) i   r t ，，是下列问题的解。函数 ( ) i  r，与原问题具有相同定义域，无热源的  稳态热传导问题的解： 1 1 () () i i i r rr t rr r                (42) 边界条件： 1 1 0 10 R k r h r hT () () r       (43a) 3 3d ( ) T  r T  (43b) 连续条件： 1 () () ii i i   r r   (i = 1，2) (43c) 1 1 () () i i i ii i k rk r r r          (i = 1，2) (43d) 式中：TR 为隧道洞内气体温度的代表温度，借鉴建筑结构热负荷的计算方法，取每月第 15 天的洞内气温作为本月的代表温度。夏才初等[15]获得了上述方程的解析解。函数 ( ) i   r t ，，与原问题具有相同定义域，有热源，但具有齐次边界条件的非稳态热传导问题的解。隔热层温度场： 1 1 1 1 1 () () r t rr t t rr r                   ，，，， 2 1 2 2 1 1 () ( ) qr t r t r k        ，，，， (44a) 隧道二衬温度场： 2 2 2 1 1 () () r t rr t t rr r                   ，，，， 2 2 2 2 1 ( ) r t r      ，， (44b) 围岩温度场： 3 3 3 1 1 () () r t rr t t rr r                   ，，，， 2 3 2 2 1 ( ) r t r      ，， (44c) 边界条件： 1 1 0 10 k r thr t ( ) ( )0 r        ，，，， (44d) 3 ( )0 T   r t ，，  (44e) ( 0 ) ( 2 ) i i   rt r t ，，，，   (44f) ( 0 ) ( 2 ) i i rt r t           ，，，， (44g) 连续条件： 1 ( )( ) ii i i    rt rt ，，，，   (i = 1，2) (44h) 1 1 () () i i ii i i k r tk r t r r            ，，，， (i = 1，2) (44i) 初始条件： ( 0) ( ) i i  r fr ，，，    (i = 1，2，3； 0 d r rr ≤ ≤ ) (44j) S. Singh 等[16]获得了上述问题的求解方法，限于篇幅，此处不再赘述。加热段温度场的解析解如下： R 3d 0 0 1 11 ( ) () () () () ( ) ( )cos( ) i r r op mpc i p imp p mp op mp T r t TFr T Gr t t Rr Rr m N N                 ，， 1 1 ( ) ( )sin( ) r mps imp m p mp t Rr m N         (45) 其中， 2 2 1 1 1 1 00 1 0 0 ( ) ( )e ( )e d mp mp t t r p h mp h i t rR r g            (46) 2 2 1 1 1 1 1 0 ( ) ( )e ( )e d mp mp t t r mpc h mp h imc t rR r g            (47) 2 2 1 1 1 1 1 0 ( ) ( )e ( )e d mp mp t t r mps h mp h ims t rR r g            (48) 0 ( ) ( ) 2 h i q t g t    (49) 1 ( ) cos( ) ( ) imc h g t m qt     (50) 1 ( ) sin( ) ( ) ims h g t m qt     (51) 1 2 1 1 1 d i i n r i mp imp mp r i i i k N rR r r                   (52) 式中： ( ) h q t 为每延米供热管的供热量， hr 为供热管所在处的极坐标， ( ) R r imp 为第 i 层传热介质在不含热源的齐次边界下热传导方程的特征函数，1mp 为第 1 层传热介质在不含热源的齐次边界下热传导方程的特征值，n 为复合传热介质的层数。 3 隧道供暖热负荷隧道供暖热负荷应确保位于隧道二衬外侧的隧道排水系统不发生冻结，始终处于通畅状态。为确

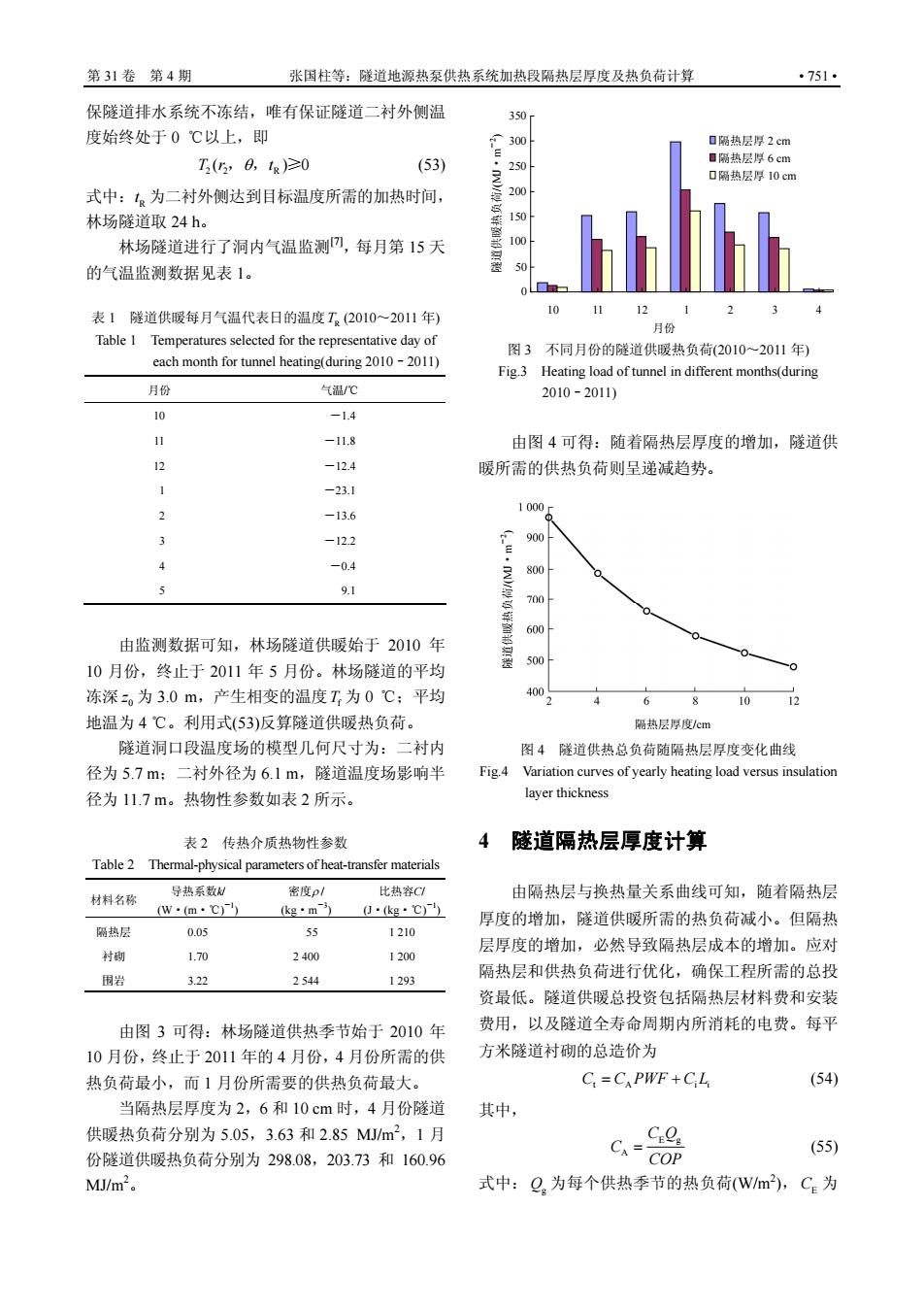
第31卷第4期张国住等：隧道地源热泵供热系统加热段隔热层厚度及热负荷计算 ·751 保隧道排水系统不冻结，唯有保证隧道二衬外侧温度始终处于0℃以上，即 T,a,t)≥0 (53) 式中：为二衬外侧达到目标温度所需的加热时间， 0隔热层厚10 200 林场隧道取24h。林场隧道进行了洞内气温监测网，每月第15天的气温监测数据见表1。表1隧道供暖每月气温代表日的温度工，(2010一201年 10 图3不同月份的隧道供暖热负荷(2010~2011年) Fig.3 load of tunnel in differ 月份气温/℃ 2010-2011) 10 -14 11 由图4可得：随着隔热层厚度的增加，隧道供 -124 暖所需的供热负荷则呈递减趋势。 -23.1 -136 -122 -04 9.1 由监测数据可知，林场隧道供暖始于2010年 10月份，终止于2011年5月份。林场隧道的平均冻深为3.0m, 产生相变的温度T为0℃：平均 8 10 地温为4℃。利用式(53)反算隧道供暖热负荷。层热层根府大游道洞口段温度场的模型几何尺、寸为：二衬内图4隧道供热总负荷随隔热层厚度变化曲线径为5.7m: 衬外径为6.1m,隧道温度场影响半 sofyearl 径为11.7m。热物性参数如表2所示。 layer 表2传热介质热物性参数 4隧道隔热层厚度计算 Table 2 Thermal-physical parameters of heat-transfer materials 材料名称导热系数U 密度p 比热容由隔热层与换热量关系曲线可知，随若隔热房 w·m·c kg·m 肠热层 0.05 1210 厚度的增加，隧道供暖所需的热负荷减小。但隔热 55 层厚度的增加，必然导致隔热层成本的增加。应对村南 1.70 2400 1200 围岩 322 2544 1293 隔热层和供热负荷进行优化，确保工程所需的总投资最低。隧道供暖总投资包括隔热层材料费和安装由图3可得：林场隧道供热季节始于2010年费用，以及隧道全寿命周期内所消耗的电费。每平 10月份，终止于2011年的4月份，4月份所需的供方米隧道衬砌的总造价为热负荷最小，而1月份所需要的供热负荷最大 C.=C PWF+CL (54) 当隔热层厚度为2,6和10cm时，4月份隧道其中供暖热负荷分别为5.05,3.63和2.85M/m2,1月 Co 份隧道供暖热负荷分别为298.08,203.73和160,96 CA=COP (55) M/m2。式中：Q为每个供热季节的热负荷(wm),C为

第 31 卷第 4 期张国柱等：隧道地源热泵供热系统加热段隔热层厚度及热负荷计算 • 751 • 保隧道排水系统不冻结，唯有保证隧道二衬外侧温度始终处于 0 ℃以上，即 22 R Tr t ( )0 ，， ≥  (53) 式中： Rt 为二衬外侧达到目标温度所需的加热时间，林场隧道取 24 h。林场隧道进行了洞内气温监测[7]，每月第 15 天的气温监测数据见表 1。表 1 隧道供暖每月气温代表日的温度TR (2010～2011 年) Table 1 Temperatures selected for the representative day of each month for tunnel heating(during 2010–2011) 月份气温/℃ 10 －1.4 11 －11.8 12 －12.4 1 －23.1 2 －13.6 3 －12.2 4 －0.4 5 9.1 由监测数据可知，林场隧道供暖始于 2010 年 10 月份，终止于 2011 年 5 月份。林场隧道的平均冻深 0 z 为 3.0 m，产生相变的温度Tf 为 0 ℃；平均地温为 4 ℃。利用式(53)反算隧道供暖热负荷。隧道洞口段温度场的模型几何尺寸为：二衬内径为 5.7 m；二衬外径为 6.1 m，隧道温度场影响半径为 11.7 m。热物性参数如表 2 所示。表 2 传热介质热物性参数 Table 2 Thermal-physical parameters of heat-transfer materials 材料名称导热系数k/ (W·(m·℃) －1 ) 密度 / (kg·m－3 ) 比热容C/ (J·(kg·℃) －1 ) 隔热层 0.05 55 1 210 衬砌 1.70 2 400 1 200 围岩 3.22 2 544 1 293 由图 3 可得：林场隧道供热季节始于 2010 年 10 月份，终止于 2011 年的 4 月份，4 月份所需的供热负荷最小，而 1 月份所需要的供热负荷最大。当隔热层厚度为 2，6 和 10 cm 时，4 月份隧道供暖热负荷分别为 5.05，3.63 和 2.85 MJ/m2 ，1 月份隧道供暖热负荷分别为 298.08，203.73 和 160.96 MJ/m2 。月份图 3 不同月份的隧道供暖热负荷(2010～2011 年) Fig.3 Heating load of tunnel in different months(during 2010–2011) 由图 4 可得：随着隔热层厚度的增加，隧道供暖所需的供热负荷则呈递减趋势。隔热层厚度/cm 图 4 隧道供热总负荷随隔热层厚度变化曲线 Fig.4 Variation curves of yearly heating load versus insulation layer thickness 4 隧道隔热层厚度计算由隔热层与换热量关系曲线可知，随着隔热层厚度的增加，隧道供暖所需的热负荷减小。但隔热层厚度的增加，必然导致隔热层成本的增加。应对隔热层和供热负荷进行优化，确保工程所需的总投资最低。隧道供暖总投资包括隔热层材料费和安装费用，以及隧道全寿命周期内所消耗的电费。每平方米隧道衬砌的总造价为 C C PWF C L t A ii   (54) 其中， E g A C Q C COP  (55) 式中：Qg 为每个供热季节的热负荷(W/m2 )， CE 为隧道供暖热负荷/(MJ·m－2) 隧道供暖热负荷/(MJ·m－2) 0 50 100 150 200 250 300 350 10 11 12 1 2 3 4 隔热层厚 2 cm 隔热层厚 6 cm 隔热层厚 10 cm

752· 岩石力学与工程学报 2012年电费元kW·h),COP为能效比，C为每立方米过增加隔热层厚府隆低工程造价，效里并不明品隔热材料的费用（元m.L为瓶热材料的厚府(m) 如果继续增加隔热层厚度，势必会侵占二衬建筑界 C,为每供暖季节消耗的电费（元m2·a,PW 限，需扩大隧道开挖尺寸，从而增加总工程造价。现时价值因数所以，建议林场隧道加热段保温隔热层厚度取8 隧道供暖总投资应考虑全寿命周期内的现时价 m,年供热负荷取580MJm2。由于供热管位于保值因数PW吓，现时价值因数PWF与通货膨胀率g 温隔热层与二村之间，空气又具有良好的隔热效果和银行利率1有关。现时价值因数PWF计算公式如加热段的隔热层厚度取6cm,并在隔热层与二衬之下：间填充2cm厚的空气层。 PWF=(+ry-1 r1+r) (56) 5结论其中根据隧道温度场的影响范围，将加热段的热传导问题转化为圆形复合介质的热传导问题。利用积 r=1+8 (g) (57 分变化法求得其解析解。利用该解析解计算不同隔热层厚度下的隧道供暖热负荷。利用考虑隔热层材 1i (i=8) 料造价和能源消耗费的经济计算模型，计算依托工程林场隧道全寿命周期30a的隔热层厚度和供暖负式中：N为全寿命周期。荷。初步得到了如下结论：利用式(54)计算加热段隔热层和供热负荷，计 (1)林场隧道供热季节始于10月份，终止于下算所需参数见表3，计算分析结果见图5。一年的4月份，4月份所需的供热负荷最小，而1 月份所需要的供热负荷最大。随若隔热层厚度的增加，隧道供暖所需的供热负荷则呈递减趋势 (②)随着隔热层厚度的增加，隧道供暖所需电地源热泵隔热材料的费呈递减趋势，隔热层材料费呈线性增加，工程总造价呈递减趋势。当隔热层厚度大于8cm时 0.6 40 4000 4 30 通过增加隔热层厚度降低工程造价，效果并不 -0e (3)林场隧道保温隔热层厚度取8cm,年供热 1200 负荷为580MJm2。由于供热管位于保温隔热层与二衬之间，空气又具有良好的隔热效果，因此供热 2400 段的隔热层厚度取6cm,在隔热层与二衬之间填充 160 2cm厚的空气层。参考文献(References): 6 8 1012 山夏才初。张国柱，曹诗定，等寒区公路碰通防冻保暖技木及其发隔热层界度西图5工程造价随隔热层厚度变化曲线展趋势C2009年全国公路能道学术会议论文集、兰州：B Fig.5 009 13-19.(XIA Caichu,ZHANG,CAOShiding,etal Variation curves of cost with insulation layer thickness 图5表明，随着隔热层厚度的增加，隧道供暖 ngd 所需电费呈递减趋势：隔热层材料费呈线性增加： Road Tunnel in 2009.Lanzhou:Is.n].2009:13-19.(in Chinese) 工程总造价呈递减趋势。当隔热层厚度大于8cm 2BRANDL H.Energy fourdations and other thermo-active grou 时，曲线趋于平缓。当隔热层厚度大于8cm时，通

• 752 • 岩石力学与工程学报 2012年电费(元/(kW·h))，COP 为能效比，Ci 为每立方米隔热材料的费用(元/m3 )， Li 为隔热材料的厚度(m)， CA 为每供暖季节消耗的电费(元/(m2 ·a))，PWF 为现时价值因数[11]。隧道供暖总投资应考虑全寿命周期内的现时价值因数 PWF，现时价值因数 PWF 与通货膨胀率 g 和银行利率 i 有关。现时价值因数 PWF 计算公式如下： (1 ) 1 (1 ) N N r PWF r r     (56) 其中， () 1 () 1 1 ( ) 1 i g i g g g i r ig g i g i                 ＞＜ (57) 式中：N 为全寿命周期。利用式(54)计算加热段隔热层和供热负荷，计算所需参数见表 3，计算分析结果见图 5。表 3 计算所需参数 Table 3 The parameters used in calculations 电费 CE / (元·(kW·h) －1 ) 地源热泵能效比 COP 隔热材料的费用 Ci / (元·m－3 ) 通货膨胀率 g/% 银行利率 i/% 全寿命周期 N/a 0.6 4.0 4 000 4 5 30 隔热层厚度/cm 图 5 工程造价随隔热层厚度变化曲线 Fig.5 Variation curves of cost with insulation layer thickness 图 5 表明，随着隔热层厚度的增加，隧道供暖所需电费呈递减趋势；隔热层材料费呈线性增加；工程总造价呈递减趋势。当隔热层厚度大于 8 cm 时，曲线趋于平缓。当隔热层厚度大于 8 cm 时，通过增加隔热层厚度降低工程造价，效果并不明显。如果继续增加隔热层厚度，势必会侵占二衬建筑界限，需扩大隧道开挖尺寸，从而增加总工程造价。所以，建议林场隧道加热段保温隔热层厚度取 8 cm，年供热负荷取 580 MJ/m2 。由于供热管位于保温隔热层与二衬之间，空气又具有良好的隔热效果，加热段的隔热层厚度取 6 cm，并在隔热层与二衬之间填充 2 cm 厚的空气层。 5 结论根据隧道温度场的影响范围，将加热段的热传导问题转化为圆形复合介质的热传导问题。利用积分变化法求得其解析解。利用该解析解计算不同隔热层厚度下的隧道供暖热负荷。利用考虑隔热层材料造价和能源消耗费的经济计算模型，计算依托工程林场隧道全寿命周期 30 a 的隔热层厚度和供暖负荷。初步得到了如下结论： (1) 林场隧道供热季节始于 10 月份，终止于下一年的 4 月份，4 月份所需的供热负荷最小，而 1 月份所需要的供热负荷最大。随着隔热层厚度的增加，隧道供暖所需的供热负荷则呈递减趋势。 (2) 随着隔热层厚度的增加，隧道供暖所需电费呈递减趋势，隔热层材料费呈线性增加，工程总造价呈递减趋势。当隔热层厚度大于 8 cm 时，通过增加隔热层厚度降低工程造价，效果并不明显。 (3) 林场隧道保温隔热层厚度取 8 cm，年供热负荷为 580 MJ/m2 。由于供热管位于保温隔热层与二衬之间，空气又具有良好的隔热效果，因此供热段的隔热层厚度取 6 cm，在隔热层与二衬之间填充 2 cm 厚的空气层。参考文献(References)： [1] 夏才初，张国柱，曹诗定，等. 寒区公路隧道防冻保暖技术及其发展趋势[C]// 2009 年全国公路隧道学术会议论文集. 兰州：[s.n.]， 2009：13–19.(XIA Caichu，ZHANG Guozhu，CAO Shiding，et al. Antifreeze and warmth retention technology and developing trend of road tunnel in frigid areas[C]// Proceedings of National Conference on Road Tunnel in 2009. Lanzhou：[s.n.]，2009：13–19.(in Chinese)) [2] BRANDL H. Energy foundations and other thermo-active ground structures[J]. Geotechnique，2006，56(2)：81–122. 材料费电费总造价工程造价/(元· m－2)

第31卷第4期张国柱等：隧道地源热泵供热系统加热段隔热层厚度及热负荷计算 ·753 [3]ADAM D.MARKIEWICZ R Energy from earth-coupled structures. [10]DAOUAS N.HASSEN Z.AISSIA H B.Analytical periodie solution foundation.tunnel and sewersl Geotechnique.2009.593):229- for the study of thermal performance and optimum insulation thickness 236. of building walls in Tunisia].Applied Thermal Engineering.2010. 4]IALAM M S.FUKUHARA T.WATANABE H.et al.Horizontal 30(4:319-326. U-tube road heating system using tunnel ground hea Joumal of [11]SISMAN N.KAHYAE,ARAS N,et al.Determination ofoptimum Snow Engineering of Japan,06.22(3):229-234. insulation thicknesses of the exteral walls and rooffceiling)fo [5]IALAM M S.FUKUHARA T.WATANABE H.Simplified heat Turkey's different degree-day regions Energy Policy.2007 transfer model of horizontal U-tube(HUT)system Joumal of Snov 35(10:5151-5153 Engineering of Japan.007.23(3):232-239 以孙文吴.寒区特长公路隧道抗防冻对策研究[硕士学位论文] 夏才初，曹诗定，王伟.能源地下工程的概念、应用与前绿展塑即成都：西南交通大学，2005.SUN Wenhao..Study 地下空间与I程学报，2009,53419-424(A Caichu,CA0 antifreezing strategies of extra-long highway tunnel in cold area[M.S. Shiding,WANG Wei.An introduction to energy geotechnical Thesis][D]Chongqing:Southwest Jiaotong University,2005 (n Chinese)) engineering and its application and prospect Chinese Joumal of [13]MCKENZIE J M,VOSS CI,SIEGEL D I.Groundwater flow with Underground Space and Engineering,2009.5(3):419-424.(in energy transport and water-ice phase change:numerical simulations. Chinese)) benchmarks,and application to freezing in peat bogs Advances in )张国柱，夏才初，马绪光，等.寒区隧道地源热泵型供热系统岩土 Water Resources,2007.30:966-983. 热响应试验)岩石力学与工程学报，2012,31：9-105. [14]OZISIK MN.Heat conduction[M].New York:John Wiley and Sons. (ZHANG Guozhu,XIA Caichu.MA Xuguang.et al.Rock-soil thermal 1ne,1980:136-137. response test of tunnel heating system using heat pump in cold 【)夏才初，张国柱，肖素光.考忠衬砌和隔热层的寒区隧道温度场解 regChinese oual of Rock Mechanics and Engineering.012. 析解)岩石力学与工程学报，2010,299：1767-1773(X1A 31):99-105.(nChinese) Caichu.ZHANG.Guozhu.XIAO Suguang.Analytical solution to 8OZEL M.Thermal performance and optimum insulation thickness of temperature fields of tunne in cold region considering liningand building walls with different structure Therma insulation layer Chinese Joumal of Rock Mechanics and Engineering,201l,3117/8:3854-386 Engineering.2010,9():1767-1773.(in Chinese)) OZEL M.PIHTILI K.Investigation of the most suitable location of [16]SINGHS.JAIN PK.UDDIN R.Finite integral transform method to insulation plyingon budinooffrommaximum lod leveling solve asymmetric heat conduction ina multilayer annulus with point of view[].Building and Environment,2007.42(6):2 360- time-dependent boundary conditions].Nuclear Engineering and 2368. Design,20Il,241(0:144-154

第 31 卷第 4 期张国柱等：隧道地源热泵供热系统加热段隔热层厚度及热负荷计算 • 753 • [3] ADAM D，MARKIEWICZ R. Energy from earth-coupled structures， foundation，tunnel and sewers[J]. Geotechnique，2009，59(3)：229– 236. [4] IALAM M S，FUKUHARA T，WATANABE H，et al. Horizontal U-tube road heating system using tunnel ground heat[J]. Journal of Snow Engineering of Japan，2006，22(3)：229–234. [5] IALAM M S，FUKUHARA T，WATANABE H. Simplified heat transfer model of horizontal U-tube(HUT) system[J]. Journal of Snow Engineering of Japan，2007，23(3)：232–239. [6] 夏才初，曹诗定，王伟. 能源地下工程的概念、应用与前景展望[J]. 地下空间与工程学报，2009，5(3)：419–424.(XIA Caichu，CAO Shiding，WANG Wei. An introduction to energy geotechnical engineering and its application and prospect[J]. Chinese Journal of Underground Space and Engineering，2009，5(3)：419–424.(in Chinese)) [7] 张国柱，夏才初，马绪光，等. 寒区隧道地源热泵型供热系统岩土热响应试验[J]. 岩石力学与工程学报，2012，31(1)：99–105. (ZHANG Guozhu，XIA Caichu，MA Xuguang，et al. Rock-soil thermal response test of tunnel heating system using heat pump in cold region[J]. Chinese Journal of Rock Mechanics and Engineering，2012， 31(1)：99–105.(in Chinese)) [8] OZEL M. Thermal performance and optimum insulation thickness of building walls with different structure materials[J]. Applied Thermal Engineering，2011，31(17/18)：3 854–3 863. [9] OZEL M，PIHTILI K. Investigation of the most suitable location of insulation applying on building roof from maximum load leveling point of view[J]. Building and Environment，2007，42(6)：2 360– 2 368. [10] DAOUAS N，HASSEN Z，AISSIA H B. Analytical periodic solution for the study of thermal performance and optimum insulation thickness of building walls in Tunisia[J]. Applied Thermal Engineering，2010， 30(4)：319–326. [11] SISMAN N，KAHYA E，ARAS N，et al. Determination of optimum insulation thicknesses of the external walls and roof(ceiling) for Turkeys different degree-day regions[J]. Energy Policy，2007， 35(10)：5 151–5 155. [12] 孙文昊. 寒区特长公路隧道抗防冻对策研究[硕士学位论文][D]. 成都：西南交通大学，2005.(SUN Wenhao. Study on frostresisting and antifreezing strategies of extra-long highway tunnel in cold area[M. S. Thesis][D]. Chongqing：Southwest Jiaotong University，2005.(in Chinese)) [13] MCKENZIE J M，VOSS C I，SIEGEL D I. Groundwater flow with energy transport and water-ice phase change：numerical simulations， benchmarks, and application to freezing in peat bogs[J]. Advances in Water Resources，2007，30：966–983. [14] OZISIK M N. Heat conduction[M]. New York：John Wiley and Sons， Inc.，1980：136–137. [15] 夏才初，张国柱，肖素光. 考虑衬砌和隔热层的寒区隧道温度场解析解[J]. 岩石力学与工程学报，2010，29(9)：1 767–1 773.(XIA Caichu，ZHANG，Guozhu，XIAO Suguang. Analytical solution to temperature fields of tunnel in cold region considering lining and insulation layer[J]. Chinese Journal of Rock Mechanics and Engineering，2010，29(9)：1 767–1 773.(in Chinese)) [16] SINGH S，JAIN P K，UDDIN R. Finite integral transform method to solve asymmetric heat conduction in a multilayer annulus with time-dependent boundary conditions[J]. Nuclear Engineering and Design，2011，241(1)：144–154