
高等传热学 目录 一、一维相变导热 二、固相热容可忽略时的相变导热 三、相变问题的精确解 四、求解相变问题的积分解
高 等 传 热 学 目 录 一、一维相变导热 二、固相热容可忽略时的相变导热 三、相变问题的精确解 四、求解相变问题的积分解

高等传热学 相变:物质集态或组织结构的变化 固液相变过程:液相由于冷却而凝固成固相,或固相由于 受热而变成液相的熔化过程 物理现象:冰层的形成、大地的融冰、钢锭及铸件的凝固、 食品的冷冻 相变导热过程特点: 。固、液两相之间存在着移动的分界面或分界区域,直至 相变过程结束 ●在相变过程中,有相变潜热的释放(凝固)或吸收(熔化)
高 等 传 热 学 相变:物质集态或组织结构的变化 固液相变过程:液相由于冷却而凝固成固相,或固相由于 受热而变成液相的熔化过程 物理现象:冰层的形成、大地的融冰、钢锭及铸件的凝固、 食品的冷冻 相变导热过程特点: ⚫ 固、液两相之间存在着移动的分界面或分界区域,直至 相变过程结束 ⚫ 在相变过程中,有相变潜热的释放(凝固)或吸收(熔化)

高等传热学 一、 一维相变导热 固体 液体 受 热 液体 固体 ·界面推进方向 一界面推进方向 s(r) s(r) 一维相变过程示意图 (a)凝固 (6)熔化
高 等 传 热 学 一、一维相变导热 一维相变过程示意图 (a)凝固 (b)熔化

高等传热学 固相区温度:ts(t) 液相区温度:t() 固相区导热微分方程: 液相区导热微分方程: 02t 0t, 02tr Ot 0≤x≤s(t) d元 =010s2 S()≤x≤L 相界面边界条件: 温度连续性条件:固液两相在界面处的温度相等,且等于相变状态 下的相变温度tp ts(x,t)=ti(x,t)=tp x=s(t) 能量平衡条件:导出控制容积的净热量等于凝固过程的放热量 股A股=p,Lg把 入股ata-2)=,lg照 (考虑液相区对流) dr
高 等 传 热 学 固相区温度:𝑡𝑠 (𝜏) 固相区导热微分方程: 𝜕𝑡𝑠 𝜕𝜏 = 𝛼𝑠 𝜕 2 𝑡𝑠 𝜕𝑠 2 0 ≤ 𝑥 ≤ 𝑠(𝜏) 液相区温度:𝑡𝑙 (𝜏) 液相区导热微分方程: 𝜕𝑡𝑙 𝜕𝜏 = 𝛼𝑙 𝜕 2 𝑡𝑙 𝜕𝑠 2 𝑠(𝜏) ≤ 𝑥 ≤ 𝐿 相界面边界条件: 温度连续性条件:固液两相在界面处的温度相等,且等于相变状态 下的相变温度𝒕𝒑 𝑡𝑠 𝑥, 𝜏 = 𝑡𝑙 𝑥, 𝜏 = 𝑡𝑝 𝑥= 𝑠(𝜏) 能量平衡条件:导出控制容积的净热量等于凝固过程的放热量 𝜆𝑠 𝜕𝑡𝑠 𝜕𝑥 -𝜆𝑙 𝜕𝑡𝑙 𝜕𝑥 = 𝜌𝑠𝐿 𝑑𝑠(𝜏) 𝑑𝜏 𝜆𝑠 𝜕𝑡𝑠 𝜕𝑥 -α(𝑡∞ − 𝑡𝑝) = 𝜌𝑠𝐿 𝑑𝑠(𝜏) 𝑑𝜏 (考虑液相区对流)

高等传热学 ts(x,t)=ti(x,T)=tp x=s(t) 取全导数 柴dx+ ax dr 0ts@+0t:0驰s@+ atL-0 ax dr Ot dx dt x=s(t) ds(①_ats/ar-_at/ar dt ats/ax atu/ax 票股=-p As atl/ot 股=p,l0 ats0t-psle1ax ats/0x λ50
高 等 传 热 学 𝑡𝑠 𝑥, 𝜏 = 𝑡𝑙 𝑥, 𝜏 = 𝑡𝑝 𝑥= 𝑠(𝜏) 取全导数 𝜕𝑡𝑠 𝜕𝑥 𝑑𝑥 + 𝜕𝑡𝑠 𝜕𝜏 𝑑𝜏 𝑥=𝑠(𝜏) + 𝜕𝑡𝑙 𝜕𝑥 𝑑𝑥 + 𝜕𝑡𝑙 𝜕𝜏 𝑑𝜏 𝑥=𝑠(𝜏) =0 𝜕𝑡𝑠 𝜕𝑥 𝑑𝑥 𝑑𝜏 + 𝜕𝑡𝑠 𝜕𝜏 𝑥=𝑠(𝜏) + 𝜕𝑡𝑙 𝜕𝑥 𝑑𝑥 𝑑𝜏 + 𝜕𝑡𝑙 𝜕𝜏 𝑥=𝑠(𝜏) =0 𝜕𝑡𝑠 𝜕𝑥 𝑑𝑠(𝜏) 𝑑𝜏 + 𝜕𝑡𝑠 𝜕𝜏 = 𝜕𝑡𝑙 𝜕𝑥 𝑑𝑠(𝜏) 𝑑𝜏 + 𝜕𝑡𝑙 𝜕𝜏 =0 𝑥 = 𝑠(𝜏) 𝑑𝑠(𝜏) 𝑑𝜏 =- 𝜕𝑡𝑠/𝜕𝜏 𝜕𝑡𝑠/𝜕𝑥 =− 𝜕𝑡𝑙/𝜕𝜏 𝜕𝑡𝑙/𝜕𝑥 𝜆𝑠 𝜕𝑡𝑠 𝜕𝑥 -𝜆𝑙 𝜕𝑡𝑙 𝜕𝑥 = 𝜌𝑠𝐿 𝑑𝑠(𝜏) 𝑑𝜏 𝜆𝑠 𝜕𝑡𝑠 𝜕𝑥 -𝜆𝑙 𝜕𝑡𝑙 𝜕𝑥 = −𝜌𝑠𝐿 𝜕𝑡𝑠/𝜕𝜏 𝜕𝑡𝑠/𝜕𝑥 =−𝜌𝑠𝐿 𝜕𝑡𝑙/𝜕𝜏 𝜕𝑡𝑙/𝜕𝑥
高等传热学 二、固相热容可忽略时的相变导热 湖水初始温度t(t:>tp) 9 x=0 湖面上环境温度t(to<tp) 冰层 s(r ·(x,x) 湖水与环境对流换热:1 湖水 冰层下湖水与冰层对流换热:2 如果在结冰过程中,由于冰温度的降 低放出的热量比相变潜热小得多,因 此,在湖水整个结冰过程中,可以忽 湖面上水的结冰过程 略冰层热容的作用。冰层中的温度分 布在任何时刻都是一条直线,但直线 的斜率随时间而变化
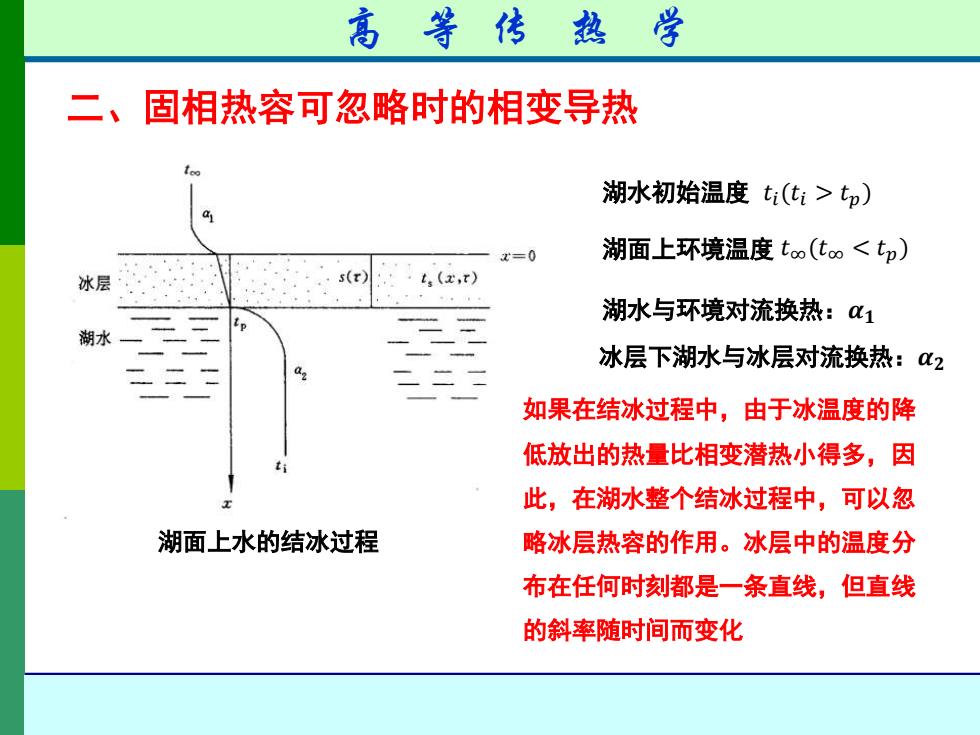
高 等 传 热 学 二、固相热容可忽略时的相变导热 湖面上水的结冰过程 湖水初始温度 𝑡𝑖 (𝑡𝑖 > 𝑡𝑝) 湖面上环境温度 𝑡∞(𝑡∞ < 𝑡𝑝) 湖水与环境对流换热:𝜶𝟏 如果在结冰过程中,由于冰温度的降 低放出的热量比相变潜热小得多,因 此,在湖水整个结冰过程中,可以忽 略冰层热容的作用。冰层中的温度分 布在任何时刻都是一条直线,但直线 的斜率随时间而变化 冰层下湖水与冰层对流换热:𝜶𝟐

高等传热学 冰层内温度场微分方程及定解条件 d2ts =0 tp-too dx2 ts(x,)=to+ -+s(t)/2s + Ots 一1s0x -an(t-t)x=0 a2=az(G-tp)+p3L9 +so/风, ts=tp x=s(t) 引入无量纲变量和参数 Ste=Cps(tp-too)/L asT s=41S/2s m ti-tp tp-too R=a2/a1 元=it2teo)-Ste·Fo PsLAs 1+5 ds tp-too z(d-t)+psL细 d版=1-mR(1+S) +5(t)/2s a1 5=0元=0
高 等 传 热 学 冰层内温度场微分方程及定解条件 𝑑 2 𝑡𝑠 𝑑𝑥 2 = 0 −𝜆𝑠 𝜕𝑡𝑠 𝜕𝑥 = 𝛼1 𝑡∞ − 𝑡𝑠 𝑥 = 0 𝑡𝑠 = 𝑡𝑝 𝑥 = 𝑠(𝜏) 𝑡𝑠 𝑥, 𝜏 = 𝑡∞ + 𝑡𝑝 − 𝑡∞ 1 𝛼1 + 𝑠(𝜏)/𝜆𝑠 1 𝛼1 + 𝑥 𝜆𝑠 𝑡𝑝−𝑡∞ 1 𝛼1 +𝑠(𝜏)/𝜆𝑠 =𝛼2 𝑡𝑖 − 𝑡𝑝 + 𝜌𝑠𝐿 𝑑𝑠(𝜏) 𝑑𝜏 引入无量纲变量和参数 𝑆𝑡𝑒 = 𝑐𝑝𝑠(𝑡𝑝 − 𝑡∞)/𝐿 𝐹𝑜 = 𝛼𝑠𝜏 𝜆𝑠 2 𝛼1 2 𝑠ҧ= 𝛼1𝑠/𝜆𝑠 𝑚 = 𝑡𝑖 − 𝑡𝑝 𝑡𝑝 − 𝑡∞ 𝑅 = 𝛼2/𝛼1 𝜏ҧ= 𝛼1 2 𝜏(𝑡𝑝−𝑡∞) 𝜌𝑠𝐿𝜆𝑠 =𝑆𝑡𝑒 ∙ 𝐹𝑜 𝑡𝑝−𝑡∞ 1 𝛼1 +𝑠(𝜏)/𝜆𝑠 =𝛼2 𝑡𝑖 − 𝑡𝑝 + 𝜌𝑠𝐿 𝑑𝑠(𝜏) 𝑑𝜏 𝑑𝜏ҧ= 1 + 𝑠ҧ 1 − 𝑚𝑅(1 + 𝑠ҧ) 𝑑𝑠ҧ 𝑠ҧ=0 𝜏ҧ=0

高等传热学 1+5 d元= ds 1-mR(1+ 元=§ 1n[1-mRs/(1-mR)] mR (mR)2 5=0元=0 3 1.6 mR=0 1.4 1.2 .0.2 2 4 0.4 0.65 0.6 0.4 0.8 0 2 0 3 冰层厚度随时间的变化
高 等 传 热 学 𝑑𝜏ҧ= 1 + 𝑠ҧ 1 − 𝑚𝑅(1 + 𝑠ҧ) 𝑑𝑠ҧ 𝑠ҧ=0 𝜏ҧ=0 𝜏ҧ=- 𝑠ҧ 𝑚𝑅 − ln[1−𝑚𝑅𝑠ҧ/(1−𝑚𝑅)] (𝑚𝑅) 2 冰层厚度随时间的变化

高等传热学 元→0∞ =1-mR_=(,-ta)-a2(-tp) mR az(ti-tp) 冰层只能生长到一定的厚度Smax=5max·三,此时冰层的上表面温度等于环境温 度,而冰层上表面与环境的对流散热等于湖水与冰层下表面的对流换热量 ●湖水的初始温度等于相变温度(t:=t,) 液相区域无热交换,mR=0(1+)d5=d元 5=-1+V1+2元 冰层厚度将随时间的推移而一直增大 ●mR=1 ai(tp-to)=az(ti-tp) 5max=0湖水不会结冰 ·湖水的初始温度等于相变温度(t:=t,)且湖面保持常温tw(tw<tp) 0-S-w) S() S()-队,w巧1/2冰层厚度按时间的平方根增加
高 等 传 热 学 𝜏ҧ→ ∞ 𝑠ҧ𝑚𝑎𝑥 = 1 − 𝑚𝑅 𝑚𝑅 = 𝛼1 𝑡𝑝 − 𝑡∞ − 𝛼2 𝑡𝑖 − 𝑡𝑝 𝛼2 𝑡𝑖 − 𝑡𝑝 冰层只能生长到一定的厚度𝑺𝒎𝒂𝒙 = 𝒔ത𝒎𝒂𝒙 ∙ 𝝀𝒔 𝜶𝟏 , 此时冰层的上表面温度等于环境温 度,而冰层上表面与环境的对流散热等于湖水与冰层下表面的对流换热量 ⚫ 湖水的初始温度等于相变温度(𝒕𝒊 = 𝒕𝒑) 液相区域无热交换,𝒎𝑹 = 𝟎 1 + 𝑠ҧ𝑑𝑠ҧ= 𝑑𝜏ҧ 𝑠ҧ= −1 + 1 + 2𝜏 冰层厚度将随时间的推移而一直增大 ⚫ 𝒎𝑹 = 𝟏 𝛼1 𝑡𝑝 − 𝑡∞ = 𝛼2 𝑡𝑖 − 𝑡𝑝 𝑠ҧ𝑚𝑎𝑥=0 湖水不会结冰 ⚫ 湖水的初始温度等于相变温度(𝒕𝒊 = 𝒕𝒑)且湖面保持常温𝒕𝒘(𝒕𝒘 < 𝒕𝒑) 𝑆 𝜏 𝑑𝑆 𝜏 𝑑𝜏 = 𝜆𝑠 𝜌𝐿 (𝑡𝑝 − 𝑡𝑤) 𝑆 𝜏 =[ 2𝜆𝑠 (𝑡𝑝−𝑡𝑤)𝜏 𝜌𝐿 ] 1/2 冰层厚度按时间的平方根增加

高等传热学 三、相变问题的精确解 半无限空间过冷液体的凝固过程 界 面 非常缓慢地冷却液体,则可 固体 把液体的温度降低到相变温 过冷液体 度以下,这一状态下的液体 t=却 t(x,r) 称为过冷液体。在过冷液体 到某一临界温度以后,液体 变会开始凝固,凝固时放出 的相变热会提高过冷液体的 温度 s(r) 半无限空间内过冷液体的凝固过程
高 等 传 热 学 三、相变问题的精确解 半无限空间过冷液体的凝固过程 半无限空间内过冷液体的凝固过程 非常缓慢地冷却液体,则可 把液体的温度降低到相变温 度以下,这一状态下的液体 称为过冷液体。在过冷液体 到某一临界温度以后,液体 变会开始凝固,凝固时放出 的相变热会提高过冷液体的 温度