
嘉著升别 JOURNAL七意来本L考羊UNIVERSTTY 学学 文音编号.1006-2467(2013)09-1367-05 无限大区域内四管冻结的稳态温度场解析解 胡向东,郭旺,张洛瑜 (同济大学地下建筑与工程系,岩土及地下工程教育部重点实验室,上海200092) 摘要:采用势函数叠加理论推导了4根冻结管以任意形式排列冻结时的稳态温废场解析解,得 出了4根冻结管以等间距直线、矩形和菱形等列时的稳态温度场特定解,并用热学数值模拟方法 对解析解进行验证,结果表明,解析解的计算结果与数值模拟结果校吻合 关键词:人工地层冻结法;冻结管,势函数:稳态:湿度场 中图分类号:TU311.4 文献标志码:A Analytical Solution of Steady State Temperature Field of Four Freezing Pipes in an Infinite Region HU Xiang-dong GUO Wang ZhANG Luovu atory of Geotechnical and Underground Engineering of Ministry of Education.Tongji University.Shanghai 00092.China) Abstract:Based on the potential superposition theory.this paper gives analytical solutions to steady state frozen temperature of four freezing pipes arranged at random.Particular solutions are derived for some par ticular arrangements.such as four freezing pipes with rectangle arrangement and rhombus arrangement Comparison of the analytical solutions with the numerical thermal analysis shows that the analytical solu tions are precise en ough. 在采用冻结法施工的过程中,冻土的力学性质 单管、单排和双排冻结管的冻土帷幕温度场计算方 及幕厚度等参数都依赖于冻结温度场的分布,因 多 3】 nge 获得了单排管温度场分布的计 此,冻结温度场的计算是人工冻结法理论研究的封 公式:Tobe等 和Kat0等 得出了多管等间距直 础。人工冻土温度场的计算方法主要有解析法、模扣 线形冻土推幕的温度场计算方法:笔者也曾对稳 法以及数值分析法.其中,解析法由于具有较好的可 态温度场的计算公式进行研究和完善. 党性而成为研家的重占。考皮人工地厚张结后期 姚而,在实际工理中,为处理,些特殊工和(如 冻土发展缓,其温度场接近于稳态导热温度场,故 需在某一部位进行冻结封水),通常采用布置4根 冻土状态可按稳态导热来求 解 结管的形式文献[ -5]中得到了4根冻结管以等间 基于稳态导热理论的冻 温度场” 距线排列时的总态品度场解析解,但针对4根 取得了进展.例如:Trupak和Bakholdin提出了 结管以其他形式(如矩形或菱形)排列的稳态温度场 数精日期:201212.0g 电话(Tel.):02165988771,Email:an 1994-2016 China Academic Joumal Electronie Publishing House.All rights reserved. http://www.cnki.net
第 卷 第 期 年 月 上 海 交 通 大 学 学 报 文 章 编 号 : 无 限大区 域 内 四 管冻 结 的 稳 态 温度 场解析解 胡 向 东 , 郭 旺 , 张 洛瑜 同 济 大学 地 下建 筑与 工 程 系 , 岩土 及地下 工 程教育 部重 点 实 验 室 , 上 海 摘 要 : 采 用 势 函 数 叠 加 理 论 推 导 了 根 冻 结 管 以 任 意 形 式 排 列 冻 结 时 的 稳 态 温 度 场 解 析 解 , 得 出 了 根 冻 结 管 以 等 间 距 直 线 、 矩 形 和 菱 形 等 排 列 时 的 稳 态 温 度 场 特 定 解 , 并 用 热 学 数值模 拟 方 法 对解 析 解进 行验 证 结 果表 明 , 解 析 解 的 计 算 结 果 与 数值 模拟 结 果 较吻 合 关 键 词 : 人 工 地层 冻 结 法 ; 冻 结 管 ; 势 函 数 ; 稳 态 ; 温 度 场 中 图 分 类 号 : 文 献 标 志 码 : , , : : ; ; ; ; 在采 用 冻结 法 施 工 的 过程 中 , 冻 土 的 力 学性 质 及 帷幕厚 度 等参 数 都 依赖 于 冻 结 温 度 场 的 分 布 , 因 此 , 冻结 温度 场 的 计 算 是 人 工冻 结 法 理论 研 究 的 基 础 人工 冻土 温度 场 的 计算 方法 主 要有 解 析 法 、 模拟 法 以 及数 值 分析 法 其 中 , 解析法 由 于 具有 较好 的 可 靠性 而成 为 研 究 的 重 点 考虑 到 人 工地 层 冻 结 后 期 冻土 发展 缓慢 , 其 温度 场接 近 于 稳 态 导 热 温度场 , 故 冻 土状 态 可 按 稳态 导 热 来求 解 基 于 稳 态 导热 理论 的 冻 土 温度 场解 析解 研 究 已 取 得 了 进 展 例 如 : 和 提 出 了 单管 、 单 排和 双排冻 结 管 的 冻 土 帷 幕 温度 场计 算 方 法 ; 等 也 获 得 了 单排 管 温 度场 分 布 的 计算 公式 ; 等 ⑷ 和 等 得 出 了 多 管 等 间 距 直 线形 冻土 帷幕 的 温 度 场 计算方 法 ; 笔者也 曾 对稳 态温 度 场 的 计算 公 式进 行研 究 和 完 善 然 而 , 在 实 际 工程 中 , 为 处 理 一 些 特 殊工 况 ( 如 需 在某 一 部 位进行 冻结 封水 ) , 通 常 采 用 布 置 根 冻 结 管 的 形式 文 献 中 得 到 了 根冻 结 管 以 等 间 距直线 排列 时 的 稳 态 温度 场 解 析 解 , 但 针 对 根 冻 结 管 以 其他形 式 ( 如 矩形 或菱 形 ) 排列 的 稳态 温 度场 收 稹 日 期 : 基 金 项 目 : 国 家 自 然 科 学 基 金 项 目 ( , 浙 江 省交 通 运 输 厅 科 技 计 划项 目 ( 资助 作 者 简 介 : 胡 向 东 ( , 男 , 浙 江 省衢 州 市 人 , 副 教 授 , 博 士 生 导 师 , 主 要 从 事 隧 道 与地 下 程 等研 究 电 话 ( ; :

1368 上海交通大承学报 够17参 解析解计算还很少涉及.鉴于此,本文采用势函数叠 进而推出 加理论求解4根冻结管以任意形式排列时的稳态温 度场分布,得出了四管以矩形和菱形等形式排列下 地-会 的稳态温度场解析解 并由此得 1基本方程与热势定义 =-Inr+C (5) 当平面上存在和根冻结管时,冻结区内任意 十休中的热传递主要有传导、对流、辐射3种形 式在 般的工程应用中,后两者对推导结果的影响 点的温度势为 相对于前者可以忽略不计,因此,本文的推导中不考 Φ=-(nr,+gln+…+2lnr)+C 虑后2种热传递形式. 根据傅里叶定律 9--k 中=-∑nr+C (6) 式中:9为在单位时间内沿x方向的热流密度:为为 式中:为该点到第i根冻结管中心的距离:g为第 :根冻结管的热流密度:C为积分常数 土体的导热系数:T为土体温度.令巾=kT,将其定 义为热势,则有: 2 无限大区域内单根冻结管的稳态温 9一 度场求解 根据傅里叶定律和热力学第一定律,平面内热 传导的控制方程为 器+-Q+=0 (3) 以将其看作是点源,并使其处于坐标中心,假设冻 管半径为r。,陈土半径为,冻结管表面温度为T 式中:4,q,分别为单位时间内沿x和y方向的热 土体冻结温度为T。,见图1. 流来度:O为在单位时间单位体积内系统从外界吸 收或向外界释放的热量:D为密度:c为比热容 冻土边牙 在推导过程中,将土体假设为各向同性材料,即 沿各个方向的导热系数均相等同时,将问题近似为 稳态温度场来求解,这种方法的误差很小 在订 算区内不考虑系统与外界的热量交换,将热势定义 知稳态条件代人控制方程,则式(3)可简化为 碧+ =0 (4】 式(4)的极坐标形式为 图 )=o 陈结区域内任意一点M的热势函数表达式与 由上述衬论可知,Laplace方程的解即为热势函 式(5)相同.式中,r为任意一点到冻结管的距离,且 数。以单管情形为基,将各管 生热势的原理看作 =√+y,冻土边界一点的温度势为 是各管圆心处存在 冷源,在稳态时该点单位时 内吸收的热量为9,则其会使平面内每点的温度势 -In +C (7) 降低,根据势函数叠加原理,当平面内存在多个这样 冻结管边缘一点的温度势为 的点时,这种热势的降低可以叠加因此,当平面内 布置多根冻结管时,平面内任一点的热势等于各管 In r+C 8) 中心冷源 在该点产生的热势的叠加 联立式(7)与(8)可得: 根据以上假设,在点源周围画半径为r的圆,圆 -=府 周上一点的冻结管热流密度为 将其代人式(5),并利用关系式中=kT、中,=T。和 9:=2x=-2xr9 D,=kT,最终得出无限大区城内单根冻结管稳态温 1994-2016 China Academic Joural Electronic Publishing House All rights reserved.http://www.cnki.net
1 3 6 8 解析 解 计 算 还 很 少 涉 及 鉴 于 此 , 本 文 采 用 势 函 数 叠 加 理 论求 解 根冻 结 管 以 任意 形 式排 列 时 的 稳态 温 度 场 分布 , 得 出 了 四 管 以 矩 形 和 菱 形 等 形 式 排 列 下 的 稳态 温 度场 解 析 解 基本 方 程 与 热 势定 义 土 体中 的热 传递 主 要 有 传 导 、 对 流 、 辐 射 种 形 式 在 一 般 的 工 程应 用 中 , 后两 者 对 推 导 结果 的 影 响 相 对 于前 者可 以 忽 略不 计 , 因 此 , 本文 的 推 导 中 不 考 虑 后 种 热 传递 形式 根 据傅 里 叶 定 律 — — ⑴ 式 中 : 为 在单 位 时 间 内 沿 方 向 的 热 流 密 度 ; 々 为 土 体 的 导 热 系 数 ; : 为 土 体温 度 令 少 々 , 将 其 定 义 为 热 势 , 则 有 : 屯 广一 ⑵ 根 据傅 里 叶 定 律 和 热 力 学 第 一 定 律 , 平 面 内 热 传导 的 控制 方程 为 式 中 : 分 别 为 单 位 时 间 内 沿 和 方 向 的 热 流 密度 ; 为 在 单位 时 间 单 位 体 积 内 系 统 从 外 界 吸 收 或 向 外界 释放 的 热 量 … 为 密 度 ; 为 比 热 容 在 推导 过程 中 , 将土 体 假 设 为 各 向 同 性材 料 , 即 沿 各 个方 向 的 导 热 系 数 均 相 等 同 时 , 将 问 题 近 似 为 稳 态 温度 场 来求 解 , 这 种方 法 的误 差 很 小 在 计 算 区 内 不考 虑 系 统 与 外 界 的 热 量交 换 , 将 热 势 定 义 和 稳 态条 件代 人控 制 方 程 , 则 式 ( 可 简 化 为 式 ( 的 极 坐标 形式 为 去 务。 由 上 述讨论 可知 , 方 程 的 解 即 为 热势 函 数 以 单 管情 形 为 基 础 , 将 各管 产生 热 势 的 原理看 作 是 各管 圆 心处 存 在 一 冷 源 , 在 稳态 时 该点 单 位 时 间 内 吸 收 的 热量 为 《 。 , 则 其 会 使平 面 内 每 点 的 温 度 势 降 低 根 据势 函 数叠 加 原 理 , 当平 面 内 存在 多 个这 样 的 点 时 , 这 种热 势 的 降低 可 以 叠加 因 此 , 当 平 面 内 布 置多 根冻 结管 时 , 平 面 内 任 一 点 的 热 势 等 于 各 管 中 心 冷 源 在 该点 产 生 的 热势 的叠 加 根 据 以 上假 设 , 在点 源 周 围 画 半 径为 的 圆 , 圆 周 上一 点 的 冻结 管热 流 密 度为 — 第 卷 进 而 推 出 少 并 由 此得 当 平 面 上 存 在 ” 根 冻 结 管 时 , 冻 结 区 内 任 意 一 点 的 温 度 势 为 … 即 “ ‘ 丌 式 中 : 为 该 点 到 第 根 冻 结 管 中 心 的 距离 为 第 根 冻 结 管 的 热流密 度 ; 为 积分 常 数 无 限 大 区 域 内 单 根冻 结 管 的 稳态温 度 场 求解 采 用 定 义 热势 函 数 的 方 法来 求 解 无 限 大 区域 内 单 根 冻 结管 的 稳态 温 度 场 由 于 冻 结 管吸 收 热量 , 所 以 将其 看 作 是点 源 , 并 使其 处 于 坐 标 中 心 假 设 冻 结 管 半 径 为 , 冻 土半 径 为 。 冻 结 管 表 面 温度 为 乃 , 土 体冻 结温 度 为 , 见 图 图 无 限 大 区 域 内 单 根 冻 结 管 示 意 图 冻 结 区 域 内 任 意 一 点 的 热 势 函 数 表 达 式 与 式 相 同 式 中 为 任 意 一 点 到 冻 结 管 的 距 离 , 且 冻 土 边 界一 点 的 温 度 势 为 黾 — 冻 结管 边缘 一 点 的 温度 势 为 § 联立式 ( 与 ( 可 得 : 中 — 中。 兀 将 其代 人式 ( , 并 利 用 关 系 式 、 和 办 , 最终 得 出 无 限 大区 域 内 单 根冻 结 管 稳态 温 上 海 交 通 大 学 学 报

第9期 胡向东,等:无限大区域内四管冻结的稳态温度场解析解 1369 度场的解 根据势函数叠加原理,图2中冻结区域内任意 T-+器- 9) 点M的热势为4根冻结管单独作用时所产生的热 热的叠加,其表达式为 式(9)与Trupak提出的单管温度场的解完全相 =-n-2lnn 3无限大区域内4根冻结管任意排列 aIn r-aIn r+C (10) 时的稳态温度场求解 式中,~r分别为M点到冻结管P,一P,的距离 3.14根冻结管以任意形式排列 在实际工程中采用4根冻结管进行冻结时,根 )+y,n=F+(y- 据具体的冻结需求,可将其排列为直线形式,也可将 其排列为矩形或菱形形式为此,本文对无限大区域 n=√x-》+y 内4根冻结管以任意形式排列时的稳态温度场解析 r,=√x-x,)+(y-y) 解进行推导. 冻士边界条件点(0,为十)的温度势为 假设4根冻结管管边缘的热势相同,即4根冻 。=-lhA,一ln- 结管的表面温度均为T,4根冻结管半径均为r。, 体冻结温度为T。,4根冻结管的热流密度分别为 昙nA,-验nA,+C (11) 9990和94根冻结管中心在无限大区内的 式中: 坐标分别为P(,y)、P(x,为)、P(xs,)和 A,=+(+为)F,A=√行+(+y)月 P,(r,,v,)为了俪于推导,将冻结管P,与卫的连 线宗为x轴,冻结管P,至该崔线的垂线定为y轴 A=V+(-- 因此,这3根冻结管中心的坐标变为(1,0)、 由于冻结管半径r。相对于d1、d、d3、d、d: (0,)和(,0).此外,定义陈土边界条件点在 、,和y很小,其对计算结果的影响 轴上,与陈结管P2,中心之间的距离为,该点坐杨 也很小,所以4根冻结管边缘上的边界条件点(,十 为(0,+),4根冻结管之间的距离分别为d、 r。,0)、(0,2一ra)、(x3一r。,0)和(x4,y4十ro)的 d、d,、d,、d,和d,见图2. 温度势可表达为: 条件点 o =-2In ro-sIn di- @片+5) 验lnds-1nd+C (12) 东土边界 pa=-婴lnd-装nn 婴nd-装nd+C (13) pa=-驶lnd,-nd, 验lnn-lnd+c (14) 图?无限大区域内4根冻结管以任意形式排列的示意 Du =-In d -In de Fig.2 nfiniteregio -elnd,-袋lno+C (15) 考虑到x2、y1和y,均为0,因此,图2中有 根据以上假定,4根冻结管边缘的温度势相同 d=√+, d=+ 即=a=a=.在此假设ga=qu d山,=√-x4)+,d,=x-)+ 作919=9a,联立求解式(12)~(15)可得: d5=x3-x1, d。=√xi+(y4-y) 194-016 China Academie Joumal Electronie Publishing House All rights reserved. http://www.cnki.net
第 期 胡 向 东 , 等 : 无 限 大 区 域 内 四 管 冻 结 的 稳 态 温 度 场 解 析 解 度场 的 解 为 式 与 提 出 的 单 管 温 度 场 的 解 完 全 相 同 无 限 大 区 域 内 根 冻 结 管 任 意 排 列 时 的 稳态温 度 场求 解 根 冻 结 管 以 任 意形 式 排列 在实 际 工 程 中 采 用 根 冻结 管 进 行 冻结 时 , 根 据具体 的 冻结 需求 , 可将其排 列 为 直线形 式 , 也 可 将 其 排 列 为 矩形 或 菱形 形式 为 此 , 本文对 无 限 大 区域 内 根冻 结管 以 任 意 形式排 列 时 的稳 态 温度场 解析 解 进 行推 导 假设 根 冻结 管 管 边 缘 的 热 势 相 同 , 即 根 冻 结 管 的 表 面 温度 均为 根 冻 结管半 径均 为 「。 , 土 体 冻 结温 度 为 乃 , 根 冻 结 管 的 热 流 密 度 分 别 为 、 如 和 如 , 根冻 结管 中 心 在无 限 大 区 域 内 的 坐 标 分别 为 , 、 工 , 、 工 , : 和 , 力 ) 为 了 便 于推 导 , 将冻 结管 与 朽 的 连 线 定 为 工 轴 , 冻 结管 至 该 连 线 的 垂 线 定 为 轴 , 因 此 , 这 根 冻 结 管 中 心 的 坐 标 变 为 ( 力 , 、 , 力 ) 和 而 , 此 外 , 定 义 冻 土 边 界 条 件 点 在 轴上 , 与 冻结 管 中 心 之 间 的 距 离 为 该 点 坐 标 为 ( , 力 十 ? ) , 根 冻 结 管 之 间 的 距 离 分 别 为 、 、 、 山 、 £ 和 , 见 图 图 无限 大区 域 内 根 冻结管 以 任 意 形 式 排列 的 示 意 图 考 虑到 和 力 均为 , 因 此 , 图 中 有 : 工 — — 丨 — , 根 据势 函 数 叠加 原理 , 图 中 冻 结 区 域 内 任 意 点 的 热 势 为 根冻 结 管单 独 作用 时 所 产 生 的 热 势 的叠 加 , 其 表达 式为 少 — — 一 式 中 , 分别 为 点 到 冻结 管 的 距离 , 且 厂 — , “工 — 。 — — — 冻 土 边 界条件 点 ( , 力 的 温 度 势 为 少 — — — 式 中 : , — — 由 于冻 结 管 半 径 。 相 对 于 义 、 、 义 、 、 义 、 土 、 々 、 : 、 工 、 和 很 小 , 其 对 计算 结 果 的 影 响 也很小 所 以 根冻结 管边缘 上 的边 界 条件 点 ( , 、 ( , 力 一 厂 、 ( 了 — , 和 ( 工 , 。 ) 的 温度 势 可 表 达为 : 少 — — — 一 — — 一 取 一 — — — — 一 一 一 — 根据 以 上假 定 , 根冻 结管 边缘 的 温 度 势 相 同 , 即 由 在 此 假 设 , 仲 , 仏 沖 , 联立 求 解式 ( ( 可 得 — 平 — —

1370 上瓷交通大学学报 第7 n=D+D+D. 3.34根冻结管以菱形形式排列 F,+F。+F 若4根冻结管以菱形形式排列,则有d=d: 式中: ,-d.在此,将其记为d.d,和d。满足:4d=d店 B=hn2na品-h学nna d,如图3所示. 界面1界面2 品-n4nn,c=lnn G=hn学n缺,G=hn粉 冻土边界 D=hnn经,D,=hnna n-hn禁,R-hnn R,=n(mn先-lnn) R=lh(2n学-lhn) 将式(10)一(15)统一用,和阳表示,并 利用中。和中可得: 图3无限大区域内4根冻结管以菱形排列示意图 Fig.3 Four freeing with rhombu 器一n会十lh号+h光+h光 arrangement 利用 此时:和可简化为n/加式n可简 Φ三是T,中。kT。 化为1.最终所得无限大区域内4根冻结管以菱形 币.=bT=6T.=bT。三6T。三bT 最终得出无限大区域内4根冻结管以任意形式排列 形式排列的稳态温度场的解为 的士体稳态温度场的解为 T=T,+ T=T。十 (仙+420+话n+n恤a)T-/ (n无+nln经+mlh是+pln众)T-T,/ (n是+nng+ln是+lh先) (16) 为验证公式的准确性,采用ANSYS软件进行 3,24根冻结管以等间距直线形式排列 热学数值计算,以模拟假定条件下的温度场分布,并 如果4根冻结管以等间距直线形式排列,则有 与其解析解所得结果进行对比.其中,选取d山:一 d-d:-d=d/3=d/2=d/2,将d1记为d,则 1.0m,d。=0.8m,=1.0m,T=-70℃,Ta= 山一d,均可以用d表示.此外,和可以简化为 0℃,r=54mm的情况进行计算.由式(18)所得温 1n爱/n易作可简化为1.最终得出无限大区域 度场的分布见图4.图5示出了主面 1及主面2(见 图3)上的温度场分布与其数值模拟结果的对比,由 肉安动华风直线底大州电态 图5可以看出,解析解与数值解相吻合,由此验证了 式(18)的正确性. T=T.+ 3.44根冻结管以矩形形式排列 当4根冻结管以矩形形式排列时,为了便于解 析解公式的推导,将4根冻结管分别置于4个象阳 (n2d+nln8d) (17) 电其中.d,=d、.d。=d..d。=d。日=d+d 式(17)与文献[4-5]中所得4根冻结管以等间距直 此排列形式下的稳态温度场解析解求解方法以及求 线形式排列时的稳态温度场解析解一致,后者是假 解过程中的假设与前述问题相同.由此可得 设土体冻结温度为0℃时的特定解。 ==1.最终所得无限大区域内4根冻结管以矩 1994-016China Academic Joumal Eleetronic Publishing House All rights reserved.http://www.cnki.ne
1 3 7 0 = D i + P 2 ~ h D 3 7 3 — 式 中 : 參 争字 , 争 么 铃 仝 令么 令 么 。 — — — — — 々 厂 么 孛 幹 么 合 铃 垒 丰 孛 一 孛 将式 ( ( 统 一 用 作 、 、 和 。 表 不 , 并 利 用 和 办 可 得 : — 屯 广 色 利 用 最 终 得 出 无 限 大 区 域 内 根 冻 结管 以 任 意 形 式排 列 的 土 体稳 态 温度 场的 解 为 免 十 … 专 十, 老 — 完 — 。 根 冻 结 管 以 等 间 距 直线 形 式排 列 如 果 根 冻 结 管 以 等 间 距 直线 形式 排 列 , 则 有 将 记 为 , 则 均 可 以 用 表 示 此 外 , 和 可 以 简 化 为 可 简 化 为 最 终 得 出 无 限 大 区 域 内 根 冻结 管 以 等 间 距直 线 形 式排 列 的 稳态 温度 场 的 解 为 ¥ 「 。 式 ( 与 文 献 中 所 得 根冻 结 管 以 等 间 距 直 线 形 式排 列 时 的 稳 态 温 度 场解 析 解 一 致 , 后 者 是假 设 土 体冻结 温度 为 ° 时 的 特定 解 第 卷 根 冻 结 管 以 菱 形 形 式 排 列 若 根 冻 结 管 以 菱 形 形 式 排列 , 则 有 义 在此 , 将 其记 为 丄 和 土 满 足 : 忒 忒 , 如 图 所示 界面 界 面 图 无 限 大 区 域 内 根 冻 结 管 以 菱 形 排 列 示 意 图 此时 , 和 识 可 简 化 为 可 简 化为 最 终 所得 无 限 大 区 域 内 根 冻 结 管 以 菱 形 形 式排列 的稳 态 温度 场 的 解 为 ¥ 「 。 £ 为验 证公 式 的 准 确 性 , 采 用 软 件 进 行 热 学数值 计算 , 以 模拟 假 定条件 下 的 温度 场 分 布 , 并 与 其 解 析 解 所 得 结 果 进 行 对 比 其 中 , 选 取 , , — — ° ° 的 情况 进行 计算 由 式 ( 所得 温 度 场 的分 布 见 图 图 示 出 了 主 面 及 主 面 见 图 上的 温 度场分 布与 其数 值 模 拟结 果 的 对 比 由 图 可 以 看 出 , 解 析解 与 数 值解 相 吻 合 , 由 此验证 了 式 ( 的 正 确 性 根冻 结 管 以 矩 形 形式 排列 当 根 冻 结 管 以 矩 形 形 式 排列 时 , 为 了 便 于 解 析解 公式 的 推导 , 将 根 冻 结 管 分 别 置 于 个 象 限 中 其 中 , … , 土 , 且 名 名 此排 列 形 式 下 的 稳态 温度 场 解析 解求 解 方法 以 及求 解 过程 中 的 假 设 与 前 述 问 题 相 同 由 此 可 得 卞 最终所 得无 限 大 区 域 内 根 冻结 管 以 矩 上 海 交 通 大 学 学 报
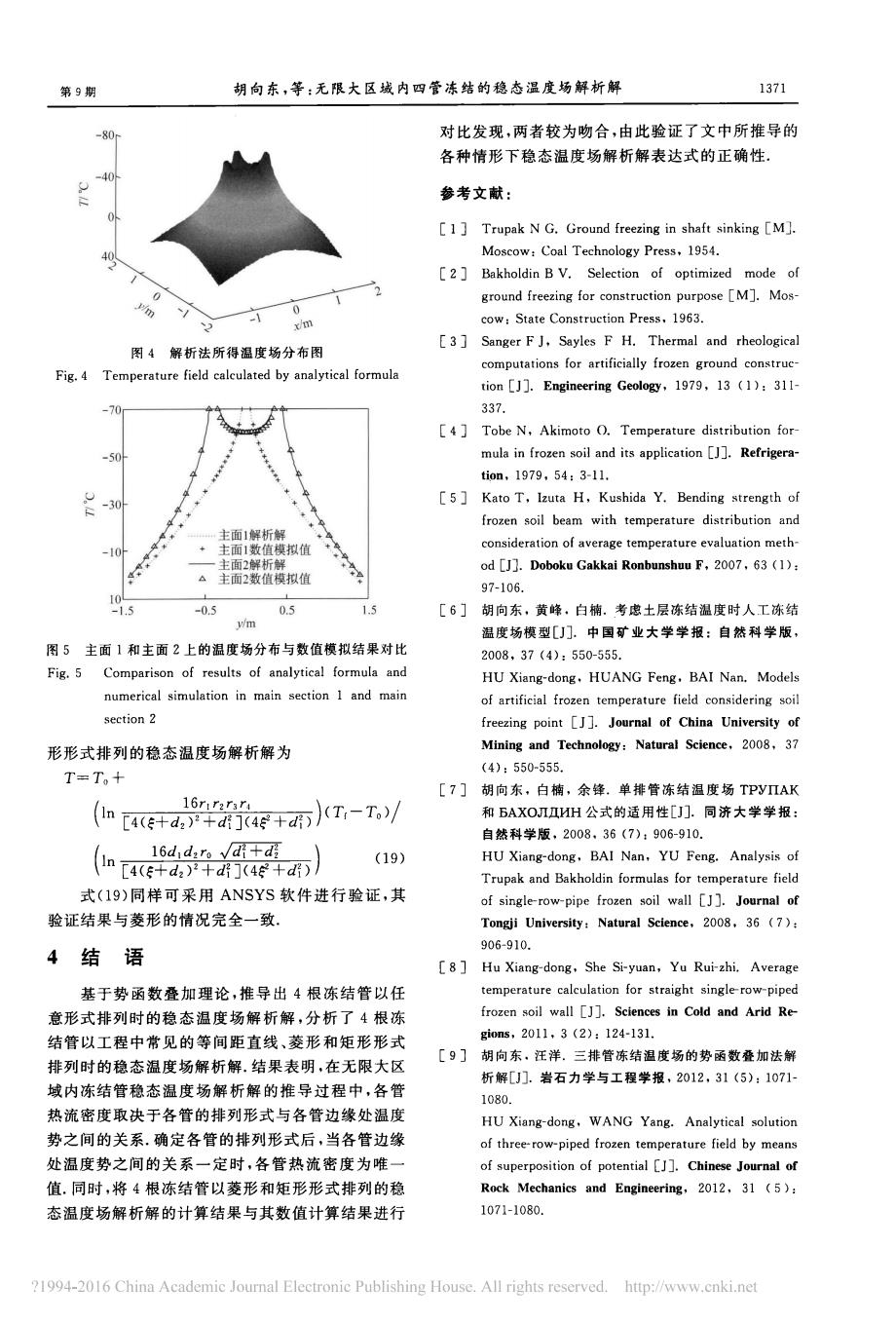
第9期 胡向东,等:无限大区城内四管冻结的稳态温度场解析解 1371 -80 对比发现,两者较为吻合,由此验证了文中所推导的 各种情形下稳态温度场解析解表达式的正确性 参考文献: 1]Trupak N G.Ground freezing in shaft sinking [M] M :Coal Technology Press.1954. round freezing for con 10 pose [M].Mos- 闲4解析法所得温度场分布图 [3] Sanger FJ.Sayles F H.Thermal tificially tu tion.Enginee 1979.13:31 237 re distribution for mula in fro its i0m.1979.54,3-11 、-30 [s] Kato T.Izuta H.Kushida Y.Bending ngth of with te tu o 主面解折拟值 od Doboke Gakkai Ronbunshur .2007.6313 05 [6] 中国矿业大学学报:自然科学假】 图5主面】和主面2上的温度场分布与数值模拟结果对比 :550-555. Fig.5 Comparison of results of analytical formula and HU Xia ofanicalo HUANG Fenz, BAI Nan.Models numerical simulation in main section 1 and main section 2 int[J] Uni 形形式排列的稳态温度场解析解为 and Tec 2008.37 T=T,+ [7] 胡向东 滴,余峰。单排管冻结溢度场TP (ae+d+水T-/ 公式的 同济 大学 学报 白然科学板 16d d:ro vdi+di (19) and Bakholdin fo 式(19)同样可采用ANSYS软件进行验证,其 验证结果与菱形的情况完全一致. University 08.36(7) 4结语 [8] Hu Xiang-dong.She Si-y Yu Rui-zhi.Ave a age 基于势函数叠加理论,推导出4根冻结管以任 o 意形式排列时的稳态温度场解析解,分析了4根冻 soil wall [11.Se and Arid Re 9019/21.124.121 结管以工程中常见的等间距直线、菱形和矩形形式 排列时的稳态温度场解析解.结果表明,在无限大区 [9] 胡向东,洋,三排管冻纺温度场的势函数叠加法解 析解].岩石力学与工程学报,2012,31(5):1071 域内冻结管稳态温度场解析解的推导过程 各管 1080 热流密度取决于各管的排列形式与各管边缘处温度 HU Xiang-dong.WANG Yang.Analytical solution 势之间的关系.确定各管的排列形式后,当各管边缘 of thre w-piped frozen ter rature field hy mean 处温度势之间的关系一定时,各管热流密度为唯 of superposition of potential J Chinese Jourmal of 值,同时,将4根冻结管以菱形和矩形形式排列的稳 Rock Mechanics and Engineering.2012.31(5): 态温度场解析解的计算结果与其数值计算结果进行 1071-1080. 1994-2016 China Academic lournal electronic Publishing House.All rights reserved.htp://www.cnki.net
第 期 胡 向 东 , 等 : 无 限 大 区 域 内 四 管 冻 结 的 稳 态 温 度 场 解析 解 图 解 析 法 所 得 温 度 场 分布 图 图 主 面 和 主 面 上 的 温 度场 分 布 与 数 值 模拟 结 果 对 比 形 形 式排 列 的 稳 态 温 度 场 解 析 解 为 式 ( 同 样 可 采 用 软 件 进 行 验 证 , 其 验证 结果 与 菱 形 的 情 况 完 全一 致 结 语 基 于 势 函 数 叠 加 理 论 , 推 导 出 根 冻 结 管 以 任 意 形 式排 列 时 的 稳 态 温 度 场解 析 解 , 分 析 了 根 冻 结管 以 工 程 中 常 见 的 等 间 距 直 线 、 菱 形 和 矩 形 形 式 排 列 时 的 稳态 温度 场解 析 解 结 果 表 明 , 在 无 限 大 区 域 内 冻 结 管稳 态 温 度 场 解 析 解 的 推 导 过 程 中 , 各 管 热 流 密 度 取决 于 各 管 的 排 列 形 式 与 各管 边 缘 处 温 度 势 之 间 的 关 系 确 定 各管 的 排 列 形 式 后 , 当 各 管 边缘 处 温度 势之 间 的 关 系 一 定 时 , 各 管 热 流 密 度 为 唯 一 值 同 时 , 将 根 冻结 管 以 菱 形 和 矩 形 形式 排列 的 稳 对 比发 现 , 两 者 较 为 吻 合 , 由 此验 证 了 文 中 所 推 导 的 各 种 情 形 下 稳态 温度 场 解 析 解 表 达式 的 正 确 性 参 考 文 献 : : , : , , , , 」 , , , , , , : 胡 向 东 , 黄 峰 , 白 楠 考 虑 土 层 冻 结温 度 时 人 冻 结 温 度 场 模 型 中 国 矿 业 大 学 学 报 : 自 然 科 学 版 , : : , : 胡 向 东 , 白 楠 余 锋 单 排 管 冻 结 温 度 场 和 公 式 的 适 用 性 同 济 大 学 学 报 : 自 然 科学 版 , : : , : 胡 向 东 , 汪 洋 三 排 管 冻 结 温 度 场 的 势 函 数 叠 加 法 解 析 解 岩 石 力 学 与 工 程 学报 , : , , 主 面 解 析解 主 面 数 值 模拟 值 主面 解析 解 主面 数值模拟值 态 温 度 场 解 析 解 的 计算 结果 与 其 数值 计算 结果 进 行