
第品春装用 文章编号.0253-374X(2015)03-038G-06 D)I:10.11908/i.issn.0253-374x.2015.03.010 双排管冻结稳态温度场广义解析解 胡向东12,韩延广12,虞兴福 (L.同济大学岩士及地下工程教育部重点实验室,上海200092: 2.同济大学士木工程学院.上寿200092:3.新江大学城市学院工程学院,新江杭州310015) 痛要。人工地结法工中,对于理排的布管形,巴密尔 solution to the steady-state emperature field was derived for 金给出了双排管冻结稳态温度场解析解。但巴霍尔金解析解 ing in 只针对对齐和标准销位这两种情况,不能完全满足现实的型 pip of the 求,针对工程中的不规则布管问题,利用调和方程边界条件 可分离性,通过叠加单排冻结巴摆尔金问恩解和线性温度场 问题解,获得了特殊单摆冻结问题的解析解:借鉴特殊单排 温度场问题,完成布管形式复杂的双排管冻结温度场问题的 solution meets the accucy requirement in 广义解析解,并利用ANSYS数值模拟和物理模型实验结果 engineering 验证了解析解的正确性 Keywords artificial ground field 关键词:人工地层冻结:温度场:单排管:双排管解析解 single-row-pipe freezing double-row-pipe freezing analytical olution:harmonie equations 调和方程 中图分类号:TK124 文献标志码:A 人工地层冻结技术,由于其冻土推幕的良好封 Generalized Analytical Solution to Steady-state 水效果和力学强度,因此广泛应用于地下工程施1 Temperature Field of Double-row-pipe Freezing 中,在施工过程中,掌握冻土帷幕的厚度和力学性厨 HU Xiangdong HAN Yangwang.YU Xingfu 等参数是非常重要的,而这些参数均依赖于冻结温 (1.Key Laboratory of Geotechnical and Underground Engineering of 度场的分布因此,温度场理论是冻结法理论的基 the Ministry of Education.Tongii University.Shanghai 200092. China:2.College of Civil Engineering.Tongii University.Shanghai 温度场理论研究分为瞬态温度场和稳态温度 200092.China:3.School of Engineering.Zhejiang University City 场,由于数学上的困难,多管冻结的瞬态温度场解析 College.Hanezhou 310015.China) 解难以获得,不能满足工程中多管、排管和圈管等复 Abstract.for the doublerow atrangement of freezing pipes 杂的布管形式的要求:而稳态温度场相对简单日能 in artificial ground frrezing.Bakholdin gave an analytical 够满足工程上的精度要求,因此是各国学者研究的 olution to the stead-state temrerature field However.the 重点内容.目前,世界上最流行和实用的人工冻结移 solution only aimed at the inline and general staggered 态温度场解析解有单管冻结温度场公式[),两管至 ents.which could not mee 五管直线排列冻结温度场公式,单排管冻结温度 gements of freezing pipes in 场公式以及双排管冻结温度场公式等.笔者对这 e.in this field of double 些公式进行了完善与应用性研究[],并完成了绝热 of boundary 幼界附诉单管和双管[10任章排列的三管[1】和四 管,冻结管温度不等时的双管、单排管,冻 a special single-row-pip solved b 结管温度相等时的三排管[】、冻土帷幕厚度非对称 problen was superposition of the singl ow-pipe solution and the linea 发的单推管和内部冻实的单围管结温度场解 emperature field solution.Then.the generalized analytical 析解切的推导 作 朝东(1961一),男, 1994-2015 China Acade lournal electronic publishing House http:/ www.cnki.ne
第43卷第3期 2015年3月 同 济 大 学 学 报(自 然 科 学 版) JOURNALOFTONGJIUNIVERSITY(NATURALSCIENCE) Vol.43No.3 Mar.2015 文章编号:0253-374X(2015)03-0386-06 DOI:10.11908/j.issn.0253-374x.2015.03.010 收稿日期:2013-12-05 基金项目:国家自然科学基金(51178336);浙江省自然科学基金(LZ13E080002) 第一作者:胡向东(1961—),男,副教授,博士生导师,工学博士,主要研究方向为隧道与地下工程.E-mail:anton.geotech@tongji.edu.cn 双排管冻结稳态温度场广义解析解 胡向东1,2,韩延广1,2,虞兴福3 (1.同济大学 岩土及地下工程教育部重点实验室,上海 200092; 2.同济大学 土木工程学院,上海 200092;3.浙江大学城市学院 工程学院,浙江 杭州 310015) 摘要:人工地层冻结法施工中,对于双排的布管形式,巴霍尔 金给出了双排管冻结稳态温度场解析解.但巴霍尔金解析解 只针对对齐和标准错位这两种情况,不能完全满足现实的要 求.针对工程中的不规则布管问题,利用调和方程边界条件 可分离性,通过叠加单排冻结巴霍尔金问题解和线性温度场 问题解,获得了特殊单排冻结问题的解析解;借 鉴 特 殊 单 排 温度场问题,完成布管形式复杂的双排管冻结温度场问题的 广义解析解,并利用 ANSYS数值模拟和物理模型实验结果 验证了解析解的正确性. 关键词:人工地层冻结;温度场;单排管;双排管;解析解; 调和方程 中图分类号:TK124 文献标志码:A GeneralizedAnalyticalSolutiontoSteady-state TemperatureFieldofDouble-row-pipeFreezing HU Xiangdong1,2,HAN Yanguang1,2,YU Xingfu3 (1.KeyLaboratoryofGeotechnicalandUndergroundEngineeringof the Ministry of Education,Tongji University,Shanghai200092, China;2.CollegeofCivilEngineering,TongjiUniversity,Shanghai 200092,China;3.SchoolofEngineering,ZhejiangUniversityCity College,Hangzhou310015,China) Abstract:Forthedouble-rowarrangementoffreezingpipes inartificialgroundfreezing,Bakholdin gavean analytical solutiontothesteady-statetemperaturefield.However,the solution only aimed at the inline and general staggered arrangements,whichcouldnotmeetpracticalrequirements. Forirregulararrangementsoffreezingpipesinengineering practice,inthispaper,ageneralizedanalyticalsolutiontothe steady-statetemperaturefieldofdouble-row-pipefreezingwas proposed. First, based on the separability of boundary conditionsforharmonicequations,aspecialsingle-row-pipe freezing problem was solved by superposition of the Bakholdin’s single-row-pipe solution and the linear temperaturefieldsolution.Then,thegeneralizedanalytical solutiontothesteady-statetemperaturefield wasderivedfor double-row-pipefreezinginirregulararrangementsaccording tothespecialsingle-row-pipesolution.Comparison ofthe analyticalsolution withthenumericalthermalanalysisshows thatthe analytical solution is precise enough,and the experimentalresults of physical modelindicates thatthe analytical solution meets the accuracy requirement in engineering. Key words:artificialgroundfreezing;temperaturefield; single-row-pipefreezing;double-row-pipefreezing;analytical solution;harmonicequations 人工地层冻结技术,由于其冻土帷幕的良好封 水效果和力学强度,因此广泛应用于地下工程施工 中.在施工过程中,掌握冻土帷幕的厚度和力学性质 等参数是非常重要的,而这些参数均依赖于冻结温 度场 的 分 布.因 此,温 度 场 理 论 是 冻 结 法 理 论 的 基 础. 温度场理论研究分为瞬态温度场和稳态温度 场,由于数学上的困难,多管冻结的瞬态温度场解析 解难以获得,不能满足工程中多管、排管和圈管等复 杂的布管形式的要求;而稳态温度场相对简单且能 够满足工程上的精度要求,因此是各国学者研究的 重点内容.目前,世界上最流行和实用的人工冻结稳 态温度场解析解有单管冻结温度场公式[1],两 管 至 五管直线排列冻结温度场公式[2],单 排 管冻 结 温 度 场公式以及双排管冻结温度场公式[3-4]等.笔者对这 些公式进行了完善与应用性研究[5-9],并完成了绝热 边界附近 单 管 和 双 管[10]、任意排列的三管[11]和 四 管[12]、冻结管温度不等时的双管[13]、单 排 管[14]、冻 结管温度相等时的三排管[15]、冻土帷幕厚度非对称 发展的单排管[16]和内部冻实的单圈管冻结温度场解 析解[17]的推导.

第3期 胡向东,等:双持管冻结稳态温度场广义解析解 387 单排和双排直线布置是冻结法中最常见的冻结 称发展,其将退化为经典单排管冻结巴霍尔金解) 管布置方式.对此,巴霍尔金给出了单排和双排管冻 结稳态温度场解析解),其中双排管解折解解决了 2双排管冻结温度场广义解析解 等管距的两排管对齐和错位 分之 管间距(以下 简称标准错位)这两种布管方式的问题.但双排管冻 本文考虑的冻结管布管形式为第 一排冻结管间 结时,对齐方式不止对齐和标准错位这两种情况,两 距与第二排冻结管间距不一致并且第二排冻结管相 排管错位量可能是任意的:另外,两排管的管间距有 对于第一排冻结管有偏移量和:在冻土推幕充分交 可能不一致.而这些布管形式特殊的问题尚无解析 圈后,即冻结后期,冻土帷幕边界近似为直线边界, 解.本文通过引入特殊的单 冻结温度场问恩,并 则双排管冻结广义问题 图2所示.其中,L为冻结 结合调和方程边界可分离性,完成了适应特殊布 管排间距.这里需要说明,第一排冻结管间距:和第 管方式的双排管冻结温度场的广义解析解。 一挂族结管间距。是相互独立的,即1,可以大于 ,,也可以小于,,并不相互制约.另外,冻土推幕厚 1特殊的单排管冻结温度场 度和品也是相互独立的.图2表示的冻结问愿应 理解为双排管冻结的普遍问题,而不是仅指图中所 为了求解广义双推管冻结问题,引入特殊的单 示的一种模型 排管冻结温度场,其冻土雌幕非均匀对称发展.这种 第二冻土边界1y 温度场问题如图1所示 第1管 第一 第二冻士边界 6 第一冻士边界 第一冻土边界 图1特殊的单排管冻结温度场模型 其温度场数学模型为 Fig.1 Model of special single-row-pipe freezing 此温度场的数学模型为 T(x,一(台十L/2)=T。,第一冻土边界 臣+票-0 T(x,点+L/2)-T。,第二冻土边界 (3) T(,一L/2+n)=T,第一排冻结管 T(.一名)=T。。第一族土边界 (1 T(+l,,L/2+r。)=T,第二排冻结管 T(,)=T。,第二冻士边界 根据边界条件可分离性),将上述问遐分解为 T(,r)■T,冻结管处 第一排和第二排冻结管温度场问题.即 式中:1为冻结管管间距:白和点均为冻土帷幕厚 度:。为族结管半径:T。为冻土雄幕边界温度:T。为 +=0 东结管表面温度丁表示温度场的分布。笔者已在文 T(r.- (十L/2)=T。,第一冻土边界 献[16]中给出了上述问题的解 (4) T(x,6+L/2)一T。,第二冻土边界 T= T,(j1,-L/2+r)=T-Tn,第一排管 T(A-吾+8音十元 (2) T(e十:,L/2+)=T,第二排管 A=h[2(osh學-cos竿)】 +-0 T:(x,-(+L/2)=0,第一冻土边界 T-T。 (5) T:(x,+L/2)=0,第二冻土边界 T(l1,一L/2+)=Ta,第一排管 对于式(2),当白=合=时,即两侧冻土惟幕对 T:(w+j,L/2+)=T-T,第二排管 1994-2015 China Academic Joumal Electronic Publishing House.All rightsr http://www.cnki.ne
第3期 胡向东,等:双排管冻结稳态温度场广义解析解 单排和双排直线布置是冻结法中最常见的冻结 管布置方式.对此,巴霍尔金给出了单排和双排管冻 结稳态温度 场 解 析 解[3],其中双排管解析解解决了 等管距的两排 管 对 齐 和 错 位 二 分 之 一 管 间 距(以 下 简称标准错位)这两种布管方式的问题.但双排管冻 结时,对齐方式不止对齐和标准错位这两种情况,两 排管错位量可能是任意的;另外,两排管的管间距有 可能不一致.而这些布管形式特殊的问题尚无解析 解.本文通过引入特殊的单排管冻结温度场问题,并 结合调和方程边界可分离性[18],完成了适应特殊布 管方式的双排管冻结温度场的广义解析解. 1 特殊的单排管冻结温度场 为了求解广 义 双 排 管 冻 结 问 题,引 入 特 殊 的 单 排管冻结温度场,其冻土帷幕非均匀对称发展.这种 温度场问题如图1所示. 图1 特殊的单排管冻结温度场模型 Fig.1 Modelofspecialsingle-row-pipefreezing 此温度场的数学模型为 2 T x2 +2 T y2 =0 T(jl,-ξ1)=T0,第一冻土边界 T(jl,ξ2)=T0,第二冻土边界 T(jl,r0)=Tf, 烅 烄 烆 冻结管处 (1) 式中:l为 冻 结管 管 间 距;ξ1 和ξ2 均为冻土帷幕厚 度;r0 为冻结管半径;T0 为冻土帷幕边界温度;Tf 为 冻结管表面温度;T 表示温度场的分布.笔者已在文 献[16]中给出了上述问题的解. T = TA A- π l 2ξ1ξ2 ξ1 +ξ2 + π l ξ1 -ξ2 ( ξ2 +ξ1 y)+T0 (2) A=1 2ln 2 cosh2πy l -cos2πx [ ( l )] TA = Tf-T0 ln2πr0 l -2π l ξ1ξ2 ξ1+ξ2 对于式(2),当ξ1=ξ2=ξ时,即两侧冻土帷幕对 称发展,其将退化为经典单排管冻结巴霍尔金解[3] . 2 双排管冻结温度场广义解析解 本文考虑的冻结管布管形式为第一排冻结管间 距与第二排冻结管间距不一致并且第二排冻结管相 对于第一排冻 结 管 有 偏 移 量 w;在 冻 土帷 幕 充 分 交 圈后,即冻结 后 期,冻土帷幕边界近似为直线边界, 则双排管冻结广义问题如图2所示.其中,L 为冻结 管排间距.这里需要说明,第一排冻结管间距l1 和第 二排冻 结 管 间 距l2 是 相 互独 立 的,即l1 可 以 大于 l2,也可以小于l2,并不相互制约.另外,冻土帷幕厚 度ξ1 和ξ2 也是相互独立的.图 2表示的冻结问题应 理解为双排管冻结的普遍问题,而不是仅指图中所 示的一种模型. 图2 广义双排管冻结温度场模型 Fig.2 Modelofgeneralizeddouble-row-pipefreezing 其温度场数学模型为 2 T x2 +2 T y2 =0 T(x,- (ξ1 +L/2))=T0,第一冻土边界 T(x,ξ2 +L/2)=T0,第二冻土边界 T(jl1,-L/2+r0)=Tf,第一排冻结管 T(w+jl2,L/2+r0)=Tf, 烅 烄 烆 第二排冻结管 (3) 根据边界条件可分离性[18],将上述问题分解为 第一排和第二排冻结管温度场问题.即 2 T1 x2 +2 T1 y2 =0 T1(x,- (ξ1 +L/2))=T0,第一冻土边界 T1(x,ξ2 +L/2)=T0,第二冻土边界 T1(jl1,-L/2+r0)=Tf-Tf1,第一排管 T1(w+jl2,L/2+r0)=Tf2, 烅 烄 烆 第二排管 (4) 2 T2 x2 +2 T2 y2 =0 T2(x,- (ξ1 +L/2))=0,第一冻土边界 T2(x,ξ2 +L/2)=0,第二冻土边界 T2(jl1,-L/2+r0)=Tf1,第一排管 T2(w+jl2,L/2+r0)=Tf-Tf2, 烅 烄 烆 第二排管 (5) 378

38 问济大学学报(白然科学版) 第43卷 其中,Tn和T为参数.设想式(4)表示的温度场问 腰是一种特殊的单挂管冻结间题,则先老虑满足第 -+兴-T 和第二冻土边界条件及第一排冻结管条件的温度 场通解为 M- 五=+[A- 266 +】 (6) N- T-Ta- 经整理后得双排管冻结广义解析解 T-Ti+T:- A-支nf2(eo2巡/2-os2')】 (T:-T)生点奇士(A 2 由于T:为常数,则问题(4)的解必须满足在 =L/2十。的值为常数T,而与x值无关,这是个 经学+云干+》十 先决条件 对于式(6),由于只有A:这部分与x有关,将 (红-工)款立,(A- (e十l,L/2十m)带入A,可以得到 A-2-a红四】 ++-)+T (10 在一般的工程实际中冻结管间距与排间距/L 为0.51.0,则 A=h[2ohav/2-o】 A= h2(osh2y/2-os2a-四1 所以在y=L/2+%,A的值与x值无关,则式 (6)的值在y=L/2+n也与r值无关, 因此式(6)满 当考虑=点=:1=1=【时,则式(10)简化 足问题(4)的第二排冻结管处条件的先决要求,因此 为 将第二排冻结管处条件带入式(6)得到 T= 26 n-20-2++ (7) (11 同理,对于式(5)表示的温度场问恩,先考虑满 足第一和第二冻土边界条件及第二挂冻结管处条件 的温度场通解 T.TALA:- 「oh2y1/2-co2= 对于式(11),当=0时,即为双排管对齐排列 ++特-] (8) 的巴霍尔金解;当■1/2时,即为双排管标准错位 -T 排列的巴霍尔金解[可 T 3解析解准确性检验 3.1与稳态温度场数值模拟的对比 同理T,需要满足 上述推导过程中采用了一定的简化处理,故有 Tn-Te无a++8 268 (9)必要对解的准确性进行验证,因此采用ANSYS进 联立求解式(7)和(9)得 行稳态数值模拟参数选择采用工程上常用的数值 -- 工程上排间距L的取值范围为1.0~ :6,而冻 管间距l/L通常为0.5一1.0,另外冻土椎幕厚度/0 1994-2015 China Academic Joumal Electronic Publishing House.All rights reserved.http://www.enkine
同 济 大 学 学 报(自 然 科 学 版) 第43卷 其中,Tf1和Tf2为 参 数.设想 式(4)表示的温度场问 题是一种特殊的单排管冻结问题,则先考虑满足第 一和第二冻土边界条件及第一排冻结管条件的温度 场通解为 T1 =T0 +TA1[A1 -2π l1 ξ1(ξ2 +L) ξ1 +ξ2 +L+ π l1 ξ1 -ξ2 -L ξ2 +L+ξ1 y+L ( )2 ] (6) TA1= Tf-Tf1-T0 ln2πr0 l1 -π l1 2ξ1(ξ2+L) ξ1+ξ2+L A1=1 2ln 2 cosh2π(y+L/2) l1 -cos2πx [ ( l1 )] 由于Tf2为常 数,则问 题(4)的解必须满足在y =L/2+r0 的 值 为常 数 Tf2,而 与x 值 无 关,这是 个 先决条件. 对于式(6),由 于 只 有 A1 这 部 分与x 有 关,将 (w+jl2,L/2+r0)带入A1,可以得到 A1 = 1 2ln 2 cosh2π(L+r0) l1 -cos2π(w+jl2) [ ( l1 )] 在一般的工程实际中冻结管间距与排间距l1/L 为0.5~1.0,则 cosh2π(L+r0) l1 cos2π(w+jl2) l1 所以在y=L/2+r0,A1 的值与x 值无关,则式 (6)的值在y=L/2+r0 也与x值无关,因此式(6)满 足问题(4)的第二排冻结管处条件的先决要求,因此 将第二排冻结管处条件带入式(6)得到 Tf2 =-TA1 π l1 2ξ1ξ2 ξ2 +L+ξ1 (7) 同理,对于式(5)表示的温度场问题,先 考 虑 满 足第一和第二冻土边界条件及第二排冻结管处条件 的温度场通解 T2 =TA2[A2 -2π l2 ξ2(ξ1 +L) ξ1 +ξ2 +L+ π l2 ξ1 -ξ2 +L ξ2 +L+ξ1 y-L ( )2 ] (8) TA2= Tf-Tf2 ln2πr0 l2 -π l2 2ξ2(ξ1+L) ξ1+ξ2+L A2=1 2ln 2 cosh2π(y-L/2) l2 -cos2π(x-w) [ ( l2 )] 同理Tf1需要满足 Tf1 =-TA2 π l2 2ξ1ξ2 ξ2 +L+ξ1 (9) 联立求解式(7)和(9)得 Tf1 = MN +N MN -1(Tf-T0) Tf2 = MN +M MN -1(Tf-T0) M = π l1 2ξ1ξ2 ξ1 +L+ξ2 ln2πr0 l1 - π l1 2ξ1(ξ2 +L) ξ1 +L+ξ2 N = π l2 2ξ1ξ2 ξ1 +L+ξ2 ln2πr0 l2 - π l2 2ξ2(ξ1 +L) ξ1 +L+ξ2 经整理后得双排管冻结广义解析解 T =T1 +T2 = (Tf-T0)MN +M 1-MN l1 π ξ2 +L+ξ1 2ξ1ξ2 ·(A1 - 2π l1 ξ1(ξ2 +L) ξ1 +ξ2 +L+ π l1 ξ1 -ξ2 -L ξ2 +L+ξ1 y+L ( )2 )+ (Tf-T0)MN +N 1-MN l2 π ξ2 +L+ξ1 2ξ1ξ2 ·(A2 - 2π l2 ξ2(ξ1 +L) ξ1 +ξ2 +L+π l2 ξ1 -ξ2 +L ξ2 +L+ξ1 y-L ( )2 )+T0 (10) A1 = 1 2ln 2 cosh2π(y+L/2) l1 -cos2πx [ ( l1 )] A2 = 1 2ln 2 cosh2π(y-L/2) l2 -cos2π(x-w) [ ( l2 )] 当考虑ξ1=ξ2=ξ;l1=l2=l时,则 式(10)简 化 为 T = Tf-T0 ln2πr0 l -2πξ l m2(x,y)- π l ( (2ξ+L) )+T0 (11) m2(x,y)= 1 2ln 4{ cosh2π(y+L/2) l -cos2πx [ l ]· cosh2π(y-L/2) l -cos2π(x-w) [ l ]} 对于式(11),当 w=0时,即为双排管对齐排列 的巴霍尔金解;当 w=l/2时,即为双排管标准错位 排列的巴霍尔金解[3] . 3 解析解准确性检验 3.1 与稳态温度场数值模拟的对比 上述推导过程中采用了一定的简化处理,故 有 必要对解的准确性进行验证,因 此 采 用 ANSYS进 行稳态数值模拟.参数选择采用工程上常用的数值. 工程上排间距L 的取值范围为1.0~1.6m,而冻结 管间距l/L 通常为0.5~1.0,另外冻土帷幕厚度ξ/l 388
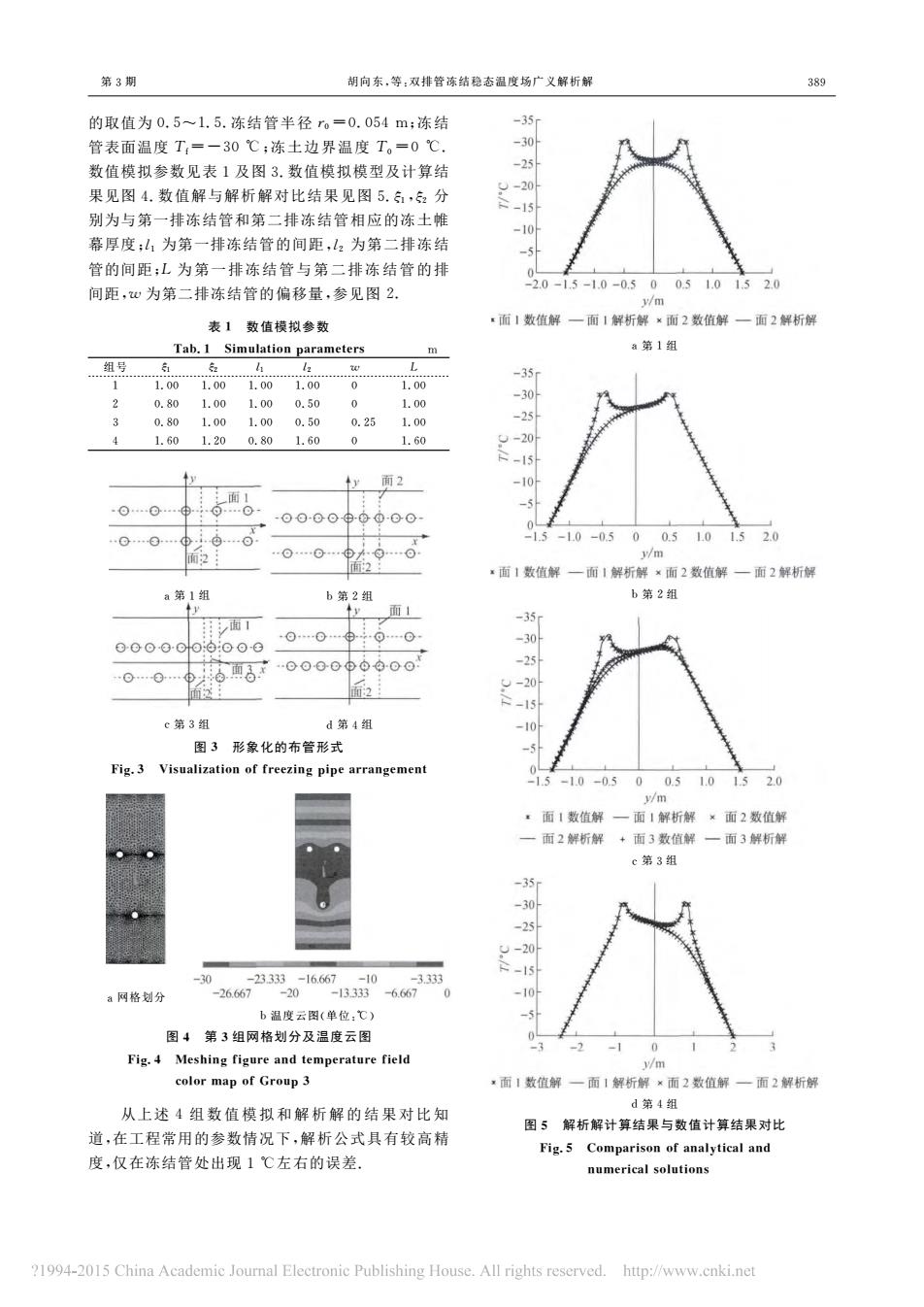
第3期 胡向东,等:双持管冻结稳态温度场广义解析解 的取值为0.51.5.冻结管半径r。=0.054m:冻结 管表面温度T=一30℃:冻土边界温度T。=0℃ 数值模拟参数见表1及图3数值模拟模型及计算结 果见图4.数值解与解析解对比结果见图5,分 别为与第一排冻结管和第 二排冻结管相应的冻土韩 幕厚度:山1为第一排冻结管的间距,1。为第二排陈结 管的间距:L为第一排冻结管与第二排冻结管的排 间距,心为第二排冻结管的偏移量,参见图2. 5-1.0-05 表1数值模拟参数 ·面1数值解一面1解析解×面2数值解一面2解析 Tab.1 Simulatio a第1姐 组号 30 0.80 1.0 1.000.50 0.251.00 1.60 2 -10 00-000000 915-10-05005101520 面2数值解一面2解析 b第2组 第 面1 0…00… c第3组 d第4组 图3形象化的布管形式 Fig.3 Visualization of freezing pipe arrangement 915-10-0500510520 ·面1数 / 解析解面2数值 面2解析解 一面3解析 66 a网格划分 0 图单位. 图4第3组网格划分及温度云 Fig.4 mperature ficld /n 面1数值解 一面1解析 面2数值解一面2解析 第4 从上述4组数值模拟和解析解的结果对比知 道,在工程常用的参数情况下,解析公式具有较高精 图5解析解计算结果与数值计算结果对比 Fig.S on of analytical and 度,仅在冻结管处出现1℃左右的误差。 1994-2015 China Academic Joumal Electronic Publishing House.All rights http://www.cnki.ne
第3期 胡向东,等:双排管冻结稳态温度场广义解析解 的取值为0.5~1.5.冻结管半径r0=0.054m;冻结 管表面温度Tf=-30 ℃;冻土边界温度 T0=0 ℃. 数值模拟参数见表1及图3.数值模拟模型及计算结 果见图4.数值解与解析解对比结果见图5.ξ1,ξ2 分 别为与第一排冻结管和第二排冻结管相应的冻土帷 幕厚度;l1 为第一排冻结管的间距,l2 为第二排冻结 管的间距;L 为 第 一排 冻 结 管 与 第 二 排 冻 结 管 的 排 间距,w 为第二排冻结管的偏移量,参见图 2. 表1 数值模拟参数 Tab.1 Simulationparameters m 组号 ξ1 ξ2 l1 l2 w L 1 1.00 1.00 1.00 1.00 0 1.00 2 0.80 1.00 1.00 0.50 0 1.00 3 0.80 1.00 1.00 0.50 0.25 1.00 4 1.60 1.20 0.80 1.60 0 1.60 a第1组 b第2组 c第3组 d第4组 图3 形象化的布管形式 Fig.3 Visualizationoffreezingpipearrangement a网格划分 b温度云图(单位:℃) 图4 第3组网格划分及温度云图 Fig.4 Meshingfigureandtemperaturefield colormapofGroup3 从上述 4 组数值模拟和解析解的结果对比知 道,在工程常用的参数情况下,解析公式具有较高精 度,仅在冻结管处出现1 ℃左右的误差. a第1组 b第2组 c第3组 d第4组 图5 解析解计算结果与数值计算结果对比 Fig.5 Comparisonofanalyticaland numericalsolutions 398

390 同济大学学提(白然科学版) 第43卷 3.2与物理模型试验温度数据对比 名为3.45m,这与圈管冻结时,冻结圈内的冻土垢 由于采用双排广义布管形式的冻结工程较少 幕厚度大于园外的族土堆幕厚度是一致的,自此理 缺乏系统的温度监测数据,因此笔者采用双图管海 论公式需要的冻结管间距,冻结管排距,冻结管管半 结的物理模型试验温度监测数据与理论公式的计算 径、冻结管壁温度及冻土帷幕厚度均已知,可以根 结果进行对比,这能从一定程度上说明理论公式的 理论公式对己知测点的温度进行计算,其计算结果 实用性。 列于表3. 采用文献「191的物理模型试验数据进行对比 表31-1制面的8个测点温府及位置 其双圈管布置形式及温度测点如图6所示. Tab.3 Temperature and position of elght gp0 点 位置 2 250 -6.40 -65 0.1a 1.5 1.37 -12.0 -11.9 0. 112680 -1.37 -120 -11.80 0.20 567 -7.20 -7. 0.6 8-810 -200-1.70 0.30 15.0 考虑剖而2-2,坐标系选取原理与1-1剖面 致,则可知2-2剖面的1至8个测点位置与1-1剖面 的一样.另外面-2与面1-1的冻结参粉的推 区别在于第 排冻结管相对于第 排冻结管的偏移 困6冻结管及温度测点的分布(单位:m) 量心为(:/2,其余的理论公式需要的计算参数可直 Fig.6 Distribution of freezing pipe and 接使用1-1剖面的冻结参数.则22剂面的8个测点 measuring points (unit:m) 实测温度和理论计算温度加表4所示 本文将内图管当做第二推冻结管,外图管当做 ,2面的8个测点温度及位置 第一排冻结管,考虑的冻结温度曲线由5一25h(实 ad p 际对应时间30一150d,根据相似比将试验时间换算 measuring poi 为实际时间,后同)的5条,而不考虑后续的30~4( 点位置 实测理 h(180-240d)的3条族结曲线,因为前5条冻结曲 线的冻结管管壁温度是一样的.另外根据几何相似 比,可以将试验参数换算为实际参数,其且体布管形 1.37 -8.9 -8.86 0.0 式及相应的参数如表2所示 二10 表?冻结管布置参数 -6.80 -7.80 1.00 Tah 2 L 0 80 数值1.313 2.60.072-12 0 通过1-1剖面与2-2剖面的实测温度与理论温 考虑到理论公式的使用条件,即冻结中后期,则 度的对比可以看出.两者的临对误弟都不超过1℃ 选择25h(15 d的冻 温度分布曲线,考虑内图管 理论公式的精度满足工程上的误差要求,另外也说 与外圈管之间的中间位置作为直角坐标的原点,极 明利用理论公式估算冻士帷暮厚度精度较高 径方向作为y轴,向圆中心点的方向作为正方向,并 考虑横坐标x的取值水远为0.经量测可知1-1制面 4结论 的1至8个测点温度及位置如表3所示 根据测点1,3,5,7的实测温度和坐标值,依据 ()以特殊的单排管冻结温度场解析解为基 式(10)可以测算出冻土椎幕6为2.12m,冻土惟幕 础,将双排管冻结广义问题分解为两个特殊的单捕 1994-2015 China Academic Joumal Electronic Publishing House.All rights reserved.http:/www.cnkine
同 济 大 学 学 报(自 然 科 学 版) 第43卷 3.2 与物理模型试验温度数据对比 由于采用双排广义布管形式的冻结工程较少, 缺乏系统的温度监测数据,因此笔者采用双圈管冻 结的物理模型试验温度监测数据与理论公式的计算 结果进行对比,这能从一定程度上说明理论公式的 实用性. 采用文献[19]的 物 理 模 型 试 验 数 据 进 行 对 比. 其双圈管布置形式及温度测点如图6所示. 图6 冻结管及温度测点的分布(单位:m) Fig.6 Distributionoffreezingpipeand measuringpoints(unit:m) 本文将内圈管当做第二排冻结管,外圈管当做 第一排冻结管,考虑的冻结温度曲线由5~25h(实 际对应时间30~150d,根据相似比将试验时间换算 为实际时间,后同)的5条,而不考虑后续的30~40 h(180~240d)的3条冻结曲线,因为前5条冻结曲 线的冻结管管壁温度是一样的.另外根据几何相似 比,可以将试验参数换算为实际参数,其具体布管形 式及相应的参数如表2所示. 表2 冻结管布置参数 Tab.2 Layoutparametersoffreezingpipes 参数 l1/m l2/m L/m r0/m Tf/℃ T0/℃ 数值 1.31 3 2.6 0.072 -12 0 考虑到理论公式的使用条件,即冻结中后期,则 选择25h(150d)的冻结温度分布曲线,考虑内圈管 与外圈管之间的中间位置作为直角坐标的原点,极 径方向作为y轴,向圆中心点的方向作为正方向,并 考虑横坐标x的取值永远为0,经量测可知1-1剖面 的1至8个测点温度及位置如表3所示. 根据测点1,3,5,7的实测温度和坐标值,依据 式(10)可以测算出冻土帷幕ξ1 为2.12m,冻土帷幕 ξ2 为3.45m,这 与 圈管 冻 结 时,冻 结 圈 内 的 冻 土 帷 幕厚度大于圈外的冻土帷幕厚度是一致的.自此理 论公式需要的冻结管间距、冻结管排距、冻结管管半 径、冻结管壁温度及冻土帷幕厚度均已知,可以根据 理论公式对已知测点的温度进行计算,其计算结果 列于表3. 表3 1-1剖面的8个测点温度及位置 Tab.3 Temperatureandpositionofeight measuringpointsinSection1-1 测点 位置 y/m 实测温 度/℃ 理论温 度/℃ 绝对误 差/℃ 相对误 差/% 1 3.10 -4.70 -4.72 0.02 0 2 2.50 -6.40 -6.50 0.10 1.5 3 1.37 -12.00 -11.90 0.10 0.8 4 0.10 -9.60 -10.30 0.70 6.8 5 -1.37 -12.00 -11.80 0.20 1.7 6 -1.90 -7.20 -7.80 0.60 8.3 7 -2.50 -4.70 -4.70 0.00 0 8 -3.10 -2.00 -1.70 0.30 15.0 考虑 剖 面 2-2,坐标系选取原理与 1-1 剖 面 一 致,则可知2-2剖面的1至8个测点位置与1-1剖面 的一样,另外剖面2-2与剖面1-1的冻结参数的惟一 区别在于第二排冻结管相对于第一排冻结管的偏移 量w 为l2/2,其余的理论公式需要的计算参数可直 接使用1-1剖面的冻结参数.则2-2剖面的8个测点 实测温度和理论计算温度如表 4所示. 表4 2-2剖面的8个测点温度及位置 Tab.4 Temperatureandpositionofeight measuringpointsinSection2-2 测点 位置 y/m 实测温 度/℃ 理论温 度/℃ 绝对误 差/℃ 相对误 差/% 1 3.10 -5.00 -4.65 0.35 7.0 2 2.50 -6.40 -6.30 0.10 1.5 3 1.37 -8.90 -8.86 0.04 0.4 4 0.10 -9.60 -10.16 0.56 5.8 5 -1.37 -12.00 -11.80 0.02 0.2 6 -1.90 -6.80 -7.80 1.00 14.7 7 -2.50 -4.00 -4.70 0.70 17.5 8 -3.10 -2.00 -1.70 0.30 15.0 通过1-1剖面与2-2剖面的实测温度与理论温 度的对比可以看出,两者的绝对误差都不超过1 ℃, 理论公式的精度满足工程上的误差要求,另外也说 明利用理论公式估算冻土帷幕厚度精度较高. 4 结论 (1)以特殊的单排管冻结温度场解析解为 基 础,将双排管冻结广义问题分解为两个特殊的单排 309

第3期 胡向东,等:双持管冻结稳态温度场广义解析解 391 管冻结温度场问题,由此完成了双排广义解析解公 式.但公式必须在工程中常用的参数下使用(冻结中 Fp.013.57-20 后期,日1/L为0.510)使用 [11门湖向东,郭旺,张洛。无限大区城内少量冻结管稳态温度 (2)分别采用数值模拟和物理模型试验数据对 解析解的正确性进行了对比检验,解析解与数值解 几乎完全吻合,与物理模型试验实测数据吻合程度 in infinite.Journal of Chins Cosl Society.2013.38 也很高.表明了解析解的正确性, [12] D19 参考文献 HU Xiangdong.GUO Wang.ZHANG Luoyu.Analytical re field of four freezing pipe 1 Jiao Tong [2]户部帽。秋元政。谏士内湿度分布計算式上,专@吃用].冷 [3] 谏.1979.51(622):3. [1]HU Xiangdong.ZHANG Luoyu.Analytical soino ng University S013.186.06 ing in construction].Joumal of th [14]HU Xiangdong.ZHANG Luoyu.HAN Yanguang.An analytica n to temperature distribution of singl ns Division.1968.94 (SM1) 131 sture model of doubl [15]湖向东,汪洋.三挂管冻结温度场的势函数叠加法解析解 5)107 1333-1338. a of 考虑土层冻结温度时人工冻结湿度场 :日然科学板,20风 enng2012.31(5):1071 HU Xiangdong.HUANG Feng.BAI Nan.Models of artificial 16 ning and HU Xiangdong.SHE Siyuan.YU Ruizhi. [1门湖向东,陈,汪洋,等。环形单圈管陈结稳态温皮场解折 [1.岩士力学,2013,34(3)1874. [8]杨被,丁文其,潮向东,等。单排管冻士幕平均温度控制 HU Xiangdong.CHEN Jin,WANG Yang..Analyticn 数敏多性分析.地下空间与工程学报,2012,8(6):1208 2013.34(3):874 [18】陈想行,案铁虎,周忆.数学物理方程[M门.上海:复旦大学 Space and Eng 9] CHEN Sh HU Xiangdong.ZHAO Fei.SHE Siyuan.a Equivalent 200 olic arch oSocicty.2012,371):28. WANG Renhe.XU Shiliang.Modeling tet of tem state temperatur Teld ot one and two freezing pipes nea 1994-2015 China Academic Joural Electronic Publishing House All rights re http://www.cnki.ne
第3期 胡向东,等:双排管冻结稳态温度场广义解析解 管冻结温度场问题,由此完成了双排广义解析解公 式.但公式必须在工程中常用的参数下使用(冻结中 后期,且l/L 为0.5~1.0)使用. (2)分别采用数值模拟和物理模型试验数据对 解析解的正确性进行了对比检验,解析解与数值解 几乎完全吻合,与物理模型试验实测数据吻合程度 也很高.表明了解析解的正确性. 参考文献: [1] Трупак Н Г.Замораживаниегорных пород при проходке стволов[M].Москва:Углетехиздат,1954. [2] 戸部暢,秋元攻.凍土内温度分布計算式と,その応用[J].冷 凍,1979,54(622):3. [3] БахолдинБ В.Выбороптимальногорежимазамораживания грунтоввстроительныхцелях[M].Москва:Госстройиздат, 1963. [4] SangerFJ.Groundfreezinginconstruction[J].Journalofthe SoilMechanicsandFoundationsDivision,1968,94 (SM1): 131. [5] HU Xiangdong.Averagetemperature modelofdouble-row- pipefrozensoilwallbyequivalenttrapezoidmethod[C]∥AIP ConferenceProceedings.New York:AIPPublishing,2010: 1333-1338. [6] 胡向东,黄峰,白 楠.考虑土层冻结温度时人工冻结温度场 模型[J].中 国 矿 业 大 学 学 报:自 然 科 学 版,2008,37(4): 550. HU Xiangdong,HUANGFeng,BAINan.Modelsofartificial frozentemperaturefieldconsideringsoilfreezingpoint[J]. JournalofChinaUniversityof Mining&Technology:Natural Science,2008,37(4):550. [7 ] HU Xiangdong, SHE Siyuan, YU Ruizhi. Average temperaturecalculationforstraightsingle-row-pipedfrozensoil wall[J].SciencesinColdandAridRegions,2011,3(2):124. [8] 杨波,丁文其,胡向东,等.单排管冻土帷幕平均温度控制参 数敏感性分析[J].地下空间与工程学报,2012,8(6):1208. YANGBo,DING Wenqi,HU Xiangdong,etal.Sensitivity analysisofcontrolparametersforaveragetemperatureofsingle- row-pipefrozensoilwall[J].ChineseJournalofUnderground SpaceandEngineering,2012,8(6):1208. [9] 胡向东,赵飞,佘思源,等.直线双排管冻结壁平均温度的等 效抛物弓形模型[J].煤炭学报,2012,37(1):28. HU Xiangdong,ZHAO Fei,SHESiyuan,etal.Equivalent parabolicarch methodofaveragetemperaturecalculationfor straightdouble-row-pipefrozensoilwall[J].JournalofChina CoalSociety,2012,37(1):28. [10] HU Xiangdong,ZHANGLuoyu.Analyticalsolutiontosteady- statetemperaturefield ofoneandtwofreezing pipesnear linearadiabatic boundary[C]∥ 2013 Fourth International ConferenceonDigitalManufacturing&Automation.Qingdao: IEEECPS,2013:257-260. [11] 胡向东,郭旺,张 洛 瑜.无限大区域内少量冻结管稳态温度 场解析解[J].煤炭学报,2013,38(11):1953. HU Xiangdong,GUO Wang,ZHANG Luoyu.Analytical solutionofsteadystatetemperaturefieldofafewfreezingpipes ininfiniteregion[J].JournalofChinaCoalSociety,2013,38 (11):195. [12] 胡向东,郭旺,张 洛 瑜.无限大区域内四管冻结稳态温度场 解析解[J].上海交通大学学报,2013,47(9):1367. HU Xiangdong,GUO Wang,ZHANG Luoyu.Analytical solutionofsteadystatetemperaturefieldoffourfreezingpipes inan infiniteregion[J].Journalof ShanghaiJiao Tong University,2013,47(9):1367. [13] HU Xiangdong,ZHANGLuoyu.Analyticalsolutiontosteady- statetemperaturefieldoftwofreezingpipes with different temperatures[J].Journalof ShanghaiJiaotong University: Science,2013,18(6):706. [14] HU Xiangdong,ZHANGLuoyu,HAN Yanguang.Ananalytical solutiontotemperaturedistributionofsingle-row-pipedfreezing withdifferentpipesurfacetemperatures[J].AppliedMechanicsand Materials,2013(353/354/355/356):478. [15] 胡向 东,汪 洋.三排管冻结温度场的势函数叠加法解析解 [J].岩石力学与工程学报,2012,31(5):1071. HU Xiangdong,WANG Yang.Analyticalsolutionofthree- row- pipedfrozentemperaturefieldbymeansofsuperposition ofpotential[J].ChineseJournal of Rock Mechanicsand Engineering,2012,31(5):1071. [16] HUXiangdong,HANYanguang.Analyticalsolutiontosteady- statetemperaturefieldofasymmetricfrozensoilwallbysingle- row-pipefreezing[C]∥ 2013 International Conference on Materials, Architecture and Engineering Technology. Pennsylvania:DestechPublicationsInc,2013:636-641. [17] 胡向东,陈锦,汪洋,等.环形单圈管冻结稳态温度场解析解 [J].岩土力学,2013,34(3):874. HU Xiangdong,CHENJin,WANG Yang,etal.Analytical solutiontosteady-statetemperaturefieldofsingle-circle-pipe freezing[J].ChineseJournalof Rockand Soil Mechanics, 2013,34(3):874. [18] 陈恕行,秦铁虎,周忆.数学物理方程[M].上海:复旦大学 出版社,2003. CHEN Shuxing, QIN Tiehu, ZHOU Yi. Mathematical physicsequation[M ].Shanghai:Fudan University Press, 2003. [19] 汪仁和,徐士良.冻结壁温度场模型试验及其导热系数反分 析[J].安徽理工大学学报:自然科学版,2003,23(4):18. WANG Renhe,XU Shiliang.Modelingtestoftemperature fieldoffreezingwallandinverseheatconductionproblem[J]. Journalof Anhui University of Science and Technology: NaturalScience,2003,23(4):18. 193