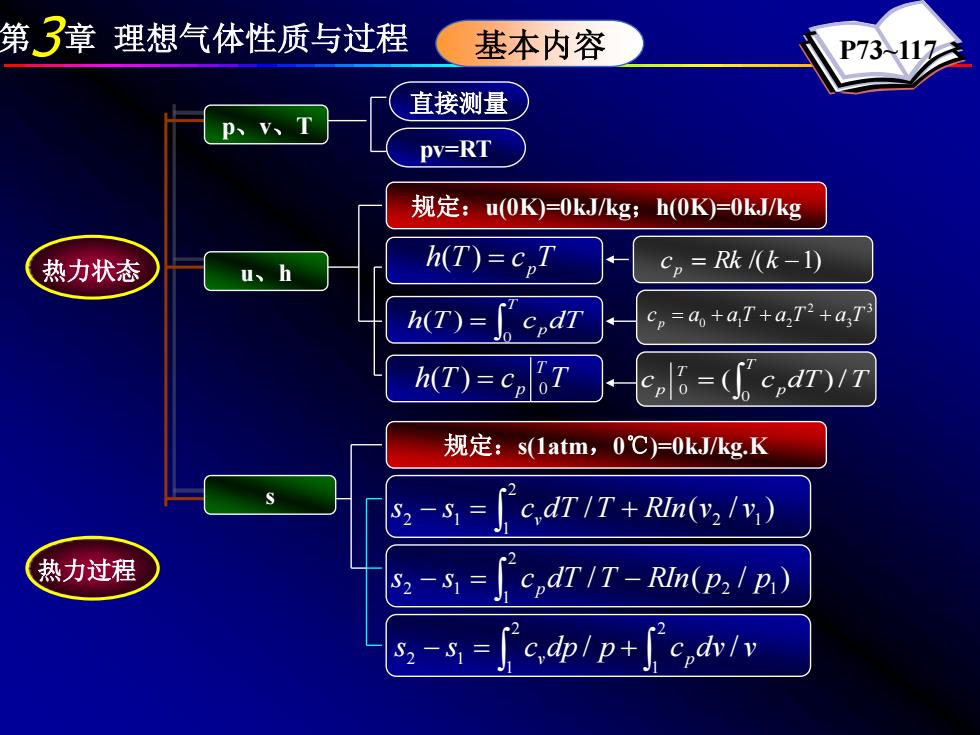
第3章理想气体性质与过程 基本内容 P73117 直接测量 p、v、T PV=RT 规定:u(0K=0kJkg; h(0K)=0kJ/kg 热力状态 u、h h(T)=c,T c。=Rkk-1) h(T)= a+aT+a,T2+a,T h(T)=c,T l=(c,dr)/7 规定:s(1atm,0℃)=0kJ/kg.K S2-S1= c,dT/T+RIn(v,/v) 热力过程 S2-S1= cpdT/T-RIn(p2/p) S2-S1= c,dplp+ c dv/y
第3章 理想气体性质与过程 P73~117 h(T) = c pT pv=RT ∫ = T h T c pdT 0 ( ) h T c TT p 0 ( ) = 3 3 2 c p = a0 + a1 T + a2T + a T / ( / ) 2 1 2 1 2 1 s s c dT T RIn v v − = v + ∫ c = Rk /(k −1) p c c dT T T p T p ( )/ 0 0 ∫ = / ( / ) 2 1 2 1 s2 − s1 = c pdT T − RIn p p ∫ ∫ ∫ − = + 2 1 2 1 2 1 s s c dp / p c dv / v v p 规定:u(0K)=0kJ/kg;h(0K)=0kJ/kg s 热力状态 热力过程 p、v、T u、h 直接测量 基本内容 规定:s(1atm,0℃)=0kJ/kg.K
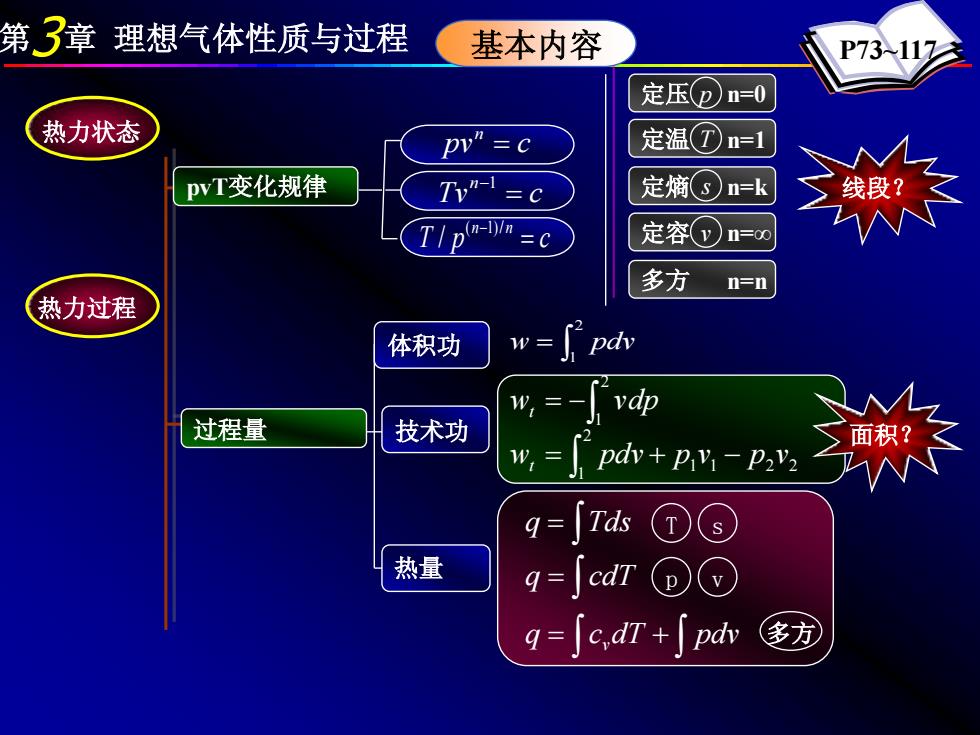
第3章理想气体性质与过程 基本内容 P73117 定压(p)n=0 热力状态 pw”=c 定温⑦n-1 pvT变化规律 Tv”=c 定熵(③n=k TI p(n-n =c 定容()n=∞ 多方 n=n 热力过程 体积功 vdp 过程量 技术功 W,= pav+pv-P2v2 q=∫Tds①s 热量 q=∫cdn⊙ q=c,dT+pdv 多方
第3章 理想气体性质与过程 P73~117 ∫ = 2 1 w pdv pv c n = Tv c n = −1 T p c n n = ( −1)/ / 定压 p n=0 定温 T n=1 定熵 s n=k 定容 v n=∞ 多方 n=n 线段? ∫ q = Tds ∫ q = cdT ∫ ∫ q = c dT + pdv v T s p v 多方 1 1 2 2 2 1 w pdv p v p v t = + − ∫ ∫ = − 2 1 wt vdp 热力状态 热力过程 基本内容 pvT变化规律 过程量 体积功 技术功 热量 面积?
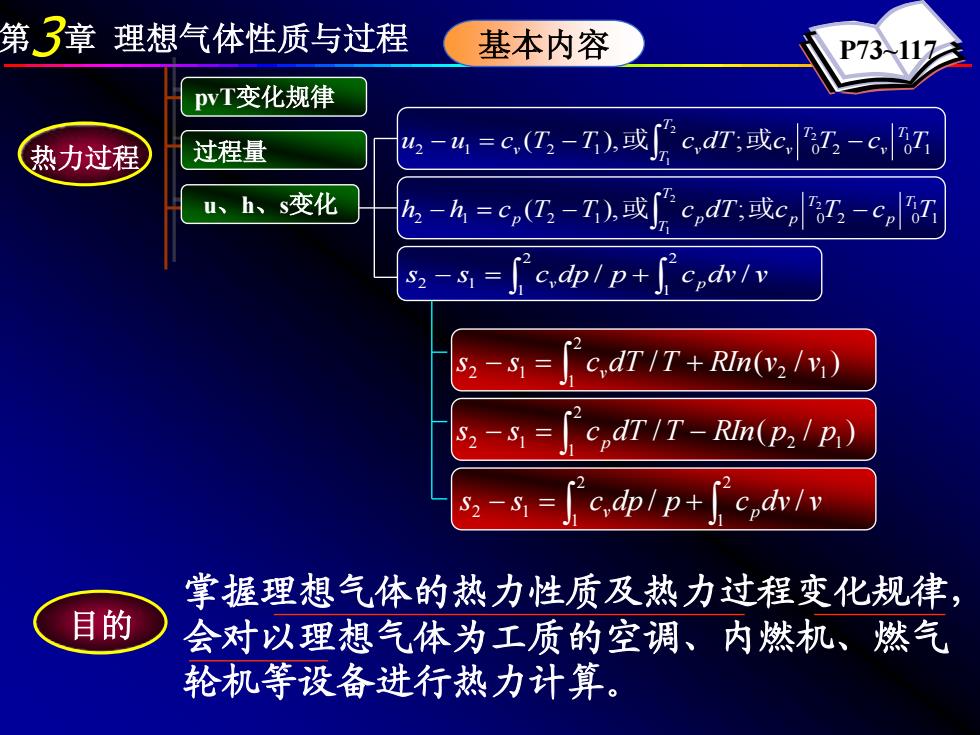
第3章理想气体性质与过程 基本内容 P73117 pvT变化规律 热力过程 过程量 42-4=c,(亿2-I,或c,dn;或c7-c7 u、h、s变化 h-h=c,(,-I),或cdΠ;或c,-c s2-s=c,pp+ cpdv/v 52-s [c,dT IT+RIn(v2) s2-s cpdTIT-RIn(p2I p) s2-s=c,dpl p+ c dv/v 掌握理想气体的热力性质及热力过程变化规律, 目的 会对以理想气体为工质的空调、内燃机、燃气 轮机等设备进行热力计算
第3章 理想气体性质与过程 基本内容 P73~117 2 1 2 1 0 2 0 1 2 1 2 1 u u c (T T ), c dT; c T c TT v T v T T − = v − v − 或∫ 或 ∫ ∫ − = + 2 1 2 1 2 1 s s c dp / p c dv / v v p 2 1 2 1 0 2 0 1 2 1 2 1 h h c (T T ), c dT; c T c TT p T p T T − = p − p − 或∫ 或 热力过程 pvT变化规律 过程量 u、h、s变化 / ( / ) 2 1 2 1 2 1 s s c dT T RIn v v − = v + ∫ / ( / ) 2 1 2 1 s2 − s1 = c pdT T − RIn p p ∫ ∫ ∫ − = + 2 1 2 1 2 1 s s c dp / p c dv / v v p 目的 掌握理想气体的热力性质及热力过程变化规律, 会对以理想气体为工质的空调、内燃机、燃气 轮机等设备进行热力计算

第3章理想气体性质与过程 基本内容 P73117 ①掌握理想气体的基本性质 要求 ②掌握理想气体热力过程变化规律及分析方 法(定量计算和定性分析)
第3章 理想气体性质与过程 基本内容 P73~117 要求 ①掌握理想气体的基本性质 ②掌握理想气体热力过程变化规律及分析方 法(定量计算和定性分析)

第3章理想气体性质与过程 P73入75 3-1理想气体状态方程 一理想气体(L.G.) 凡在任何温度、任何压力下均服从状态方程 pV=nRT的气体一理想气体 p:kPa,气体绝对压力 n:kmol,气体摩尔数 V:m3,气体体积 Ra: 通用气体常数 T:K, 热力学温度 8.314kJ/kmo1.K 每千克气体:pV=RT V:m3/kg,气体比容 R: 气体常数R=R/M=8.314/M,kJ/kg.K
第3章 理想气体性质与过程 P73~75 3-1理想气体状态方程 一.理想气体(I.G.) 凡在任何温度、任何压力下均服从状态方程 pV=nRmT的气体——理想气体 p:kPa,气体绝对压力 V:m3,气体体积 T:K,热力学温度 n:kmol,气体摩尔数 Rm:通用气体常数 8.314kJ/kmol.K v:m3/kg,气体比容 R:气体常数 R=Rm/M=8.314/M,kJ/kg.K 每千克气体:pv=RT

第3章理想气体性质与过程 P73入75 3-1理想气体状态方程 二状态方程 pV=c→ pdW+Vp=0→( 7一w(为n=0→ )p.n g=c一.a+-5m-0→ n P,7 n V=V(p,T,n) dv =
第3章 理想气体性质与过程 P73~75 3-1理想气体状态方程 二.状态方程 pV = c c T V = c n V = V =V ( p,T,n) p V p V pdV Vdp T n = − ∂ ∂ + = ⇒ , 0 ( ) T V T V dT T V dV T p n = ∂ ∂ + − 2 = ⇒ , ( ) 0 ( ) 1 n V n V dn n V dV n p T = ∂ ∂ + − 2 = ⇒ , ( ) 0 ( ) 1 dn n V dp p V dT T V dV p,n T ,n p,T ( ) ( ) ( ) ∂ ∂ + ∂ ∂ + ∂ ∂ =

第3章理想气体性质与过程 P7375 3-1理想气体状态方程 二状态方程 7++m -dn dv, dp dn PV=nR T 三理想气体物理模型 微观物理模型分子无大小;分子间无相互作用力
第3章 理想气体性质与过程 P73~75 3-1理想气体状态方程 二.状态方程 dn n V dp p V dT T V dV p,n T ,n p,T ( ) ( ) ( ) ∂ ∂ + ∂ ∂ + ∂ ∂ = dn n V dp p V dT T V dV = − + n dn T dT p dp V dV + = + ln( ) = 0 nT pV pV nR T d = m 三.理想气体物理模型 微观物理模型 分子无大小;分子间无相互作用力

第3章理想气体性质与计思 P7375 3-1理想气体状态方程 三理想气体物理模型 微观物理模型分子无大小;分子间无相互作用力 宏观物理模型p/=nRnT ①0.95<pv/RT<1.05。C0,02,H2,N2,以空气为 主的燃气等 程 近 ②三原子分子(H0,C0)一般不能当作理想气体, 似 但在混合气体中含量极少可以:空气中水蒸气;烟 气中C02等
第3章 理想气体性质与过程 P73~75 3-1理想气体状态方程 三.理想气体物理模型 微观物理模型 分子无大小;分子间无相互作用力 宏观物理模型 pV=nRmT ①0.95<pv/RT<1.05。CO,O2,H2,N2 ,以空气为 工 主的燃气等 程 近 似 ②三原子分子(H2O, CO2)一般不能当作理想气体, 但在混合气体中含量极少可以:空气中水蒸气;烟 气中CO2等

第3章理想气体性质与过程 P7577 3-2气体的比热容 计算内能,焓,热量都要用到热容 一.比热容 定义单位量的物质(无相变、无化学反应时)温度改 变1度需要的热量。 c=8qldT ①质量比热容C,kJ/kg.K 分类 ②摩尔比热容Cm,kJ/kmo1.K ③容积比热容C,kJ/m3(标态).K 关系 m =Mc=22.414C
第3章 理想气体性质与过程 P75~77 3-2 气体的比热容 一.比热容 定义 ①质量比热容c,kJ/kg.K 分类 单位量的物质(无相变、无化学反应时)温度改 变1度需要的热量。 ②摩尔比热容Cm,kJ/kmol.K ③容积比热容C’ ,kJ/m3 (标态).K Cm = Mc = 22.414C′ 关 系 c = δq / dT 计算内能, 焓, 热量都要用到热容

第3章理想气体性质与过程 P7577 3-2气体的比热容 根据过程不同,比热容分定容比热容和定压比热容。 二定压比热容、定容比热容 定压比热容cp cp =(8ql dT)p P=如g-冲 C, ,=导-西-,+0-4 定容比热容c, c,=(g/dT)
第3章 理想气体性质与过程 P75~77 3-2 气体的比热容 定压比热容cp 二.定压比热容、定容比热容 p q dT p c = (δ / ) 根据过程不同,比热容分定容比热容和定压比热容。 定容比热容cv δq = dh − vdp h = h(T, p) dp p h dT T h dh p T ( ) ( ) ∂ ∂ + ∂ ∂ = v dp p h dT T h q p T ( ) [( ) − ] ∂ ∂ + ∂ ∂ p p p δ = T h dT q c ( ) ( ) ∂ ∂ = = δ v v c = (δq / dT)