钢结构基本原理-04-受弯构件 2018/4/23 第一节概述 Introduction ©受力 第四章受弯构件 剪 分类: 平台梁、楼盖梁、吊车梁、檩条等 Flexural Members 主梁、次梁;单弯、双弯 简支、连续、悬膏 型钢、组合截面;等截面、变截面 2 ©截面形式(1)一型钢与组合截面 ©截面形式(2)一蜂窝梁 I C工C1T (a) (c) I 工 () () (d) G) ©截面形式(3)一变戴面梁、张弦梁等 国 ©受弯构件的极限状态 >强度破坏 第二节受弯构件的强度和刚度 >刚度不足 Strength and Stiffness >整体失稳 >局部失稳(屈曲) of Flexural Members 1
钢结构基本原理-04-受弯构件 2018/4/23 1 1 第四章 受弯构件 Flexural Members 2 第一节 概述 Introduction 受力: 弯,剪 分类: 平台梁、楼盖梁、吊车梁、檩条等 主梁、次梁; 单弯、双弯 简支、连续、悬臂 型钢、组合截面; 等截面、变截面 3 截面形式(1)-型钢与组合截面 4 截面形式(2)-蜂窝梁 截面形式(3)-变截面梁、张弦梁等 5 强度破坏 刚度不足 整体失稳 局部失稳(屈曲) 受弯构件的极限状态 6 第二节 受弯构件的强度和刚度 Strength and Stiffness of Flexural Members
钢结构基本原理-04-受弯构件 2018/4/23 2.1受弯构件的强度一抗弯 ©正应力发展过程 4阶段:弹性、弹塑性、塑性、应变硬化 ©弯矩一挠度关系 E=0 极限弯矩 设计?3 ©设计要求: 弹性:M=Wn∫ 矩形: 塑性:M,=Wm∫,=FWn∫ W =bh2/6 M,≤M.=yWn, y[1.0,F] 截面形状系数:F= W pn Won =bh2 /4 Mx≤f, rW F=1.5 截面形状系数F的取值: 矩形1.5,圆形1.7,圆管1.27, 工字形对x轴(强轴)1.10-1.17 10 2.2受弯构件的强度一抗剪 ⑧规范设计公式: 单弯 M.s5 ©剪应力分布 YWm 双弯 M+M,5 YW Y,W y取值: 工字形y=1.05,,=12 美B 箱形.05 12 2
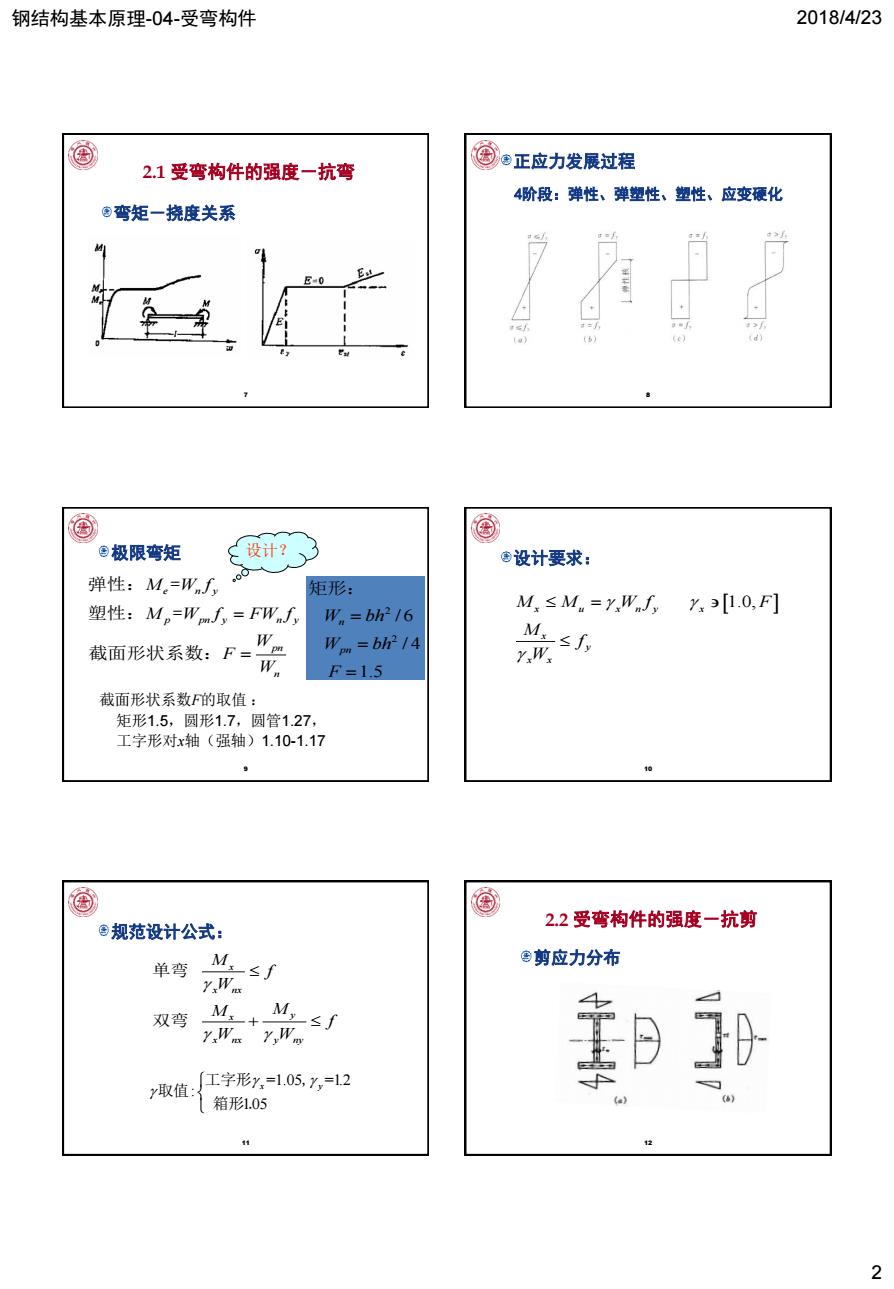
钢结构基本原理-04-受弯构件 2018/4/23 2 7 弯矩-挠度关系 2.1 受弯构件的强度-抗弯 8 正应力发展过程 4阶段:弹性、弹塑性、塑性、应变硬化 9 极限弯矩e n y p pn y n y pn n M W f M W f FW f W F W 弹性: = 塑性: = 截面形状系数: 截面形状系数F的取值 : 矩形1.5,圆形1.7,圆管1.27, 工字形对x轴(强轴)1.10-1.17 2 2 / 6 / 4 1.5 n pn W bh W bh F 矩形: 设计? 10 设计要求: x u x n y x 1.0, x y x x M M W f F M f W 11 规范设计公式:x x nx x y x nx y ny M f W M M f W W 单弯 双弯 =1.05 =1.2 : 105 x y 工字形 , 取值 箱形 . 12 剪应力分布 2.2 受弯构件的强度-抗剪
钢结构基本原理-04-受弯构件 2018/4/23 国 2.3受弯构件的强度一局部承压 ©规范公式 ©局部压应力力分布 S ≤∫ 轨道高 T= Itw 跨中集中荷载: 人=f/5 1.=a+5h,+2h 端支座反力处: 1=a+2.5h, 4 ©规范公式 2.4受弯构件的强度一多种应力组合 规范公式: 业F ≤f 弯剪组合 t Vo2+3x2≤1.1f ”:局部应力放大系数 弯剪局压组合 重级工作制吊车梁取135,其它取1.0 VG2+o-oo。+3x2≤Bf 为 1 国 2.5受弯构件的刚度 强度验算例题: 要求: 沈P152,例6-3,弯、剪、局部承压 表述与上课内容略有差异 v≤[ 请按课堂方法复算 v的计算:荷载标准值 [y的取值:使用要求,沈P384附表2.1 3
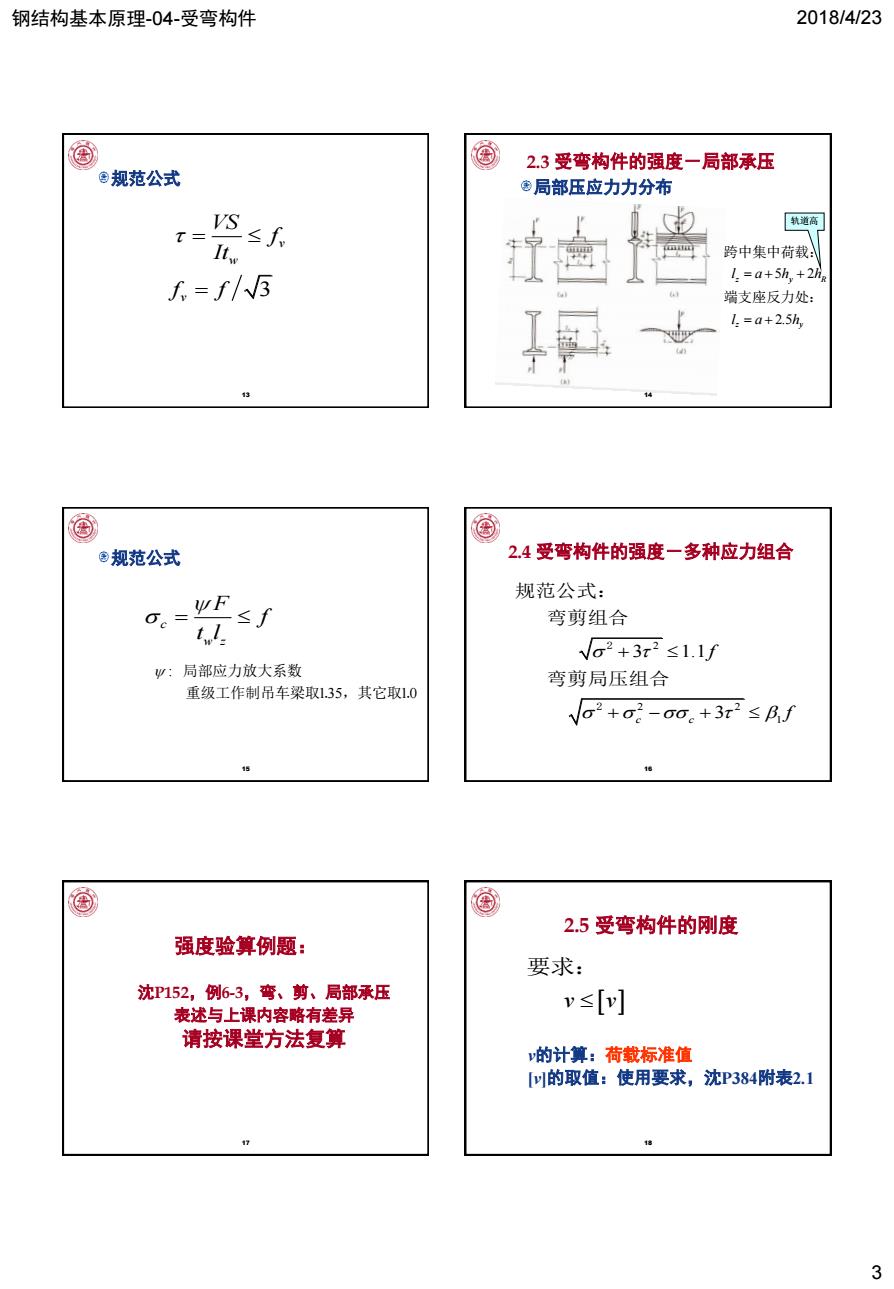
钢结构基本原理-04-受弯构件 2018/4/23 3 13 规范公式 3 v w v VS f It f f 14 局部压应力力分布 2.3 受弯构件的强度-局部承压 5 2 2.5 z y R z y l a h h l a h 跨中集中荷载: 端支座反力处: 轨道高 15 规范公式 c w z F f t l : 135 10 局部应力放大系数 重级工作制吊车梁取 . ,其它取 . 16 2.4 受弯构件的强度-多种应力组合 2 2 2 1 3 1.1 c c 3 f f 2 2 规范公式: 弯剪组合 弯剪局压组合 17 强度验算例题: 沈P152,例6-3,弯、剪、局部承压 表述与上课内容略有差异 请按课堂方法复算 18 2.5 受弯构件的刚度 v v 要求: v的计算:荷载标准值 [v]的取值:使用要求,沈P384附表2.1
钢结构基本原理-04-受弯构件 2018/4/23 国 @ 3.1梁的扭转 第三节受弯构件的整体稳定 OM. 自由扭转 (a》 Overall Stability 约束扭转 3.1.1自由扭转 ©开口薄壁截面: 矩形截面 (b>t) M、=GI,0=GI,p' M Tmax= 1. T NJ L,≈ (扭转常数或抗扭惯矩) 22 ®闭口薄壁截面: ©热轧型钢截面: 1-k2g 1=44/j5 3- k由试验确定,规范给出 4
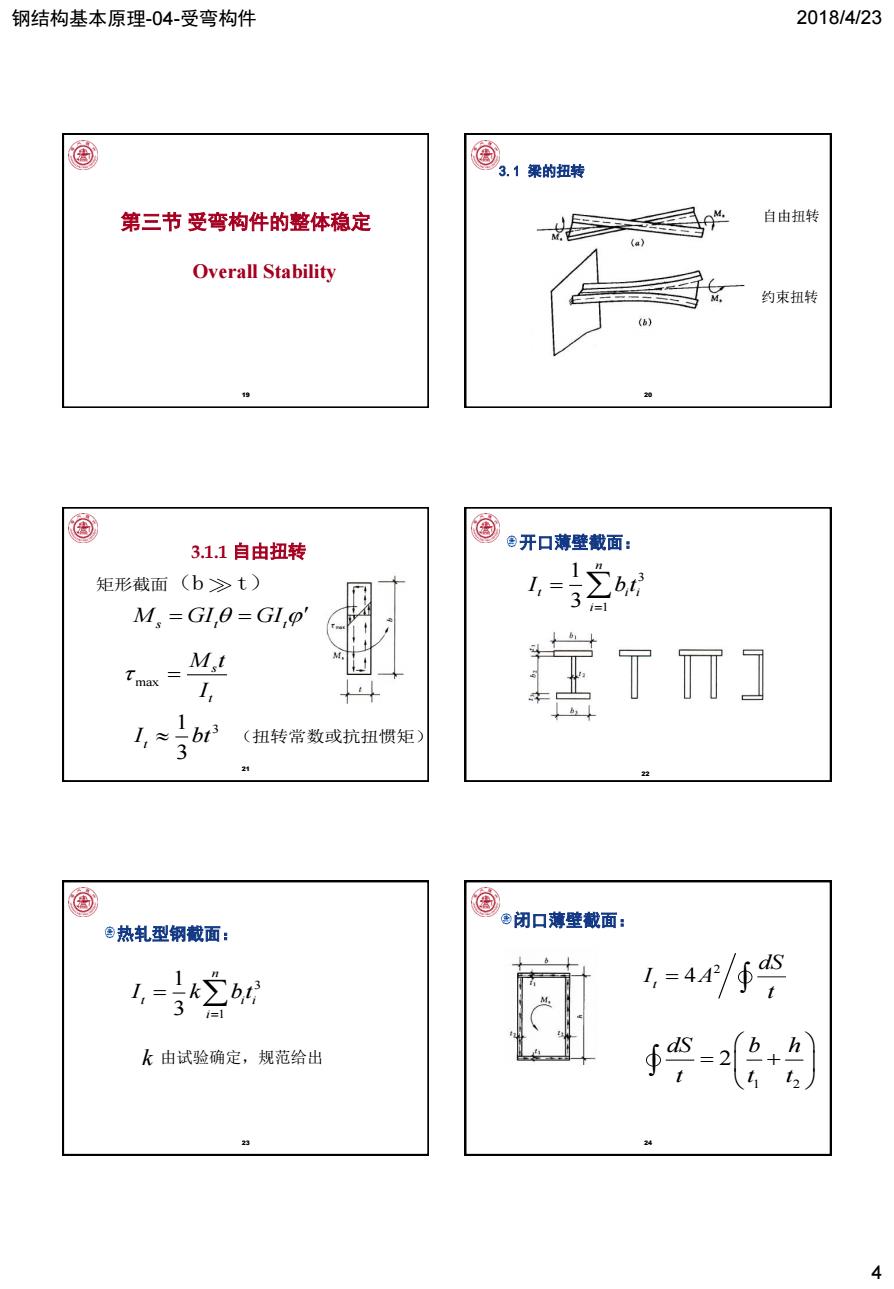
钢结构基本原理-04-受弯构件 2018/4/23 4 19 第三节 受弯构件的整体稳定 Overall Stability 20 3.1 梁的扭转 自由扭转 约束扭转 21 3.1.1 自由扭转 M GI GI s t t 矩形截面(b t) max 1 3 3 s t t M t I I bt (扭转常数或抗扭惯矩) 22 开口薄壁截面: 3 1 1 3 n t i i i I bt 23 热轧型钢截面: 3 1 1 3 n t i i i I k bt k 由试验确定,规范给出 24 闭口薄壁截面: 2 t 4 dS I A t 1 2 2 dS b h t t t

钢结构基本原理-04-受弯构件 2018/4/23 国。开口与闭口薄壁戴面扭转惯矩比较 3.1.2约束扭转 250 250 悬臂工字 12 开口/闭口=1:500 25 图剪应力分布 ©约束扭矩(1) Vi+dV T Mo=V h dM Vi= dMs dz My=-El du =-21 d'p m d? d (a) (b)- Mr=Ms+M ©约束扭矩(2) ©扭转平衡微分方程 M。=- El,hdp=-El。p" 2 ds Mr=Ms+M Ms=GI,p' Ih2 Io= 扇性惯矩 M=-ElPT 2 扇性贯矩一般计算复杂,可查手册 Mr=GI P'-EIo 30 5
钢结构基本原理-04-受弯构件 2018/4/23 5 开口/闭口=1:500 25 开口与闭口薄壁截面扭转惯矩比较 26 3.1.2 约束扭转 悬臂工字梁 27 剪应力分布 M M M T S 28 约束扭矩(1) M V h f 2 3 2 3 2 2 f f f f f f dM V dz d u h d M EI V EI dz dz h u 29 约束扭矩(2) 2 3 3 2 EI hf d M EI dz 2 2 f I h I 扇性惯矩 扇性贯矩一般计算复杂,可查手册 30 扭转平衡微分方程 M GI EI T t M M M T S M GI S t M EI
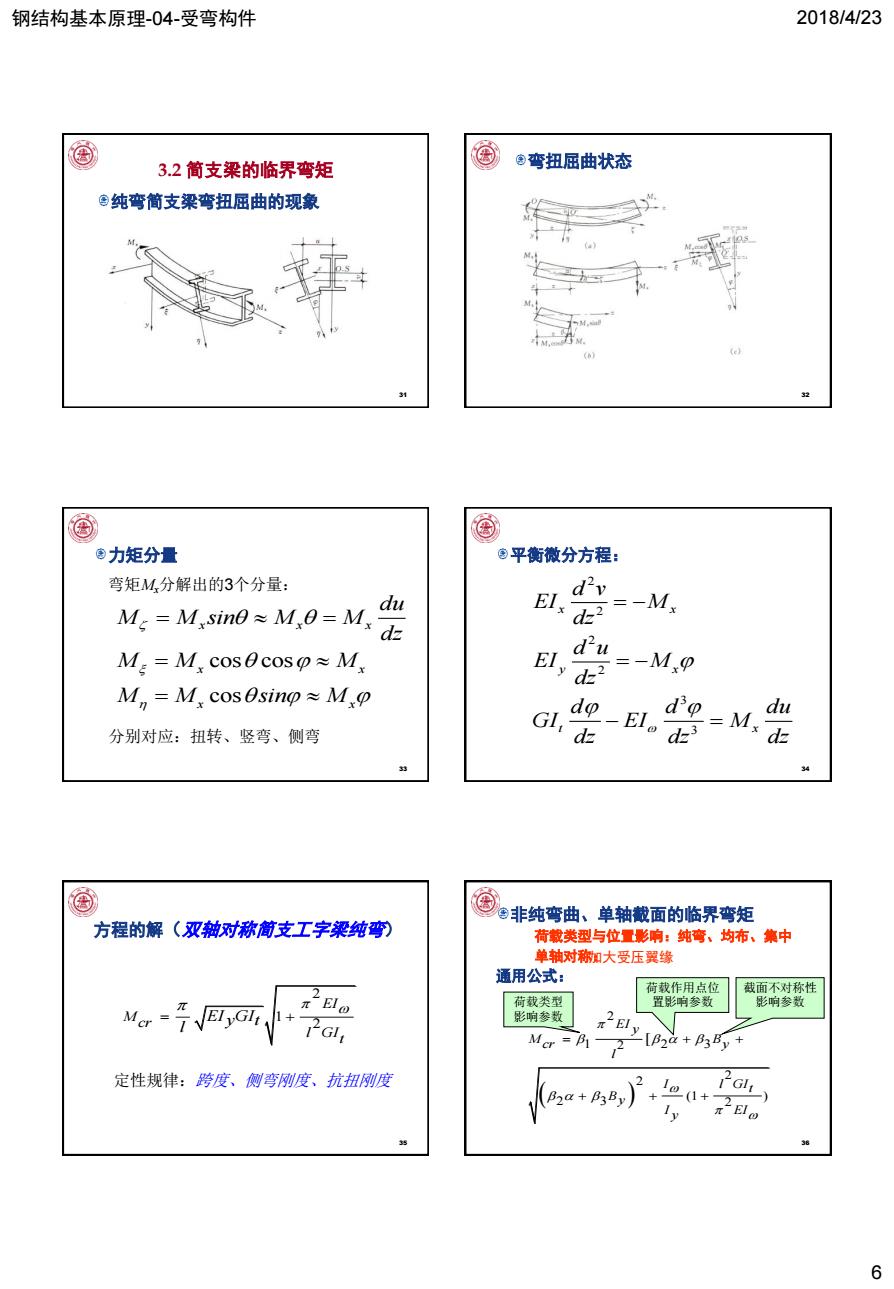
钢结构基本原理-04-受弯构件 2018/4/23 3.2简支梁的临界弯矩 粤弯扭屈曲状态 ©纯弯简支梁弯扭屈曲的现象 ®力矩分量 ©平衡微分方程: 弯矩M分解出的3个分量: dv M,=M,simb≈M,0=M,d正 du 2=-M M:=M,cos0coso≈Mx du de? --M.P M,=M,cos0sinp≈Mxp do do =M, du 分别对应:扭转、竖弯、侧弯 Gl:d dz 34 国 ©非纯弯曲、单轴戴面的临界弯矩 方程的解(双轴对称简支工字梁纯弯 荷载类型与位量影响:纯弯、均布、集中 单轴对称知大受压翼缘 通用公式: 荷载作用点位 截面不对称性 πElo 荷载类型 置影响参数 影响参数 影响参数 12GI Mcr =B 子+ 定性规律:跨度、侧弯刚度、抗扭刚度 B2a+B3By 19 6
钢结构基本原理-04-受弯构件 2018/4/23 6 31 3.2 简支梁的临界弯矩 纯弯简支梁弯扭屈曲的现象 32 弯扭屈曲状态 33 力矩分量 cos cos cos x x x x x x x du M M sin M M dz M M M M M sin M 弯矩Mx分解出的3个分量: 分别对应:扭转、竖弯、侧弯 34 平衡微分方程: 2 2 2 2 3 3 x x y x t x d v EI M dz d u EI M dz d d du GI EI M dz dz dz 35 方程的解(双轴对称简支工字梁纯弯) 2 1 2 EI Mcr l GIt EI GI y t l 定性规律:跨度、侧弯刚度、抗扭刚度 36 非纯弯曲、单轴截面的临界弯矩 荷载类型与位置影响:纯弯、均布、集中 单轴对称: 通用公式: 2 1 2 3 2 2 2 (1 ) 2 3 2 [ EI y M B cr y l I l GIt By I EI y 荷载作用点位 置影响参数 截面不对称性 荷载类型 影响参数 影响参数 加大受压翼缘

钢结构基本原理-04-受弯构件 2018/4/23 国 3.3整体稳定系数 国 3.3.1双轴对称工字梁、纯弯 Ocr= πEI W Mcr= →simplified 10.17×105 2 1+ 元y1 10.17×105 那 4.4h Ah + 4.4h 17 国 定义稳定系数 p。-cg 稳定系数表达式 ocr P= 稳定要求:M≤M.oro≤ocr f, M≤c-0,=,f 4320Ah (元y1 2 235 Design:= ● Wx YR YR w. 1+ 4.4h Mx≤∫ PW 3.3.2工字梁一般情况稳定系数表达式 ©工字梁一般情况稳定系数表达式 非纯弯、单轴对称一简化 荷载情况:纯弯与非纯弯 一般情况稳定系数表达式: 4320Ah 截面情况:单、双轴对称 P6=B。 弹塑性影响:应予考虑 诏所 元yl +nb 235 4.4h 42 7
钢结构基本原理-04-受弯构件 2018/4/23 7 37 3.3 整体稳定系数 3.3.1 双轴对称工字梁、纯弯 2 2 2 2 EI y I l GIt Mcr l I EI y y simplified 5 2 1 2 4.4 10.17 10 1 y Mcr t y Ah h 38 1 5 2 10.17 10 1 2 4.4 cr x x M cr W yt Ah W h y 39 Design = x b y b x R R x b x M f cr f W M f W : 定义稳定系数 b y cr f 稳定要求: cr or M M x cr 40 稳定系数表达式 1 2 4320 1 2 4.4 b y x cr f Ah yt W h y 235 y f 41 3.3.2 工字梁一般情况稳定系数表达式 荷载情况:纯弯与非纯弯 截面情况:单、双轴对称 弹塑性影响:应予考虑 42 工字梁一般情况稳定系数表达式 1 4320 2 2 235 1 4.4 b b x b y Ah W y yt h f 非纯弯、单轴对称→简化 一般情况稳定系数表达式:

钢结构基本原理-04-受弯构件 2018/4/23 国 国 3.3.3整体稳定的验算 弹塑性影响:比例极限∫。=0.6∫, (1)单向弯曲 when。>0.6, Mx≤f o p6'=1.07-0.2821p6≤1.0 (2)双向弯曲 M: Mysf ows rws 44 ©3.3.4稳定系数的实用简化(纯弯) T形截面: 轧制普通工字钢梁:查表 一般工字钢梁: 当1,≤120√P37 汤 双角钢:p。=1-0.0017入 V235 双轴对称:p。=1.07- 44000235 单轴对称:p。=1.07- 剖分与组合:P。=1-0.0022入 V235 等 Wis 诏 (2a6+0.1)Ah44000235 96 国 3.4不需验算整体稳定的条件 作业 >沈:P182:6.5(前支组合展,盛,非纳7 >陈:P164:4.18(衡支组合梁,蓝罐,非纯穷 (1)铺板 >用课堂方法,公式计算稳定系数 (2)工字形1,b,限值 (3)箱梁条件:尺寸 47 8
钢结构基本原理-04-受弯构件 2018/4/23 8 43 0.6, 1.07 0.282 / 1.0 b b b when 弹塑性影响:比例极限 f f p y 0.6 44 3.3.3 整体稳定的验算 (1)单向弯曲 (2)双向弯曲 x b x M f W x y b x y y M M f W W 45 3.3.4 稳定系数的实用简化(纯弯) 1 2 1.07 44000 235 1.07 2 2 0.1 44000 235 y b b x y b y f W y f Ah 双轴对称: 单轴对称: 轧制普通工字钢梁:查表 一般工字钢梁: 120 235 y y f 当 46 1 0.0017 235 1 0.0022 235 y b y y b y f f 双角钢: 剖分与组合: 等 T形截面: 47 3.4 不需验算整体稳定的条件 (1)铺板 (2)工字形l1 /b1限值 (3)箱梁条件:尺寸 48 作业 沈:P182:6.5 (简支组合梁、整稳、非纯弯) 陈:P164:4.18(简支组合梁、整稳、非纯弯) 用课堂方法,公式计算稳定系数

钢结构基本原理-04-受弯构件 2018/4/23 国 整体稳定的验算新旧规范比较 整体稳定的验算新旧规范比较 (1)B50017-2003(现行规苑) (2)GB50017-2017,即将执行 Mx M、 Pb形 ≤f PLr Wsf ≤1 P6=B。 4320Ah 子w (1-元6+8” 1n≤1.0 V+( 235 4.4h +17b 元b= yWf Mer 50 整体稳定的验算新旧规范比较 (2)GB50017-2017,即将执行 支的指酸和起始正刷化长运 费4行 量山更型 5 第四节受弯构件的局部稳定 四球结新 Local Buckling 热美塘时 日年一享形植周经压样的规度: A 上下翼成中到脑商 52 4.1翼缘板的局部稳定 与柱翼缘类似,限制宽厚比 宽厚比限值计算:与夏度要求关联 三边简支板弹性稳定: 要求:om≥0.95∫ Oonx =K 即: k含台s095 考虑弹塑性与弹性嵌固: 取: ∫=235可得: am=k万mEg)2 12(1-v2)(bJ 5 9
钢结构基本原理-04-受弯构件 2018/4/23 9 49 整体稳定的验算新旧规范比较 (1)GB50017-2003(现行规范) 1 4320 2 2 235 1 4.4 x b x b b x b y M f W Ah y W yt h f 50 整体稳定的验算新旧规范比较 1/ 2 2 0 1 1 1.0 1 x b x x b n n n b b x x b cr M W f W f M (2)GB50017-2017,即将执行 51 整体稳定的验算新旧规范比较 (2)GB50017-2017,即将执行 52 第四节 受弯构件的局部稳定 Local Buckling 53 4.1 翼缘板的局部稳定 与柱翼缘类似,限制宽厚比 2 2 2 12 1 crx E t K v b 三边简支板弹性稳定: 2 2 2 12 1 crx E t K v b 考虑弹塑性与弹性嵌固: 54 宽厚比限值计算:与强度要求关联 2 2 2 0.95 0.95 12 1 =235 15 crx y y y f E t K f v b b f t 要求: 即: 取: 可得:

钢结构基本原理-04-受弯构件 2018/4/23 4.2腹板的局部稳定 准则o。≥0.955→4s15 235 与五开和微 准则:部分塑性三么≤13 235 t 准则: 全塑性一b≤9 235 235 56 4.2腹板的局部稳定 4.2.1腹板区格各受力状况的稳定 ©加劲肋的设置 粤纯弯 国腹板区格的受力状况: 纯弯、纯剪、局部承压、联合作用 国 窗©临界应力 纯弯理论公式: 两边简支 两边嵌固 四边简支板: X=39.6/23.9=1.66 -) π2E Oer =K 四边简支 考虑弹性嵌固: 四边简支: K) Xπ2E -445 5 60 10
钢结构基本原理-04-受弯构件 2018/4/23 10 55 1 235 cr y 0.95 15 y b f t f 准则 1 235 13 y b t f 准则:部分塑性 1 235 9 y b t f 准则:全塑性 235 k y f 56 4.2 腹板的局部稳定 与压杆相同做 法? 57 4.2 腹板的局部稳定 加劲肋的设置 腹板区格的受力状况: 纯弯、纯剪、局部承压、联合作用 58 4.2.1 腹板区格各受力状况的稳定 纯弯 59 纯弯理论公式: 2 2 2 12 1 0 w crx E t K v h 四边简支板: 2 2 2 12 1 0 w crx E t K v h 考虑弹性嵌固: 60 临界应力 2 0 100 445 w cr t h 四边简支: 四边简支 =39.6/23.9=1.66 两边简支、 两边嵌固