
2017第二季度 网络课堂 屈曲分析 主讲人:陈辉
屈曲分析 主讲人:陈 辉 2017第二季度 网络课堂
结构稳定问题的相关理论 目录 屈曲分析在midas Gen中的实现 CONTENT 屈曲分析常见问题
CONTENT 目录 屈曲分析在midas Gen中的实现 屈曲分析常见问题 结构稳定问题的相关理论

结构稳定问题 基本理论 ·稳定性的基本概念 ·结构失稳类型及计算方法 。 线性屈曲分析与非线性屈曲分析
• 稳定性的基本概念 结构稳定问题 1 基本理论 • 结构失稳类型及计算方法 • 线性屈曲分析与非线性屈曲分析 • 稳定性的基本概念
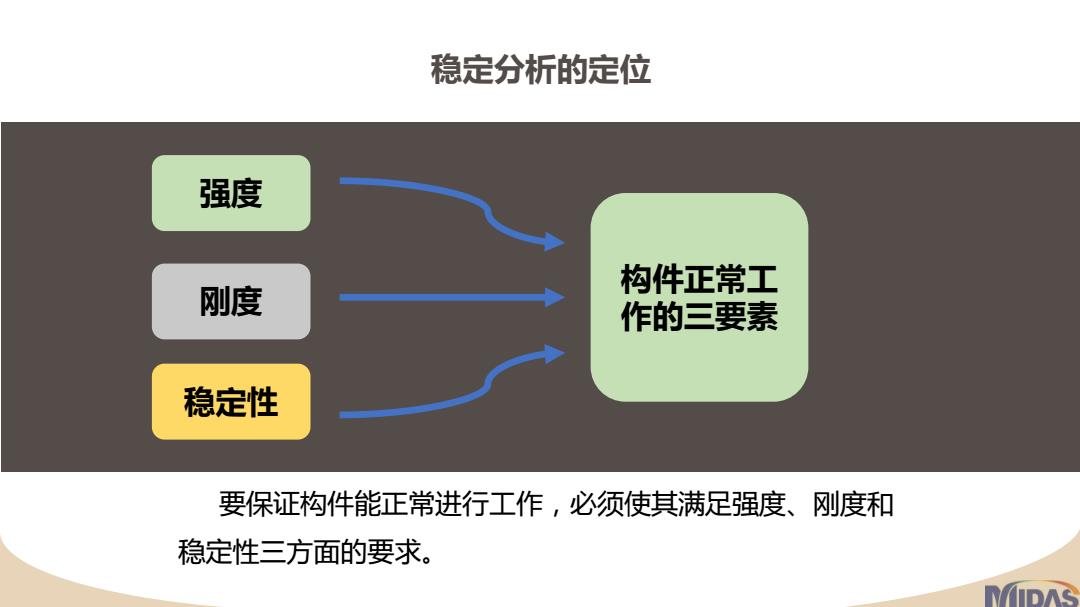
稳定分析的定位 强度 刚度 构件正常工 作的三要素 稳定性 要保证构件能正常进行工作,必须使其满足强度、刚度和 稳定性三方面的要求。 DAS
稳定分析的定位 要保证构件能正常进行工作,必须使其满足强度、刚度和 稳定性三方面的要求。 强度 刚度 稳定性 构件正常工 作的三要素

稳定分析的定位 强度问题 结构或构件在荷载作用下抵抗破坏的能力。 稳定问题 结构或构件在荷载作用下保持原有平衡状态的能力。 建筑结构分析中两类问题
稳定分析的定位 强度问题 稳定问题 建筑结构分析中两类问题 结构或构件在荷载作用下抵抗破坏的能力。 结构或构件在荷载作用下保持原有平衡状态的能力
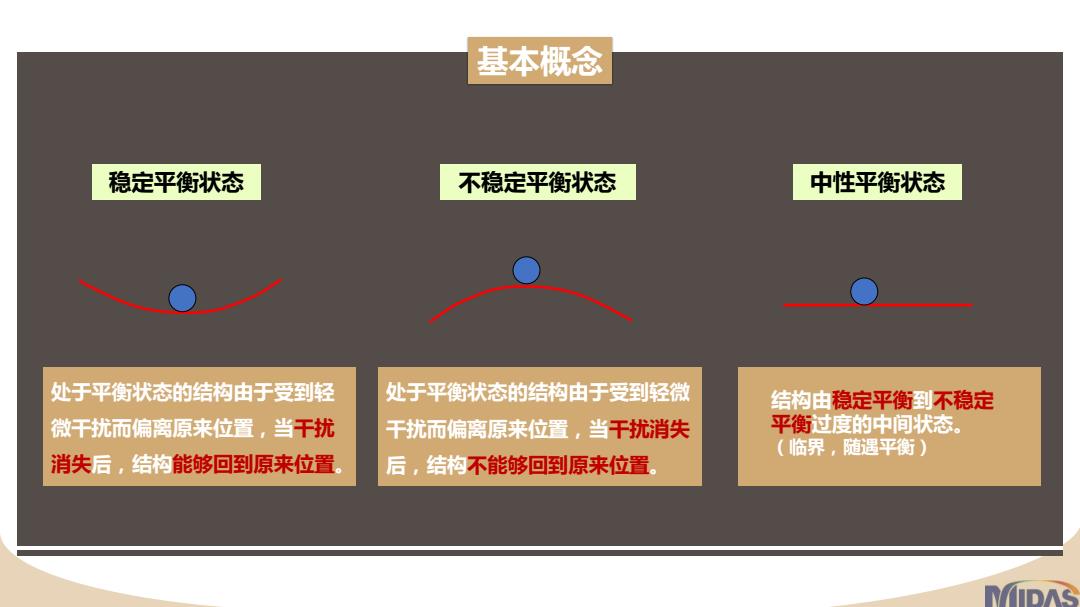
基本概念 稳定平衡状态 不稳定平衡状态 中性平衡状态 处于平衡状态的结构由于受到轻 处于平衡状态的结构由于受到轻微 结构由稳定平衡到不稳定 微干扰而偏离原来位置,当干扰 干扰而偏离原来位置,当干扰消失 平衡过度的中间状态。 (临界,随遇平衡) 消失后,结构能够回到原来位置。 后,结构不能够回到原来位置
基本概念 稳定平衡状态 处于平衡状态的结构由于受到轻 微干扰而偏离原来位置,当干扰 消失后,结构能够回到原来位置。 不稳定平衡状态 处于平衡状态的结构由于受到轻微 干扰而偏离原来位置,当干扰消失 后,结构不能够回到原来位置。 中性平衡状态 结构由稳定平衡到不稳定 平衡过度的中间状态。 (临界,随遇平衡)

基本概念 结构失稳(屈曲) 随着荷载的逐渐增大,结构的原始平衡位置由稳定平衡转为不稳定平衡 结构丧失其稳定性。 河南安阳某脚手架整体坍塌 马来西亚体育场半边垮塌 ■ 《空间网格结构技术规程》JG)7-2010中4.3.1条: 上海某住宅楼整体垮塌 单层网壳以及厚度小于跨度1/50的双层网壳均应进 行稳定性计算
基本概念 结构失稳(屈曲) 随着荷载的逐渐增大,结构的原始平衡位置由稳定平衡转为不稳定平衡。 结构丧失其稳定性。 《空间网格结构技术规程》JGJ7-2010中4.3.1条: 单层网壳以及厚度小于跨度1/50的双层网壳均应进 行稳定性计算。 上海某住宅楼整体垮塌 河南安阳某脚手架整体坍塌 马来西亚体育场半边垮塌

结构稳定问题 基本理论 ·稳定性的基本概念 ·结构失稳类型及计算方法 。 线性屈曲分析与非线性屈曲分析
• 稳定性的基本概念 结构稳定问题 1 基本理论 • 结构失稳类型及计算方法 • 线性屈曲分析与非线性屈曲分析 • 稳定性的基本概念
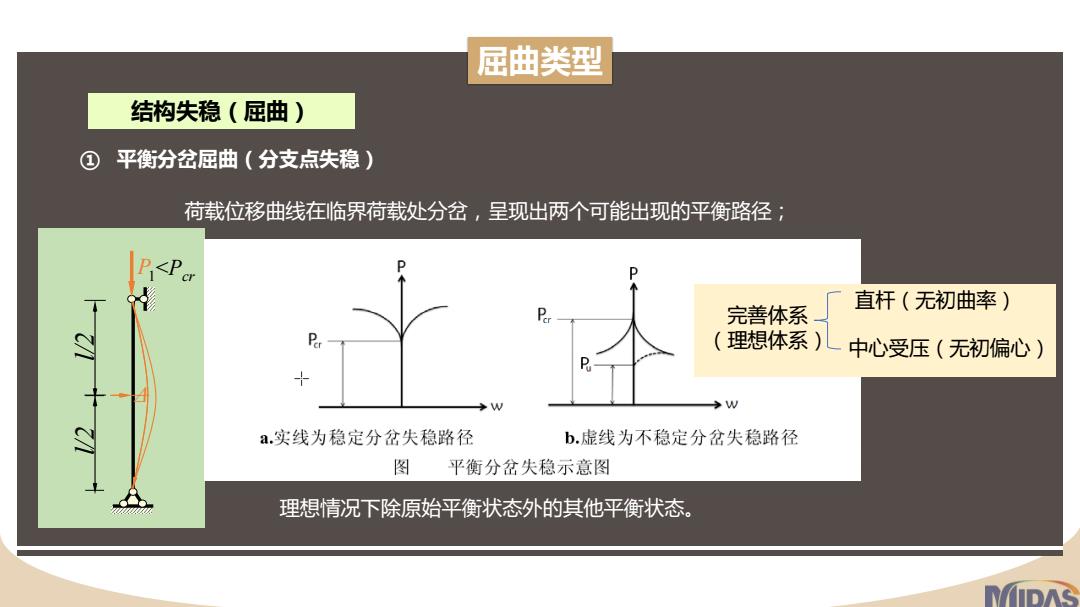
屈曲类型 结构失稳(屈曲) ① 平衡分岔屈曲(分支点失稳) 荷载位移曲线在临界荷载处分岔,呈现出两个可能出现的平衡路径: 完善体系 直杆(无初曲率) P 理想体系)儿 中心受压(无初偏心) W a.实线为稳定分岔失稳路径 b.虚线为不稳定分岔失稳路径 图 平衡分岔失稳示意图 理想情况下除原始平衡状态外的其他平衡状态
屈曲类型 结构失稳(屈曲) ① 平衡分岔屈曲(分支点失稳) 荷载位移曲线在临界荷载处分岔,呈现出两个可能出现的平衡路径; P l/2 l/2 1<Pcr Δ 理想情况下除原始平衡状态外的其他平衡状态。 完善体系 (理想体系) 直杆(无初曲率) 中心受压(无初偏心)

屈曲类型 结构失稳(屈曲) ②极值点失稳(非稳定分岔屈曲) 具有初曲率的压杆 非完善体系 承受偏心荷载的压杆 接近失稳时,荷载增量很小,挠度迅速增加。 曲线存在最高点,不会出现变形状态分岔,结 P (大挠度理论) 构变形的性质始终如一(结构平衡状态不会发 4 生质的变化)。 需要考虑结构材料弹塑性、几何非线性等特性
屈曲类型 结构失稳(屈曲) ② 极值点失稳(非稳定分岔屈曲) 接近失稳时,荷载增量很小,挠度迅速增加。 曲线存在最高点,不会出现变形状态分岔,结 构变形的性质始终如一(结构平衡状态不会发 生质的变化)。 P O Δ Pcr (大挠度理论) P e 需要考虑结构材料弹塑性、几何非线性等特性。 非完善体系 具有初曲率的压杆 承受偏心荷载的压杆