
Non-Uniform Recursive Doo-Sabin Surfaces Zhangjin Huang'Guoping Wang University of Science and Technology of China Peking University,China SIAM Conference on Geometric and Physical Modeling ZHuang G Warg Nen-U ho
Non-Uniform Recursive Doo-Sabin Surfaces Zhangjin Huang1 Guoping Wang2 1University of Science and Technology of China 2Peking University, China SIAM Conference on Geometric and Physical Modeling Z Huang, G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)

Doo-Sabin Surfaces Generalization of uniform biquadratic B-spline surfaces to meshes of arbitrary topology [Doo and Sabin 1978]. Limit point rule:For an n-sided face, its centroid is the limit position of its associated extraordinary point. The extraordinary points are at the "centers"of n-sided faces. Convergence:The Doo-Sabin refinement is convergent for extraordinary points with arbitrary valence. Z Huang.G Wang Non-Uniform Recursive Doo-Sabin Surtaces (NURDSes)
Doo-Sabin Surfaces Generalization of uniform biquadratic B-spline surfaces to meshes of arbitrary topology [Doo and Sabin 1978]. Limit point rule: For an n-sided face, its centroid is the limit position of its associated extraordinary point. The extraordinary points are at the "centers" of n-sided faces. Convergence: The Doo-Sabin refinement is convergent for extraordinary points with arbitrary valence. Z Huang, G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)

Quadratic NURSSes Generalization of non-uniform biquadratic B-spline surfaces to meshes of arbitrary topology [Sederberg et al.1998]. No closed form limit point rules. Converge for n-sided faces with n<12,but may diverge if n 12 [Qin et al.1998]. Z Huang.G Wang Non-Uniform Recursive Doo-Sabin Surtaces (NURDSes)
Quadratic NURSSes Generalization of non-uniform biquadratic B-spline surfaces to meshes of arbitrary topology [Sederberg et al. 1998]. No closed form limit point rules. Converge for n-sided faces with n ≤ 12, but may diverge if n > 12 [Qin et al. 1998]. Z Huang, G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)

Doo-Sabin Subdivision n-1 p=>wP,i=0,n-1. j=0 Doo-Sabin version [Doo and Sabin 1978],extended to quadratic NURSS: i=j 3+2cos(2m-1/D,i≠j 4n Catmull-Clark variant [Catmull and Clark 1978]: 是+动,i-引=0 +,i-引=1 i-引>1 Z Huang.G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)
Doo-Sabin Subdivision Pi = Xn−1 j=0 wijPj , i = 0, . . . , n − 1. Doo-Sabin version [Doo and Sabin 1978], extended to quadratic NURSS: wij = ( n+5 4n , i = j 3+2 cos(2π(i−j)/n) 4n , i 6= j Catmull-Clark variant [Catmull and Clark 1978]: wij = 1 2 + 1 4n , |i − j| = 0 1 8 + 1 4n , |i − j| = 1 1 4n , |i − j| > 1 Z Huang, G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)

Catmull-Clark Variant of Doo-Sabin Subdivision Repeated averaging [Stam 2001,Zorin and Schroder 2001]: ■Linear subdivision: E,=B,+P+小 ■Dual averaging: E=R+E-1+B+) =(2+4 P++P+1+P)t∑ Z Huang.G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)
Catmull-Clark Variant of Doo-Sabin Subdivision Repeated averaging [Stam 2001, Zorin and Schröder 2001]: Linear subdivision: Ei = 1 2 (Pi + Pi+1), F = 1 n Xn−1 j=0 Pj Dual averaging: Pi = 1 4 (Pi + Ei−1 + Ei + F) = (1 2 + 1 4n )Pi + (1 8 + 1 4n )(Pi+1 + Pi−1) + 1 4n X |i−j|>1 Pj . Z Huang, G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)

Non-uniform Quadratic B-spline Subdivision Non-uniform Quadratic B-spline Curves P knot intervals:d-1 ddi+i knots::-4.8+14+2 For a quadratic B-spline curve,a knot interval di is assigned to each control point P;. A knot interval is the difference between two adjacent knots in the knot vector,i.e.,the parameter length of a B-spline curve segment. ZHuang.G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)
Non-uniform Quadratic B-spline Subdivision Non-uniform Quadratic B-spline Curves For a quadratic B-spline curve, a knot interval di is assigned to each control point Pi . A knot interval is the difference between two adjacent knots in the knot vector, i.e., the parameter length of a B-spline curve segment. Z Huang, G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)

Non-uniform Quadratic B-spline Subdivision Non-uniform Quadratic B-spline Subdivision Refinement rules E Repeated averaging: Non-uniform linear subdivision: E=ditiPi+diPit di+di+1 ■Averaging: Q=e,+E)=a+24P,+dP+ 2(d+d+1) Q2+1=2+1+E)= d+1Pi+(2d+d+1)Pi+1 2(di dith).,.,至pac Z Huang.G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)
Non-uniform Quadratic B-spline Subdivision Non-uniform Quadratic B-spline Subdivision Refinement rules Repeated averaging: Non-uniform linear subdivision: Ei = di+1Pi + diPi+1 di + di+1 Averaging: Q2i = 1 2 (Pi + Ei) == (di + 2di+1)Pi + diPi+1 2(di + di+1) Q2i+1 = 1 2 (Pi+1 + Ei) = di+1Pi + (2di + di+1)Pi+1 2(di + di+1) . Z Huang, G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)
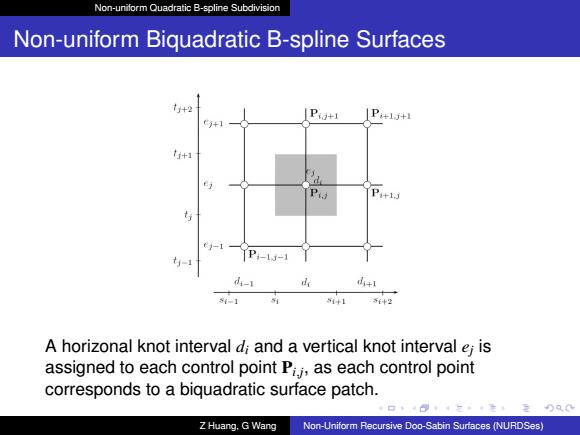
Non-uniform Quadratic B-spline Subdivision Non-uniform Biquadratic B-spline Surfaces +2 P+1 P+1+1 +1 -1 t-1 P-1J-1 d-1 d +1 1 +1 A horizonal knot interval di and a vertical knot interval e;is assigned to each control point Pi as each control point corresponds to a biquadratic surface patch. ZHuang.G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)
Non-uniform Quadratic B-spline Subdivision Non-uniform Biquadratic B-spline Surfaces A horizonal knot interval di and a vertical knot interval ej is assigned to each control point Pi,j , as each control point corresponds to a biquadratic surface patch. Z Huang, G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)

Non-uniform Quadratic B-spline Subdivision Non-uniform Biquadratic B-spline Subdivision Refinement rules Repeated averaging: Non-uniform linear subdivision: E=+,=9#B+sB出 di+diti ej+ejtl F=i(ditiPij+dPitij)+e(diPiti+dPij) (d+d+i)(e+ei+1) Dual averaging:Q2i.2j=(Pij +E1+E2+F) 。生 Z Huang.G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)
Non-uniform Quadratic B-spline Subdivision Non-uniform Biquadratic B-spline Subdivision Refinement rules Repeated averaging: Non-uniform linear subdivision: E1 = di+1Pi,j + diPi+1,j di + di+1 , E2 = ej+1Pi,j + ejPi,j+1 ej + ej+1 F = ej+1(di+1Pi,j + diPi+1,j) + ej(di+1Pi,j+1 + diPi+1,j+1) (di + di+1)(ej + ej+1) Dual averaging: Q2i,2j = 1 4 (Pi,j + E1 + E2 + F) Z Huang, G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)

NURDSes Non-uniform Doo-Sabin Surfaces Each vertex is assigned a knot interval(possibly different)for each edge incident to it. After subdivision,new knot intervals can be specified as follows: 配+1=1=论+1 -1=站+1=- Z Huang,G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)
NURDSes Non-uniform Doo-Sabin Surfaces Each vertex is assigned a knot interval (possibly different) for each edge incident to it. After subdivision, new knot intervals d¯k ij can be specified as follows: d¯0 i,i+1 = d¯−1 i,i−1 = d 0 i,i+1 d¯0 i,i−1 = d¯1 i,i+1 = d 0 i,i−1 . Z Huang, G Wang Non-Uniform Recursive Doo-Sabin Surfaces (NURDSes)