
S9.3.2B-树 §9.3.2B-树 1景老 ■定义:一裸m(m≥3)阶的B制是清足下述性质的m叉制: ·B是一种完全平衡的多阶找,主要是作为盘文并的引组织,用于 s性质1:每个轴点至少包含下列放据媒:0,P。,K,P,K2…,K,P】 外都查找, j:keys总数,K:关输字,P:指针 ■燕本想法是增大结点来韩低树高,减少访问外存的次数 keys(Po)ptr0 1
1 1 § 9.3.2 B-树 1.概念 B-树是一种完全平衡的多阶查找树,主要是作为磁盘文件的索引组织,用于 外部查找。 基本想法是增大结点来降低树高,减少访问外存的次数 一棵m阶B-树,每个结点最多有m个孩子,m一般为50-2000 例如,1棵1001阶B-树,3层即可包含10亿以上的Keys,当根结点置于内存 时,查找任一Key至多只要访问2次外存。 1000 1000 1000 1000 1000 1000 … 1001 … 1001 … 1001 1个结点 1000个关键字 1001个结点 1,001,000个关键字 1,002,001个结点 1,002,001,000个关键字 2 § 9.3.2 B-树 定义:一棵m(m≥3)阶的B-树是满足下述性质的m叉树: 性质1:每个结点至少包含下列数据域:(j, P0, K1, P1, K2, … , Kj , Pj ) j:keys总数, Ki :关键字, Pi :指针 keys(P0) ptr[0];

◆若key0kKptri]: {p=q;q->key[0]=K;严设置查找哨兵1 ◆若Kkey[keynum]:T-T->ptr[keynum: for (n=g->keynum Kkey[n];n-) 转①,直到T是叶子结点且未找到相等的关键字,则 if (n>0&&EQ(q->key[n].K))return n 查找失败。 q=q->ptr[n] (②算法实现 } retum 0; int BT_search(BTNode*T,KeyType K,BTNode*p) } 严在B树中查找关键字K查找成功返回在结点中的位置 严及结点指针p:香则返回0及最后一个结点指针) (3)算法分析 {BTNode *g;int n; 在B树上的查找有两中基本操作: p=q=T: ◆在B树上查找结点(查找算法中没有体现): ◆在结点中查找关键字:在磁盘上找到指针ptr所指 因此有:h1+8.(+1)/2=1+gm21(+1)2) 向的结点后,将结点信息读入内存后再查找。因此, 即在含有个关键字的B树上进行查找时,从根结 磁盘上的查找次数(待查找的记录关键字在B树上的 点到待查找记录关键字的结点的路径上所涉及的结点数 层次数)是决定B树查找效率的首要因素。 不超过1+gm2(+1)/2)。 根据m阶B树的定义,第一层上至少有1个结点, 第二层上至少有2个结点:除根结点外,所有非终端结 点至少有m/2棵子树,.,第h层上至少有mv22个 结点。在这些结点中:根结点至少包含1个关键字,其 它结点至少包含m/2-1个关键字,设s=m/2,则总的 关键字数目n满足: n≥1+s-1)22s2=1+20s-11=2s11 2 s-1 3B树的插入 (2)结点“分裂”方法 B树的生成也是从空树起,逐个插入关键字。插 设待“分裂”结点包含信息为: 入时不是每插入一个关键字就添加一个叶子结点,而是 首先在最低层的某个叶子结点中添加一个关键字,然后 (m,AgK,A,K2,A2,…KmA,从其 有可能“分裂”。 中间位置分为两个结点: (m21,Ag,K,A1,.,Kmw21,4m2i) ()插入思想 (m-m/21.Am21,Kimz2+1 Am2+..,Km:Am) ①在B树的中查找关键字K,若找到,表明关键字 已存在,返回:否则,K的查找操作失败于某个叶子 并将中间关键字Km2插入到p的父结点中,以分裂 结点,转②: 后的两个结点作为中间关键字Km2的两个子结点。 ②将K插入到该叶子结点中,插入时,若: 当将中间关键字Km2插入到p的父结点后,父结点 也可能不满足m阶B树的要求(分枝数大于),则必须 ◆叶子结点的关键字数<m-1:直接插入: 对父结点进行“分裂”,一直进行下去,直到没有父结点 ◆叶子结点的关键字数m1:将结点“分裂”。 或分裂后的父结点满足阶B树的要求。 2
2 7 ◆ 若key[i]ptr[i]; ◆ 若K>key[keynum]:T=T->ptr[keynum]; 转①,直到T是叶子结点且未找到相等的关键字,则 查找失败。 ⑵ 算法实现 int BT_search(BTNode *T, KeyType K, BTNode *p) /* 在B_树中查找关键字K, 查找成功返回在结点中的位置 */ /* 及结点指针p; 否则返回0及最后一个结点指针 */ { BTNode *q ; int n ; p=q=T ; 8 while (q!=NULL) { p=q ; q->key[0]=K ; /* 设置查找哨兵 */ for (n=q->keynum ; Kkey[n] ; n--) if (n>0&&EQ(q->key[n], K) ) return n ; q=q->ptr[n] ; } return 0 ; } ⑶ 算法分析 在B_树上的查找有两中基本操作: ◆ 在B_树上查找结点(查找算法中没有体现); 9 ◆ 在结点中查找关键字:在磁盘上找到指针ptr所指 向的结点后,将结点信息读入内存后再查找。因此, 磁盘上的查找次数(待查找的记录关键字在B_树上的 层次数)是决定B_树查找效率的首要因素。 根据m阶B_树的定义,第一层上至少有1个结点, 第二层上至少有2个结点;除根结点外,所有非终端结 点至少有⎡m/2⎤棵子树,…,第h层上至少有⎡m/2⎤h-2个 结点。在这些结点中:根结点至少包含1个关键字,其 它结点至少包含⎡m/2⎤-1个关键字,设s=⎡m/2⎤,则总的 关键字数目n满足: n≧1+(s-1)∑ 2si-2=1+ i=2 h =2sh-1-1 s-1 sh-1-1 2(s-1) 10 因此有: h≦1+ ㏒s((n+1)/2)=1+㏒⎡m/2⎤((n+1)/2) 即在含有n个关键字的B_树上进行查找时,从根结 点到待查找记录关键字的结点的路径上所涉及的结点数 不超过1+ ㏒⎡m/2⎤((n+1)/2) 。 11 3 B_树的插入 B_树的生成也是从空树起,逐个插入关键字。插 入时不是每插入一个关键字就添加一个叶子结点,而是 首先在最低层的某个叶子结点中添加一个关键字,然后 有可能“分裂”。 ⑴ 插入思想 ① 在B_树的中查找关键字K,若找到,表明关键字 已存在,返回;否则,K的查找操作失败于某个叶子 结点,转 ②; ② 将K插入到该叶子结点中,插入时,若: ◆ 叶子结点的关键字数<m-1:直接插入; ◆ 叶子结点的关键字数=m-1:将结点“分裂” 。 12 ⑵ 结点“分裂”方法 设待“分裂”结点包含信息为: (m,A0,K1,A1,K2,A2,… ,Km,Am),从其 中间位置分为两个结点: (⎡m/2⎤-1,A0,K1,A1,… ,K⎡m/2⎤-1 ,A⎡m/2⎤-1 ) (m-⎡m/2⎤,A⎡m/2⎤,K⎡m/2⎤+1,A⎡m/2⎤+1 ,… ,Km,Am ) 并将中间关键字K⎡m/2⎤插入到p的父结点中,以分裂 后的两个结点作为中间关键字K⎡m/2⎤的两个子结点。 当将中间关键字K⎡m/2⎤插入到p的父结点后,父结点 也可能不满足m阶B_树的要求(分枝数大于m),则必须 对父结点进行“分裂”,一直进行下去,直到没有父结点 或分裂后的父结点满足m阶B_树的要求

当根结点分裂时,因没有父结点,则建立一个新的 f 分裂m 根,B树增高一层。 b h m 例(下页):在二个3阶B树(23树)上插入结点的 a)一操2-3 b)插入d后 [⊙浙入p后并进行分裂 过程。 f m 分裂 f h m ()算法实现 bd b d p 要实现插入,首先必须考虑结点的分裂。设待分 d描入后 e侧)描入g后并进行分要 裂的结点是p,分裂时先开辟一个新结点,依此将结点p 中后半部分的关键字和指针移到新开辟的结点中。分裂 fh m 分裂 之后,而需要插入到父结点中的关键字在P的关键字向 量的p->keynum+1位置上。 b d b d g 0缝续进行分裂 在B中进行入的过程 BTNode *split(BTNode*p) void insert BTree(BTNode 'T,KeyType K) *结点p中包含个关键字,从中分裂出一个新的结点*/ 严在B树T中插入关键字K, BTNode*q;int k,mid,j; BTNode *q,*s1=NULL,*s2=NULL int n: q=(BTNode *)malloc(sizeof(BTNode)): if(BT search(T,K,p)】 严树中不存在关键字K mid=(m+1)/2;q->ptr[o]=p->ptr[mid] while (pl=NULL) for (j=1,k=mid+1;kkey]=p->key[k] {p->key0=K;”设置晴兵y q->ptr[j++]=p->ptr[k] for (n=p->keynum Kkey[n]n--) }广将p的后半部分移到新结点q中】 p->key[n+1]=p->key[n] q->keynum=m-mid p->keynum=mid-1 p->ptr[n+1]=p->ptr[n] return(q); }产后移关键字和指针*7 p->key[n]=K;p->ptr[n-1]=s1 p->ptrn+1]=s2;P置关键字K的左右指针7 利用m阶B树的插入操作,可从空树起,将一组 if (++(p->keynum ))key[p->keynum+1]; 4B树的删除 p=p->parent;P取出父结点I 在B树上删除一个关键字K,首先找到关键字所在 } 的结点N,然后在N中进行关键字K的删除操作。 } 若N不是叶子结点,设K是N中的第个关键字,则 f(p==NU儿L)严需要产生新的根结点y 将指针A,所指子树中的最大关键字(或最小关键字)K放 p=(BTNode*)malloc(sizeof(BTNode)): 在(K的位置,然后删除K,而K一定在叶子结点上。如 p->keynum=1;p->key[1]=K 图,删除关键字h,用关键字g代替h的位置,然后再从 p->ptr[0]=s1:p->ptr[1]=s2: 叶子结点中删除关键字g· 3
3 13 当根结点分裂时,因没有父结点,则建立一个新的 根,B_树增高一层。 例(下页):在一个3阶B_树(2-3树)上插入结点的 过程。 ⑶ 算法实现 要实现插入,首先必须考虑结点的分裂。设待分 裂的结点是p,分裂时先开辟一个新结点,依此将结点p 中后半部分的关键字和指针移到新开辟的结点中。分裂 之后,而需要插入到父结点中的关键字在p的关键字向 量的p->keynum+1位置上。 14 f b h m (a) 一棵2-3树 f b d h m (b) 插入d后 f b d h m p 分裂 (c) 插入p后并进行分裂 h f m b d p h l f m b d p (d) 插入l后 分裂 g h l f m b d p (e) 插入g后并进行分裂 l f h m b d p p 分裂 在B_树中进行插入的过程 l f h m b d g p b d g l p h f m (f) 继续进行分裂 15 BTNode *split(BTNode *p) /* 结点p中包含m个关键字,从中分裂出一个新的结点 */ { BTNode *q ; int k, mid, j ; q=(BTNode *)malloc(sizeof( BTNode)) ; mid=(m+1)/2 ; q->ptr[0]=p->ptr[mid] ; for (j=1,k=mid+1; kkey[j]=p->key[k] ; q->ptr[j++]=p->ptr[k] ; } /* 将p的后半部分移到新结点q中 */ q->keynum=m-mid ; p->keynum=mid-1 ; return(q) ; } 16 void insert_BTree(BTNode *T, KeyType K) /* 在B_树T中插入关键字K,*/ { BTNode *q, *s1=NULL, *s2=NULL ; int n ; if (!BT_search(T, K, p)) /* 树中不存在关键字K */ { while (p!=NULL) { p->key[0]=K ; /* 设置哨兵 */ for (n=p->keynum ; Kkey[n] ; n--) { p->key[n+1]=p->key[n] ; p->ptr[n+1]=p->ptr[n] ; } /* 后移关键字和指针 */ p->key[n]=K ; p->ptr[n-1]=s1 ; 17 p->ptr[n+1]=s2 ; /* 置关键字K的左右指针 */ if (++(p->keynum ))key[p->keynum+1] ; p=p->parent ; /* 取出父结点*/ } } if (p==NULL) /* 需要产生新的根结点 */ { p=(BTNode*)malloc(sizeof( BTNode)) ; p->keynum=1 ; p->key[1]=K ; p->ptr[0]=s1 ; p->ptr[1] =s2 ; } } } 18 4 B_树的删除 在B_树上删除一个关键字K ,首先找到关键字所在 的结点N,然后在N中进行关键字K的删除操作。 若N不是叶子结点,设K是N中的第i个关键字,则 将指针Ai-1所指子树中的最大关键字(或最小关键字)K’放 在(K)的位置,然后删除K’,而K’一定在叶子结点上。如 图,删除关键字h,用关键字g代替h的位置,然后再从 叶子结点中删除关键字g。 利用m阶B_树的插入操作,可从空树起,将一组 关键字依次插入到m阶B_树中,从而生成一个m阶B_ 树

(h 从叶子结点中删除一个关键字的情况是 除 除 (I)若结点N中的关键字个数fm21:在结点中直 接删除关键字K,如图(b)∽©所示。 (2)若结点N中的关键字个数「m21:若结点N的 a 左(右)兄弟结点中的关键字个数fm2L1,则将结点 N的左(或右)兄弟结点中的最大(或最小)关键字上移 除 除 到其父结点中,而父结点中大于(或小于)且紧靠上移 m m b 关键字的关键字下移到结点N,如图(a)。 (3)若结点N和其兄弟结点中的关键字数-21: P e P (d) 删除结点N中的关键字,再将结点N中的关键字、指 回 针与其兄弟结点以及分割二者的父结点中的某个关 在B树中进行侧除的过程 键字K,合并为一个结点,若因此使父结点中的关 键字个数「m21则依世类推.如图(d 算法实现 if(b->keynum>(m-1)/2) 严左邻兄弟有多余关键字) 在B树上删除一个关键字的操作,针对上述的(2) 和(3的情况,相应的算法如下: for (k=p->keynum;k>=0;K--) {p->keyk+1片p->key[k int BTNode MoveKey(BTNode*p) p->ptr[k+1]=p->ptr[k]: P将命的左(或右)兄弟结点中的最大(成最小)关键字上移 】严将印中关键字和指针后移 广到其父结点中,父结点中的关键字下移到中/ p->key[1]=f->key[j]: {BTNode*b,*f=p->parent;产f指向p的父结点7 f->key[j]=b->key[keynum]; int k.j; 严f仲关键字下移到卵,b中最大关键字上移到y for0片0:f>pt=p:j+)产在仲找p的位置7 p->ptr[0]=b->ptr[keynum]; f>0)IP若D有左邻兄第结点7 p->keynum++: 22 {b=f->ptf-11:Pb指向p的左邻兄弟7 b->keynum-; return(1) b->key[k]=b->key[k+1]: b->ptr[k]=b->ptr[k+1]; fGkeynum严若p有右邻兄弟结点y 】产将6中关键字和指针前移 {b=f->pt+1]:Pb指向p的右邻兄弟v p->keynum++; if (b->keynum>(m-1)/2) b->keynum--; 严右邻兄弟有多余关键字1 return(1); p->key[p->keynum]=f->key[j+1]; f->key1]片b-keyM1]: p->ptr[p->keynum]=b->ptr[0]: return(0); P仲关键字下移到P,b中最小关键字上移到fV 】左右兄弟中无多余关键字移动失败习 for (k=0;kkeynum;k++) 4
4 19 在B_树中进行删除的过程 删除q b d e g l m q h f p b d e g l p h f m 删除h (a) 删除e b d e l p g f m b e l p g f m 删除d l p g m b f (b) (c) (d) 20 从叶子结点中删除一个关键字的情况是: ⑴ 若结点N中的关键字个数>⎡m/2⎤-1:在结点中直 接删除关键字K,如图 (b)∽©所示。 ⑵ 若结点N中的关键字个数=⎡m/2⎤-1:若结点N的 左(右)兄弟结点中的关键字个数>⎡m/2⎤-1,则将结点 N的左(或右)兄弟结点中的最大(或最小)关键字上移 到其父结点中,而父结点中大于(或小于)且紧靠上移 关键字的关键字下移到结点N,如图 (a)。 ⑶ 若结点N和其兄弟结点中的关键字数=⎡m/2⎤-1: 删除结点N中的关键字,再将结点N中的关键字、指 针与其兄弟结点以及分割二者的父结点中的某个关 键字Ki ,合并为一个结点,若因此使父结点中的关 键字个数parent ; /* f指向p的父结点 */ int k, j ; for (j=0; f->ptr[j]!=p; j++) /* 在f中找p的位置 */ if (j>0) /* 若p有左邻兄弟结点 */ { b=f->ptr[j-1] ; /* b指向p的左邻兄弟 */ 22 if (b->keynum>(m-1)/2) /* 左邻兄弟有多余关键字 */ { for (k=p->keynum; k>=0; k--) { p->key[k+1]=p->key[k]; p->ptr[k+1]=p->ptr[k]; } /* 将p中关键字和指针后移 */ p->key[1]=f->key[j]; f->key[j]=b->key[keynum] ; /* f中关键字下移到p, b中最大关键字上移到f */ p->ptr[0]= b->ptr[keynum] ; p->keynum++ ; b->keynum-- ; 23 return(1) ; } if (jkeynum) /* 若p有右邻兄弟结点 */ { b=f->ptr[j+1] ; /* b指向p的右邻兄弟 */ if (b->keynum>(m-1)/2) /* 右邻兄弟有多余关键字 */ { p->key[p->keynum]=f->key[j+1] ; f->key[j+1]=b->key[1]; p->ptr[p->keynum]=b->ptr[0]; /* f中关键字下移到p, b中最小关键字上移到f */ for (k=0; kkeynum; k++) 24 { b->key[k]=b->key[k+1]; b->ptr[k]=b->ptr[k+1]; } /* 将b中关键字和指针前移 */ p->keynum++ ; b->keynum-- ; return(1) ; } } return(0); } /* 左右兄弟中无多余关键字,移动失败 */ }

BTNode *MergeNode(BTNode *p) free(p) ”将命与其左(右)邻兄弟合并返回合并后的结点指针7 for (k=j+1;kkeynum k++) BTNode *b,f=p->parent; f->key[k-1]=f->key[k] int j.k; f->ptr[k-1]=f->ptrik] for0=0:f>pt归p:jt+)严在f仲我出p的位道7 }P将仲第个关键字和指针前移制 f0>0)b=千>pt邮-小Pb指向p的左邻兄弟y f->keynum-: else{b=p;p=p->ptr+小}Pp指向p的右邻I return(他)i b->key[++b->keynum]=f->key[j] b->ptr[p->keynum]=p->ptr[0] for (k=1;kkeynum k++) b->key[++b->keynum]=p->key[k] b->ptr[b->keynum]=p->ptr[k] ”将印中关键字和指针移到b中) void DeleteBTNode(BTNode*T,KeyType K) for (n=j+1:nkeynum;n++) BTNode 'p,*S: p->key[n-1]=p->key[n] intj.n 产从p中刷除第m个关键字) 片BT_search(T,Kp):r在T中查找K的结点7 p->keynum-: if (j==0)return(T) while (p->keynumparent) ifp>pt切 if(IMoveKey(p))p=MergeNode(p): {S=p->ptrli-11 p=p->parent: while (S->ptr[S->keynum]) S=S->ptr[S->keynum]; 】”若P中关键字树目不够按2处理7 if (p==T&&T->keynum==0) 严在子树中找包含最大关键字的结点) p->key[]=S->key[S->keynum] T=T->ptr[o]:free(p); p=S;j=S->keynum 5 B树 (3)所有的非叶子结点可以看成是索引的部分,结点 中只含有其子树的根结点中的最大(或最小)关键字。 在实际的文件系统中,基本上不使用B树,而是使 如图所示是一棵3阶B+树。 用B树的一种变体,称为m阶B树。它与B树的主要 不同是叶子结点中存储记录。在B树中,所有的非叶子 由于B树的叶子结点和非叶子结点结构上的显著区 结点可以看成是索引,而其中的关键字是作为分界关 别,因此需要一个标志域加以区分,结点结构定义如 键字”,用来界定某一关键字的记录所在的子树。一棵 下: 阶B树与m阶B树的主要差异是: 3596 ()若一个结点有n棵子树,则必含有n个关键字: 1735 587696 (②)所有叶子结点中包含了全部记录的关键字信息以 1923354149586376 798496 及这些关键字记录的指针,而且叶子结点按关键字 的大小从小到大顺序链接 一3阶B树■ 5
5 25 BTNode *MergeNode(BTNode *p) /* 将p与其左(右)邻兄弟合并,返回合并后的结点指针 */ { BTNode *b, f=p->parent ; int j, k ; for (j=0; f->ptr[j]!=p; j++) /* 在f中找出p的位置 */ if (j>0) b=f->ptr[j-1]; /* b指向p的左邻兄弟 */ else { b=p; p=p->ptr[j+1]; } /* p指向p的右邻 */ b->key[++b->keynum]=f->key[j] ; b->ptr[p->keynum]=p->ptr[0] ; for (k=1; kkeynum ; k++) { b->key[++b->keynum]=p->key[k] ; b->ptr[b->keynum]=p->ptr[k] ; } /* 将p中关键字和指针移到b中 */ 26 free(p); for (k=j+1; kkeynum ; k++) { f->key[k-1]=f->key[k] ; f->ptr[k-1]=f->ptr[k] ; } /* 将f中第j个关键字和指针前移 */ f->keynum-- ; return(b) ; } 27 void DeleteBTNode(BTNode *T, KeyType K) { BTNode *p, *S ; int j,n ; j=BT_search(T, K, p) ; /* 在T中查找K的结点 */ if (j==0) return(T) ; if (p->ptr[j-1]) { S=p->ptr[j-1] ; while (S->ptr[S->keynum]) S=S->ptr[S->keynum] ; /* 在子树中找包含最大关键字的结点 */ p->key[j]=S->key[S ->keynum] ; p=S ; j=S->keynum ; } 28 for (n=j+1; nkeynum; n++) p->key[n-1]=p->key[n] ; /* 从p中删除第m个关键字 */ p->keynum-- ; while (p->keynumparent) { if (!MoveKey(p) ) p=MergeNode(p); p=p->parent ; } /* 若p中关键字树目不够,按⑵处理 */ if (p==T&&T->keynum==0) { T=T->ptr[0] ; free(p) ; } } 29 5 B+树 在实际的文件系统中,基本上不使用B_树,而是使 用B_树的一种变体,称为m阶B+树。 它与B_树的主要 不同是叶子结点中存储记录。在B+树中,所有的非叶子 结点可以看成是索引,而其中的关键字是作为“分界关 键字”,用来界定某一关键字的记录所在的子树。一棵m 阶B+树与m阶B_树的主要差异是: ⑴ 若一个结点有n棵子树,则必含有n个关键字; ⑵ 所有叶子结点中包含了全部记录的关键字信息以 及这些关键字记录的指针,而且叶子结点按关键字 的大小从小到大顺序链接; 30 ⑶ 所有的非叶子结点可以看成是索引的部分,结点 中只含有其子树的根结点中的最大(或最小)关键字。 如图所示是一棵3阶B+树。 由于B+树的叶子结点和非叶子结点结构上的显著区 别,因此需要一个标志域加以区分,结点结构定义如 下: 一棵3阶B+树 35 96 17 35 58 76 96 5 12 17 19 23 35 41 49 58 63 76 79 84 96

typedef enum(branch,left}NodeType; 与B树相比,对B树不仅可以从根结点开始按关 typedef struct BPNode 键字随机查找,而且可以从最小关键字起,按叶子结点 的链接顺序进行顺序查找。在B树上进行随机查找、插 {NodeTag tag;r结点标志y 入、 删除的过程基本上和B树类似。 nt keynum;P结点中关键字的个数司 在B+树上进行随机查找时,若非叶子结点的关键字 struct BTNode *parent:指向父结点的指针 等于给定的K值,并不终止,而是继续向下直到叶子结 点(只有叶子结点才存储记录),即无论查找成功与否, KeyType key[M+1];r组关键字向量key[O]未用 都走了一条从根结点到叶子结点的路径。 B树的插入仅仅在叶子结点上进行。当叶子结点中 union pointer 的关键字个数大于时,“分裂”为两个结点,两个结点 (struct BTNode 'ptr[M+1j:P子树指针向量 中所含有的关键字个数分别是L(m+1)2和(m+1)/21, RecType*recptr[M+1);"recptr[o]味用t 且将这两个结点中的最大关键字提升到父结点中,用来 替代原结点在父结点中所对应的关键字。提升后父结点 ptrType:P用联合体定义子树指针和记录指针 又可能会分裂,依次类推。 BPNode §9.4散列技术 §9.4.1散列表的概念 鲁压缩映象: 上述查找均是基于k©y的比较,由判定树可证明,在 平均和最坏情况下所需的此较次数的下界是: ◆例于:设影德出粗店 Ign+0(1) 总片数:10,000张 要突破此界,就不能只依懒于比较来进行, 僧还:500人次海天 记录,(电话号码,姓名,住址,),Ky为7位电话号网 直核寻址:须保需1000万个记录 59.4.1散列表的禄念 但奖际只曼大于500即可,量多1万个记录 ●直接寻址:当结点的k©y和存储位置间建立某种关系时, 令一搬信淀 无须比较即可找到结点的存储位置。 金集:可能发生的关量字填合,即关整字的取值氯合 例如,若500个结点的keys取值为1~500间互不相 实际发生第K:实际常要存销的关轴字集合 同的整数,则keys可作为下标,将其存储到T[1.500]之 中,寻址时间为0(1)。 :KN<U,当豪T的规横取U浪费空间,有时塔至无法实现 :T的视模一般取O(K),但压输存雠后失去了直核寻址的功能 3 S9.41散列表的概念 S9.4.1散列表的概念 ■数列(hash)西数h 不下你出来来丝之周立一个对应关系,养金集快前到印m南 。敢列(hash)西败h ◆神突碰撞:若k≠k,有h(k)=h(k) h:U-{0,1,,m-1) hash 存储地址 ◆同义词:发生冲突的两个关键字互为同义词(相对于) 寸k,eU,hk)∈{0,1,m-1】 集合 集合 女能完全避免冲突吗? ◆数列液:T 须满足:①U川≤m②选择合适的hah函数 ◆数列地址(散列值):散列西数值k T0.m- g散列(hashing), 0 否则只能设计好的使冲突尽可能少 ◆解决冲突:须确定处理冲突的方法 h(k2) ◆装填因子:冲突的频繁程度除了与的好坏相关,还与表的 填满程度相关 h(k,尸h(k a=n/m.0≤a≤1 m-1 35 6
6 31 typedef enum{branch, left} NodeType ; typedef struct BPNode { NodeTag tag ; /* 结点标志 */ int keynum ; /* 结点中关键字的个数 */ struct BTNode *parent ; /* 指向父结点的指针 */ KeyType key[M+1] ; /* 组关键字向量,key[0]未用 */ union pointer { struct BTNode *ptr[M+1] ; /* 子树指针向量 */ RecType *recptr[M+1] ; /* recptr[0]未用 */ }ptrType ; /* 用联合体定义子树指针和记录指针 */ }BPNode ; 32 与B_树相比,对B+树不仅可以从根结点开始按关 键字随机查找,而且可以从最小关键字起,按叶子结点 的链接顺序进行顺序查找。在B+树上进行随机查找、插 入、删除的过程基本上和B_树类似。 在B+树上进行随机查找时,若非叶子结点的关键字 等于给定的K值,并不终止,而是继续向下直到叶子结 点(只有叶子结点才存储记录) , 即无论查找成功与否, 都走了一条从根结点到叶子结点的路径。 B+树的插入仅仅在叶子结点上进行。当叶子结点中 的关键字个数大于m时,“分裂”为两个结点,两个结点 中所含有的关键字个数分别是⎣(m+1)/2⎦和⎡ (m+1)/2⎤ , 且将这两个结点中的最大关键字提升到父结点中,用来 替代原结点在父结点中所对应的关键字。提升后父结点 又可能会分裂,依次类推。 33 § 9.4 散列技术 上述查找均是基于key的比较,由判定树可证明,在 平均和最坏情况下所需的比较次数的下界是: lgn+O(1) 要突破此界,就不能只依赖于比较来进行。 § 9.4.1 散列表的概念 直接寻址:当结点的key和存储位置间建立某种关系时, 无须比较即可找到结点的存储位置。 例如,若500个结点的keys取值为1~500间互不相 同的整数,则keys可作为下标,将其存储到T[1..500]之 中,寻址时间为O (1)。 34 § 9.4.1 散列表的概念 压缩映象: 例子:设影像出租店 总片数:10,000张 借还:500人次/每天 记录:(电话号码,姓名,住址,…), Key为7位电话号码 直接寻址:须保留1000万个记录 但实际只要大于500即可,最多1万个记录 一般情况 全集U:可能发生的关键字集合,即关键字的取值集合 实际发生集K:实际需要存储的关键字集合 ∵ |K| << |U|,当表T的规模取|U|浪费空间,有时甚至无法实现 ∴ T的规模一般取O(K), 但压缩存储后失去了直接寻址的功能 35 § 9.4.1 散列表的概念 散列(hash)函数h 在keys和表地址之间建立一个对应关系h,将全集U映射到T[0..m-1]的 下标集上: h:U→{ 0, 1, … , m-1 } ∀ki ∈U,h(ki ) ∈ { 0,1,…,m-1 } 散列表: T 散列地址(散列值):散列函数值h(ki ) 散列(hashing): 关键字 集合 存储地址 集合 hash U. . . K k1 . . . . k2 . . . k3. h(k2) h(k1)=h(k3) 0 m-1 T[0..m-1] 36 § 9.4.1 散列表的概念 散列(hash)函数h 冲突(碰撞): 若ki ≠kj ,有h(ki ) = h(kj ) 同义词:发生冲突的两个关键字互为同义词(相对于h) 能完全避免冲突吗? 须满足:① |U|≤m ② 选择合适的hash函数 否则只能设计好的h使冲突尽可能少 解决冲突: 须确定处理冲突的方法 装填因子:冲突的频繁程度除了与h的好坏相关,还与表的 填满程度相关 α=n/m, 0≤ α ≤ 1

§9.4.2散列函数的构造方法 §9.4.2散列函数的构造方法 ■原则:简单、均匀 2、除余法 用表长除以关输字,取其余数作为散列地址 简单一一计算快速,均匀一一冲突最小化 h(k=k%p:p≤m,有时取p=m ·假定:关笔宇定义在自然数集合上,否则将其转换到 p最好取素数,或取不包含小于20的质因数的合数 自然数巢合上 优点:录简单,无需定义为西取,直接写到程序里使用 1、平方取中法 3、随机数法 先通过平方扩大相近数的差别,然后取中间的若干位作为散 h(k)=random(k ) 列地址。因为中间位和数的每一位相关,故产生的地址较 伪随机函数须保亚函数值在0一m一1之间 为均匀。 ■选取哈希函数,考虑的因素 int Hash(int k ) 产计前哈希函数所需时间 k=k;k仁100;法掉末尾两位数 关字长度 return k%1000;取中间3位,T的地址为0-999 一哈稀表长度(哈格地址范围司 。关键字分布销限 3 记的童找频 §9.43处理冲突的方法 §9.43处理冲突的方法 1、开放地址法(闭散列) ■开放地址法分类:按照形成探测序列的方法不同,可将其分为3 程特袋鞋种影成 类:线性探测、二次探测、双重散列法 个单元查我,直到找到给定的k©y, (1)线性探测法 或碰到1个并放地址(空草元)为止 ◆插入时,探测到开地址可将新结点插入其中 ■基本周想:将T0.m-1们看作一循环向量,令d=i,即 ◆查找时,探测到开地址衰示查找失败 h=(h(k)+iD%m0≤i≤m-1 ◆开地址表示:与应用相关,如ky为串时,用空串表示开地 若令d=h(k),则量长的探测序列为: 址 d,d+1,.,m-1,0,1,,d-1 ■一般形式 探测过程线止于 h=(h(k)+d)%m 1≤i≤m一1(9.1) ◆绿测到空单元:查找时失败,浙入时写入 探测序列:h(k),h,h2,,hm ◆绿测到含有k的单元:查找时成功,滑入时失败 开地址法要求:α<1,实用中0.5≤a≤0.9 ◆探测到T-们但未出现上述2种情况:查找、撕入均失败 §9.4.3处理冲突的方法 §9.4.3处理冲突的方法 ■例1:已知一组keys为(26,36,41,38,44,15,68,12,06,51),用 非同义澜冲突:上例中,h152,h(63)-3,15和68不是同义调,但 除余法和线性探测法构造散列衰 是15和41达两个同义词处理过程中,15先占用了T3],异数播入68时 发生了非同义词的冲突。 解::a<1,n=10,不妨取m=13,此时a0.77 糜集(维取),一般地,用战性探测法解块冲突时,当豪中,+1 h(k=k%13keys:(26,36,44,38,44.15,68,12,06,51) 同一地址:计k+,这种不同地址的铺点夺间后应衡特卖 的位上电有结点时, 到地址为礼 对应的散列地址:(0,10,2,125,2,3,12,6,12) 称为雅集。 聚集增加了探测序列的长度,使查找时间增加。应端联式地散列。 0123456789101112 0123456789101112 网2614 3638 1264143638 26241156840651☐☐36☐38 261241584406513638 探测次13122119 探测次数13122119 1 1 7
7 37 § 9.4.2 散列函数的构造方法 原则:简单、均匀 简单--计算快速,均匀--冲突最小化 假定:关键字定义在自然数集合上,否则将其转换到 自然数集合上 1、平方取中法 先通过平方扩大相近数的差别,然后取中间的若干位作为散 列地址。因为中间位和乘数的每一位相关,故产生的地址较 为均匀。 int Hash( int k ) { k *=k; k /=100; //去掉末尾两位数 return k%1000;//取中间3位,T的地址为0~999 } 38 § 9.4.2 散列函数的构造方法 2、除余法 用表长除以关键字,取其余数作为散列地址 h(k)= k%p; p≤m,有时取p=m p最好取素数,或取不包含小于20的质因数的合数 优点:最简单,无需定义为函数,直接写到程序里使用 3、随机数法 h(k)=random( k ); 伪随机函数须保证函数值在0~m-1之间 选取哈希函数,考虑的因素 ¾ 计算哈希函数所需时间 ¾ 关键字长度 ¾ 哈希表长度(哈希地址范围) ¾ 关键字分布情况 ¾ 记录的查找频率 39 § 9.4.3 处理冲突的方法 1、开放地址法(闭散列) 基本思想:当发生冲突时,使用某种探测技术在散列表中形成 一个探测序列,沿此序列逐个单元查找,直到找到给定的key, 或碰到1个开放地址(空单元)为止 插入时,探测到开地址可将新结点插入其中 查找时,探测到开地址表示查找失败 开地址表示:与应用相关,如key为串时,用空串表示开地 址 一般形式 hi =(h(k)+di )%m 1 ≤i ≤ m-1 (9.1) 探测序列:h(k), h1, h2 , …, hm-1 开地址法要求:α<1, 实用中 0.5≤ α ≤ 0.9 40 § 9.4.3 处理冲突的方法 开放地址法分类:按照形成探测序列的方法不同,可将其分为3 类:线性探测、二次探测、双重散列法 (1)线性探测法 基本思想:将T[0..m-1]看作一循环向量,令di =i,即 hi =(h(k)+i)%m 0 ≤i ≤ m-1 若令d=h(k),则最长的探测序列为: d,d+1,…,m-1,0,1,…,d-1 探测过程终止于 探测到空单元:查找时失败,插入时写入 探测到含有k的单元:查找时成功,插入时失败 探测到T[d-1] 但未出现上述2种情况:查找、插入均失败 41 § 9.4.3 处理冲突的方法 例1:已知一组keys为(26,36,41,38,44,15,68,12,06,51), 用 除余法和线性探测法构造散列表 解:∵ α<1,n=10,不妨取m=13,此时α≈0.77 h( k )= k%13 keys:(26,36,41,38,44,15,68,12,06,51) 对应的散列地址:( 0,10, 2, 12, 5, 2, 3, 12, 6, 12) 0 1 2 3 4 5 6 7 8 9 10 11 12 26 41 44 36 38 26 12 41 15 68 44 06 51 36 38 1 3 1 2 2 1 1 9 1 1 T[0..12] 探测次数 42 § 9.4.3 处理冲突的方法 非同义词冲突:上例中,h(15)=2,h(68)=3,15和68不是同义词,但 是15和41这两个同义词处理过程中,15先占用了T[3],导致插入68时 发生了非同义词的冲突。 聚集(堆积):一般地,用线性探测法解决冲突时,当表中i,i+1,…,i+k 的位置上已有结点时,一个散列地址为i,i+1,…,i+k,i+k+1的结点都将争 夺同一地址:i+k+1。这种不同地址的结点争夺同一后继地址的现象 称为聚集。 聚集增加了探测序列的长度,使查找时间增加。应跳跃式地散列。 0 1 2 3 4 5 6 7 8 9 10 11 12 26 41 44 36 38 26 12 41 15 68 44 06 51 36 38 1 3 1 2 2 1 1 9 1 1 T[0..12] 探测次数

§9.4.3处理冲突的方法 ⑧9.4.3处理冲突的方法 2、拉链法(开做列) (2)二次探测法; 鞋卦号意麻产足受男监竿实辣瓷服的清赞赞造煮笑 探测序列为(增量序列为d,=P力 初征为空。 例2:keys和hash函数同前例 h=(h(k)+ii)%m 0≤i≤m-1 0 26勺 缺点:不易探测到整个空间 A 41子5 (3)双量散列法: 68 是开地址法中量好的方法之一,探测序列为 44 h;=(h(k)+ih(k))%m 0≤i≤m一1 06 即:d=ih,k) 9A 特点:使用了两个散列函数,一般须使h,(k)的值与m互素 36 子8□2□闪 比较次数: 2 3 §9.4.3处理冲突的方法 §9.4.4散列表上的运算 特点 仅给出开放定址法处理冲突时的相关运算 无堆积现象、非同义词不会冲突、ASL较短 存储结构 ◆无法预先确定表长度时,可选此方法 define NIL-1/空结点标记 ◆除操作男于实现,开地址方法只能微除标记 #define m997l表长,依嫩应用和c typedef struct{ ◆允许a>1.当n较大时,节省空间 KeyType key: 。 )NodeType,HashTable[m]: 1、查找运算 和建表类似,使用的函数和处理冲突的方法应与建表一致 开地址可统一处理 S9.4.4散列表上的运算 S9.4.4散列表上的运算 int Hash(KeyType K,int i) 2、插入和建表 return(h(K+Increment(i))%m;/Increment相当于d ■擂入:先查找,找到开地址成功,否则(表满、K存在)失败 void Hashinsert(HashTable T,NodeType new ) Int HashSearch(HashTable T,KeyType K,int *pos){ int pos,sign; int=0;深测次数计敷圈 sign=HashSearch(T,new.key,&pos ) do(pos=Hash(K,i)方I求探测地址h f(sign)标记为0,是开地址 T[pos]=new;:精入城动 f(Tt'posJ.key==K)return1;成功 else if(Tpos].key=NIL)return0;I失敷 if(sign>0)printf("duplicate key"”;l量复,捕入失敷 )while(t+iKm;最多探测m次 else Error('overflow";衰清,播入失戴 return-1;可能是衰清,失败 建表:将表中kys清空,然后依次调用插入算法插入结点B 8
8 43 § 9.4.3 处理冲突的方法 (2)二次探测法: 探测序列为( 增量序列为di =i2 ): hi =(h(k)+i*i)%m 0 ≤i ≤ m-1 缺点:不易探测到整个空间 (3)双重散列法: 是开地址法中最好的方法之一,探测序列为 hi =(h(k)+i* h1(k) )%m 0 ≤i ≤ m-1 即: di =i* h1(k) 特点:使用了两个散列函数,一般须使h1(k)的值与m互素 44 § 9.4.3 处理冲突的方法 2、拉链法(开散列) 基本思想:将所有keys为同义词的结点连接在同一个单链表中,若散列地 址空间为0~m-1,则将表定义为m个头指针组成的指针数组T[0..m-1],其 初值为空。 例2:keys和hash函数同前例 0 1 2 3 4 5 6 7 8 9 10 11 12 44 ^ 41 15 26 68 06 36 38 12 ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ 51 比较次数: 1 2 3 45 § 9.4.3 处理冲突的方法 特点 无堆积现象、非同义词不会冲突、ASL较短 无法预先确定表长度时,可选此方法 删除操作易于实现,开地址方法只能做删除标记 允许α>1,当n较大时,节省空间 46 § 9.4.4 散列表上的运算 仅给出开放定址法处理冲突时的相关运算 存储结构 #define NIL -1 //空结点标记 #define m 997 //表长,依赖应用和α typedef struct { KeyType key; //…. }NodeType, HashTable[m]; 1、查找运算 和建表类似,使用的函数和处理冲突的方法应与建表一致 开地址可统一处理 47 § 9.4.4 散列表上的运算 int Hash( KeyType K, int i){ return ( h(K)+ Increment( i ) )%m; //Increment相当于di } Int HashSearch( HashTable T, KeyType K, int *pos){ int i=0; //探测次数计数器 do { *pos=Hash( K,i ); //求探测地址hi if ( T[*pos].key==K ) return 1; //成功 if ( T[*pos].key==NIL ) return 0; //失败 } while (++i0 ) printf(“duplicate key”) ; //重复,插入失败 else Error(“overflow”); //表满,插入失败 } 建表:将表中keys清空,然后依次调用插入算法插入结点
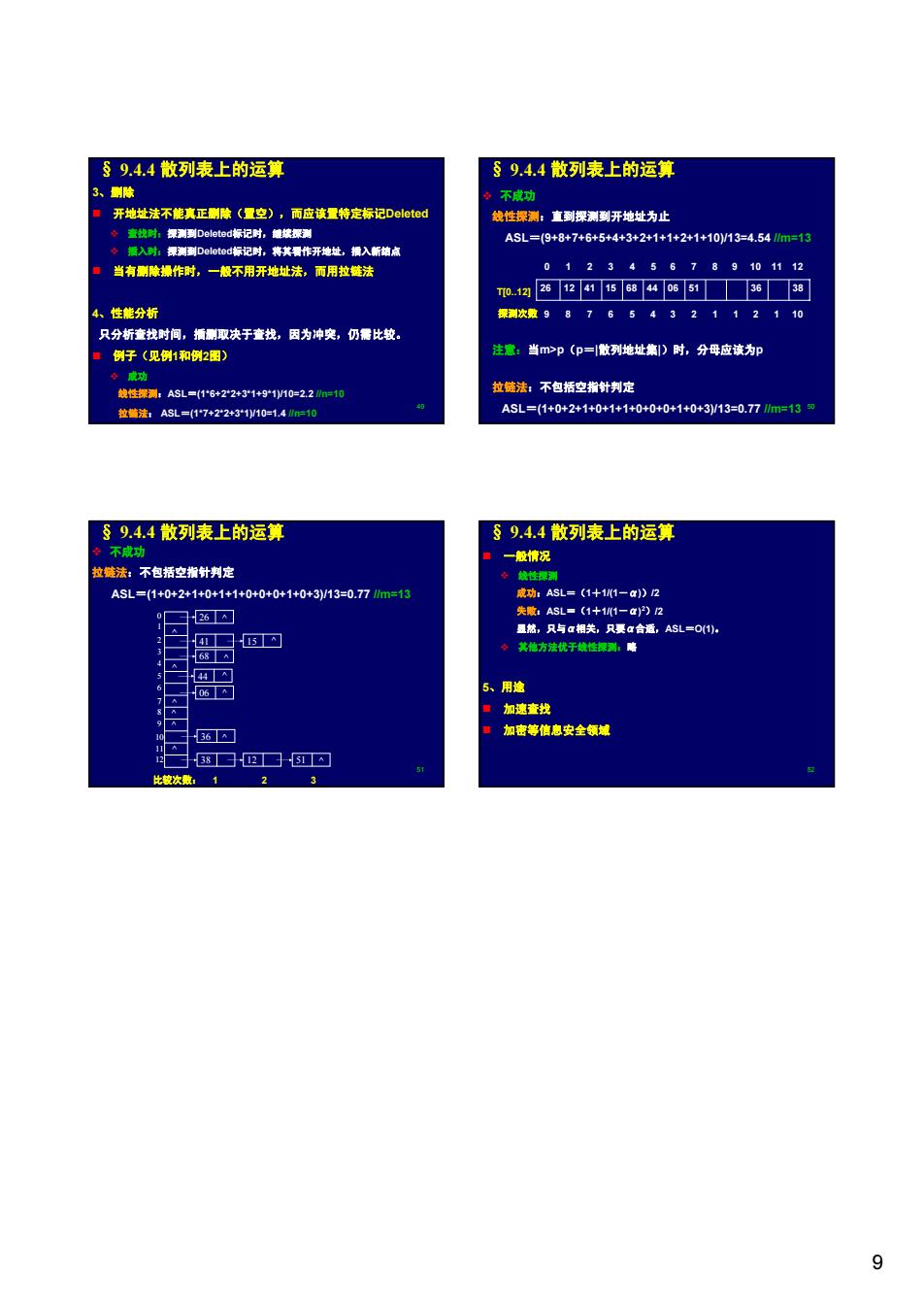
S9.4.4散列表上的运算 §9.4.4散列表上的运算 3、除 ◆不成功 开地址法不能真正除(置空),而应该置特定标记Deleted 线性探测:直到探测到开地址为止 香查找制:银测到Deleted标记时,锁块绿测 ASL=(9+8+7+6+5+4+3+2+1+1+2+1+10/13=4.541m=13 令摘入时:裸测到Deed标记时,将其滑作开地址,捕入新销点 当有除操作时,一般不用开地址法,而用拉链法 0123456789101112 T0.1261241156840651■☐3638 4、性能分析 探测次数98765432112110 只分析查找时间,插取决于查找,因为冲突,仍需比较。 ■例子(见例1和例2图) 注意:当m>p(p=散列地址集)时,分母应该为p 令成功 线性探:ASL=(16+22+31+91)/10=2.2n=10 拉链法:不包括空指针判定 拉藏法:ASL=(17+22+3*1)y10=1.4ln=0 ASL=(1+0+2+1+0+1+1+0+0+0+1+0+3/13=0.771m130 §9.4.4散列表上的运算 §9.4.4散列表上的运算 。不成功 鲁一般情况 拉继法:不包括空指针判定 令就性探闲 ASL=(1+0+2+1+0+1+1+0+0+0+1+0+3)/13=0.77m=13 成功:ASL=(1+1(1-a)2 26A 失意:ASL=(1+1(1-a)2)2 盟然,只与a相关,只要a合适,ASL=O(1)。 4 5冈 ◆其他方法优于线性探,略 68A A 44 06 5、用途 ”加速查找 36 加密等信息安全领城 A 12 3831251 比较次数:1 2 3 9
9 49 § 9.4.4 散列表上的运算 3、删除 开地址法不能真正删除(置空),而应该置特定标记Deleted 查找时:探测到Deleted标记时,继续探测 插入时:探测到Deleted标记时,将其看作开地址,插入新结点 当有删除操作时,一般不用开地址法,而用拉链法 4、性能分析 只分析查找时间,插删取决于查找,因为冲突,仍需比较。 例子(见例1和例2图) 成功 线性探测:ASL=(1*6+2*2+3*1+9*1)/10=2.2 //n=10 拉链法: ASL=(1*7+2*2+3*1)/10=1.4 //n=10 50 § 9.4.4 散列表上的运算 不成功 线性探测:直到探测到开地址为止 ASL=(9+8+7+6+5+4+3+2+1+1+2+1+10)/13=4.54 //m=13 注意:当m>p(p=|散列地址集|)时,分母应该为p 拉链法:不包括空指针判定 ASL=(1+0+2+1+0+1+1+0+0+0+1+0+3)/13=0.77 //m=13 T[0..12] 0 1 2 3 4 5 6 7 8 9 10 11 12 26 12 41 15 68 44 06 51 36 38 探测次数 9 8 7 6 5 4 3 2 1 1 2 1 10 51 § 9.4.4 散列表上的运算 不成功 拉链法:不包括空指针判定 ASL=(1+0+2+1+0+1+1+0+0+0+1+0+3)/13=0.77 //m=13 0 1 2 3 4 5 6 7 8 9 10 11 12 44 ^ 41 15 26 68 06 36 38 12 ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ 51 比较次数: 1 2 3 52 § 9.4.4 散列表上的运算 一般情况 线性探测 成功:ASL=(1+1/(1-α))/2 失败:ASL=(1+1/(1-α)2)/2 显然,只与α相关,只要α合适,ASL=O(1)。 其他方法优于线性探测:略 5、用途 加速查找 加密等信息安全领域