
A1:Crystal Structure (Chapter 1) 7 points a)Draw all the atom positions for BCC and FCC structures in the following unit cell.And mark one of the octahedral gap positions for BCC and FCC respectively in the figure.(3 points) BCC FCC Z b)What is the difference between octahedral gap in FCC and BCC crystal lattice with respect to the space dimensions?(1 point) c)For FCC crystal lattice,write down the mathematic relation between the radius of the octahedral void r,the radius of atom R and the lattice constant a.For BCC crystal lattice,write down TWO different mathematic relations between the radius of octahedral voids r,the radius of atom R and the lattice constant a.(3 points) A2:Texture(Chapter 2) 4points a)What is meant by crystallographic texture?(0.5 points) b)Which is the most important recrystallization component of rolled Aluminium?Give the miller indices of this orientation and plot it in the (200)-polfigure.(2.5 points) c)Give two examples for the technical relevance of crystallographic textures.(1 point)
1 A1: Crystal Structure (Chapter 1) 7 points a) Draw all the atom positions for BCC and FCC structures in the following unit cell. And mark one of the octahedral gap positions for BCC and FCC respectively in the figure. (3 points) BCC FCC b) What is the difference between octahedral gap in FCC and BCC crystal lattice with respect to the space dimensions? (1 point) c) For FCC crystal lattice, write down the mathematic relation between the radius of the octahedral void r, the radius of atom R and the lattice constant a. For BCC crystal lattice, write down TWO different mathematic relations between the radius of octahedral voids r, the radius of atom R and the lattice constant a. (3 points) A2: Texture (Chapter 2) 4points a) What is meant by crystallographic texture? (0.5 points) b) Which is the most important recrystallization component of rolled Aluminium? Give the miller indices of this orientation and plot it in the {200}-polfigure. (2.5 points) c) Give two examples for the technical relevance of crystallographic textures. (1 point)

A3:Low Angle Grain Boundaries(Chapter 3) 8.5 points a)Calculate the number of dislocations per unit length (or rather the length of the dislocation per unit area)in a symmetrical tilt boundary at a misorientation of the neighbouring grains of 1(b=210m).(2.5 points) b)Calculate the energy per area of a low angle tilt boundary as a function of the tilt angle 0.The line energy of a dislocation is: with ro=2b and R=d(d=dislocation spacing).(3 points) c)For which tilt angle (in degree)is the specific grain boundary energy maximal?(2 points) d)During the plastic deformation in a material,dislocations are formed beside other defects,so that after deformation many single dislocations are present.Explain with TWO key points,how the crystal reduces the stored energy of the dislocations.(1 point) A4:Alloying(Chapter4) 11points a)Give the Gibbs phase rule for the normal case and in case of the constant pressure. Identify all variables in this relation.(2.5 points) b)Draw the tangential line in each of the following G-Ce diagrams(T,p=constant)and label in respective regions the most stable phases.(4 points) c)Based on the given curves of G -cs (at four temperatures TI to T4),construct a qualitative phase diagram and mark all the phase regions (like L,a,B and so on).(2 points) d)How much is the solubility limit at T=OK?Explain your answer by drawing cuves of the enthalpy H(c),the entropy S(c)and the Gibbs free energy G(c)as a function of the solute concentration c in a graph.(2.5 points) 2
2 A3: Low Angle Grain Boundaries (Chapter 3) 8.5 points a) Calculate the number of dislocations per unit length (or rather the length of the dislocation per unit area) in a symmetrical tilt boundary at a misorientation of the neighbouring grains of 1° (b = 2·10-10m). (2.5 points) b) Calculate the energy per area of a low angle tilt boundary as a function of the tilt angle θ. The line energy of a dislocation is: E Gb R r V = − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ + ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2 4 1 0 1 π ν ( ) 2 ln with r0 = 2b and R = d (d = dislocation spacing). (3 points) c) For which tilt angle (in degree) is the specific grain boundary energy maximal? (2 points) d) During the plastic deformation in a material, dislocations are formed beside other defects, so that after deformation many single dislocations are present. Explain with TWO key points, how the crystal reduces the stored energy of the dislocations. (1 point) A4: Alloying (Chapter4) 11points a) Give the Gibbs phase rule for the normal case and in case of the constant pressure. Identify all variables in this relation. (2.5 points) b) Draw the tangential line in each of the following G - cΒ diagrams (T, p = constant) and label in respective regions the most stable phases. (4 points) c) Based on the given curves of G - cB (at four temperatures T1 to T4), construct a qualitative phase diagram and mark all the phase regions (like L, α, β and so on). (2 points) d) How much is the solubility limit at T= 0K? Explain your answer by drawing cuves of the enthalpy H(c), the entropy S(c) and the Gibbs free energy G(c) as a function of the solute concentration c in a graph. (2.5 points)
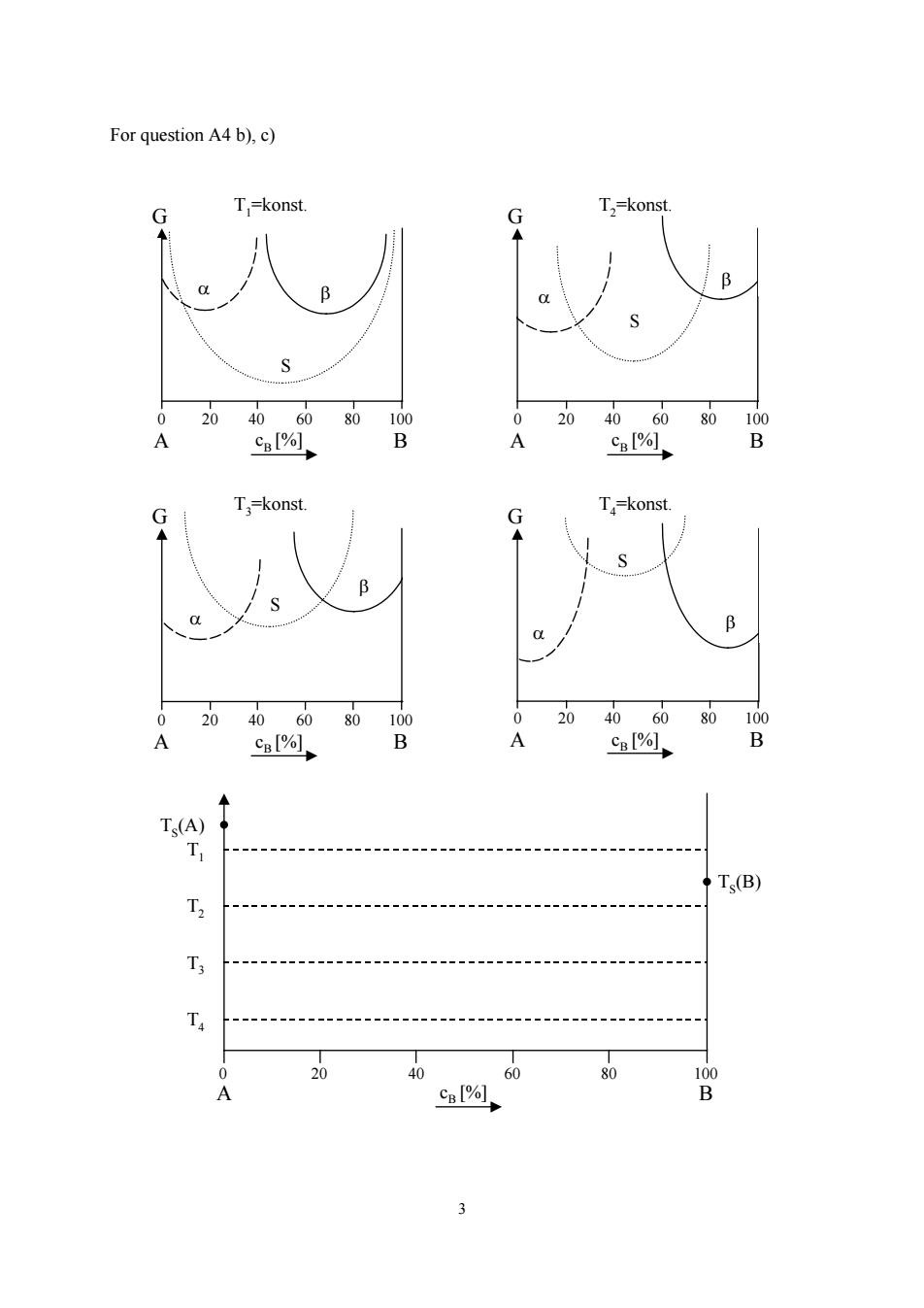
For question A4 b),c) G T,=konst. G T,=konst. B 0 20 4060 80 100 0 20 40 60 80 100 A CB[%]. B A cB[%] B T,=konst. G G T-konst. B 0 20 4060 80 100 0 2040 60 80 100 A c购1, B A %, B Ts(A Ts(B) T2 人 T 0 20 40 60 80 100 A cB[%]、 B
3 For question A4 b), c) G T3=konst. G T4=konst. S α β β S α 0 20 40 60 80 100 A B cB [%] 0 20 40 60 80 100 A B cB [%] G T1=konst. G T2=konst. S α β β α S 0 20 40 60 80 100 A B cB [%] 0 20 40 60 80 100 A B cB [%] T4 T3 T2 T1 TS(A) TS(B) 0 20 40 60 80 100 A B cB [%]

A5:Diffusion (Chapter 5) 5.5 points A cylindrical pressure vessel of nitrogen contains a membrane with a thickness of Ax, which is made of BCC-Fe.Inside the pressure vessel on the left side of the membrane exists a constant concentration of 0.8x102 N-atoms/m'and on the right side exists a concentration of 0.03x1026N-atoms/m3.Which thickness of the membrane is required in order to allow no more than 1%of nitrogen to flow from the left to the right chamber through the membrane during a stationary diffusion process at 600C for 2 h?Please write down your solution step by step and identify the important used parameters. (N in bcc-Fe:Do=0.0047 cm2/s;Q=76.7 kJ/mol) 1=30cm Fe-membrane R=2.5 cm -△x 0.03-1026N-atoms/m3 0.8-1026 N-atoms/m3 A6:Crystal Plasticity (Chapter 6) 8 points a)Draw the engineering stress-strain diagram (schematic)with continuous transition between elastic and plastic ranges.(2 points) b)Indicate and name the SIX most important characteristic quantities in this diagram.(3 points) c)Draw additionally the true stress-strain curve (ot,s after tensile tests)into the engineering stress-strain diagram(in A6 part a).(1 point) d)Write down the mathematic relation between the true and engineering strain and the relation between the true and engineering stress.(2 points) 4
4 A5: Diffusion (Chapter 5) 5.5 points A cylindrical pressure vessel of nitrogen contains a membrane with a thickness of ∆x, which is made of BCC-Fe. Inside the pressure vessel on the left side of the membrane exists a constant concentration of 0.8×1026 N-atoms/m3 and on the right side exists a concentration of 0.03×1026 N-atoms/m3 . Which thickness of the membrane is required in order to allow no more than 1% of nitrogen to flow from the left to the right chamber through the membrane during a stationary diffusion process at 600°C for 2 h? Please write down your solution step by step and identify the important used parameters. (N in bcc-Fe: D0 = 0.0047 cm2 /s; Q = 76.7 kJ/mol) ∆x l = 30 cm R = 2.5 cm 0.8·1026 N-atoms/m3 Fe-membrane 0.03·1026 N-atoms/m3 A6: Crystal Plasticity (Chapter 6) 8 points a) Draw the engineering stress-strain diagram (schematic) with continuous transition between elastic and plastic ranges. (2 points) b) Indicate and name the SIX most important characteristic quantities in this diagram. (3 points) c) Draw additionally the true stress-strain curve (σt, εt after tensile tests) into the engineering stress-strain diagram (in A6 part a). (1 point) d) Write down the mathematic relation between the true and engineering strain and the relation between the true and engineering stress. (2 points)

A7:Dislocation Interactions(Chapter 6) 5 points Calculate the force that is exerted on the dislocation in the sketch below.In which direction will the dislocation move under the influence of this force?How is this kind of dislocation motion called?Does this motion of the dislocation depend on the temperature?Explain your answer in one sentence. →b The line element of the dislocation s is parallel to +z direction A8:Crystal Plastcity and Aging (Chapter 6 9) 20 points a)Name 5 different hardening effects and describe shortly their corresponding dependencies(proportionalities).(5 points) b)The heat treatment is carried out in an aluminium-copper alloy for strengthening,since the small second phase particles can be formed. Briefly describe a suitable temperature path for this heat treatment while taking phase transitions into account.And explain this schematically in the section of Al-Cu phase diagram(Al-rich side).(2.5 points) Temperature [C] L a+L a+Al2Cu AI →wt.%Cu J
5 A7: Dislocation Interactions (Chapter 6) 5 points Calculate the force that is exerted on the dislocation in the sketch below. In which direction will the dislocation move under the influence of this force? How is this kind of dislocation motion called? Does this motion of the dislocation depend on the temperature? Explain your answer in one sentence. F x y z b The line element of the dislocation s is parallel to +z direction A8: Crystal Plastcity and Aging (Chapter 6 & 9) 20 points a) Name 5 different hardening effects and describe shortly their corresponding dependencies (proportionalities). (5 points) b) The heat treatment is carried out in an aluminium-copper alloy for strengthening, since the small second phase particles can be formed. Briefly describe a suitable temperature path for this heat treatment while taking phase transitions into account. And explain this schematically in the section of Al-Cu phase diagram (Al-rich side). (2.5 points) Al wt.% Cu Temperature [°C] α α+ Al2Cu L α+ L

c)Draw the hardness change as a function of time during the heat treatment and explain the phenomena,which cause the hardness change.Divide the hardness curve into 3 characteristic regions.(2.5 points) d)Explain why the equilibrium phase can not be immediately produced during the aging of Al-alloy Additionally calculate the critical nucleus DIAMETER D and the critical nucleation energy A Ge for homogeneous nucleation of spherical nuclei in the solid state.List the relation between the nucleation rate N and nucleation energy AGe(proportionality is enough).(5.5 points) e)Plot both of the stresses in the following diagram:(1 point) Gb Orowan stress(particle radius<<particle spacing):Tor=- F Cutting stress T =y2 b6E r:average particle spacing f:precipitated volume fraction (f-0,03) G:shear modulus b:Burgers Vector Y:effective interface energy (y=120x103 Jm2) E:line energy of dislocation Stress r Radius r 6
6 c) Draw the hardness change as a function of time during the heat treatment and explain the phenomena, which cause the hardness change. Divide the hardness curve into 3 characteristic regions. (2.5 points) d) Explain why the equilibrium phase can not be immediately produced during the aging of Al-alloy. Additionally calculate the critical nucleus DIAMETER Dc and the critical nucleation energy ΔGc for homogeneous nucleation of spherical nuclei in the solid state. List the relation between the nucleation rate N& and nucleation energy ΔGc (proportionality is enough). (5.5 points) e) Plot both of the stresses in the following diagram: (1 point) Orowan stress (particle radius << particle spacing) : τ Or Gb f r = Cutting stress τ γ FK b r f E = 3 2 1 6 r: average particle spacing f: precipitated volume fraction (f=0,03) G: shear modulus b: Burgers Vector γ: effective interface energy (γ=120×10-3 Jm-2) E: line energy of dislocation Radius r Stress τ

f)For which size of precipitates,a maximum stress in case of cuttable particles in COPPER is observed?(Use the values in part e))(3 points) Mark this value qualitatively in the plot in part e)(previous page).(0.5 points) A9:Softening(Chapter 7) 12 points a)Give the definitions and explain briefly the terms "primary recrystallization"and "recovery".(2 points) b)Sketch schematically the relative hardness variation as a function of the recrystallized volume fraction for a material which TENDS to recover and for another which DOES NOT recover.Explain shortly the differences in the behaviour of both materials. Considering the relationship in between,explain the influence of the stacking fault energy.Name for each case an example.(5 points) c)Draw schematically the hardness change during recrystallization depending on the annealing time for two deformation grades s>82 as well as for two annealing temperatures T1>T2.(2 points) d)The back-driving force caused by dispersoids,the so-called Zener-Drag can be described as following: P.=-27Tp The ABNORMAL grain growth occurs in an alloy with the grain size d=0.5um,which contains 0.5 oxide-particles.Particles of which diameter need to be introduced into the material,in order to stop the grain growth (y=1.J/m)?(3 points) (y-grain boundary energy,f-fraction of dispersed oxide-particles,rp-radius of the particles) >
7 f) For which size of precipitates, a maximum stress in case of cuttable particles in COPPER is observed? (Use the values in part e)) (3 points) Mark this value qualitatively in the plot in part e) (previous page). (0.5 points) A9: Softening (Chapter 7) 12 points a) Give the definitions and explain briefly the terms ”primary recrystallization“ and ”recovery”. (2 points) b) Sketch schematically the relative hardness variation as a function of the recrystallized volume fraction for a material which TENDS to recover and for another which DOES NOT recover. Explain shortly the differences in the behaviour of both materials. Considering the relationship in between, explain the influence of the stacking fault energy. Name for each case an example. (5 points) c) Draw schematically the hardness change during recrystallization depending on the annealing time for two deformation grades ε1> ε2 as well as for two annealing temperatures T1>T2. (2 points) d) The back-driving force caused by dispersoids, the so-called Zener-Drag can be described as following: p r r f p γ 2 3 = − The ABNORMAL grain growth occurs in an alloy with the grain size d = 0.5µm, which contains 0.5 % oxide-particles. Particles of which diameter need to be introduced into the material, in order to stop the grain growth (γ = 1J/m2 )? (3 points) (γ - grain boundary energy, f – fraction of dispersed oxide-particles, rp – radius of the particles)

A10:Solidification(Chapter 8) 4.5 points A binary alloy with the concentration of co is solidified in an elongated crucible,during which the heat is removed through the mold wall.The diffusion in both the crystal and the melt proceeds sufficiently fast(De->o and Dm->o). In the following diagram,sketch the concentration and temperature profile at the given time point(at the position of the solidification front).And also plot the expecting tendency of the concentration(dotted line)in completely solidified crystal.Explain the tendency of the concentration with a few words. Kristall Schmelze C2- C2 Co C2 c0- Co CB C1- T T, 人
8 A10: Solidification (Chapter 8) 4.5 points A binary alloy with the concentration of c0 is solidified in an elongated crucible, during which the heat is removed through the mold wall. The diffusion in both the crystal and the melt proceeds sufficiently fast (Dc → ∞ and Dm → ∞). In the following diagram, sketch the concentration and temperature profile at the given time point (at the position of the solidification front). And also plot the expecting tendency of the concentration (dotted line) in completely solidified crystal. Explain the tendency of the concentration with a few words. c0 c2 c1 T2 T1 cB c1 c2 c0 Kristall Schmelze c1 c2 c0 T1 T2 T1 T2 x

A11:Physical Properties(Chapter 10) 4.5 points The specific electrical resistivity pof pure copper at an ambient temperature(20C)is given as 1.67x106 Qcm.Calculate the specific electrical conductivity at 100C, assuming that a specific electrical resistivity is 5.929x10Qcm at 400C. R=8.3144J/molK,k=8.6210-5eV/K=1.3810-23J/K,N=6.023-1023 Material Constants for Aluminium: G=27x10NW/m2,a=4.04A,Tm=660℃,p=2.7gcm3,A-27.0g/mol,v=0.34 YSFE=18x10-2J/m2.YGB-0.6J/m2 Material Constants for Copper: G=48x109N/m2,a=3.61ATm=1083℃,p=8.7gcm3,A=63.5g/mol,V=0.35 YSFE-5x10-2J/m2,YGB-0.5J/m2,YSurface=1J/m2 9
9 A11: Physical Properties (Chapter 10) 4.5 points The specific electrical resistivity ρ of pure copper at an ambient temperature (20°C) is given as 1.67×10–6 Ωcm. Calculate the specific electrical conductivity σ at 100°C, assuming that a specific electrical resistivity is 5.929×10–6 Ωcm at 400°C. R=8.3144 J/molK, k=8.62⋅10-5eV/K = 1.38⋅10-23J/K, NL=6.023⋅1023 Material Constants for Aluminium: G=27×109N/m2, a=4.04Å, Tm=660°C, ρ=2.7g/cm3, A=27.0g/mol, ν=0.34 γSFE=18×10-2J/m2, γGB=0.6J/m2 Material Constants for Copper: G=48×109 N/m2, a=3.61Å, Tm=1083°C, ρ=8.7g/cm3, A=63.5g/mol, ν=0.35 γSFE=5×10-2J/m2, γGB=0.5J/m2, γSurface=1J/m2