
第二章误差理论与数据处理 一、测量误差的基本理论 实验结果-实验数据…与其理论期望值不完全相同 1、测量误差的定义: 测量所得数据与其相应的真值之差-1)绝对误差 测量误差=测得值-真值 x-xo 客观真实值(未知) ①约定真值:世界各国公认的几何量和物理量的最高基准的量值 如:米-公制长度基准 光在真空中1s时间内传播距离的1/299792485(较新) 1m=1650763.73元 2-氪-86的能级间跃迁在真空中的辐射波长 ② 理论真值:设计时给定或用数学、物理公式计算出的给定值(△内角和) ③相对真值:标准仪器的测得值或用来作为测量标准用的标准器的值
第二章 误差理论与数据处理 一、测量误差的基本理论 1、测量误差的定义: 测量误差 = 测得值 - 真值 客观真实值(未知) 1m = 1650763.73 实验结果 --- 实验数据 --- 与其理论期望值不完全相同 ① 约定真值:世界各国公认的几何量和物理量的最高基准的量值 ③ 相对真值:标准仪器的测得值或用来作为测量标准用的标准器的值 如:米 --- 公制长度基准 --- 氪-86的能级间跃迁在真空中的辐射波长 测量所得数据与其相应的真值之差 --- 1)绝对误差 x = x – x0 ② 理论真值:设计时给定或用数学、物理公式计算出的给定值(Δ内角和) 光在真空中1s时间内传播距离的1/299792485(较新)
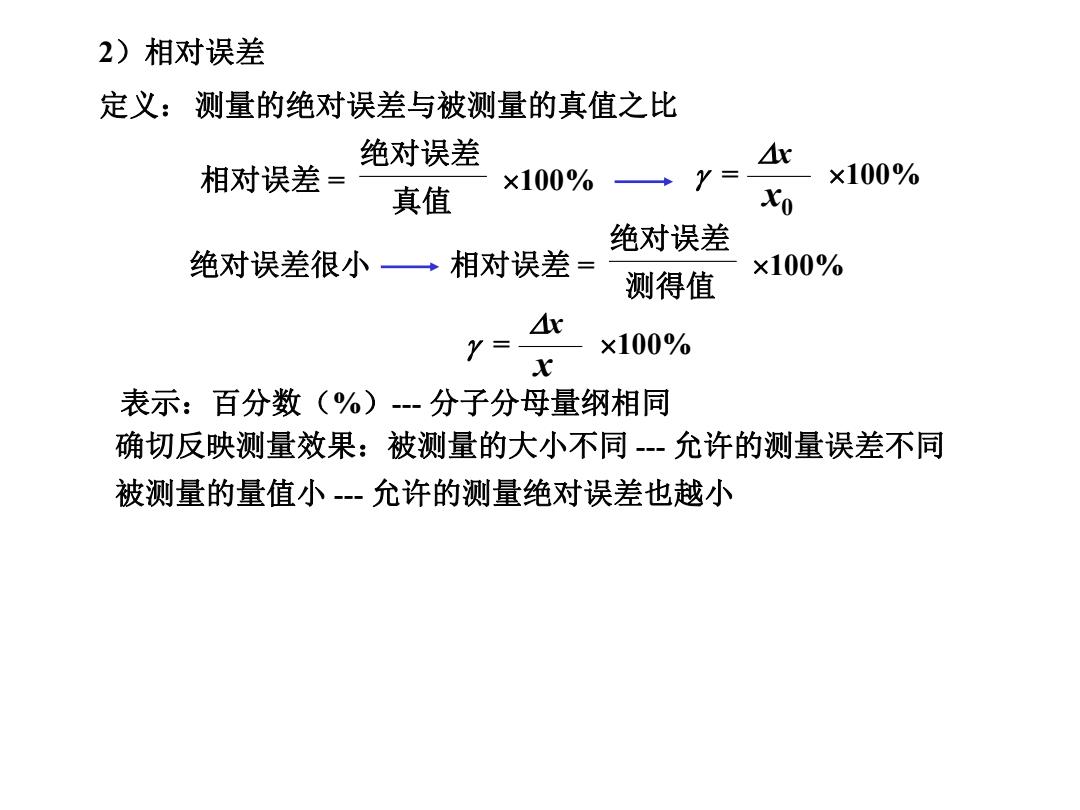
2)相对误差 定义:测量的绝对误差与被测量的真值之比 绝对误差 比 相对误差= x100%→ Y= ×100% 真值 Xo 绝对误差 绝对误差很小·相对误差 = ×100% 测得值 r Y= x100% X 表示:百分数(%)-分子分母量纲相同 确切反映测量效果:被测量的大小不同--允许的测量误差不同 被测量的量值小-允许的测量绝对误差也越小
= 100% = 100% x x0 2)相对误差 测量的绝对误差与被测量的真值之比 绝对误差很小 定义: 表示:百分数(%)--- 分子分母量纲相同 相对误差 = 100% 绝对误差 真值 相对误差 = 100% 绝对误差 测得值 x x 确切反映测量效果:被测量的大小不同 --- 允许的测量误差不同 被测量的量值小 --- 允许的测量绝对误差也越小

2、误差原因 与检测系统的组成和各组成环节有关 ① 由被测对象本身引起的误差 性质、状态、条件以及被测量的种类、状态 ② 因检测理论的假定产生的误差 实际情况与假定情况不符 ③ 检测系统各环节所使用的材料性能和制造技术引起的误差 ④ 组成检测系统各环节的传递特性方面产生的误差 ⑤ 检测系统各环节动力源的变化引起的误差 电流、电压、气压、液压等 ⑧ 检测系统器件特性变化引起的误差--偏离设定值 ⑦ 检测环境引起的误差 环境条件(温度、湿度、气压等)差异一 器件的性能 ⑧检测方法误差 检测方法、采样方法、测量重复次数、取样时间一方法误差 ⑨ 检测人员造成的误差 人员视觉、读数误差、经验、熟练程度、精神方面原因(疲劳)
与检测系统的组成和各组成环节有关 2、误差原因 性质、状态、条件以及被测量的种类、状态 ③ 检测系统各环节所使用的材料性能和制造技术引起的误差 ⑤ 检测系统各环节动力源的变化引起的误差 ⑥ 检测系统器件特性变化引起的误差 --- 偏离设定值 ⑦ 检测环境引起的误差 ⑧ 检测方法误差 ⑨ 检测人员造成的误差 ① 由被测对象本身引起的误差 ② 因检测理论的假定产生的误差 实际情况与假定情况不符 ④ 组成检测系统各环节的传递特性方面产生的误差 人员视觉、读数误差、经验、熟练程度、精神方面原因(疲劳) 环境条件(温度、湿度、气压等)差异 器件的性能 电流、电压、气压、液压等 检测方法、采样方法、测量重复次数、取样时间 方法误差

3、误差分类 按变化速度:静态误差、动态误差 按误差的性质和特征分类:系统误差、随机误差、粗大误差 ① 系统误差(System error)-有规律可循 由特定原因引起、具有一定因果关系并按确定规律产生的测量误差 装置、环境、动力源变化、人为因素 再现性-形成测量值的偏差(Deviation) 可作理论分析/实验验证--找到原因和规律-减少/消除 ② 随机误差(Random error). 因许多不确定性因素而随机发生的误差 许多偶然性(不明确、无规律)原因引起 常对其作概率和统计性处理(无法消除/修正) ③粗大误差(Abnormal error) 检测系统各组成环节发生异常和故障等引起的误差 异常误差可能混为系统误差和偶然误差,使测量结果失去意义 分离开来,防止发生
3 、误差分类 ① 系统误差(System error) 由特定原因引起、具有一定因果关系并按确定规律产生的测量误差 按误差的性质和特征分类:系统误差、随机误差、粗大误差 --- 有规律可循 装置、环境、动力源变化、人为因素 再现性 ---形成测量值的偏差(Deviation) 可作理论分析/实验验证 --- 找到原因和规律 --- 减少/消除 ② 随机误差(Random error) 因许多不确定性因素而随机发生的误差 许多偶然性(不明确、无规律)原因引起 常对其作概率和统计性处理(无法消除/修正) ③ 粗大误差(Abnormal error) 检测系统各组成环节发生异常和故障等引起的误差 异常误差可能 混为系统误差和偶然误差 ,使测量结果失去意义 分离开来,防止发生 按变化速度:静态误差、动态误差

4、检测精度 -检测系统的基本内容 不同场合-检测精度要求不同 例:服装裁剪(身长/胸围)--半厘米;发动机活塞直径-微米级 精度高--系统复杂--造价高 精度按误差原因分类: ①正确度:表征测量结果接近真值的程度 -系统误差大小的反映 ② 精密度:反映测量结果的分散程度(针对重复测量而言) --表示随机误差的大小 ③ 准确度:表征测量结果与真值之间的一致程度 -系统误差和随机误差的综合反映 例: 坐标原点-真值点的位置 点多次测量结果 (a) (b) (c) 图2-8 准确度与精密度
4、检测精度 --- 检测系统的基本内容 不同场合 --- 检测精度要求不同 例:服装裁剪(身长/胸围)--- 半厘米;发动机活塞直径 --- 微米级 精度高 --- 系统复杂 --- 造价高 --- 系统误差大小的反映 坐标原点 --- 真值点的位置 精度按误差原因分类: 点 --- 多次测量结果 ① 正确度:表征测量结果接近真值的程度 ② 精密度:反映测量结果的分散程度(针对重复测量而言) --- 表示随机误差的大小 ③ 准确度:表征测量结果与真值之间的一致程度 --- 系统误差和随机误差的综合反映 例:

二、数据处理的一般方法 数据处理是为求被测量最接近真值的估计值,并作可信程度评定 1、系统误差的消除 ①找出规律--修正值 ②测量方法--避免出现系统误差 2、粗大误差的减少办法和剔除 显然与事实不符-歪曲测量结果-主观避免--剔除(发现) 3、随机误差的分析处理-统计方法 1)分布:正态分布(高斯分布)--大多数; 均匀分布-量化误差、舍入误差; 其它--正弦分布、二次分布、卡方分布、指数分布等 2)主要特征量: 数学期望(Expectation)4--随机变量的总体期望u就是其真值xo 标准偏差(Standard deviation)o--测量精密度的标志
1、系统误差的消除 ② 测量方法 --- 避免出现系统误差 数据处理 是为求被测量最接近真值的估计值 ,并作可信程度评定 ① 找出规律 --- 修正值 二、数据处理的一般方法 2、粗大误差的减少办法和剔除 显然与事实不符 --- 歪曲测量结果 --- 主观避免 --- 剔除(发现) 3、随机误差的分析处理--- 统计方法 正态分布(高斯分布) --- 大多数; 其它 --- 正弦分布、二次分布、卡方分布、指数分布等 1)分布: 均匀分布 --- 量化误差、舍入误差; 数学期望(Expectation ) --- 随机变量的总体期望 就是其真值x0 标准偏差(Standard deviation) --- 测量精密度的标志 2)主要特征量:
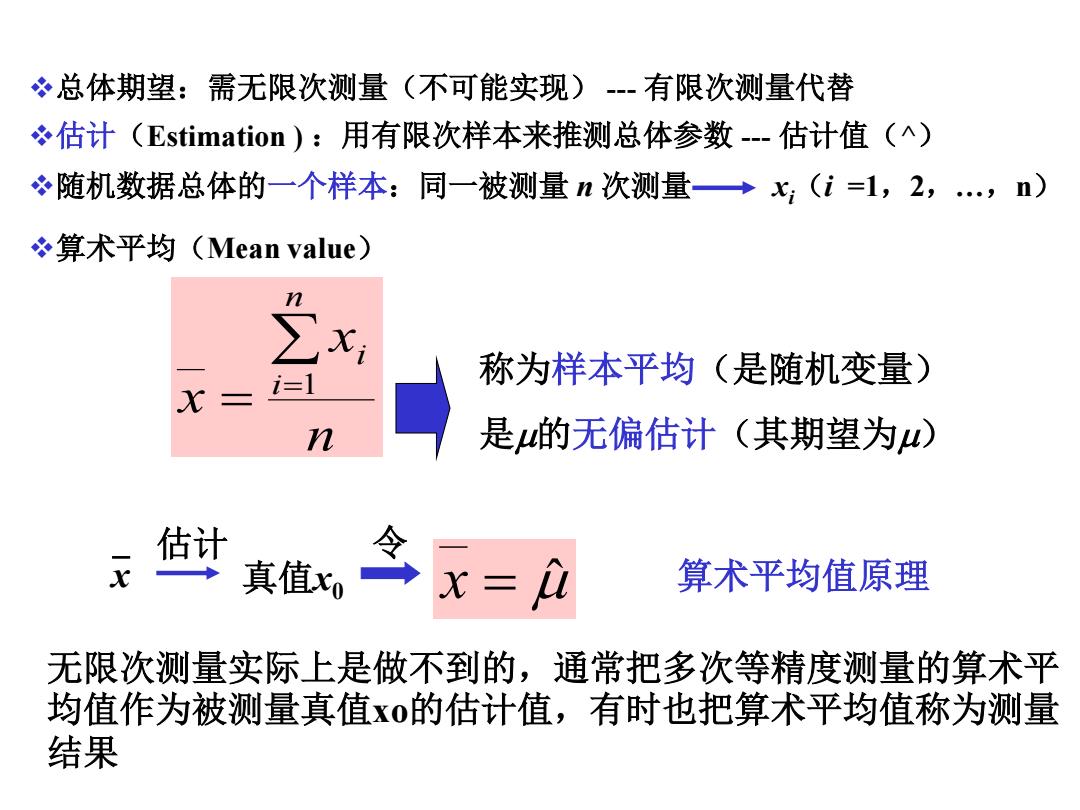
·总体期望:需无限次测量(不可能实现)--有限次测量代替 估计(Estimation):用有限次样本来推测总体参数-估计值(^) 随机数据总体的一个样本:同一被测量n次测量→x:(i=1,2, ...n) 冬算术平均(Mean value) ∑ Xi i=1 称为样本平均(是随机变量) X n 是的无偏估计(其期望为4) 估计 真值x x= 算术平均值原理 无限次测量实标上是做不到的,通常把多次等精度测量的算术平 均值作为被测量真值x0的估计值,有时也把算术平均值称为测量 结果
x 真值x0 估计 x ˆ 算术平均(Mean value) n x x n i i 1 称为样本平均(是随机变量) 是的无偏估计(其期望为) 总体期望:需无限次测量(不可能实现) --- 有限次测量代替 估计(Estimation ) :用有限次样本来推测总体参数 --- 估计值(^) 随机数据总体的一个样本:同一被测量 n 次测量 xi(i =1,2,…,n) 令 算术平均值原理 无限次测量实际上是做不到的,通常把多次等精度测量的算术平 均值作为被测量真值xo的估计值,有时也把算术平均值称为测量 结果

算术平均值原理 B:=X;-X0 随机误差(无系统误差) ∑e, ∑(x,-x) ∑x i=1 i=1 -X0=灭-X0 n n n lim之e,=0 随机误差的抵偿性 n→o∞ i=1 ∴.limc-xo=u-xo=0 1→o0 ∴.u=X0 令x=2
算术平均值原理 0 0 1 1 1 0 0 1 0 0 0 ( ) lim 0 lim 0 ˆ i i n n n i i i i i i n i n i n x x x x x x x x n n n x x x x x 令 随机误差的抵偿性 随机误差(无系统误差)

算术平均值原理 ·假设对某被测量x进行n次等精度(o1=c2 ==0=)的无系差(e=0)独立测量, 测得数据为 x(i=1,2,…,n) 则该测量列的最佳可信赖值是测量列的 算术平均值,即算术平均值是被测量x数 学期望(真值)M(x)的最佳估计
算术平均值原理 • 假设对某被测量x 进行n次等精度(σ1 =σ2 =...=σn =σ)的无系差(ε = 0 )独立测量, 测得数据为 xi(i=1 , 2 , ... , n) 则该测量列的最佳可信赖值是测量列的 算术平均值,即算术平均值是被测量x数 学期望(真值)M ( x )的最佳估计

算术平均值的特点 ①无偏性:估计值x围绕被估计参数M() 摆动,且M()=M(x) ②有效性:文的摆动幅度比单个测量值x小 ③ 一致性:随着测量次数的增加,灭趋于 被测参数的M(x) ④ 充分性:文包含了样本(测量列)的全 部信息
算术平均值的特点 ① 无偏性:估计值 围绕被估计参数M (x) 摆动,且M ( )= M ( x ) ② 有效性: 的摆动幅度比单个测量值xi小 ③ 一致性:随着测量次数的增加, 趋于 被测参数的M ( x ) ④ 充分性: 包含了样本(测量列)的全 部信息 x x x x x