《电路》课程教学资源（PPT课件）第13章 拉普拉斯变换

第13章 拉普拉斯变换 §1拉普拉斯变换的定义 一.拉氏变换的定义 时域 ft) 称为原函数 复频域Fs) 称为象函数 1.双边拉氏变换 F(s)=fed 正变换 s=o+j@ f0=, 2g。mF(s)e” 反变换 复频率 f)与Fs)一一对应

§ 1 拉普拉斯变换的定义 第13章 拉普拉斯变换 一. 拉氏变换的定义 时域 f(t) 称为 原函数 复频域 F(s) 称为 象函数 1. 双边拉氏变换       = =   +  −  +  − − 反变换 正变换 ( ) 2 1 ( ) ( ) ( ) F s e ds j f t F s f t e dt s t j j s t    s =  + j 复频率 f(t)与F(s)一 一对应

2.单边拉氏变换 ) t∈[0，∞) F(s)=[f(t)e-"dt 正变换 1 2g。F(s)e"ds +j∞ f(t)= t≥0反变换 积分下限从0开始，称为0拉氏变换。 积分下限从0+开始，称为0+拉氏变换。 F(s)=f(t)e-"dt -f(edf(t)e"dr f)=0时此项≠0

      =  =   +  −   − 反变换 正变换 ( ) 0 2 1 ( ) ( ) ( ) 0 F s e ds t j f t F s f t e dt s t j j s t    积分下限从0 − 开始，称为0 − 拉氏变换。 积分下限从0 + 开始，称为0 + 拉氏变换。 f t e dt f t e dt F s f t e dt s t s t s t     − −  − + + − − = + = 0 0 0 0 ( ) ( ) ( ) ( ) f(t)=(t)时此项 0 2. 单边拉氏变换 f(t) t  [0,)

F(s)=ft)edt正变换 简写 F(s)=L[f(t)] 0可Fo加本20反变铁 f(t)=L[F(s)] F(s)称为ft)的象函数，用大写字母表示，如Is)、U(s)。 ft)为原函数用小写字母表示，如it),(t)。 3.拉氏变换存在条件 当o>o时，若f()et存在，则()可进行拉氏变换 称σ。为收敛横坐标。 如f(t)=e,选o>5,则eeor为衰减函数， f(t)的拉氏变换存在

      =  =   +  −   − − 反变换 正变换 ( ) 0 2 1 ( ) ( ) ( ) 0 F s e ds t j f t F s f t e dt s t j j s t           = = − ( ) ( ) ( ) ( ) 1 f t L F s F s L f t 简写 F(s)称为f(t )的象函数，用大写字母表示，如 I(s)、U(s)。 f(t )为原函数用小写字母表示，如i(t ), u(t )。 3. 拉氏变换存在条件 称 为收敛横坐标。 当 时，若 存在，则 可进行拉氏变换， 0 0 0 ( ) ( )     f t e dt f t t   − −  的拉氏变换存在。 如 ， 选 ， 则 为衰减函数， ( ) ( ) 5 5 5 f t f t e e e t t t  − = 

电工中常见信号为指数阶函数，指 f(t)≤Mea t∈[0，o)C为有限实数 ∫lf(t)e"t≤JrMe-(a-crdt M 选o>C,则积分存在 o-C 称er为收敛因子 母业翊征出()34()3,3嫌奥际聿中索濂

称e −t 为收敛因子 电工中常见信号为指数阶函数，指 f (t)  Me Ct t [0,)，C为有限实数 f t e dt Me dt t ( C)t 0 0 ( ) − −   −  −   −   C M − =  选 C ,则积分存在 拉氏变换不存在 ) ( ，) ( 数学中有些函数如 2 t t t e t t  

二.常用函数的拉氏变换 F(S)=f(t)e "d 1.f(t)=(t) tomn-Eco e 2.f(t)=emε(t) He -e-(sta) s+ Lleio ] s-jo 3.f(t)=6(t) Lo1=8t)et=6)t=1

二. 常用函数的拉氏变换 +  − = − 0 1 st e s L e e e dt at at −st  − −  − = 0 [ ] 0 1 ( )  − + + = − s a t e s a s + a = 1   − − = 0 L[ (t)] (t)e dt st     − = + 0 e dt st ( ) ( ) 0 F S f t e dt st  +  − = − 1. f (t) =  (t) 2. f (t) e (t) at − =   s j L e j t − = 1 [ ] =   − − 0 L[ (t)] (t)e dt st   3. f (t) =  (t)  + − = 0 0  (t)dt = 1 s 1 =

4.f(t)=t" tr'fre-fd 00 -st 一St ["t"-e-"dt 当n=1 Lt川= lim e =0 t00 当n=2 21= 2 L]=川t] n. Lt"]= n+1

0 lim = → st n t e t n 4. f (t) = t L t t e dt n n −st   = 0 [ ] st n e s t −   = − 0 d n s t s t n t s e e s t d 0 0    − − = − + t e t s n n std 0 1   − − = [ ] [ ] −1 = n n L t s n L t 2 1 1 [ ] s 当n＝ L t = 3 2 2 2 [ ] s 当n＝ L t = 1 ! [ ] + = n n s n L t

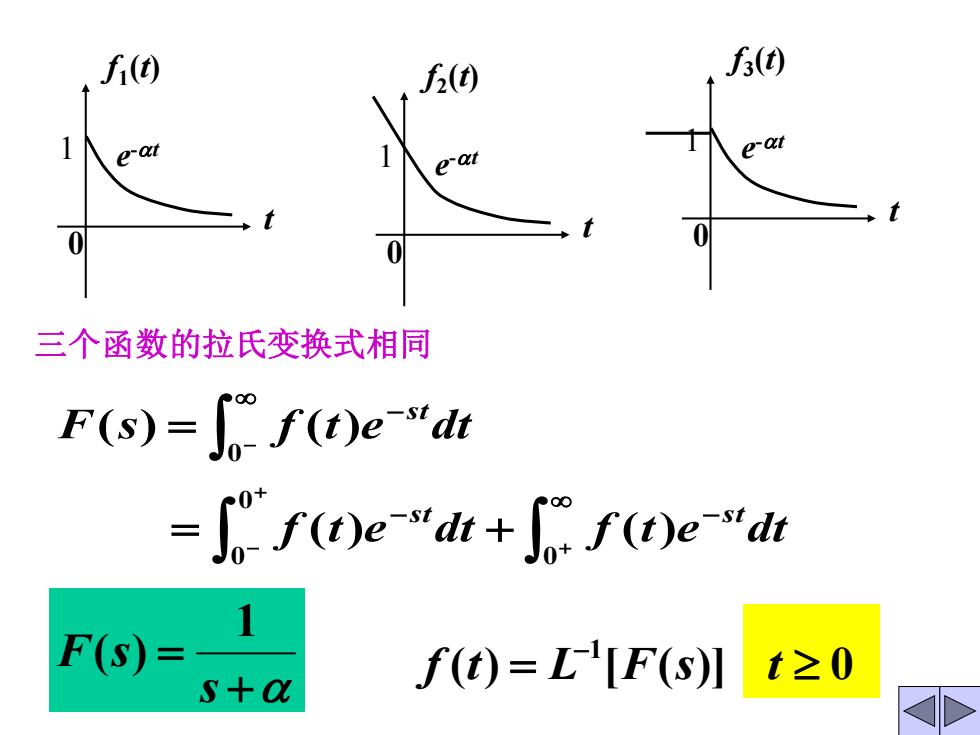
f(因 2() f3() e-at 三个函数的拉氏变换式相同 F(s)=f(t)e-"dt -"f(D)e-"dt+f(e-"dr F(S)= f(t)=L[F(s)1t≥0 s+a

1 f1 (t) e -t t 0 1 f2 (t) e -t t 0 三个函数的拉氏变换式相同 + = s F s 1 ( ) ( ) [ ( )] 0 1 =  − f t L F s t 1 f3 (t) e -t t 0 f t e dt f t e dt F s f t e dt s t s t s t     − −  − + + − − = + = 0 0 0 0 ( ) ( ) ( ) ( )

§2.拉普拉斯变换的基本性质 一.线性性质 若LLf(t]=F(S),LLf(t)】=F(s) 则af(t)±bf(t川=aF(S)士bF(s) 例：IAl= S 耳a-g1=或gd} 3:4sima网=427(e-e1

§ 2.拉普拉斯变换的基本性质 一. 线性性质 [ ( )] ( ) , [ ( )] ( ) 1 1 2 2 若L f t = F s L f t = F s 例1： L[A] 例3： L[sint] [ ( ) ( )] 1 2 则L a f t  b f t ] 1 1 [ 2 1 j S j S + j − − = ( ) ( ) 1 2 = aF s  bF s 2 2   + = S ( )] 2 1 [ j t j t e e j L  −  = − S A = 2 [ (1 )] t L A e − 例 ： − ) 1 1 ( + = − s s A

二.时域导数性质 设：LLf(t川=F(s) 41=-) :Leos1=d（(in@II o dt ) s2+0 例2：460=440=s×g80。-l

二. 时域导数性质 ] ( ) (0 ) ( ) [ − = sF s − f dt df t L [ sin ] 1 2 2 0 − − + = t s s     2 2 + = s s (sin )] 1 1 [cos ] [ t dt d L t L   例 ：  = 例2：L[ (t)] [ (t)] dt d = L  ( ) 1 1 0 =  − t − = S S  设：L[ f (t)] = F(s)

三.时域的积分性质 设：Lf(t川=F(s) f(drl=-F(s) 例L)=可旷(5)d51 L[e(t)_1 S s2

三. 时域的积分性质 ( ) 1 [ ( ) ] 0 F s s L f d t =  −   例 L[t] 2 [ ( )] 1 s s L t = =  [ ( ) ] 0 − = t L   d 设：L[ f (t)] = F(s)