14.6 网络函数 一定义 e(t) 零 r(t⑥ E(s) 态 R(s) 单个独立源作用的线性网络 H(S)= LIr(t)] R(S) Le(t)】 零状态= E(s) 零状态
14.6 网络函数 一. 定义 零状态 零状态 ( ) ( ) L[ ( )] L[ ( )] ( ) E s R s e t r t H s = = 单个独立源作用的线性网络 零 状 态 e(t) r(t) E(s) R(s)
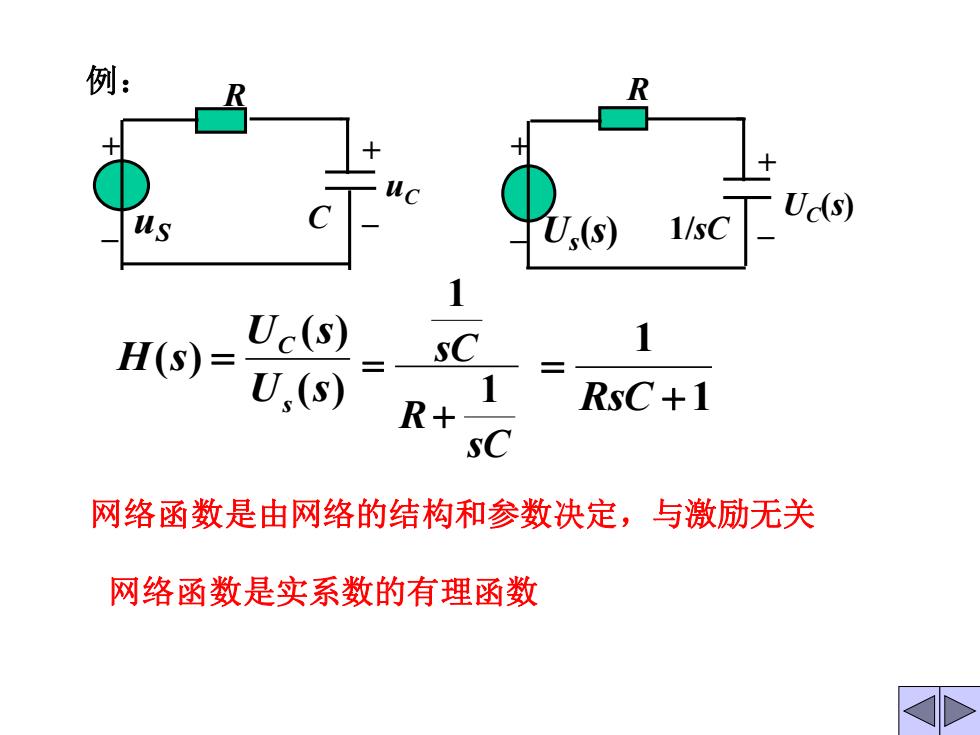
例: us l/sc Ud(s) H(S)= Uc(s) U.(s) R+ RsC+1 网络函数是由网络的结构和参数决定,与激励无关 网络函数是实系数的有理函数
( ) ( ) ( ) U s U s H s s C = sC R sC 1 1 + = 1 1 + = RsC R C + _ + _ uS 例: uC R 1/sC + _ + U _ s (s) UC(s) 网络函数是由网络的结构和参数决定,与激励无关 网络函数是实系数的有理函数
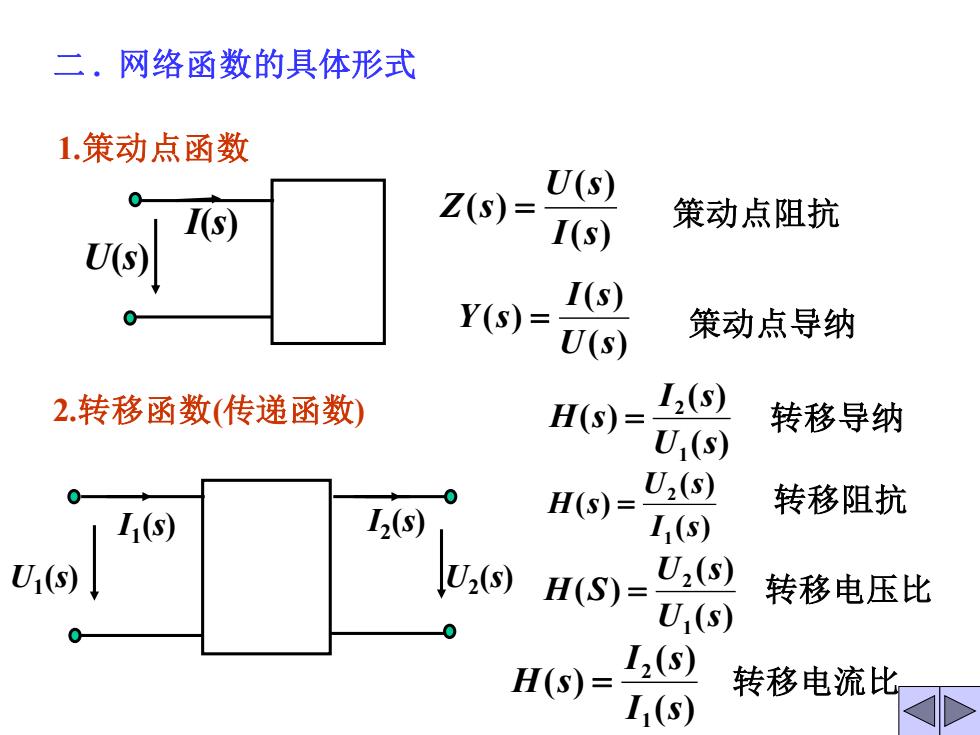
二.网络函数的具体形式 1.策动点函数 U(s) Is) Z(S)= 策动点阻抗 U(s I(s) Y(S)= I(s) U(s) 策动点导纳 2.转移函数(传递函数) H(s)= I2(S) 转移导纳 U1(s) H(S)= U,(s) 转移阻抗 I1(S) L(s) I1(S) U(s) U2) H(S)= U,(s) 转移电压比 U,(s) H(S)= I2(s) 转移电流比 I1(S)
1.策动点函数 ( ) ( ) ( ) I s U s Z s = ( ) ( ) ( ) U s I s Y s = 策动点阻抗 策动点导纳 2.转移函数(传递函数) ( ) ( ) ( ) 1 2 U s I s H s = ( ) ( ) ( ) 1 2 I s U s H s = ( ) ( ) ( ) 1 2 U s U s H S = ( ) ( ) ( ) 1 2 I s I s H s = 转移导纳 转移阻抗 转移电压比 转移电流比 U2 (s) I2 (s) U1 (s) I1 (s) U(s) I(s) 二 . 网络函数的具体形式
三.单位冲激响应、单位阶跃响应与网络函数的关系 6t) h(t) 零状态 e() r(t) H(S)= 〗=(t】 L6(t)川 h(t)=LH(s) 若h()已知,则任意激励产生的响应 h(t)←→H(s) R(s)=E(s)H(s) r(t)=LR(s)
三. 单位冲激响应、单位阶跃响应与网络函数的关系 零状态 (t) h(t) L[ ( )] L[ ( )] L[ ( )] ( ) h t t h t H s = = ( ) L ( ) 1 h t H s − = e(t) r(t) h(t) H(s) R(s) = E(s)H(s) ( ) L ( ) 1 r t R s − = 若h(t)已知,则任意激励产生的响应
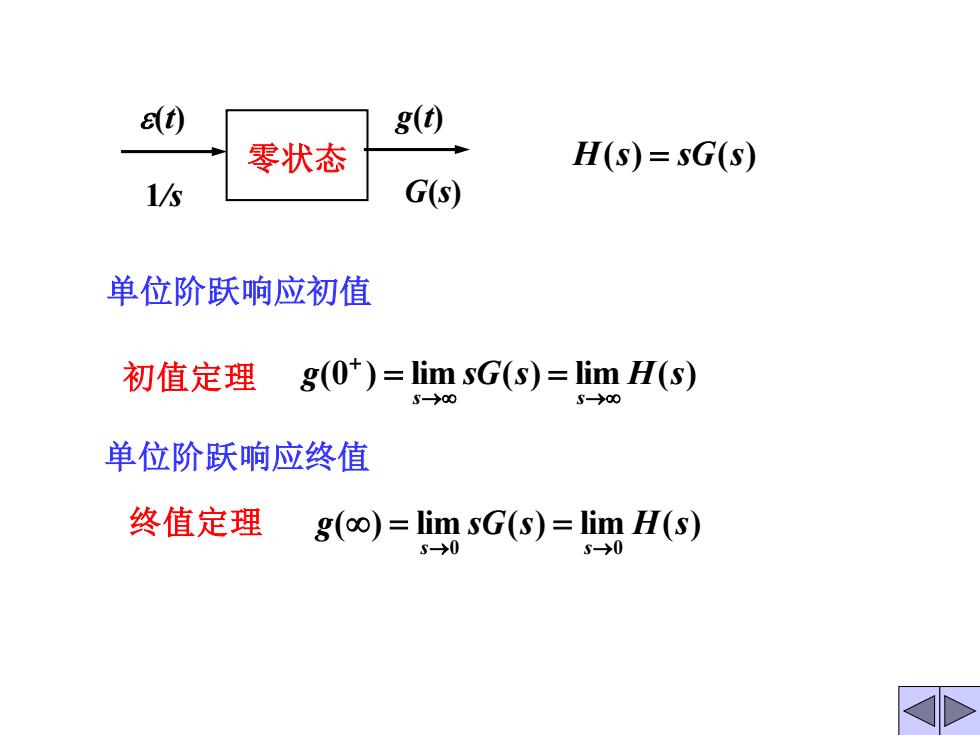
a(t) g() 零状态 H(s)=sG(s) 1/s G(s) 单位阶跃响应初值 初值定理 g(0)=limsG(s)=lim H(s) s->oo 单位阶跃响应终值 终值定理g(o)=imsG(s)=limH(s) s->0
零状态 (t) g(t) 1/s G(s) H(s) = sG(s) g(0 ) lim sG(s) lim H(s) s→ s→ + 初值定理 = = 终值定理 ( ) lim ( ) lim ( ) 0 0 g sG s H s s→ s→ = = 单位阶跃响应初值 单位阶跃响应终值

14.7网络函数的极点和零点 一.复频率平面 S=o+j@ ↑jo H(S)= N(S)_H(S-Z1).(S-Zm) D(S) (S-P).(S-Pn) 当S=Z时H(S)=0称Z1.Zm为零点 当s=P时H(s)=oo称P.Pn为极点 极点用“×”表示,零点用“。”表示
14.7 网络函数的极点和零点 一.复频率平面 j S = + j ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 0 1 n m S P S P H S Z S Z D S N S H S − − − − = = 当S = Zj时H(S) = 0称Z1 Zm为零点 当s = Pi 时H(s) = 称P1 Pn 为极点 极点用“”表示 ,零点用“。”表示。

例: 2(5-2) H(S)= s(s+3)(s2+25+2) 绘出其极零点图 jo H(s)的零点为Z,=2 → H(s)的极点为P=0 0 2 -j P2=-3,P3,4=-1±j1
H(s)的零点为Z1 = 2 j 。 2 -3 3 , 1 1 ( ) 0 2 3,4 1 P P j H s P = − = − 的极点为 = 例: ( 3)( 2 2) 2( 2) ( ) 2 + + + − = s s s s s H s 绘出其极零点图 - 1 j -j 0

二.极点分布与冲激响应 L[h(t)]=H(s) M0=L1s=L2k,nJ s-P 极点位置不同,响应性质不同
二. 极点分布与冲激响应 L[h(t)] = H(s) ( ) L [ ( )] 1 h t H s − = L [ ] 1 1 = − − = n i i i s P k 极点位置不同,响应性质不同

o H(s)= j (s+)2+o2 H(S)= (s2+02 H(S) H,(S)= s+a H:(S)= s-0 X H(S)= 2+w2 X 极点的位置决定冲激响应的波形 极点和零点共同决定冲激响应的的幅值
j s H s i 1 ( ) = s a H s i + = 1 ( ) s a H s i − = 1 ( ) 2 2 ( ) + = s H s i 2 2 ( ) ( ) + + = s a H s i 2 2 ( ) ( ) − + = s a H s i 极点的位置决定冲激响应的波形 极点和零点共同决定冲激响应的的幅值

网络函数极点的位置决定了系统的稳定性 全部极点在左半平面系统是稳定的,只要有一个极点在 右半平面系统不稳定,极点在虚轴上是临界稳定。 网络函数极点是该网络变量的固有频率 R(s)=H(s)E(s) 若 N(s) H(S)= D(s)=0有s,个根 D(s) E(S)= P(s) 2(s)=0有s个根 2(s) 设D(s)和E(s没有相同的极点
网络函数极点的位置决定了系统的稳定性 全部极点在左半平面系统是稳定的,只要有一个极点在 右半平面系统不稳定,极点在虚轴上是临界稳定。 网络函数极点是该网络变量的固有频率 R(s)=H(s)E(s) 若 D s 有si个 根 D s N s H s ( ) 0 ( ) ( ) ( ) = = Q s 有sj个 根 Q s P s E s ( ) 0 ( ) ( ) ( ) = = 设D(s) 和E(s)没有相同的极点