
第六章采用中、大规模 集成电路的逻辑设计
第六章 采用中、大规模 集成电路的逻辑设计

采用$$进行逻辑设计时,逻辑设计和元件 选择是相互独立的,设计追求的目标是最小化, 即尽量减少门和触发器的数量。 采用MSI或LS进行逻辑设计时,最小化也 不再是追求的目标,因为一个器件内门和触发器 的数量是确定的。这种设计方法的关键是以MSI 和LSI器件的功能为基础,从设计要求的逻辑功 能描述出发,合理地选用器件,充分利用器件本 身所具有的功能,减少SSI器件和连线的数量
采用SSI进行逻辑设计时,逻辑设计和元件 选择是相互独立的,设计追求的目标是最小化, 即尽量减少门和触发器的数量。 采用MSI或LSI进行逻辑设计时,最小化也 不再是追求的目标,因为一个器件内门和触发器 的数量是确定的。这种设计方法的关键是以MSI 和LSI器件的功能为基础,从设计要求的逻辑功 能描述出发,合理地选用器件,充分利用器件本 身所具有的功能,减少SSI器件和连线的数量

6.1 6.1二进制并行加法器 二进制并行加法器除能实现二进制加法运 算外,还可实现代码转换、二进制减法运算, 二进制乘法运算,十进制加法运算等功能
6.1 二进制并行加法器 二进制并行加法器除能实现二进制加法运 算外,还可实现代码转换、二进制减法运算, 二进制乘法运算,十进制加法运算等功能。 6.1

Ci A Si B & ≥1 & C P Gi 全加器的逻辑图 C=4BC+4B.C+4BC+4B,C-=PC+G S=4BC+4B.C+4B.C+4B.C =A,©B,©C-1=P田C- P=A⊕BG,=AB C=4B,+BC+4C P=4+B G=AB
i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i P A B G A B A B C P C S A BC A BC A BC A BC C A BC A BC A B C A BC PC G = = = = = + + + = + + + = + − − − − − − − − − − − 1 1 1 1 1 1 1 1 1 1 1 全加器的逻辑图 C i - 1 S i Ai Bi & C i =1& 1 =1 P i G i Ci = Ai Bi + Bi Ci − 1 + Ai Ci − 1 Pi = Ai + Bi Gi = Ai Bi

超前进位加法器 提高工作速度的途径:设法减小进位信号的传递时间 C =PC+G 进位传递公式 P=4+B G=AB, P=A⊕B G=AB, Co=PC1+Go CI=PCo+G=PPoC-1+PGo+G C2=PCI+G2=P2PPC+PPGo+PG+G2 C3=PC2+G3=P3P2PPoC+P3PPGo+PPGI+P3G2+G3
Ci+1 = Pi Ci + Gi 超前进位加法器 提高工作速度的途径:设法减小进位信号的传递时间 进位传递公式 3 3 2 3 3 2 1 0 1 3 2 1 0 3 2 1 3 2 3 2 2 1 2 2 1 0 1 2 1 0 2 1 2 1 1 0 1 1 0 1 1 0 1 0 0 1 0 C PC G P P PPC P P PG P P G PG G C PC G P PPC P PG P G G C PC G PPC PG G C PC G P A B G A B P A B G A B i i i i i i i i i i i i = + = + + + + = + = + + + = + = + + = + = = = + = − − − −
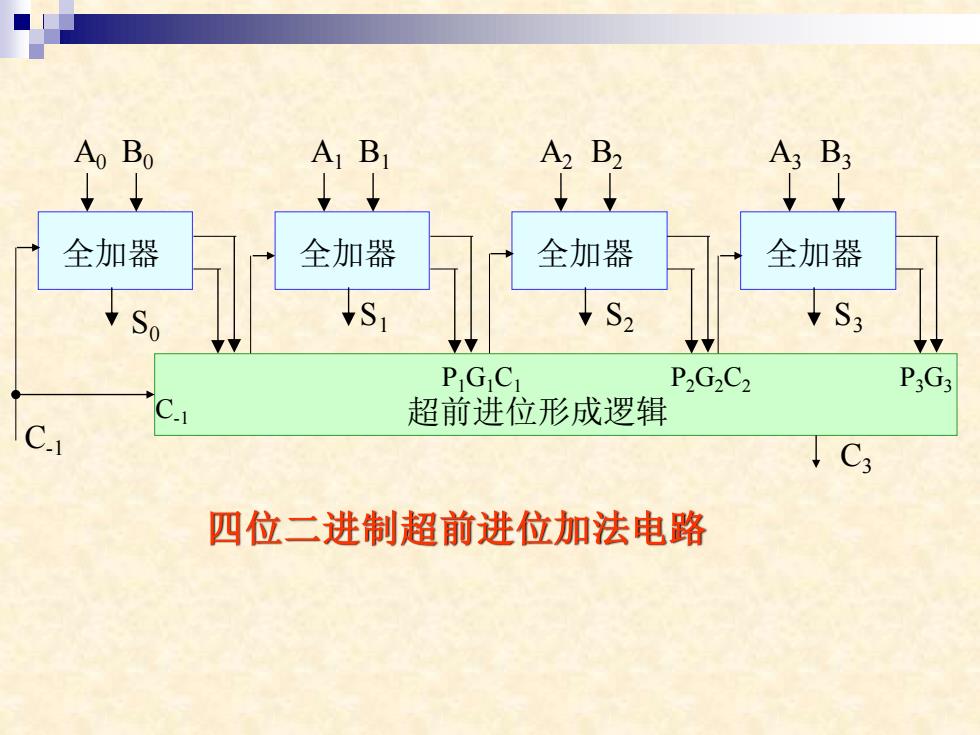
Ao Bo A1 B A2 B2 A3 B3 ↓↓ , g9 全加器 全加器 全加器 全加器 So S S2 1S3 PGjCi P2G2C2 P:G3 C.1 超前进位形成逻辑 C ↓C3 四位二进制超前进位加法电路
四位二进制超前进位加法电路 P0G0C0 S S1 S2 S3 0 A0 B0 A1 B1 A2 B2 A3 B3 全加器 全加器 全加器 全加器 C-1 超前进位形成逻辑 P1G1C1 P2G2C2 P3G3 C-1 C3
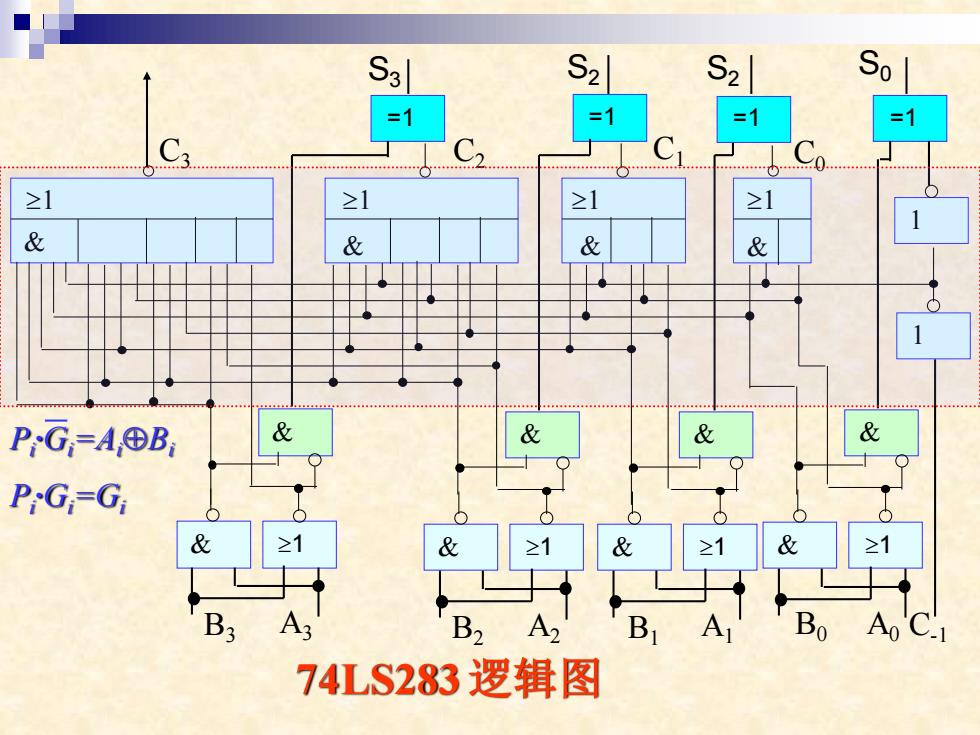
S2S2 So =1 =1 =1 =1 ≥1 & & & PG=A⊕B, & P:G=G 年过 74LS283逻辑图
74LS283 逻辑图 & 1 1 & 1 & 1 & C3 C-1 C0 C2 C1 B3 A3 =1 1 1 & 1 & =1 =1 =1 B1 A1 & 1 & B2 A2 & 1 & B0 A0 & 1 & S3 S2 S2 S0 Pi ∙Gi=AiBi Pi ∙Gi=Gi

例:用四位二进制并行加法器设计一个将 8421BCD码转换成余3码的代转换电路。 解:余3码比8421码多3 余3码 F4 F3 F2 F1 FC4 Co 0” A4 A3 A2 A B4 B3 B2 B1 8421BCD码0011
例: 用四位二进制并行加法器设计一个将 8421BCD码转换成余3码的代转换电路。 余3码比8421码多3 A4 A3 A2 A1 B4 B3 B2 B1 F4 F3 F2 F1 余3码 FC4 C0 8421BCD码 0 0 1 1 “ 0” 解:

例:用四位二进制并行加法器设计一个 四位二进制并行加法/减法器。 解:利用补码,将减法变为加法
例: 用四位二进制并行加法器设计一个 四位二进制并行加法/减法器。 解: 利用补码,将减法变为加法
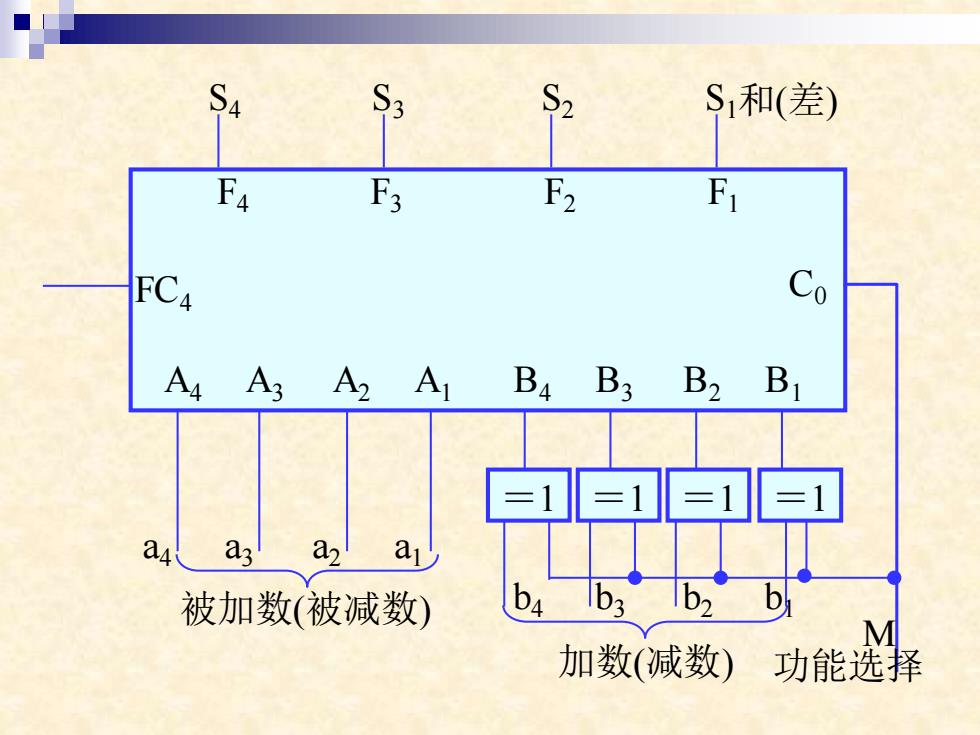
S4 S3 S2 S1和(差) F4 F3 F2 F FC4 Co A4 A3 A2 A Ba B3 B2 B 1=1 a a a 被加数(被减数) ba b3 b2 b M 加数(减数)功能选择
F4 F3 F2 F1 FC4 C0 A4 A3 A2 A1 B4 B3 B2 B1 S4 S3 S2 S1 =1 =1 =1 =1 被加数(被减数) 加数(减数) a4 a3 a2 a1 b4 b3 b2 b1 功能选择 M 和(差)