
第一章 基础知识一信号、噪声和调制 第一节 确知信号的时域和频域描述及分析 一、信号的分类 信号是信息的载体,它表现了物理量的变化。信号的数学 模型是时间函数,书记通信中传输的对象是电信号,非电信号 通过一定形式的转换可成为电信号。 信号从不同的角度可以简单划分为确知信号和随机信号; 周期信号和非周期信号;连续信号和离散信号。 1、确知信号和随机信号 确知信号可以用确定的时间函数来描述。给定一个特定时 刻,就有它相应确定的函数值。 随机信号不能给出确定的时间函数,对于特定时刻不能给 出确切的函数值,只能有概率统计的方法来描述
第一章 基础知识-信号、噪声和调制 第一节 确知信号的时域和频域描述及分析 一、信号的分类 信号是信息的载体,它表现了物理量的变化。信号的数学 模型是时间函数,书记通信中传输的对象是电信号,非电信号 通过一定形式的转换可成为电信号。 信号从不同的角度可以简单划分为确知信号和随机信号; 周期信号和非周期信号;连续信号和离散信号。 1、确知信号和随机信号 确知信号可以用确定的时间函数来描述。给定一个特定时 刻,就有它相应确定的函数值。 随机信号不能给出确定的时间函数,对于特定时刻不能给 出确切的函数值,只能有概率统计的方法来描述

通信系统中传输的信号,一般情况下都是随机信号。 但随机信号有时也可以当做确知信号加以分析,例如数据 信号中常用的二进制代码,虽然二进制代码本身是随机的,但 其中单个的1码和0码,都可以把它看作确知信号。 2、周期信号和非周期信号 周期信号可以定义为 f(t)=f(t±nT) n=0,±1,±2,·. 即信号f按一定的时间间隔T周而复始、无始无终的变化。式 中T称为周期信号的周期。这种信号实际上是不存在的,所 以周期信号只能是在一定时间内按某一规律性重复变化。 非周期信号不具备周而复始的特性,假如周期信号的周期 T值趋向无限大时,它就变成非周期信号。非周期信号从存在 的时域来观察,有可分为时限信号和非时限信号,例如指数函 数f(t)=e3,t≥O是一个非时限信号。非时限信号存 在于一个无界的时域内,时限信号则存在于一个有界的时域内
通信系统中传输的信号,一般情况下都是随机信号。 但随机信号有时也可以当做确知信号加以分析,例如数据 信号中常用的二进制代码,虽然二进制代码本身是随机的,但 其中单个的1码和0码,都可以把它看作确知信号。 2、周期信号和非周期信号 周期信号可以定义为 f (t) = f (t nT) n = 0,1,2, 即信号 f(t) 按一定的时间间隔T周而复始、无始无终的变化。式 中T称为周期信号 f(t) 的周期。这种信号实际上是不存在的,所 以周期信号只能是在一定时间内按某一规律性重复变化。 非周期信号不具备周而复始的特性,假如周期信号的周期 T值趋向无限大时,它就变成非周期信号。非周期信号从存在 的时域来观察,有可分为时限信号和非时限信号,例如指数函 数 , 是一个非时限信号。非时限信号存 在于一个无界的时域内,时限信号则存在于一个有界的时域内, t f t e 3 ( ) − = t 0

例如有一方脉冲信号,其表示式为 2t≤3 03 其函暑只在一定范围内有意义。 3、连续信号和离散信号 连续时间信号时对每个实数t(有限个间断点除外)都由定 义的函数。连续时间信号的幅值可以是连续的,也可以是离散 的(信号含有不连续的间断点属于此类),如图1-1中(a)所 示为幅值连续的连续时间信号,(b)所示为幅值离散的连续 时间信号。 f(t) (t) 图1-1连续时间信号
例如有一方脉冲信号,其表示式为 = 0 3 2 3 ( ) t t f t 其函暑只在一定范围内有意义。 3、连续信号和离散信号 连续时间信号时对每个实数t(有限个间断点除外)都由定 义的函数。连续时间信号的幅值可以是连续的,也可以是离散 的(信号含有不连续的间断点属于此类),如图1-1中(a)所 示为幅值连续的连续时间信号,(b)所示为幅值离散的连续 时间信号
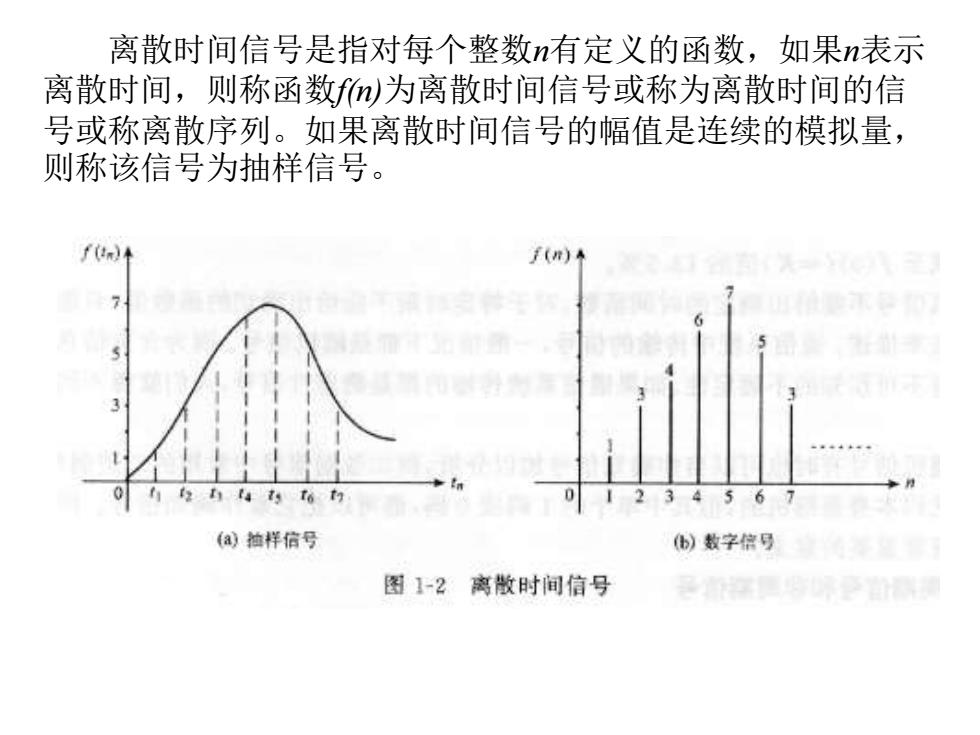
离散时间信号是指对每个整数n有定义的函数,如果n表示 离散时间,则称函数f)为离散时间信号或称为离散时间的信 号或称离散序列。如果离散时间信号的幅值是连续的模拟量, 则称该信号为抽样信号。 (n) f(n)4 (a)抽样信号 )数字信号 图12离散时间信号
离散时间信号是指对每个整数n有定义的函数,如果n表示 离散时间,则称函数f(n)为离散时间信号或称为离散时间的信 号或称离散序列。如果离散时间信号的幅值是连续的模拟量, 则称该信号为抽样信号

二、信号的特性 信号的特性表现为它的时间特性和频率特性。信号的时间 特性主要指信号随时间变化的特性。信号的频率特性可用信号 的频谱方式来表示。 三、确知信号的时域与频域特性 对于确知信号和随机信号都可用它们的时域和频域特性表 示。时域特性表示信号电压或电流随时间变化的关系。所谓频 域或特性即任意信号总可以表示为许多不同频率正弦分量的线 性组合。这些正弦分量的参数(振幅、频率、初相)的规律, 我们称之为该信号的频谱。例如设有一个信号为 f(t)=sin cos@t+sin cos3@t+sm cos5@t 式中01=平,信号f)波形和频谱如图1-3所示
二、信号的特性 信号的特性表现为它的时间特性和频率特性。信号的时间 特性主要指信号随时间变化的特性。 信号的频率特性可用信号 的频谱方式来表示。 三、确知信号的时域与频域特性 对于确知信号和随机信号都可用它们的时域和频域特性表 示。时域特性表示信号电压或电流随时间变化的关系。所谓频 域或特性即任意信号总可以表示为许多不同频率正弦分量的线 性组合。这些正弦分量的参数(振幅、频率、初相)的规律, 我们称之为该信号的频谱。例如设有一个信号为 f t t t t 5 1 1 3 1 1 1 ( ) = sin cos + sin cos3 + sin cos5 T 2 式中 1 = ,信号f(t)波形和频谱如图1-3所示
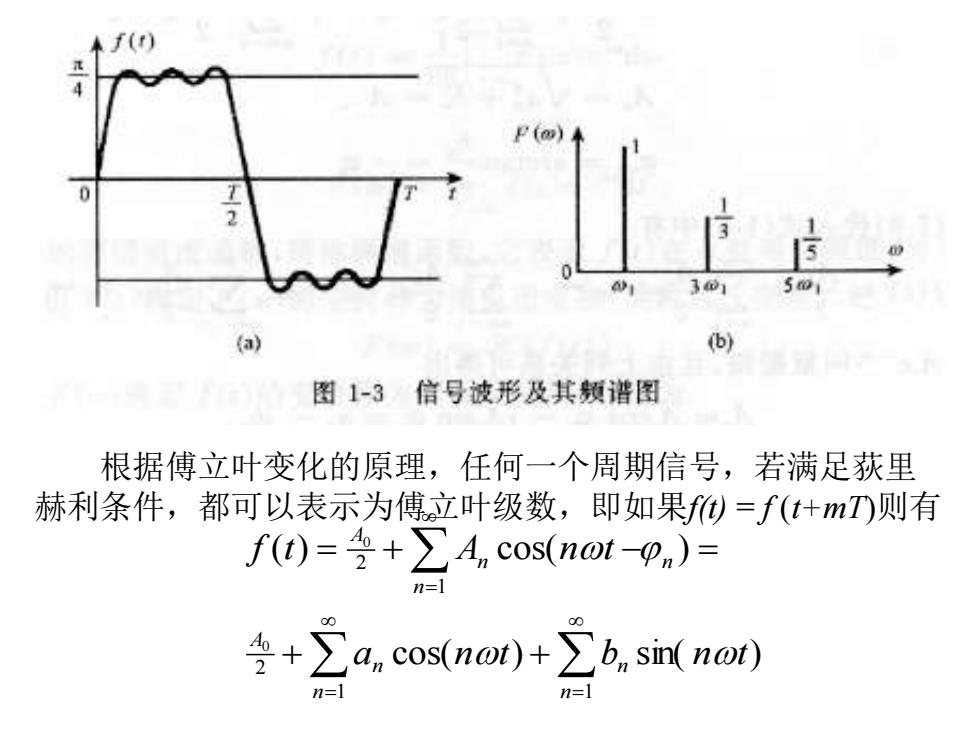
f() P (o) 3⊙ 501 (a)】 (b) 图1-3信号波形及其频谱图 根据傅立叶变化的原理,任何一个周期信号,若满足荻里 赫利条件,都可以表示为傅立叶级数,即如果f=f(t+mT)则有 f(t))=+∑4 cos(not-pn)= n=l ÷+∑a,cos(nor)+2b,sin(not0) n= n=1
根据傅立叶变化的原理,任何一个周期信号,若满足荻里 赫利条件,都可以表示为傅立叶级数,即如果f(t) = f (t+mT)则有 cos( ) sin( ) ( ) cos( ) 1 1 2 1 2 0 0 = = = + + = + − = n n n n A n n n A a n t b n t f t A n t

这里0=严称基波角频率,其中的系数可由下式求得 4-0a (cos(net)de 6=4,sm8,=4=子0saa 并且可知若f为奇函数,则a,=0,若f()为偶函数,则 bn=0。 例如,f如图1-4所示, 求其频谱。 图1-4f)波形图
这里 T 称基波角频率,其中的系数可由下式求得 2 = + = t T t f t dt T A 1 1 ( ) 2 0 + = = = t T t n n n f t n t dt T a A A 1 1 ( ) cos( ) 2 cos 0 + = = = t T t n n n f t n t dt T b A A 1 1 ( )sin( ) 2 sin 0 并且可知若f (t)为奇函数,则an=0,若f (t) 为偶函数,则 bn=0 。 例如,f(t) 如图1-4所示, 求其频谱

为了计算方便,常将傅立叶级数表示成指数形式。 co(mm-) ne-) n= A 2 n=] 2 2 +eme+立2pea 2 上式中 An=Va+b好=Am b P_arctan a
为了计算方便,常将傅立叶级数表示成指数形式。 n jn t j n jn t j n j n t n j n t e e A e e A A e e A A A n t A f t n n n n n n n n n − − − − − − =− − = = = = + + + = + = + − 1 1 0 1 0 1 0 2 2 2 2 2 cos( ) 2 ( ) ( ) ( ) 上式中 n n n n n n n n a b A a b A = = − = + = − − arctan 2 2

f-受+立是eme+2子ee 1三-OO 这里定义An=A,e叫复振幅,且由上列关系可得出 An=An cos pn-jA sin pn=an-jbn 这样函数f可表示 系数A可用下式表示 A-子J臣f(e)emd
j j n t n n j j n t n j j n t n n n e e A e e A e e A A f t n n n − − − − =− − − =− − = = = + + 2 2 2 2 ( ) 1 1 0 这里定义 叫复振幅,且由上列关系可得出 n j n n A A e − = n n n n n n n A = A cos − j A sin = a − j b 这样函数 f(t) 可表示 j n t n f t Ane − =− • = 2 1 ( ) 系数 可用下式表示 • A − − • = 2 2 ( ) 2 T T f t e dt T A j nt

例1-1 设函数f)波形如图1-5所示,求该信号的频谱。 A=2∫f)emat= ∫e not 2 e jugt-ejngt 4 Sin 2 T -ino T no 27 sin n 2 T not sa("g) 2 式中Sa(x)称为抽样函数,作出 该函数的频谱如图1-6所示。 2 4 图1-6f(1)的频谱图
例1-1 设函数 f(t) 波形如图1-5所示,求该信号的频谱。 = = = − − = = = − − − − • − 2 2 sin 2 2 sin 2 4 2 ( ) 2 2 2 2 2 2 2 2 2 n Sa T T n n j n T e e T e dt T f t e dt T A n n n n jn t jn t j j T T 式中 Sa(x) 称为抽样函数,作出 该函数的频谱如图1-6所示