
第3章组合逻辑电路
第3章 组合逻辑电路

第3章组合逻辑电路 3.1概 述 3.2组合逻辑电路的分析 3.3组合逻辑电路的设计 3.4加法器 3.5数值比较器 3.6编码器 3.7译码器 3.8数据选择器 3.9数据分配器 3.10奇偶检测电路 3.11用中规模集成电路设计一般组合电路 3.12组合电路中的竞争冒险
第3章 组合逻辑电路 ◼ 3.1 概 述 ◼ 3.2 组合逻辑电路的分析 ◼ 3.3 组合逻辑电路的设计 ◼ 3.4 加 法 器 ◼ 3.5 数值比较器 ◼ 3.6 编 码 器 ◼ 3.7 译 码 器 ◼ 3.8 数据选择器 ◼ 3.9 数据分配器 ◼ 3.10 奇偶检测电路 ◼ 3.11 用中规模集成电路设计一般组合电路 ◼ 3.12 组合电路中的竞争冒险

3.1概述 ■组合逻辑电路的特点是:输出与输入的关系具有即 时性。即电路在任意时刻的输出状态只取决于该时 刻的输入状态,而与该时刻前的电路状态无关,这 种数字电路称为组合逻辑电路。 ■研究组合电路的任务有3方面 1)对已给定的组合电路分析其逻辑功能。 2)根据逻辑命题的需要,设计组合电路 (3)掌握常用组合单元电路一些中规模器件)的逻辑功 能,选择和应用到工程实际申
3.1 概 述 ◼ 组合逻辑电路的特点是:输出与输入的关系具有即 时性。即电路在任意时刻的输出状态只取决于该时 刻的输入状态,而与该时刻前的电路状态无关,这 种数字电路称为组合逻辑电路。 ◼ 研究组合电路的任务有3方面: (1)对已给定的组合电路分析其逻辑功能。 (2) 根据逻辑命题的需要,设计组合电路。 (3) 掌握常用组合单元电路(一些中规模器件)的逻辑功 能,选择和应用到工程实际中
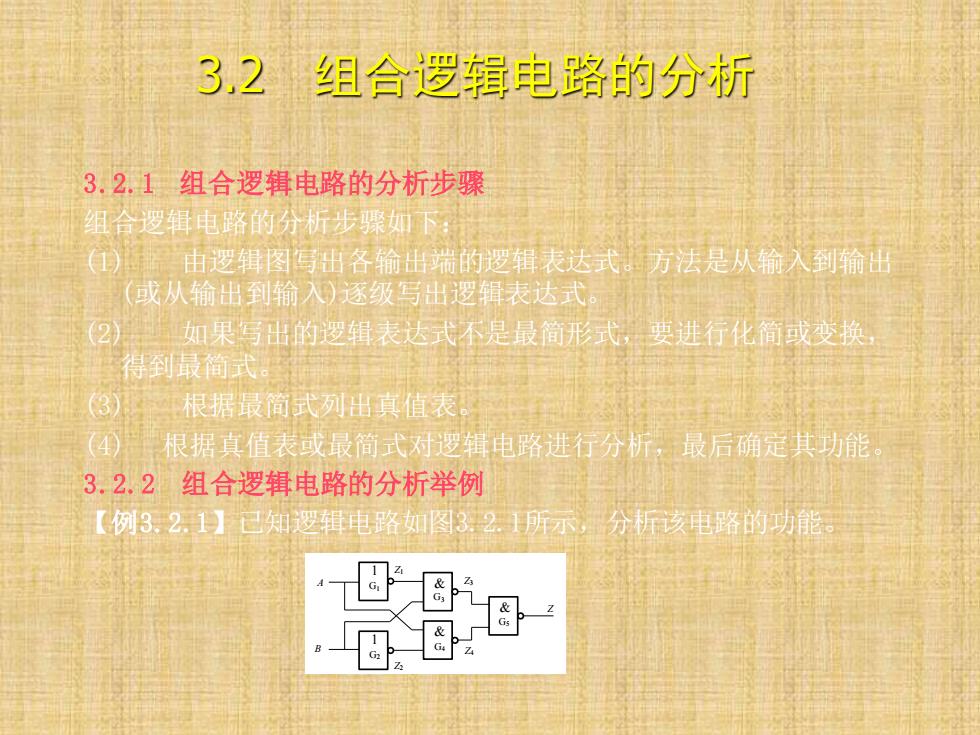
32组合逻辑电路的分析 3.2.1组合逻辑电路的分析步骤 组合逻辑电路的分析步骤如下 自 由逻辑图写出各输出端的逻辑表达式。方法是从输入到输田 (或从输出到输入)逐级写出逻辑表达式。 2 如果写出的逻辑表达式不是最简形式,要进行化简或变换 得到最简武。 3) 根据最简式列出真值表。 (40 根据真值表或最简式对逻辑电路进行分析,最后确定其功能 3.2.2组合逻辑电路的分析举例 【例3.21】已知逻辑电路如图321所示,分标该电路的功能
3.2 组合逻辑电路的分析 3.2.1 组合逻辑电路的分析步骤 组合逻辑电路的分析步骤如下: (1) 由逻辑图写出各输出端的逻辑表达式。方法是从输入到输出 (或从输出到输入)逐级写出逻辑表达式。 (2) 如果写出的逻辑表达式不是最简形式,要进行化简或变换, 得到最简式。 (3) 根据最简式列出真值表。 (4) 根据真值表或最简式对逻辑电路进行分析,最后确定其功能。 3.2.2 组合逻辑电路的分析举例 【例3.2.1】已知逻辑电路如图3.2.1所示,分析该电路的功能。 1 1 & & & A B Z Z1 Z2 Z3 Z4 G1 G2 G3 G4 G5

3.3组合逻辑电路的设计 3.3.1组合逻辑电路的设计步骤 对实际问题进行逻辑抽象,并定议输入变量和输出变量 在实际间题中,凡是引起事件发生的条件和原因的物理量应定 义为输入变量,凡是表示事件发生结果的物理量应定义为输出 变量。 2 根据所要实现的逻辑功能列真值表。将输入变量可能出现 的所有取值情况和与之对应的输出变量的值一一列出 3) 根据真值表求逻辑表达式并化简。根据选用的门电路类型 将逻辑表达式变换成所要的形式,比如,若采用与非门实现 则应将逻辑表达式变换为与非一与非表达式。 40 根据逻辑表达式画逻辑图
3.3.1 组合逻辑电路的设计步骤 (1) 对实际问题进行逻辑抽象,并定义输入变量和输出变量。 在实际问题中,凡是引起事件发生的条件和原因的物理量应定 义为输入变量,凡是表示事件发生结果的物理量应定义为输出 变量。 (2) 根据所要实现的逻辑功能列真值表。将输入变量可能出现 的所有取值情况和与之对应的输出变量的值一一列出。 (3) 根据真值表求逻辑表达式并化简。根据选用的门电路类型 将逻辑表达式变换成所要的形式,比如,若采用与非门实现, 则应将逻辑表达式变换为与非-与非表达式。 (4) 根据逻辑表达式画逻辑图。 3.3 组合逻辑电路的设计

3.3,2组合逻辑电路的设计举例 【例33.1】已知有3个逻辑变量A,B,C,利用与非门设计一个逻辑电 路,判断3个变量中是否有多数个取值为] 解 ①定义输入变量和输出变量。A,B,C,3个变量应为输入变量,设输 出变量为Y。当Y=I时,表明AB.C多数取值为1,否则YO ②根据题意列填值表,见表331 ③根据真值表写出逻辑表达式,化简,并将其变换为“与非一与非 表达式 33.1 Y=ABC+ABC+ABC=AB+AC+BC=AB·AC·BC ④根据逻辑表达式画逻辑图,如图331所示
3.3.2 组合逻辑电路的设计举例 【例3.3.1】已知有3个逻辑变量A,B,C,利用与非门设计一个逻辑电 路,判断3个变量中是否有多数个取值为1。 解 ① 定义输入变量和输出变量。A,B,C ,3个变量应为输入变量,设输 出变量为Y。当Y=1时,表明A,B,C多数取值为1,否则Y=0。 ②根据题意列真值表,见表3.3.1。 ③ 根据真值表写出逻辑表达式,化简,并将其变换为“与非-与非” 表达式。 (3.3.1) ④ 根据逻辑表达式画逻辑图,如图3.3.1所示。 Y = ABC + ABC + ABC = AB + AC + BC = AB AC BC
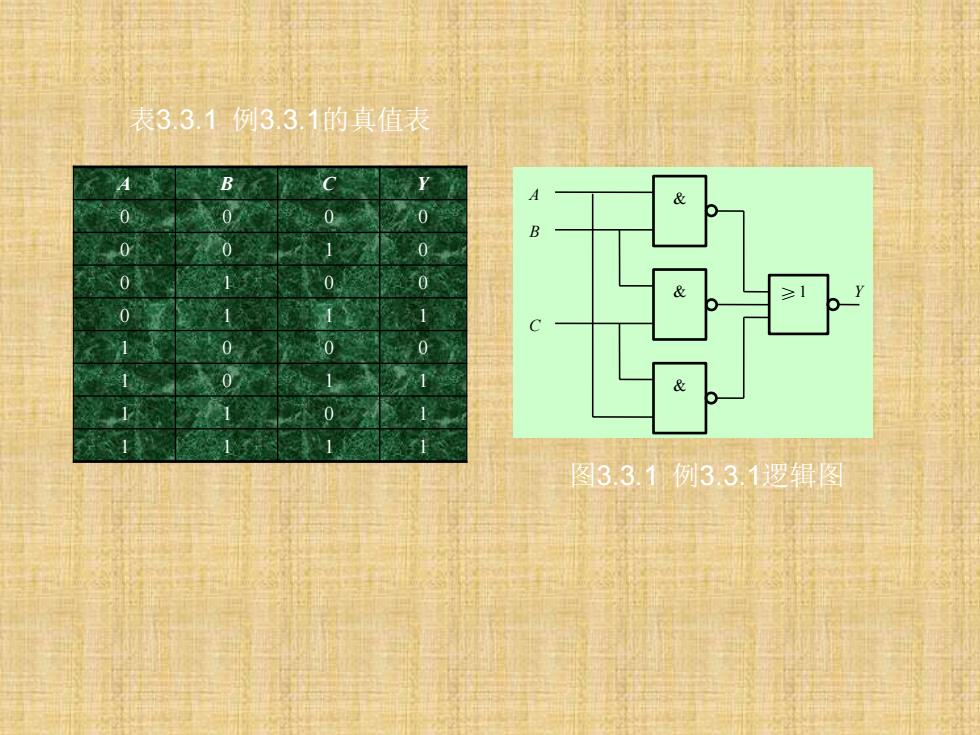
表3.3.1例3.3.1的真值表 B C 0 B 0 1 0 0 0 0 C 0 0 0 0 图33.1例33.1逻辑图
A B C Y 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 表3.3.1 例3.3.1的真值表 Y A B C ≥1 & & & 图3.3.1 例3.3.1逻辑图

3.4加法器 在数字系统中,无其是在计算机的数字系统中 盖进制加法器是宿 的基本部件之 市。 在进行两个进制数之间的算术运算时,无论是 加减、乘、除,最后都可化作加法运算来实现。能够实现加法运 算的电路称为加法器,它是算术运算的基本单元电路 3.4.1半加器和全加器 ,半加器 只考虑两个1位进制数和B相加,不考虑低位来的进位数的相 加称为半加,实现半加的电路称为半加器。半加器的真值表见表 34 表34.1半加器的真值表
3.4 加 法 器 在数字系统中,尤其是在计算机的数字系统中,二进制加法器是它 的基本部件之一。在进行两个二进制数之间的算术运算时,无论是 加、减、乘、除,最后都可化作加法运算来实现。能够实现加法运 算的电路称为加法器,它是算术运算的基本单元电路。 3.4.1 半加器和全加器 1. 半加器 只考虑两个1位二进制数A和B相加,不考虑低位来的进位数的相 加称为半加,实现半加的电路称为半加器。半加器的真值表见表 3.4.1。 输 入 输 出 A B S C 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 表3.4.1 半加器的真值表

半加器的逻辑表达式为 S=AB+AB C=A.B 加器的逻辑符号如图34,1b)所示 (a)逻辑电路 -S HA (b)逻辑符号
__ __ S A B A B C A B = + = 半加器的逻辑表达式为 半加器的逻辑符号如图3.4.1(b)所示 A S B C HA (b)逻辑符号 A B S C (a)逻辑电路 =1 &
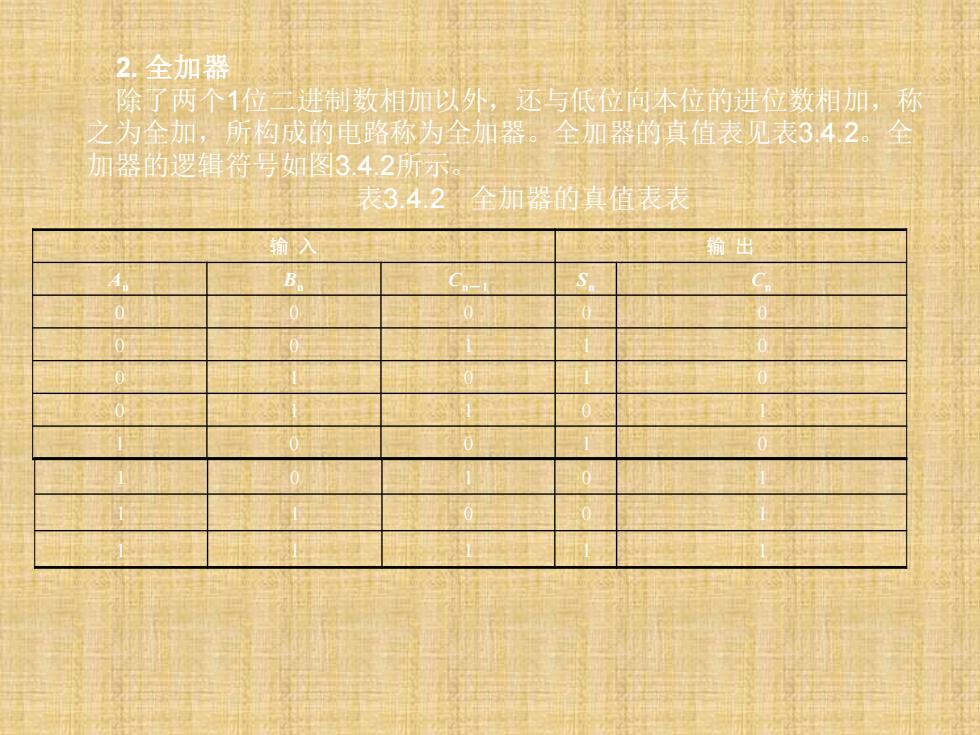
2.全加器 除了两个1位云进制数相加以外,还与低位向本位的进位数相加,称 之为全加,所构成的电路称为全加器。全加器的真值表见表342。全 加器的逻辑符号如图3.42所示。 表342全加器的真值表表 输出 B 0
2. 全加器 除了两个1位二进制数相加以外,还与低位向本位的进位数相加,称 之为全加,所构成的电路称为全加器。全加器的真值表见表3.4.2。全 加器的逻辑符号如图3.4.2所示。 表3.4.2 全加器的真值表表 输 入 输 出 An Bn Cn-1 Sn Cn 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1