
第二章逻辑代数基础
第二章 逻辑代数基础

学习要求: ·掌握逻辑代数的基本概念,学会用逻辑函描 述逻辑问题的基本方法。 ·掌握逻辑代数的公理、基本定理和重要规则; ·学会用代数法化简逻辑函数: ·熟练掌握用卡诺图化简逻辑函数
学习要求: • 掌握逻辑代数的基本概念,学会用逻辑函描 述逻辑问题的基本方法。 • 掌握逻辑代数的公理、基本定理和重要规则; • 学会用代数法化简逻辑函数; • 熟练掌握用卡诺图化简逻辑函数

2.1 2.1逻辑代数的基本概念 逻辑代数是一个由逻辑变量集K,常量0和 1以及“与”、“或”、“非”3种基本运算构 成的一个封闭的代数系统,记为L={K,+,·,-,0, 1}。它是一个二值代数系统。常量0和1表示真 和假,无大小之分。 该系统满足下列公理:
2.1 逻辑代数的基本概念 逻辑代数是一个由逻辑变量集K,常量0和 1以及“与”、“或”、“非”3种基本运算构 成的一个封闭的代数系统,记为L={K, +, •, -, 0, 1}。它是一个二值代数系统。常量0和1表示真 和假,无大小之分。 该系统满足下列公理: 2.1

公理1交换律 A+B=B+A,A·B=B·A 公理2结合律 (A+B)+C=A+(B+C), (A·B)·C=A·(B·C) 公理3分配律 A+(B·C)=(A+B)·(B+C), A(B+C)=A·B+A.C 公理40-1律 A+0=A,A.1=A A+1=1,A·0=0, 公理5互补律 A+A=1,AA=0
公理1 交换律 A+B=B+A, A B=B A 公理2 结合律 (A+B)+C=A+(B+C), (A B) C=A (B C) 公理3 分配律 A+ ( B C ) =(A+B) (B+C), A ( B+C ) =A B+A C 公理4 0-1律 A+ 0 =A, A 1=A A+1=1, A 0=0, 公理5 互补律 A+ A =1, AA=0

2.1.12.1.1逻辑变量及基本逻辑运算 逻辑变量:仅取值0或取值1的变量。这里0和1 无大小之分,实际上代表着矛盾的双方或事件 的真假,例如开关的接通与断开,电压的高和 底,信号的有和无,电灯的亮和灭等等。 只要是两种稳定的物理状态,都可以用0和1这 两种不同的逻辑值来表征
2.1.1 逻辑变量及基本逻辑运算 逻辑变量:仅取值0或取值1的变量。这里0和1 无大小之分,实际上代表着矛盾的双方或事件 的真假,例如开关的接通与断开,电压的高和 底,信号的有和无,电灯的亮和灭等等。 只要是两种稳定的物理状态,都可以用0和1这 两种不同的逻辑值来表征。 2.1.1

一、"或"运算 如果决定某一事件发生的多个条件,只 要有一个或一个以上的条件成立,事件便可发 生,这种因果关系称之为"或"逻辑。在逻辑代 数中,"或"逻辑关系用"或"运算描述。"或"运 算又称逻辑加,其运算符为"+"或"y",两个 变量的"或"运算可表示为: F=A+B或者F=AB 读作"F等于A或B",其中A、B是参加运算的 两个逻辑变量,F为运算结果。意思是:只 要A、B中有一个为1,则F为1;仅当A、B 均为0时,F才为0
一、"或"运算 如果决定某一事件发生的多个条件,只 要有一个或一个以上的条件成立,事件便可发 生,这种因果关系称之为"或"逻辑。在逻辑代 数中,"或"逻辑关系用"或"运算描述。"或"运 算又称逻辑加,其运算符为"+"或" " ,两个 变量的"或"运算可表示为: F=A+B 或者 F=AB 读作"F等于A或B",其中A、B是参加运算的 两个逻辑变量,F为运算结果。意思是:只 要A、B中有一个为1,则F为1;仅当A、B 均为0时,F才为0
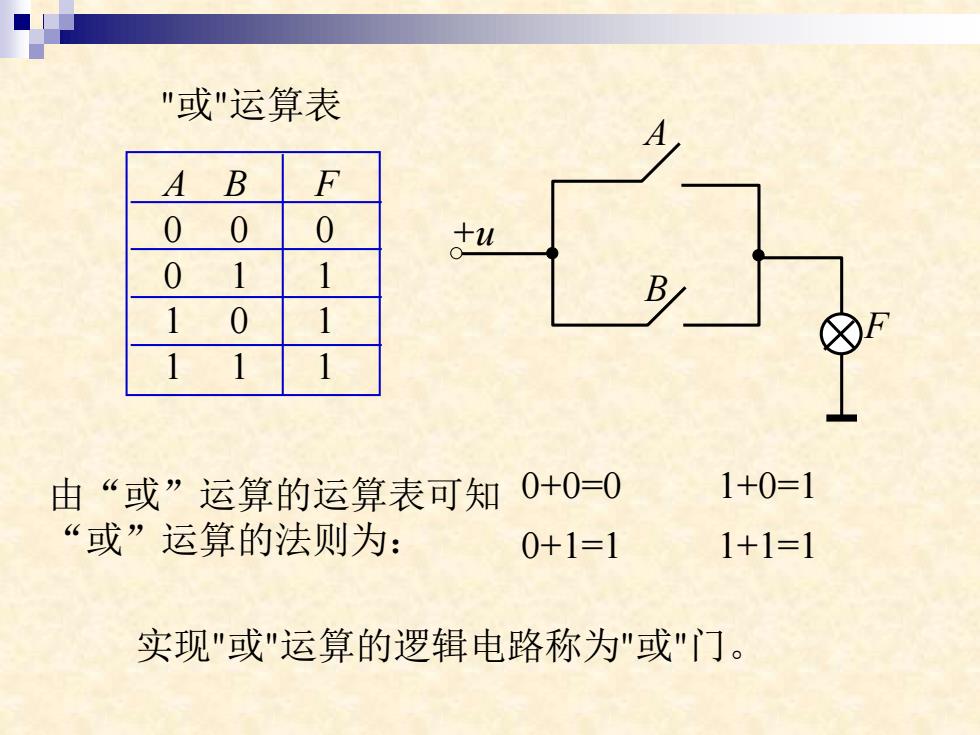
"或"运算表 A B F 0 0 0 tu 0 1 0 由“或”运算的运算表可知0+0=-0 1+0=1 “或”运算的法则为: 0+1=1 1+1=1 实现"或"运算的逻辑电路称为"或"门
A B F 0 0 0 0 1 1 1 0 1 1 1 1 "或"运算表 A +u B F 由“或”运算的运算表可知 “或”运算的法则为: 0+0=0 1+0=1 0+1=1 1+1=1 实现"或"运算的逻辑电路称为"或"门

二、"与"运算 如果决定某一事件的发生的多个条件必须 同时具备,事件才能发生,这种因果关系称为" 与"逻辑。逻辑代数中"与"逻辑关系用"与"运算 描述。"与"运算又称逻辑乘,其运算符为""或 "∧"。两变量的"与"运算可表示为 F=A·B或者F=AAB 读作"F等于A与B",意思是若A·B均为1,则F 为1;否则F为0
二、"与"运算 如果决定某一事件的发生的多个条件必须 同时具备,事件才能发生,这种因果关系称为" 与"逻辑。逻辑代数中"与"逻辑关系用"与"运算 描述。"与"运算又称逻辑乘,其运算符为""或 ""。两变量的"与"运算可表示为 F=A B 或者 F=AB 读作"F等于A与B" ,意思是若A B 均为1,则F 为1;否则F为0

"与"运算表 A B F 0 0 0 0 1 0 1 0 0 F 由“与”运算的运算表可知0·0=0 1·0 0 “与”运算法则为: 0.1=0 1·1=1 实现“与”运算的逻辑电路称为“与”门
A B F 0 0 0 0 1 0 1 0 0 1 1 1 "与"运算表 +u A B F 由“与”运算的运算表可知 “与”运算法则为: 0 0 = 0 1 0 = 0 0 1 = 0 1 1 = 1 实现“与”运算的逻辑电路称为“与”门

三、"非"运算 如果某一事件的发生取决于条件的否定, 则这种因果关系称为"非"逻辑。"非"逻辑用" 非"运算描述。"非"运算又称求反运算,运算 符为"一"或"一"."非"运算可表示为 F=A或F=A 读作"F等于A非",意思是若A=0,则F为1; 反之,若A=1,则F为0
三、"非"运算 如果某一事件的发生取决于条件的否定, 则这种因果关系称为"非"逻辑。"非"逻辑用" 非"运算描述。"非"运算又称求反运算,运算 符为"-"或"¬". "非"运算可表示为 F=A 或 F= ¬A 读作"F等于A非",意思是若A=0,则F为1; 反之,若A=1, 则F为0