
第三章」 组合逻辑电路
第三章 组合逻辑电路

学习要求: •了解组合逻辑电路的特点; •熟练掌握组合电路分析和设计的基本方法; ·了解竞争、冒险的概念; •掌握消除冒险的基本方法
学习要求: •了解组合逻辑电路的特点; •熟练掌握组合电路分析和设计的基本方法; •了解竞争、冒险的概念; •掌握消除冒险的基本方法

定义: 如果一个逻辑电路在任何时刻产生的稳定 输出值仅仅取决于该时刻各输入值的组合,而 与过去的输入值无关,则称该电路为组合逻辑 电路 组合逻辑电路需要讨论的两个基本问题 是分析与设计
定义: 如果一个逻辑电路在任何时刻产生的稳定 输出值仅仅取决于该时刻各输入值的组合,而 与过去的输入值无关, 则称该电路为组合逻辑 电路. 组合逻辑电路需要讨论的两个基本问题 是分析与设计

3.1.1逻辑门电路的逻辑符号及外部特性 3.1.1简单逻辑门电路 实现"与"、"或"、"非"三种基本运算的门电路 称为简单门电路。 F & ≥1 A B AB A (a) (b) (c) 高电平:+5v 低电平:0v 正逻辑:高电平用1表示,低电平用0表示
3.1 逻辑门电路的逻辑符号及外部特性 3.1.1 简单逻辑门电路 实现"与" 、 "或" 、 "非"三种基本运算的门电路 称为简单门电路。 F A B & (a) F A B 1 (b) F A 1 (c) 高电平:+5v 低电平:0v 正逻辑:高电平用1表示,低电平用0表示。 3.1.1

一、"与门 有两个或两个以上的输入端、一个输出端。 上图(a)的逻辑表达式为 F F=AB & 二、"或"门 有两个或两个以上的输入端,一个输出翳。 B 上图b)的逻辑表达式为 F=A+B ≥1 三、"非"门 A B 只有一个输入端,一个输出端。如 F 右图的逻辑表达式 -A 1 A
一、"与"门 有两个或两个以上的输入端、一个输出端。 上图(a)的逻辑表达式为 F=A B F A B & 二、" 或"门 有两个或两个以上的输入端,一个输出端。 上图(b)的逻辑表达式为 F=A +B F A B 1 三、" 非"门 只 有 一 个 输 入 端, 一个输出端。如 右图的逻辑表达式为 F = A A F 1

3.1.2复合逻辑门电路 复合门在逻辑功能上是简单逻辑门的组合, 实际性能上有所提高。常用的复合门有"与非" 门,"或非"门、"与或非"门和"异或"门等。 F A ≥1 & ≥1 & =1 A B A B AB CD A B (a) (b) (c) (d)
3.1.2 复合逻辑门电路 复合门在逻辑功能上是简单逻辑门的组合, 实际性能上有所提高。常用的复合门有"与非" 门,"或非"门、"与或非"门和"异或"门等。 F A B 1 (b) F A B & (a) F A 1 & B C D (c) F A =1 (d) B

一、"与非"门F=AB 使用"与非"门可以实现"与"、"或 & "、"非"3种基本运算,并可构成任何逻A B 辑电路,故称为通用逻辑门。 (a) F 二、"或非"门F=A+B ≥1 "或非"门也是一种通用门。 B (b)
二、"或非"门 F = A + B "或非"门也是一种通用门。 F A B 1 (b) 一、"与非"门 F = AB 使用"与非"门可以实现"与" 、 "或 " 、 "非"3种基本运算, 并可构成任何逻 辑电路, 故称为通用逻辑门。 F A B & (a)

F 三、"与或非"门F=AB+CD ≥1 & "与或非"门也是一种通用门。 四、"异或"门 (c) F “异或”运算是一种特殊的 逻辑运算,用符号①表示, =1 逻辑表达式为: B F=A⊕B=AB+AB (d) “同或”运算用符号⊙ 表示,逻辑表达式为: B F=A⊙B=AB+AB (e)
F A =1 (d) B F A =1 (e) B “同或”运算用符号 表示,逻辑表达式为: F = A B = AB + AB “异或”运算是一种特殊的 逻辑运算, 用符号表示, 逻辑表达式为: F = A B = AB + AB 四、"异或"门 三、"与或非"门 F = AB +CD "与或非"门也是一种通用门。 F A 1 & B C D (c)

3.2逻辑函数的实现 函数的表现形式和实际的逻辑电路之间有着对应 的关系,而实际逻辑电路大量使用“与非”门、“或非” “与1”用等“与非”门实现逻辑函数 第一步求出函数的最简“与一或”表达式。 第二步将其变换成“与非一与非”表达式。 第三步 画出函数表达式对应的逻辑电路图
3.2 逻辑函数的实现 函数的表现形式和实际的逻辑电路之间有着对应 的关系,而实际逻辑电路大量使用“与非”门、“或非”门、 “与或非”门等。 3.2.1 用“与非”门实现逻辑函数 第一步 求出函数的最简“与—或”表达式。 第二步 将其变换成“与非—与非”表达式。 第三步 画出函数表达式对应的逻辑电路图
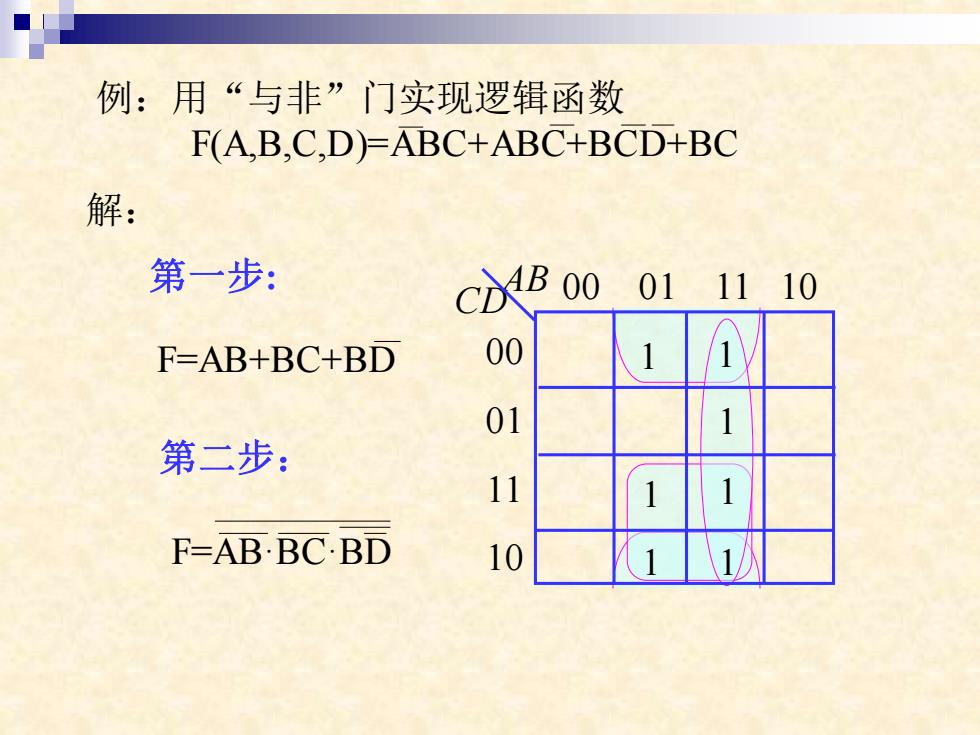
例:用“与非”门实现逻辑函数 F(A,B,C,D)=ABC+ABC+BCD+BC 解: 第一步: CDAB 00 011110 F-AB+BC+BD 00 1 01 1 第二步: 11 1 1 F=AB·BCBD 10 1 1
例:用“与非”门实现逻辑函数 F(A,B,C,D)=ABC+ABC+BCD+BC 解: 第一步: 00 01 11 10 00 01 11 10 AB CD 1 1 1 1 1 1 1 F=AB+BC+BD 第二步: F=AB·BC·BD