
第二节函数的求导法则一、四则运算求导法则二、反函数的求导法则三、复合函数求导法则四、初等函数的求导问题
第二节 二、反函数的求导法则 三、复合函数求导法则 四、初等函数的求导问题 一、四则运算求导法则 函数的求导法则

解决求导问题的思路:f(x+△x)- f(x)f'(x)= lim(构造性定义)△x△x-→0f[x+p(x)]-f(x)limp(Ax)-0p(Ax)
解决求导问题的思路: ( 构造性定义 ) ( ) 0 [ ( )] ( ) lim ( ) x f x x f x x

解决求导问题的思路:f(x+△x)- f(x)f'(x)= lim(构造性定义)△x△x-→0本节内容求导法则r(C)'=O(x")= uxu-l其他基本初等(sin x)'= cos x证明中利用了函数求导公式(ln x)'=两个重要极限X初等函数求导问题
解决求导问题的思路: ( 构造性定义 ) 求导法则 其他基本初等 函数求导公式 0 c o s x x 1 ( C ) ( s in x ) ( ln x ) 证明中利用了 两个重要极限 初等函数求导问题 本节内容 1 x ( ) x

一、四则运算求导法则定理1.函数u=(x)及v=v(x)都在点x可导u(x)及v(x)的和、差、积、商(除分母为0的点外)都在点x可导,且(1) [u(x)±v(x))'= u'(x)±v'(x)(2) [u(x)v(x))"= u'(x)v(x) +u(x)v'(x)u'(x)v(x)-u(x)v'(x)u(x)(v(x)± 0)(3)v(x)y?(x)
一、四则运算求导法则 定理1. 的和、差、积、商 (除分母 为 0的点外) 都在点 x 可导, 且 函 数 u u ( x ) 及 v v ( x ) 都 在 点 x 可 导 u ( x) 及 v( x) (1) [u ( x ) v ( x )] u ( x ) v ( x ) (2) [u ( x )v ( x )] u ( x )v ( x ) u ( x )v ( x ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (3) 2 v x u x v x u x v x v x u x ( v( x) 0 )

(l) (u±v)'=u'±y此法则可推广到任意有限项的情形.例如(u+v-w)'=u'+v'-w(2) (uv)'= u'y+ uv推论:1)(Cu)=Cu’(C为常数)2)(uvw)'=u'vw+u'w+uvwInx3)(logax)xlnana
此法则可推广到任意有限项的情形. (1 ) ( u v ) u v 例如, (u v w) u v w (2) ( u v ) u v u v 推论: 1) ( C u ) 2) ( uvw ) C u u vw uv w uvw 3) ( log a x ) a x ln ln x ln a 1 ( C为常数 )
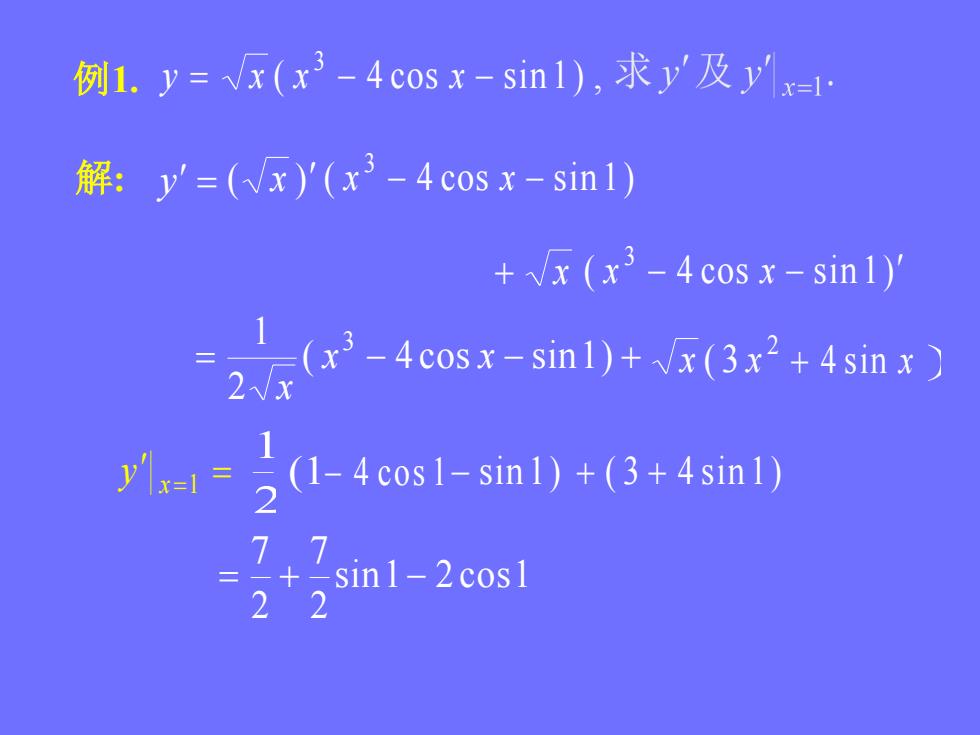
例1. = ~x(x3 - 4cos x-sin1),求y'及ylx=l解: y'=(Vx)'(x3 - 4cos x - sinl)+/x (x3 - 4cos x - sin1)-4cosx-sin1)+/x(3x+4sinx)(1-4cos1-sin1)+(3+4sin1)7Tsinl-2cosl2
例1. 解: 4 sin x ( 1 21 sin 1 ) ( 4 cos sin 1) , 3 y x x x y ( x ) x ( 4 cos sin1) 2 1 3 x x x 2 x ( 3 x ) y x 1 4 cos 1 ( 3 4 sin 1) sin1 2 cos1 27 27 ( 4 cos sin 1) 3 x x ( 4 cos sin 1) 3 x x
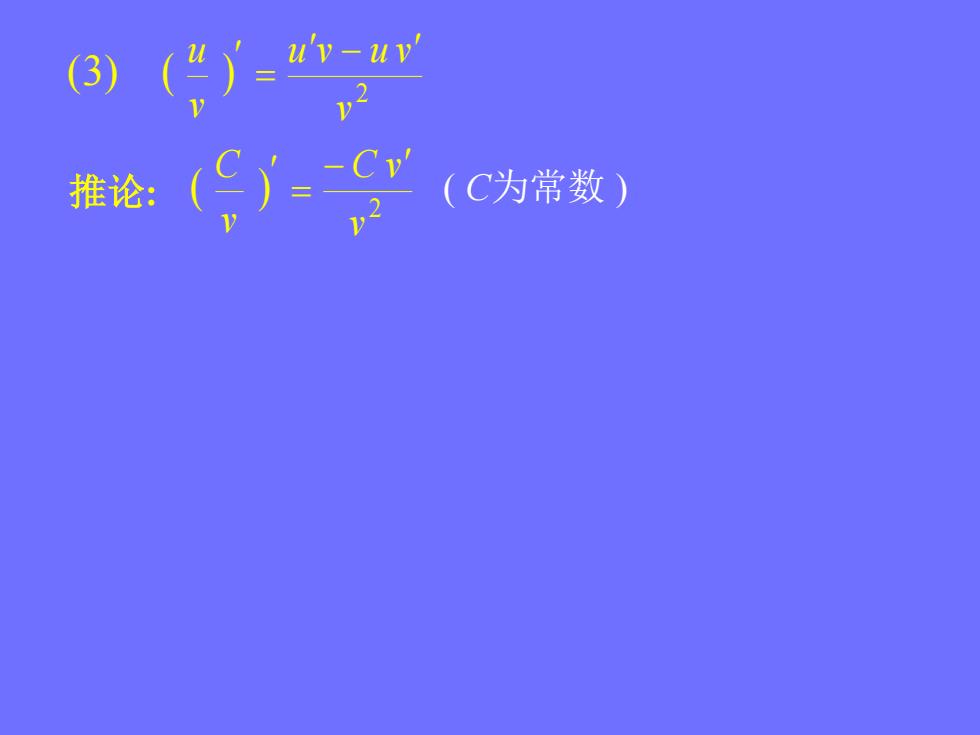
(3)(")_u-ur")_-Cv'(C为常数)推论:
(3) 2 v u v u v vu 推论 : 2 vC v vC ( C为常数 )

例2.求证(tan x)'= sec2 x, (cscx)=-csc xcot x.sinx(sinx)'cosx-sinx(cosx)证: (tanx)"cos? xcOSxcos? x +sin? x = sec?xcosx(sin x)- cos x(csc x)'=sinxsinxsinx=-cscxcotx类似可证:(cot x)'=- csc2x,(sec x)'= sec xtan x
(csc x) sin x 1 x 2 sin (sin x) x 2 sin 例2. 求证 证: x x x cos sin (tan ) x 2 cos (sin x) cos x sin x (cos x) x 2 cos x 2 cos x 2 sin x 2 sec c o s x c sc x c o t x 类似可证: (cot ) csc , 2 x x (sec x ) sec x tan x

熟练掌握三角函数的导数:(sin x)' = cos x,(cos x)= -sin x,(tan x)'= sec? x,(cot x)' = - csc x (sec x)'= sec x tan x, (csc x)'=-csc x cot x
(cos ) sin , x x (sec ) sec tan , x x x 熟练掌握三角函数的导数: 2 (cot ) csc , x x

二、反函数的求导法则定理2. 设 y= f(x)为 x= f-l(y)的反函数,f-l(y)在y的某邻域内单调可导,且[f-(y)}"0dy11或f'(x)=dx[f-'(y)]'dxdy证:在x处给增量△x±0由反函数的单调性知AyAy= f(x+△x)-f(x)±0, AxAxAy且由反函数的连续性知△x→0时必有y→0,因此1Ay1= limf'(x)= limAx[f-'(y)"Ax->0 AxAy-0Ay
f (x) 二、反函数的求导法则 定理2. y 的某邻域内单调可导, 证: 在 x 处给增量 由反函数的单调性知 且由反函数的连续性知 因此 ( ) ( ) , 设 y f x 为 x f 1 y 的反函数 f 1 ( y) 在 [ ( )] 0 1 且 f y d d x y 或 x 0 , y f ( x x ) f ( x ) 0 , x y y x x 0 时必有 y 0 , x y f x x 0 ( ) lim lim 0 y y x y x d d 1 [ ( )] 1 f y 1 1 [ ( )] 1 f y 1 1