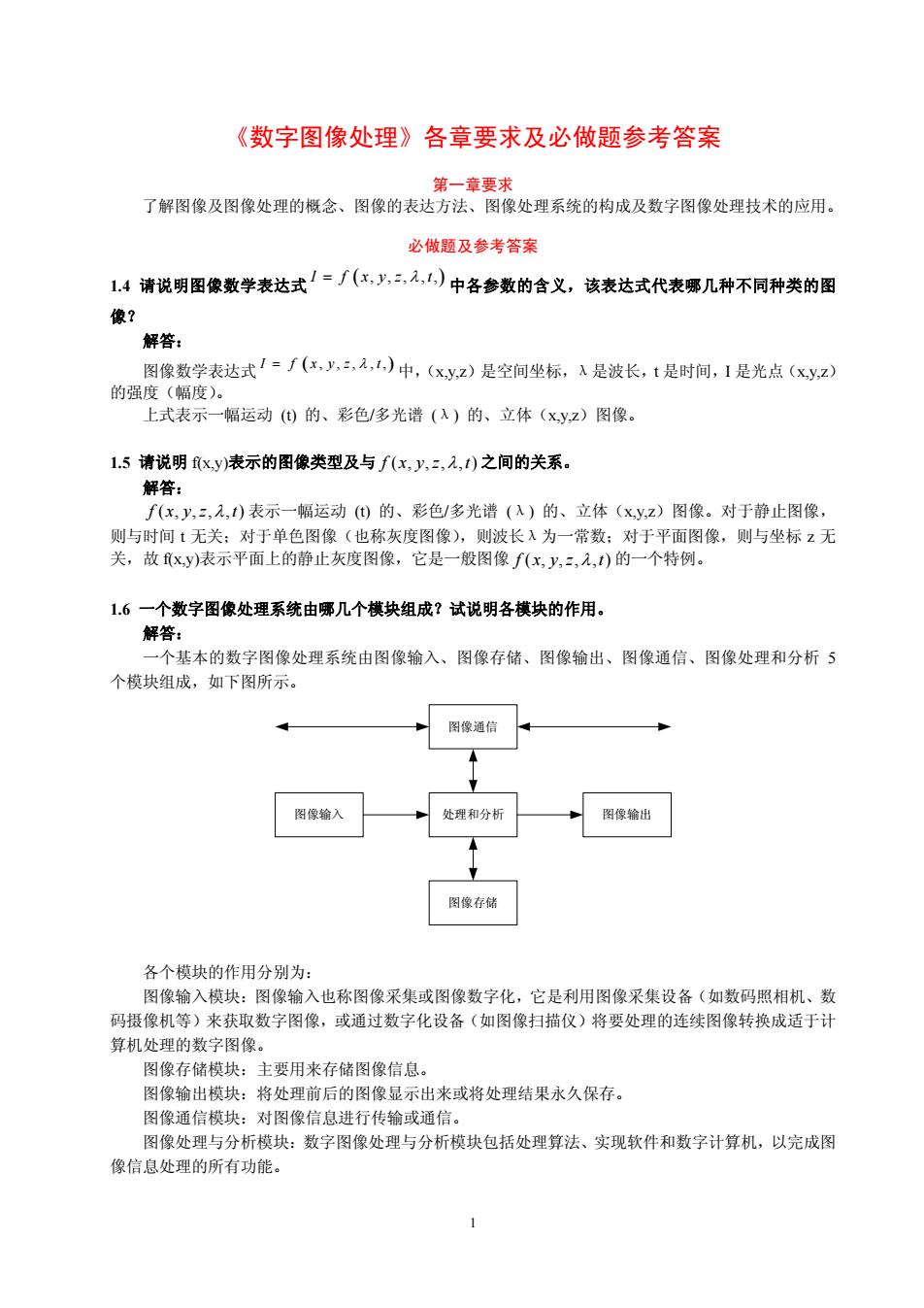
《数字图像处理》各章要求及必做题参考答案 解闲像及图像处理的概念、图像的表达方法·图豫处理系统的梢成及数字图像处理技术的应 必做题及参考答案 4请说明图像数学表达式(,,,)中各参数的含义,该表达式代表哪几种不同种类的图 像 解答: 图像数学表达式/=f(x,y,,,)中,(xy,z)是空间坐标,入是波长,t是时间,I是光点(xy,z》 的强度(幅度)。 上式表示一幅运动()的、彩色/多光谱(入)的、立体(xy2)图像。 1.5请说明xy表示的图像类型及与f(x,y,,,)之间的关系。 解答: f(x,y,:,,)表示一幅运动()的、彩色/多光谱(入)的、立体(xy,z)图像。对于静止图像, 则与时间t无关:对于单色图像(也称灰度图像),则波长入为一常数:对于平面图像,则与坐标z无 关,故y)表示平面上的静止灰度图像,它是一般图像fx,上,:,,)的一个特例。 1.6一个数字图像处理系统由哪几个模块组成?试说明各模块的作用。 解答: 一个基本的数字图像处理系统由图像输入、图像存储、图像输出、图像通信、图像处理和分析5 个模块组成,如下图所示 图像通信 图像输入 理和分析 图像缩出 图像存储 各个模块的作用分别为: 图像输入模块:图像输入也称图像采集或图像数字化,它是利用图像采集设备(如数码照相机、数 码摄像机等)来获取数字图像,或通过数字化设备(如图像扫描仪)将要处理的连续图像转换成适于计 算机处理的数字图像。 图像存储模块:主要用来存储图像信息。 图像输出模块:将处理前后的图像显示出来或将处理结果永久保存。 图像通信模块:对图像信息进行传输或通信, 图像处理与分析模块:数字图像处理与分析模块包括处理算法、实现软件和数字计算机,以完成图 像信息处理的所有功能。 1
1 《数字图像处理》各章要求及必做题参考答案 第一章要求 了解图像及图像处理的概念、图像的表达方法、图像处理系统的构成及数字图像处理技术的应用。 必做题及参考答案 1.4 请说明图像数学表达式 I = f xyz t ( ) , , , ,, λ 中各参数的含义,该表达式代表哪几种不同种类的图 像? 解答: 图像数学表达式 I = f xyz t ( ) , , , ,, λ 中,(x,y,z)是空间坐标,λ是波长,t 是时间,I 是光点(x,y,z) 的强度(幅度)。 上式表示一幅运动 (t) 的、彩色/多光谱 (λ) 的、立体(x,y,z)图像。 1.5 请说明 f(x,y)表示的图像类型及与 f (, , , ,) xyz t λ 之间的关系。 解答: f (, , , ,) xyz t λ 表示一幅运动 (t) 的、彩色/多光谱 (λ) 的、立体(x,y,z)图像。对于静止图像, 则与时间 t 无关;对于单色图像(也称灰度图像),则波长λ为一常数;对于平面图像,则与坐标 z 无 关,故 f(x,y)表示平面上的静止灰度图像,它是一般图像 f (, , , ,) xyz t λ 的一个特例。 1.6 一个数字图像处理系统由哪几个模块组成?试说明各模块的作用。 解答: 一个基本的数字图像处理系统由图像输入、图像存储、图像输出、图像通信、图像处理和分析 5 个模块组成,如下图所示。 图像通信 图像输入 处理和分析 图像输出 图像存储 各个模块的作用分别为: 图像输入模块:图像输入也称图像采集或图像数字化,它是利用图像采集设备(如数码照相机、数 码摄像机等)来获取数字图像,或通过数字化设备(如图像扫描仪)将要处理的连续图像转换成适于计 算机处理的数字图像。 图像存储模块:主要用来存储图像信息。 图像输出模块:将处理前后的图像显示出来或将处理结果永久保存。 图像通信模块:对图像信息进行传输或通信。 图像处理与分析模块:数字图像处理与分析模块包括处理算法、实现软件和数字计算机,以完成图 像信息处理的所有功能

第二章要求 1,了解三基色原理及颜色模型: 2.丁解人的视见将 必做题及参考答案 2.6人观察如题图2.6所示两幅形状相同的目标图像时,会觉得哪一个目标更亮一些?与实际亮度有无 不同?简述理由。[黑色(最暗)灰度值定为0,白色(最亮)灰度值定为25] y背景 60 日标 (a) (b) 题图2.6 解答: 两个不同亮度的目标物处于不同亮度的背景中,人会按对比度感觉目标物的亮度对比,因此人感觉 (a)要亮一些,但事实上,目标(b)的实际亮度要高于(a)的实际亮度。 2.7在串行通信中,常用波特率描述传输的速率 它被定义为每秒传输的数据比特数。串行通信中, 数据传输的单位是帧,也称字符。假如一帧数据由一个起始比特位、8个信息比特位和一个结束比 特位构成。根据以上概念,请问: (1)如果要利用一个波特率为56kbps(1k=1000)的信道来传输一幅大小为1024×1024、256 级灰度的数字图像需要多长时间? (2)如果是用波特率为750kbs的信道来传输上述图像,所需时间又是多少? (3)如果要传输的图像是512×512的真彩色图像(颜色数目是32b),则分别在上面两种信道 下传输,各需要多长时间? 解答: (1)传输的比特数为1024×1024×8×(1+8+1)/8=10485760,则在波特率为56kbps的信道上传 输时,所需时间为10485760/56000=187.25秒. (2)传输的比特数为1024×1024×8×(1+8+1)/8=10485760,则在波特率为750kbps的信道上 传输时,所需时间为10485760/750000=13.98秒。 (3)传输的比特数为512×512×32×(1+8+1)/8=10485760。在波特率为56khDs的信道上传输 时,所需时间为10485760/5600=187.25秒:在波特率为750kbps的信道上传输时,所需时间为 10485760/750000=13.98秒。 2.10(1) 存储 幅1024×768,256个灰度级的图像需要多少bit? (2) 一隔512×512的32bit真衫图像的容量为多少bit? 解答: (1)一幅1024×768,256个灰度级的图像的容量为:b=1024×768×8=6291456bit (2)一幅512×512的32位真彩图像的容量为:b=512×512×32=8388608bit
2 第二章要求 1. 了解三基色原理及颜色模型; 2. 了解人的视觉特性; 3. 了解图像数字化过程及分辨率变化对图像的影响; 4. 了解数字图像的表示形式和特点。 必做题及参考答案 2.6 人观察如题图 2.6 所示两幅形状相同的目标图像时,会觉得哪一个目标更亮一些?与实际亮度有无 不同?简述理由。[黑色(最暗)灰度值定为 0,白色(最亮)灰度值定为 255] 题图 2.6 解答: 两个不同亮度的目标物处于不同亮度的背景中,人会按对比度感觉目标物的亮度对比,因此人感觉 (a)要亮一些,但事实上,目标(b)的实际亮度要高于(a)的实际亮度。 2.7 在串行通信中,常用波特率描述传输的速率,它被定义为每秒传输的数据比特数。串行通信中, 数据传输的单位是帧,也称字符。假如一帧数据由一个起始比特位、8 个信息比特位和一个结束比 特位构成。根据以上概念,请问: (1)如果要利用一个波特率为 56kbps(1k=1000)的信道来传输一幅大小为1024 1024 × 、256 级灰度的数字图像需要多长时间? (2)如果是用波特率为 750kbps 的信道来传输上述图像,所需时间又是多少? (3)如果要传输的图像是512 512 × 的真彩色图像(颜色数目是 32 bit),则分别在上面两种信道 下传输,各需要多长时间? 解答: (1)传输的比特数为 1024×1024×8×(1+8+1)/8=10485760,则在波特率为 56kbps 的信道上传 输时,所需时间为 10485760/56000=187.25 秒。 (2)传输的比特数为 1024×1024×8×(1+8+1)/8=10485760,则在波特率为 750kbps 的信道上 传输时,所需时间为 10485760/750000=13.98 秒。 (3)传输的比特数为 512×512×32×(1+8+1)/8=10485760。在波特率为 56kbps 的信道上传输 时,所需时间为 10485760/56000=187.25 秒;在波特率为 750kbps 的信道上传输时,所需时间为 10485760/750000=13.98 秒。 2.10(1) 存储一幅 1024×768,256 个灰度级的图像需要多少 bit? (2) 一幅 512×512 的 32 bit 真彩图像的容量为多少 bit? 解答: (1)一幅 1024×768,256 个灰度级的图像的容量为: b=1024 768 8 6291456 bit × × = (2)一幅 512×512 的 32 位真彩图像的容量为: b=512 512 32=8388608 bit × × 20 50 60 100 背景 目标 (a) (b)

2.1某一线性移不变系统,其点扩展函数h(x,y)是输入为(x)6(y)时系统的输出,求下述情况下的 调制转移函数H(u,Y)。 (1)hx,y)=6x-xo)6(y-%) 2)Mx)=5 ·Ixsa和yKb 其他 3)A(x,)=6,量花)eR 其中R如题图2.11所示。 题图2.11 解答: (1)H(u,v)=[h(x,y)e-me-r dxdy =6(x-x)(y-yo)e-me-m dxdy 6(x-xd(y-yoe dy =eme-m (2)H(u.v)(x.yee-mdidy Eedemdy =Be-em embenb -ju =4E Sinuasin vb n (3)H(4,)=∫∫h(x,y)eexdy dEee dydEee dy 2sin2sinv(a sn2sinr(x+a d V =S[C(e-e)e+oa] _4jE(usin va-vsinua) v(u2-p2) 3
3 2.11 某一线性移不变系统,其点扩展函数 hxy (, ) 是输入为 δ ()() x δ y 时系统的输出,求下述情况下的 调制转移函数 H (,) u v 。 (1) 0 0 hxy x x y y (, ) ( )( ) =− − δ δ (2) || || (, ) {0 E xa yb hxy ≤ ≤ = , 和 , 其他 (3) (, ) (, ) { 0 E xy R hxy ∈ = , ,其他 其中 R 如题图 2.11 所示。 解答: (1) (,) (, ) jux jvy H u v h x y e e dxdy +∞ +∞ − − −∞ −∞ = ∫ ∫ 0 0 ( )( ) jux jvy δ δ x x y y e e dxdy +∞ +∞ − − −∞ −∞ = −− ∫ ∫ 0 0 () ( ) jux jvy δ δ x x e dx y y e dy +∞ +∞ − − −∞ −∞ =− − ∫ ∫ 0 0 jux jvy e e − − = (2) (,) (, ) a b jux jvy a b H u v h x y e e dxdy + + − − − − = ∫ ∫ a b jux jvy a b E e dx e dy + + − − − − = ∫ ∫ jua jua jvb jvb e ee e E ju jv − − − − = − − sin sin 4 ua vb E uv = (3) (,) (, ) jux jvy H u v h x y e e dxdy +∞ +∞ − − −∞ −∞ = ∫ ∫ 0 0 xa a xa jux jvy jux jvy a xa xa dx Ee e dy dx Ee e dy + −+ −− −− − −− − = + ∫ ∫ ∫∫ 0 0 2sin ( ) 2sin ( ) a jux jux a vx a v x a E e dx E e dx v v − − − + − + = + ∫ ∫ 0 0 2sin ( ) 2sin ( ) jux jux a a vx a vx a E e dx E e dx v v − − − + + = − ∫ ∫ ( ) ( ) ( ) 0 0 2 2 2 sin ( ) 4 sin sin ( ) 4 sin sin jux jux a a E e e v x a dx v jE ux v x a dx v jE u va v ua vu v − − − ⎡ ⎤ = −+ ⎢ ⎥ ⎣ ⎦ − ⎡ ⎤ = + ⎢ ⎥ ⎣ ⎦ − = − ∫ ∫

第三章要求 1.了解图像的儿何变换: 解图像的离散立叶变换,掌握其重要性质 掌图像的高散沃年 6.了解KL变换的原理。 必做题及参考答案 3.3证明f(x)的自相关函数的傅立叶变换就是f(x)的功率谱(谱密度)F(u)。 证明: 根据相关定理 f(x)of(x)台F(u)F(u) 另根据共轭定义 F(u)F(u)=F(u)F(u) 又根据共轭对称性F(u)=F(w)×F(u 即可证明f(x)的自相关函数的傅立叶变换就是f(x)的功率谱(谱密度)F(u)。 34已知NXN的数字图像为f血,n),其DFT为F(仙,),求-1)f(,的DFT 解答: 令4=g=,f(m,m))F(u,) 则(-1)"fm,)F(u-,v-) 3.10求下列数字图像块的二维DHT. 「144 「441 「4444 1441 4411 444 f(m,m)= 1441 (2)5(m,n)= 441 (3)6(m,m 4 44 4 1441 4411 4444 解答: 由H= [11111 1-1-11 [1000-6 10060 则F=H4H= 0000 同理得F=H,∫,H= 0000 0000 0000 0000 0000 「16000] F=HH= 0000 0000 L0000
4 第三章要求 1. 了解图像的几何变换; 2. 了解图像的离散傅立叶变换,掌握其重要性质; 3. 了解变换的一般表示形式; 4. 了解图像的离散余弦变换的原理 ; 5. 掌握图像的离散沃尔什-哈达玛变换; 6. 了解 K-L 变换的原理。 必做题及参考答案 3.3 证明 f ( ) x 的自相关函数的傅立叶变换就是 f ( ) x 的功率谱(谱密度) 2 F u( ) 。 证明: 根据相关定理 * f () () () () x f x F uFu o ⇔ 另根据共轭定义 * F () () () () uFu FuFu = 又根据共轭对称性 2 Fu Fu Fu () () () = × 即可证明 f ( ) x 的自相关函数的傅立叶变换就是 f ( ) x 的功率谱(谱密度) 2 F u( ) 。 3.4 已知 N×N 的数字图像为 f(m,n),其 DFT 为 F(u,v),求(-1)m+nf(m,n)的 DFT。 解答: 令 0 0 2 N u v = = , f (,) , mn F uv ↔ ( ) 则( ) ( ) 2 2 1 (,) , m n N N f mn F u v + − ↔ −− 3.10 求下列数字图像块的二维 DHT。 123 14 41 4 411 4 4 4 4 14 41 4 411 4 4 4 4 (1) ( , ) , (2) ( , ) , (3) ( , ) 14 41 4 411 4 4 4 4 14 41 4 411 4 4 4 4 f mn f mn f mn ⎡⎤ ⎡⎤ ⎡ ⎤ ⎢⎥ ⎢⎥ ⎢ ⎥ === ⎣⎦ ⎣⎦ ⎣ ⎦ 解答: N N 2 2 N N 4 1 1 1 1 H H 2 2 1 -1 H -H 11 1 1 1 1 -1 1 -1 H 2 1 1 -1 -1 1 -1 -1 1 H H N ⎡ ⎤ ⎡ ⎤ = = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 由和 得 则 1 41 4 10 0 0 6 0 00 0 0 00 0 0 00 0 F H fH ⎡ ⎤ − ⎢ ⎥ = = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 同理得 2 42 4 10 0 6 0 0 000 0 000 0 000 F H fH ⎡ ⎤ ⎢ ⎥ = = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 3 43 4 16 0 0 0 0 000 0 000 0 000 F H fH ⎡ ⎤ ⎢ ⎥ = = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦

3.11求习题3.10的二维DwT 解答: 由H,→W,得 11117 11 「100-601 「106001 0000 0000 则E=WfW= 000 E=形形=0000 000 0 0000 [16000] 0000 F=WfW= 0000 0000 3.16设有3个矢量x,=100,x:=110,x,=10',请求出矢量 X=[x,XX,了的协方差矩阵Cx。 解答: C=立2-mm得 「11 「31 C=o[0,o+11+o0,小-13,1, L1 =110 311 019311012
5 3.11 求习题 3.10 的二维 DWT。 解答: 4 4 4 11 1 1 1 1 1 -1 -1 2 1 -1 -1 1 1 -1 1 -1 H W W → ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 由 ,得 则 1 41 4 10 0 6 0 0000 0000 0000 F W fW ⎡ ⎤ − ⎢ ⎥ = = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 2 42 4 10 6 0 0 0 000 0 000 0 000 F W fW ⎡ ⎤ ⎢ ⎥ = = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 3 43 4 16 0 0 0 0 000 0 000 0 000 F W fW ⎡ ⎤ ⎢ ⎥ = = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 3.16 设有 3 个矢量 1 [100] T x = , 2 [110] T x = , 3 [101] T x = ,请求出矢量 3 1 2 T = ⎡ ⎤ ⎣ ⎦ Xxxx 的协方差矩阵CX 。 解答: 根据式 1 1 M x M k k m x = = ∑ 得 1 1 3 3 111 3 010 1 001 1 mX ⎧ ⎫ ⎡⎤ ⎡⎤ ⎡⎤ ⎡⎤ ⎪ ⎪ ⎢⎥ ⎢⎥ ⎢⎥ ⎢⎥ = ++ = ⎨ ⎬ ⎪ ⎪ ⎩ ⎭ ⎣⎦ ⎣⎦ ⎣⎦ ⎣⎦ 1 1 M T T x M kk x x k C xx mm = = − ∑ 得 [ ] [ ] [ ] [ ] 1 113 1 1 1 11 0 1,0,0 1 1,1,0 0 1,0,1 1 3,1,1 3 3 3 33 0 011 311 9 33 0 0 0 11 1 110 311 0 2 1 39 9 101 311 0 12 Cx ⎡⎤ ⎡⎤ ⎡⎤ ⎡⎤ ⎢⎥ ⎢⎥ ⎢⎥ ⎢⎥ = ++− ⎣⎦ ⎣⎦ ⎣⎦ ⎣⎦ ⎡ ⎤⎡ ⎤ ⎡ ⎤ ⎢ ⎥⎢ ⎥ ⎢ ⎥ = − =− ⎣ ⎦⎣ ⎦ ⎣ ⎦ −
第四章要求 1.掌握图像的灰度变换、直方图修正、空域及频域平滑与锐化方法: 平均滤波法的异同: 必做题及参考答案 4.4设1幅图像具有如题表4.4.1所示概率分布,对其分别进行直方图均衡化和规定化。要求规定化后 的图像具有如题表4.42所示的灰度级分布。 题表44.1 灰度级 01 234567 各灰度级概率分布0.140.220.250.170.100.060.030.03 题表4.4.2 灰度级 01 234567 各灰度级概率分布0000.190.250.210.240.11 解答 (1)直方图均衡化结果如下表所示 号 运算 步骤和结果 列出原图像灰度级了 01234567 各灰度级概帝分布(直方图)P 0.14 022 0.250.17 0,10 0.06 0.03 0.03 计算计直方图P,名P 0.14 0.36 0.610.78 0.88 0.94 0.97 1.00 4 计算变后的府值。 3 6 > 1=INTI(L-D)P +0.51 确定映射对应关系→j) 0→11→324354-6 5.6.7+7 计算新直方图P( 00.1400.220.250.170.100.12 (2)直方图规定化结果如下表所示。 序 步骤和结果 县 运算 列出图像灰度级(或j) 01234567 2 原图像各灰度级概分布P00.140.220.250.170.100.060.030.03 3 计算原图像累计直方图P 0.140360.610.780.880.940.971.00 4 规定直方图P) 0000.190250.210.240.11 计算规定累计直方图 0000.190.440.650.891.00 6 按照P→P找到i对应的j 34 5 66 77 7 7 确定变换关系1→于 0-31-42-53.4-6 5.6.7→7 8求变换后的匹配直方图P0)0000.140,220.250.270.12 6
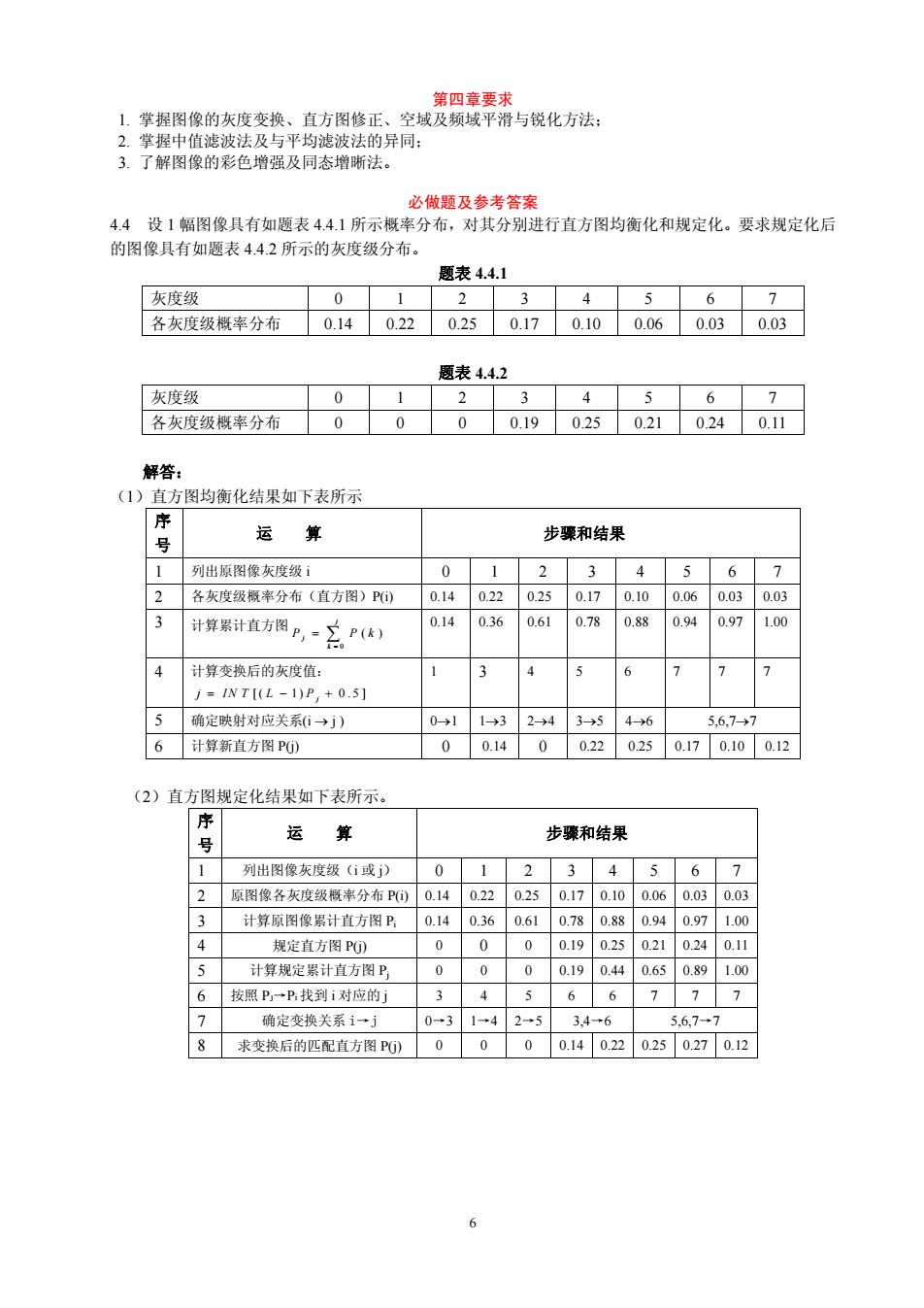
6 第四章要求 1. 掌握图像的灰度变换、直方图修正、空域及频域平滑与锐化方法; 2. 掌握中值滤波法及与平均滤波法的异同; 3. 了解图像的彩色增强及同态增晰法。 必做题及参考答案 4.4 设 1 幅图像具有如题表 4.4.1 所示概率分布,对其分别进行直方图均衡化和规定化。要求规定化后 的图像具有如题表 4.4.2 所示的灰度级分布。 题表 4.4.1 灰度级 0 1 2 3 4 5 6 7 各灰度级概率分布 0.14 0.22 0.25 0.17 0.10 0.06 0.03 0.03 题表 4.4.2 灰度级 0 1 2 3 4 5 6 7 各灰度级概率分布 0 0 0 0.19 0.25 0.21 0.24 0.11 解答: (1)直方图均衡化结果如下表所示 序 号 运 算 步骤和结果 1 列出原图像灰度级 i 0 1 2 3 4 5 6 7 2 各灰度级概率分布(直方图)P(i) 0.14 0.22 0.25 0.17 0.10 0.06 0.03 0.03 3 计算累计直方图 0 ( ) j j k P P k = = ∑ 0.14 0.36 0.61 0.78 0.88 0.94 0.97 1.00 4 计算变换后的灰度值: [( 1) 0.5] j j IN T L P = −+ 1 3 4 5 6 7 7 7 5 确定映射对应关系(i → j ) 0→1 1→3 2→4 3→5 4→6 5,6,7→7 6 计算新直方图 P(j) 0 0.14 0 0.22 0.25 0.17 0.10 0.12 (2)直方图规定化结果如下表所示。 序 号 运 算 步骤和结果 1 列出图像灰度级(i 或 j) 0 1 2 3 4 5 6 7 2 原图像各灰度级概率分布 P(i) 0.14 0.22 0.25 0.17 0.10 0.06 0.03 0.03 3 计算原图像累计直方图 Pi 0.14 0.36 0.61 0.78 0.88 0.94 0.97 1.00 4 规定直方图 P(j) 0 0 0 0.19 0.25 0.21 0.24 0.11 5 计算规定累计直方图 Pj 0 0 0 0.19 0.44 0.65 0.89 1.00 6 按照 Pj→Pi 找到 i 对应的 j 3 4 5 6 6 7 7 7 7 确定变换关系 i→j 0→3 1→4 2→5 3,4→6 5,6,7→7 8 求变换后的匹配直方图 P(j) 0 0 0 0.14 0.22 0.25 0.27 0.12

4.5设工业检测中工件的图像受到零均值、与图像不相关噪声的影响。假设图像采集装置每秒可采集30 幅图,若采用图像平均法将噪声的均方差减小到原来的110,则工件需固定在采集装置前多长时间? 解答: 由式(4.3.19)可知通过图像平均法可以将噪声均方差降低到原来的√,M为用于平均的图像个 数,所以如果 0g=ton=√Fo 解得,M=100 =100/30=3.33秒 4.8对于如下所示的空域增强公式,试推导出其相应的频域等价滤波器H(u,)。 g(m,n)=f(m,n)-f(m+ln)+f(m,n)-f(m,n+l) 解答: 对题设表达式进行傅立叶变换得 G(u,v)=F(u,v)-F(u,v)e+F(u,v)-F(u,v)e =[1-e2/wTF(u,p)+[1-e2nw1F(u,) =【1-e2a)+(1-e2a]F(u,v) =H(u.v)F(u.v) 所以,频域的等价滤波器为 H(u,v)=(1-e2)+(1-e2m)】 4.16如题图4.16所示256×256的二值图像(白为1,黑为0),其中的白条是7像素宽,210像素高 两个白条之间的宽度是17像素,当应用下面的方法处理时图像的变化结果(按最靠近原)仍取0或I) 是什么?(图像边界不考虑) (1)3×3的邻域平均滤波 (2)7×7的邻域平均滤波。 (3)9×9的邻域平均滤波 题图4.16
7 4.5 设工业检测中工件的图像受到零均值、与图像不相关噪声的影响。假设图像采集装置每秒可采集 30 幅图,若采用图像平均法将噪声的均方差减小到原来的 1/10,则工件需固定在采集装置前多长时间? 解答: 由式(4.3.19)可知通过图像平均法可以将噪声均方差降低到原来的 1 M ,M 为用于平均的图像个 数,所以如果 1 1 σ g 10σ σ n n M = = 解得,M=100 t=100/30=3.33 秒 4.8 对于如下所示的空域增强公式,试推导出其相应的频域等价滤波器 Huv (,) 。 gmn f mn f m n f mn f mn ( , ) ( , ) ( 1, ) ( , ) ( , 1) = − ++ − + 解答: 对题设表达式进行傅立叶变换得 2/ 2/ 2/ 2/ 2/ 2/ (,) (,) (,) (,) (,) 1 (,) 1 (,) [(1 ) (1 )] ( , ) (,) (,) j uM j vN j uM j vN j uM j vN Guv Fuv Fuve Fuv Fuve e Fuv e Fuv e e Fuv HuvFuv π π π π π π =− +− =− +− ⎡ ⎤⎡⎤ ⎣ ⎦⎣⎦ = − +− = 所以,频域的等价滤波器为 2/ 2/ ( , ) (1 ) (1 ) j uM j vN Huv e e π π =− +− 4.16 如题图 4.16 所示256 256 × 的二值图像(白为 1,黑为 0),其中的白条是 7 像素宽,210 像素高。 两个白条之间的宽度是 17 像素,当应用下面的方法处理时图像的变化结果(按最靠近原则仍取 0 或 1) 是什么?(图像边界不考虑) (1)3 3 × 的邻域平均滤波。 (2)7 7 × 的邻域平均滤波。 (3)9 9 × 的邻域平均滤波。 题图 4.16

解答: 在题图4.16中,由于取值为1的白条的宽度是7,大于9×9滤波窗宽的一半(4.5),当然也大于7×7 和3×3的窗宽的一半。这样就使得在用这三种邻域平均滤波时,若滤波像素点的值是1,则滤波窗中1 的个数必多 于窗内参加平均的像素个数的一半 平均并四舍五入后的结果仍为1:同理 ,若滤波像素点 的值是0,则滤波窗中0的个数必多于窗内参加平均的像素个数的一半,平均并四舍五入后的结果仍为 0。所以,按题意对题图4.16所示二值图像用三种大小不同的邻域进行邻域平均滤波时,结果图像与原 图像相同。 4.17用中值滤波重复习题4.16的问题。 解答: 与题4.16的道理类似。在题图4.16中,由于取值为1的白条的宽度是7,大于9×9滤波窗宽的一 半(4.5),当然也大于7×7和3×3的窗宽的一半。这样就使得在用这三种大小的滤波窗进行中值滤波 时,若滤波像素点的值是1(或0),则滤波窗中1(或0)的个数必多于窗内0(或1)的个数,则排在 中间的值仍为1(或0)不变,即中值滤波后,图像没有变化 4.18如题图4.18所示两幅图像(白为1,黑为0)完全不同,但它们的直方图是相同的。假设每幅图像 均用3×3的平滑模板进行处理(图像边界不考虑,结果按四含五入仍取0或1)。 (1)处理后的图像的直方图还是一样么? (2)如果不一样,则求出这两个直方图。 题图4.18(图像大小为64×64像素) 解答 当采用3×3的平滑模板(4邻或8邻平均,4邻或8邻 1(或0),则滤波☒中1 (或0)的个数必 多于窗内0(或】)的个数,则平滑后的值仍为1(或0)不变,即用3×3的平滑模板处理后,图像没 有变化。因此,直方图也没有变化。 (2)对于题图418(右)所示二值方块图像,当采用3×3的4邻或8邻加权平均平滑模板或中值 滤波进行处理时,若滤波像素点的值是】(或0 ,则滤波窗中1(或0)的个数必多于窗内0(或1)的 个数,则平滑后的值仍为1(或0)不变,即图像没有变化。因此,直方图也没有变化 当采用3×3的4邻或8邻平均平滑模板(见图4.18.1)处理时,当处理点位于白、黑块组成的4 块交界处(图4.18.2(左)中心的4个阴影像素)时,若滤波像素点的值是1或0时,则滤波窗中参加 平均的1的个数等于0的个数,则平均并四舍五入时,结果都为1,见图4.182(右)中心的4个阴影 像素).此时,整个图像处理后的结果见图4.183所示,图像的直方图由P)=(PO),P(1)}={号,;变 成了P0)=P0),P1}={2-,49}={0.48,0.52,其余情况下,平滑结果不变,当然直方 图也不改变
8 解答: 在题图 4.16 中,由于取值为 1 的白条的宽度是 7,大于9 9 × 滤波窗宽的一半(4.5),当然也大于7 7 × 和3 3 × 的窗宽的一半。这样就使得在用这三种邻域平均滤波时,若滤波像素点的值是 1,则滤波窗中 1 的个数必多于窗内参加平均的像素个数的一半,平均并四舍五入后的结果仍为 1;同理,若滤波像素点 的值是 0,则滤波窗中 0 的个数必多于窗内参加平均的像素个数的一半,平均并四舍五入后的结果仍为 0。所以,按题意对题图 4.16 所示二值图像用三种大小不同的邻域进行邻域平均滤波时,结果图像与原 图像相同。 4.17 用中值滤波重复习题 4.16 的问题。 解答: 与题 4.16 的道理类似。在题图 4.16 中,由于取值为 1 的白条的宽度是 7,大于9 9 × 滤波窗宽的一 半(4.5),当然也大于7 7 × 和3 3 × 的窗宽的一半。这样就使得在用这三种大小的滤波窗进行中值滤波 时,若滤波像素点的值是 1(或 0),则滤波窗中 1(或 0)的个数必多于窗内 0(或 1)的个数,则排在 中间的值仍为 1(或 0)不变,即中值滤波后,图像没有变化。 4.18 如题图 4.18 所示两幅图像(白为 1,黑为 0)完全不同,但它们的直方图是相同的。假设每幅图像 均用3 3 × 的平滑模板进行处理(图像边界不考虑,结果按四舍五入仍取 0 或 1)。 (1)处理后的图像的直方图还是一样么? (2)如果不一样,则求出这两个直方图。 题图 4.18 (图像大小为 64×64 像素) 解答: (1)对于题图 4.18(左)所示二值图像,当采用3 3 × 的平滑模板(4 邻或 8 邻平均,4 邻或 8 邻 加权平均,或中值滤波)进行处理时,若滤波像素点的值是 1(或 0),则滤波窗中 1(或 0)的个数必 多于窗内 0(或 1)的个数,则平滑后的值仍为 1(或 0)不变,即用3 3 × 的平滑模板处理后,图像没 有变化。因此,直方图也没有变化。 (2)对于题图 4.18(右)所示二值方块图像,当采用3 3 × 的 4 邻或 8 邻加权平均平滑模板或中值 滤波进行处理时,若滤波像素点的值是 1(或 0),则滤波窗中 1(或 0)的个数必多于窗内 0(或 1)的 个数,则平滑后的值仍为 1(或 0)不变,即图像没有变化。因此,直方图也没有变化。 当采用3 3 × 的 4 邻或 8 邻平均平滑模板(见图 4.18.1)处理时,当处理点位于白、黑块组成的 4 块交界处(图 4.18.2(左)中心的 4 个阴影像素)时,若滤波像素点的值是 1 或 0 时,则滤波窗中参加 平均的 1 的个数等于 0 的个数,则平均并四舍五入时,结果都为 1,见图 4.18.2(右)中心的 4 个阴影 像素)。此时,整个图像处理后的结果见图 4.18.3 所示,图像的直方图由 P(i)={P(0) , P(1)}={ 1 1 2 2 , }变 成了 P(i)={P(0) , P(1)}={ 2048 98 2048 98 64 64 64 64 , − + × × }= { 0.48 , 0.52},其余情况下,平滑结果不变,当然直方 图也不改变

010 111 w=101 010 111 图4.18.14邻域平均和8邻域平均模板 11110000 11110000 11110000 11 11 11 0 000 111 0 11110000 11111000 00001111 00011111 00001111 00001111 00001110 00001111 00001111 00001111 图4.182白、黑块组成的4块交界处 图4.18.34邻和8-邻平均模板处理后的结果图像 第五章要求 象复用的及过程 有原原理 离散退化模型和频域退化
9 1 1 4 010 101 010 ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ W , 1 2 8 111 101 111 ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ W 图 4.18.1 4-邻域平均和 8-邻域平均模板 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 图 4.18.2 白、黑块组成的 4 块交界处 图 4.18.3 4-邻和 8-邻平均模板处理后的结果图像 第五章要求 1. 了解图象恢复目的及过程; 2. 掌握各种形式的退化模型(离散退化模型和频域退化模型); 3. 了解无约束复原原理,掌握反向滤波法公式及使用时的注意事项; 4. 了解维纳和约束最小平方滤波法原理,掌握其结果讨论。 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 111 1 1 0 0 0 000 1 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1

第六章要求 1,掌握图像的数据沉余、编码模型、无损压缩编码: 2阶的最优预测器的设计 了解图 题 必做题及参考答案 6.2某视频图像为每秒30帧,每帧大小为512x512,32位真彩色。现有40GB的可用硬盘空间,可以 存储多少秒的该视频图像?若采用隔行扫描且压缩比为10的压缩方法,又能存储多少秒的该视频 图像? 解答 (1)40GB的硬盘可以存储该视烦图像 40×20×8 12×512×32×30136533 (2)采用隔行扫描且压缩比为10的压缩方法,40GB的硬盘可以存储该视频图像 40×20x8 512×512×32×30×号×奇*27306.675 6.6已知符号A、B、C出现的概率分别为0.4、02和0.4,请对符号串BACCA进行算术编码,写出 编码过程,求出信息的熵、平均码长和编码效率 解答: 首先确定信源符号,概率和初始编码间隔: 符号 A 04 02 04 初始编码间隔 0.0.4) [0.40.6) 0.6,1 编码过程: 步骤输入符号编码间隔 编码判定 [0.4,0.6 符号间隔0.4,0.6) 2 A 0.4.0.48) 「0.4.0.6)间隔的0一40% 0448048) 04048)1图的60一100% [0.4672.0.48) [0.448,0.48)间隔的60-100% 5 0.4672,0.47232 0.4672,0.48)间隔的0-40% 70.4672.0.47232)中选择一个数0.46875作为输出 对BACCA进行编码: 第一个编码符号为“B”,其初始区间为[,h)=[0.4,0.6),则“当前区间”[L(),H()为 [L(I)=L(O)+R(O)×1 H()=L(O)+R(O)×h 其中「L(0),H(O)=[0,1)则R(0)=H(0)-L(O)=1-0=1 ,L(0=0+1×0.4 1H(①)=0+1×0.6 第二个编码符号为“A”,则其[1,hM)=[0,0.4),R(①)=H()-L(1)=0.6-0.4=0.2 10
10 第六章要求 1. 掌握图像的数据冗余、编码模型、无损压缩编码; 2. 掌握预测编码原理及大于或等于 2 阶的最优预测器的设计; 3. 了解图像压缩的原因与方法分类、保真度准则及正交变换编码原理; 4. 了解小波变换在图像压缩编码中的应用、小波变换编码的基本思想与特点及编码中需要解决的问 题。 必做题及参考答案 6.2 某视频图像为每秒 30 帧,每帧大小为 512×512,32 位真彩色。现有 40 GB 的可用硬盘空间,可以 存储多少秒的该视频图像?若采用隔行扫描且压缩比为 10 的压缩方法,又能存储多少秒的该视频 图像? 解答: (1)40 GB 的硬盘可以存储该视频图像 30 40 2 8 1365.33 512 512 32 30 s × × ≈ × ×× (2)采用隔行扫描且压缩比为 10 的压缩方法,40 GB 的硬盘可以存储该视频图像 30 1 1 2 10 40 2 8 27306.67 512 512 32 30 s × × ≈ × × × ×× 6.6 已知符号 A、B、C 出现的概率分别为 0.4、0.2 和 0.4,请对符号串 BACCA 进行算术编码,写出 编码过程,求出信息的熵、平均码长和编码效率。 解答: 首先确定信源符号,概率和初始编码间隔: 符号 A B C 概率 0.4 0.2 0.4 初始编码间隔 [0,0.4) [0.4,0.6) [0.6,1) 编码过程: 步骤 输入符号 编码间隔 编码判定 1 B [0.4,0.6) 符号间隔[0.4,0.6) 2 A [0.4,0.48) [0.4,0.6)间隔的 0-40% 3 C [0.448,0.48) [0.4,0.48)间隔的 60-100% 4 C [0.4672,0.48) [0.448,0.48)间隔的 60-100% 5 A [0.4672,0.47232) [0.4672,0.48)间隔的 0-40% 7 [0.4672,0.47232)中选择一个数 0.46875 作为输出 对 BACCA 进行编码: 第一个编码符号为“B”,其初始区间为[l h, 0.4,0.6 ) = [ ) ,则“当前区间” ⎡L H () () 1, 1 ) ⎣ 为: () ( ) ( ) () ( ) ( ) 100 100 LL Rl H L Rh ⎧⎪ =+× ⎨ ⎪ =+× ⎩ 其中 ⎡L H () () 0 , 0 0,1 ) = [ ) ⎣ 则 RHL (0 0 0 101 ) = ( ) − =− = ( ) ( ) ( ) 1 0 1 0.4 1 0 1 0.6 L H ⎧⎪ = +× ∴⎨ ⎪ = +× ⎩ 第二个编码符号为“A”,则其[l h, 0,0.4 ) = [ ) , RHL (1 1 1 0.6 0.4 0.2 ) = − =−= ( ) ( )