
第五章 图象恢复 ◆5.0 概述 ◆5.1 退化模型 ◆5.2 常见退化模型及辨识方法 ◆5.3 图像的无约束恢复 ◆5.4 图像的有约束最小二乘恢复 ◆5.5 几何畸变图像的恢复 ◆5.6 超分辨率图像复原 Digital Image Processing
Digital Image Processing Digital Image Processing ◆5.0 概述 ◆5.1 退化模型 ◆5.2 常见退化模型及辨识方法 常见退化模型及辨识方法 ◆5.3 图像的无约束恢复 图像的无约束恢复 ◆5.4 图像的有约束最小二乘恢复 图像的有约束最小二乘恢复 ◆5. 5 5. 5 几何畸变图像的恢复 几何畸变图像的恢复 5.6 超分辨率图像复原 超分辨率图像复原 第五章 图象恢复

5.0概述 基本概念 降质举例:宇航、卫星、航空测鲶、遥感、天文学中所得照片,由于大气 淋流,光学系统的相差及摄像机与物体之间的相对运动等,会使图像降 质。 退化图像:由于各种原因,使得原清晰图像变模糊,或者原图像没有达到 应有的质量而形成的降质图像。 图像恢复(复原):使退化图像恢复本来面目。 图像恢复过程及其关键:根据图像降质过程的某些先验知识,建立“褪化 (降质)模型”,运用和退化相反的过程,将退化图像恢复。 图像恢复准则:要用某一客观标准来度量,则为某种准则下的最优估计。 Digital Image Processing
Digital Image Processing Digital Image Processing ◘基本概念 降质举例:宇航、卫星、航空测绘、遥感、天文学中所得照片,由于大气 湍流,光学系统的相差及摄像机与物体之间的相对运动等,会使图像降 质。 退化图像:由于各种原因,使得原清晰图像变模糊,或者原图像没有达到 应有的质量而形成的降质图像。 图像恢复(复原): 使退化图像恢复本来面目。 图像恢复过程及其关键:根据图像降质过程的某些先验知识,建立“退化 (降质)模型”,运用和退化相反的过程,将退化图像恢复。 图像恢复准则:要用某一客观标准来度量,则为某种准则下的最优估计。 5.0 概 述

5.0 概述 图像恢复与图像增强的异同点 相同点:图像增强与图像恢复都是改善给定图像的质量。 不同点: (1)图像恢复是利用退化过程的先验知识,来建立图像的退化棋型,再采 用与退化相反的过程来恢复图像,而图像增强一般无需对图像降质过程建立 模型。 (2)图像恢复是针对图像葚体,以改善图像的葚体质量。而图像增强是针 对图像的局部,以改善因像的局部特性,如图像的平滑和锐化。 (3)图像恢复主要是利用图像退化过程来恢复图像的本来面目,它是一个 客观过程,最终的结果必须要有一个客观的评价准则。而图像增强主要是用 各种技术来改善图像的视觉效果,以适应人的心理、生理鼎要,而不考虑处 理后图像是否与原图像相符,也就很少涉及统一的客观评价准则。 Digital Image Processing
Digital Image Processing Digital Image Processing ◘图像恢复与图像增强的异同点 图像恢复与图像增强的异同点 相同点:图像增强与图像恢复都是改善给定图像的质量。 不同点: (1)图像恢复是利用退化过程的先验知识,来建立图像的退化模型,再采 用与退化相反的过程来恢复图像,而图像增强一般无需对图像降质过程建立 模型。 (2)图像恢复是针对图像整体,以改善图像的整体质量。而图像增强是针 对图像的局部,以改善图像的局部特性,如图像的平滑和锐化。 (3)图像恢复主要是利用图像退化过程来恢复图像的本来面目,它是一个 客观过程,最终的结果必须要有一个客观的评价准则。而图像增强主要是用 各种技术来改善图像的视觉效果,以适应人的心理、生理需要,而不考虑处 理后图像是否与原图像相符,也就很少涉及统一的客观评价准则。 5.0 概述
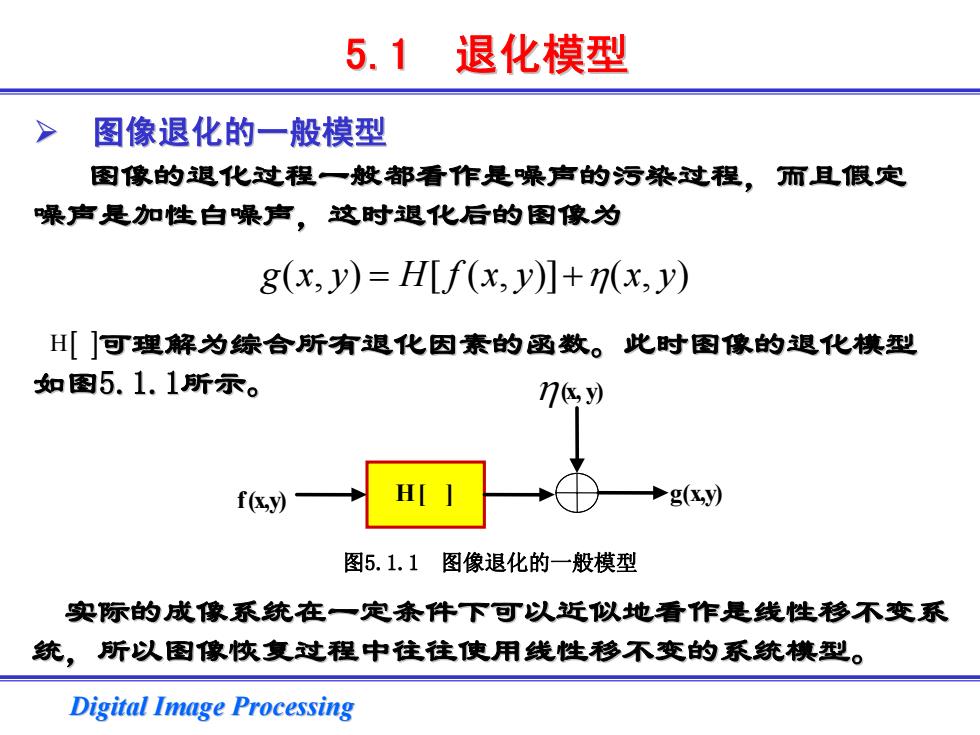
5.1 退化模型 图像退化的一般模型 图像的退化过程一般都看作是噪声的污染过程,而且假定 噪声是加性白噪声,这时退化后的图像为 8(x,y)=H[f(x,y)]+7(x,y) H[]可理解为综合所有退化因素的函数。此时图像的退化模型 如图5.1.1所示。 7飞) f(.y) 图5.1.1图像退化的一般模型 实际的成像系统在一定条件下可以近似地看作是线性移不变系 统,所以图像恢复过程中往往使用线性移不变的系统棋型。 Digital Image Processing
Digital Image Processing Digital Image Processing ¾ 图像退化的一般模型 图像退化的一般模型 图像的退化过程一般都看作是噪声的污染过程,而且假定 图像的退化过程一般都看作是噪声的污染过程,而且假定 噪声是加性白噪声,这时退化后的图像为 噪声是加性白噪声,这时退化后的图像为 可理解为综合所有退化因素的函数。此时图像的退化模型 可理解为综合所有退化因素的函数。此时图像的退化模型 如图5.1.1所示。 5.1 退化模型 g( , ) [ ( , )] ( , ) x y = H f x y +η x y H[ ] f (x,y) H[ ] (x, y) g (x,y) η 图5.1.1 图像退化的一般模型 实际的成像系统在一定条件下可以近似地看作是线性移不变系 实际的成像系统在一定条件下可以近似地看作是线性移不变系 统,所以图像恢复过程中往往使用线性移不变的系统模型。 统,所以图像恢复过程中往往使用线性移不变的系统模型

5.1 退化模型 离散退化模型 对图像及其点扩散函数进行均匀采样就可以得到离牧退化 模型,由于退化过程是卷积过程,线性卷积后点数变多,为 了方便计算,需要将各函数进行延拓,具体如下所示: f(m,n) 0≤m≤A-1且0≤n≤B-1 f.(m.n)=0 A≤m≤M-1或B≤n≤N-1 A=” 0≤m≤C-1且0≤n≤D-1 C≤m≤M-1或D≤n≤N-1 0≤m≤A-1且0≤n≤B-1 A≤m≤M-1或B≤n≤N-1 Digital Image Processing
Digital Image Processing Digital Image Processing 离散退化模型 对图像及其点扩散函数进行均匀采样就可以得到离散退化 对图像及其点扩散函数进行均匀采样就可以得到离散退化 模型,由于退化过程是卷积过程,线性卷积后点数变多,为 模型,由于退化过程是卷积过程,线性卷积后点数变多,为 了方便计算,需要将各函数进行延拓,具体如下所示: 了方便计算,需要将各函数进行延拓,具体如下所示: ( , ) ; 0 1 0 1 (,) 0 ; 1 1 e f mn m A n B f mn AmM BnN ⎧ ≤ ≤− ≤≤ − = ⎨⎩ ≤ ≤ − ≤≤ − 且或 ( , ) ; 0 1 0 1 (,) 0 ; 1 1 e hmn m C n D h mn CmM DnN ⎧ ≤ ≤ − ≤≤ − = ⎨⎩ ≤ ≤ − ≤≤ − 且或 (,) ; 0 1 0 1 (,) 0 ; 1 1 e m n m A n B m n AmM BnN η η ⎧ ≤ ≤− ≤≤ − = ⎨⎩ ≤ ≤ − ≤≤ − 且或 5.1 退化模型
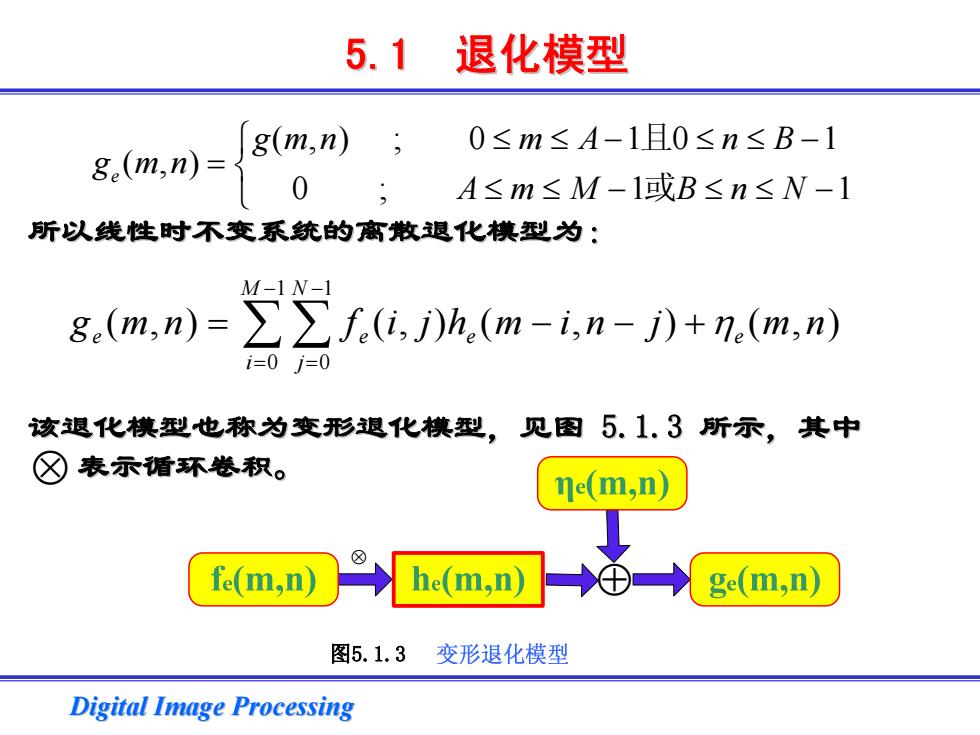
5.1 退化模型 g(m,n) 0≤m≤A-1且0≤n≤B-1 8e(m,n)= 0 A≤m≤M-1或B≤n≤N-1 所以线性时不变系统的离散退化棋型为: M-1N-1 8.(m,n)=∑∑f(i,j)h.(m-i,n-)+n.(m,n)) i=0j=0 该退化模型也称为变形退化模型,见图5.1.3所示,其中 ☒表示循环卷积。 ne(m,n) ⊕ fe(m,n he(m,n ge(m,n) 图5.1.3 变形退化模型 Digital Image Processing
Digital Image Processing Digital Image Processing 所以线性时不变系统的离散退化模型为: 所以线性时不变系统的离散退化模型为: 该退化模型也称为变形退化模型,见图 该退化模型也称为变形退化模型,见图 5.1.3 所示,其中 表示循环卷积。 表示循环卷积。 (,) ; 0 1 0 1 (,) 0 ; 1 1 e gmn m A n B g mn AmM BnN ⎧ ≤ ≤− ≤≤ − = ⎨⎩ ≤ ≤ − ≤≤ − 且或 1 1 0 0 ( , ) (, ) ( , ) ( , ) M N e e e e i j g mn f i jh m in j mn η − − = = = − ∑ ∑ − + 5.1 退化模型 ⊕ ⊗ 图5.1.3 ⊗

5.1退化模型 离牧退化模型还可以用矩阵描述 g=Hf+n 其中,f、g和门表示MN×1维的列向量,分别是由M×N维的矩 阵.(m,以g(m,)和1(m,)的各行堆积而成,如下所示: f(0,0) 8(0,0) n(0,0) fe(0,1) 8(0,1) 7e(0,1) f(0,N-1) f= 8e(0,N-1) .(0,N-1) f(1,0) 8= 8e(1,0) 7= 7e(1,0) f(1,1) 8e(1,1) 7e(1,1) f(M-1,N-1) 8e(M-1,N-1) n.(M-1,N-1) Digital Image Processing
Digital Image Processing Digital Image Processing 离散退化模型还可以用矩阵描述 离散退化模型还可以用矩阵描述 其中,f 、g和 表示MN×1维的列向量,分别是由 维的列向量,分别是由M×N维的矩 阵 、 和 的各行堆积而成,如下所示 的各行堆积而成,如下所示 : g = Hf + η (0,0) (0,1) (0, 1) (1, 0) (1,1) ( 1, 1) e e e e e e f f f N f f f fM N ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ − ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢⎣ − − ⎥⎦ # # (0,0) (0,1) (0, 1) (1, 0) (1,1) ( 1, 1) e e e e e e g g g N g g g gM N ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ − ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢⎣ − − ⎥⎦ # # (0,0) (0,1) (0, 1) (1,0) (1,1) ( 1, 1) e e e e e e N M N η η η η η η η ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ − ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢⎣ − − ⎥⎦ # # 5.1 退化模型 η e f (m,n) e g (m,n) ηe (m,n)

5.1退化模型 H为MN*N的矩阵,对于线性移不变系统具有如下特殊结构: a以2…H HHH…以 h.(i,0) h.(,N-1)… h.(6,1) H-H H H… h.(i,1) h.i,0) …h.(,2) H,= Lh.6,N-1)h6N-2) …h.i,0)N M 可以看出H是一个分块循环矩阵,而其中H:也是右移循环 阵。这是由于在卷积时利用了[h。]矩阵的周期延拓性。 Digital Image Processing
Digital Image Processing Digital Image Processing H为MN*MN的矩阵,对于线性移不变系统具有如下特殊结构: 的矩阵,对于线性移不变系统具有如下特殊结构: 可以看出H是一个分块循环矩阵,而其中 是一个分块循环矩阵,而其中Hi也是右移循环 阵。这是由于在卷积时利用了 阵。这是由于在卷积时利用了 矩阵的周期延拓性。 矩阵的周期延拓性。 0 1 -2 1 1 0 -1 2 210 3 123 0 M M M MMM M M HH H H H HH H HH H H H HHH H − −− − × ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ =⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ " " " # # # %# " ( ,0) ( , 1) ( ,1) ( ,1) ( ,0) ( ,2) ( , 1) ( , 2) ( ,0) ee e ee e i ee e N N h i h iN h i hi hi hi H hiN hiN hi × ⎡ − ⎤ ⎢ ⎥ =⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ − − ⎦ " " # # %# " e [h ] 5.1 退化模型

5.1退化模型 循环矩阵H的对角化 根据Hunt的结果,可以对H进行对角化,即H=WDW1 W是一个大小为N x MNa维的矩阵,由MXM个大小为NXN的子块 构成: Wx(O,O) wM(0,1) wM(0,M-1) wy(1,1) W Wx(1,O) Wy(I,M-1) wM(M-1,O)wM(M-1,1))· wM(M-1,M-I)) wu(i,m)=exp(j2nim/M), i,m=0,1,2,…,M-1 Wy(k,n)=exp(j2xkn/N, k,n=0,1,2,…,N-1 Digital Image Processing
Digital Image Processing Digital Image Processing 循环矩阵H的对角化 根据Hunt的结果,可以对 的结果,可以对H进行对角化,即 进行对角化,即 W是一个大小为MN×MN维的矩阵,由M×M个大小为N×N的子块 构成: -1 H = WDW (0,0) (0,1) (0, 1) (1,0) (1,1) (1, 1) ( 1,0) ( 1,1) ( 1, -1) MM M MM M MM M w w wM w w wM W wM wM wM M ⎡ ⎤ − ⎢ ⎥ − = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ −− − " " # ## # " ( , ) exp( 2 / ), w i m j im M M = π ( , ) exp( 2 / ), w kn N = j πkn N im M , 0,1, 2, , 1 = " − kn N , 0,1, 2, , 1 = " − 5.1 退化模型

5.1退化模型 从而 W=WM⑧Ww={wM(i,m)}⑧{ww(k,n)} ={exp(j2πim/M)}⑧{exp(j2πnk/N)} D是一个对角矩阵 D(.med 0 i≠k 式中[]表示对冬取燕,k0表示对N膝k取家数。 由以上各式并结合: g=W DWf+n Digital Image Processing
Digital Image Processing Digital Image Processing 从而 D是一个对角矩阵 是一个对角矩阵 由以上各式并结合: 由以上各式并结合: ⎧⎪ • ⎨⎪⎩ ≠ k M N H([ ],k mod N) ; i = k D(k,i) = N0 ;i k -1 g = WDW f + η { (, )} { (,)} {exp( 2 / )} {exp( 2 / )} W W W w im w kn MN M N j π π im M j nk N =⊗= ⊗ = ⊗ 5.1 退化模型 式中 表示对 取整,k mod N表示对N除k取余数。 kN⎡ ⎤ ⎢ ⎥ ⎣ ⎦ kN