《高等数学》课程教学资源（课件讲稿）第十二章 无穷级数 12-7 傅里叶级数

第七节 第十二章 停里叶级数 一、三角级数及三角函数系的正交性 二、函数展开成傅里叶级数 三、正弦级数和余弦级数

第七节 一、三角级数及三角函数系的正交性 二、函数展开成傅里叶级数 三、正弦级数和余弦级数 第十二章 傅里叶级数

一、三角级数及三角函数系的正交性 简单的周期运动：y=Asin(ot+p)(谐波函数) (A为振幅，o为角频率，o为初相) 00 复杂的周期运动：y=40+∑4nsin(n0t+z） n=1 (谐波迭加 An sin on cosnot+An cos on sinnot 4o=Ao.an An singn-bn=An coson=x E2 00 得函数项级数 k=1 称上述形式的级数为三角级数

一、三角级数及三角函数系的正交性 简单的周期运动 : (谐波函数) ( A为振幅, 复杂的周期运动 : A n t A n t n sinn cos   n cosn sin  令 sin , an  An n cos , bn  An n 得函数项级数 ( cos sin ) 2 1 0 a nx b nx a n n k      为角频率, φ为初相 ) (谐波迭加) 称上述形式的级数为三角级数

定理1.组成三角级数的函数系 1,cosx,sinx,cos2x,sin2x,.,cosx,sinx,. 在[-元，]上正交，即其中任意两个不同的函数之积在 [-兀，]上的积分等于0 证：∫1 cosndx=∫1 sinnxdx=0(n=l,2,） cos kx cosnx dx coskxcosnx=[cos(k+n)x+cos(k-n)x] =2[cos(k+mx+cos(k-m)x]dx=0(k≠n)） 同理可证： sin kx sin nx dx=0(k≠n） "cos kx sin nx dx =0

cos(k n)x cos(k n)x d x π 2 π 1      定理 1. 组成三角级数的函数系 证:   π π 1 cos nxd x   π π 1 sin nxd x  0 cos kx cos nxdx π π   0 sin sin 0 π π   同理可证 : kx nxdx 正交 , 上的积分等于 0 . 即其中任意两个不同的函数之积在 cos sin 0 π π   kx nxdx (k  n )

但是在三角函数系中两个相同的函数的乘积在[一兀，] 上的积分不等于0.且有 -1dr=2元 eos2nxd山=元 (n=1,2,.） 2sin2nxdk=元 cos2 nx= 1+cos 2nx 1-cos 2nx sinnx= 2 2

上的积分不等于 0 . 1 1d 2 π π π    x sin nxdx 2 π π  cos n x dx 2 π π  , 2 1 cos 2 cos2 nx nx   2 1 cos 2 sin2 nx nx   且有  π  π 但是在三角函数系中两个相同的函数的乘积在

二、函数展开成傅里叶级数 定理2，设f(x)是周期为2π的周期函数，且 00 fx)= +∑a,cosK+b,sn ① 2 n=1 右端级数可逐项积分，则有 an=∫fx)cosd (n=0,1, ② f()sinnxdx (n=1,2,. 证：由定理条件，对①在[-兀，]逐项积分，得 adz=a:-aws6nsw =a0元

二、函数展开成傅里叶级数 定理 2 . 设 f (x) 是周期为 2 的周期函数 , 且 ( cos sin ) 2 ( ) 1 0 a nx b nx a f x n n n      右端级数可逐项积分, 则有 证: 由定理条件,                 1   π π π π π π 0 π π d cos d sin d 2 ( )d n n n x a nx x b nx x a f x x ① ② 对①在 逐项积分, 得

a=f()dx ["f(x)coskxdx= coskxdx 2J-元 +2[出：4山 =axcos-kxdx=akπ (利用正交性) .a6=∫f(x)coskxdx(k=1,2,.) 类似地，用sinkx乘①式两边，再逐项积分可得 6-wsn如k=12

    kx x a f x kx x cos d 2 ( )cos d π π 0 π π        n 1   a kx nx x n cos cos d π π b kx nx x n cos sin d π π  a kx x k cos d π π 2   a f x kx x k ( )cos d π 1 π π    ( k 1, 2, ) (利用正交性)    ( )sin d ( 1, 2, ) π 1 π π      b f x kx x k k a f (x)d x 1 π π 0     类似地, 用 sin k x 乘 ① 式两边, 再逐项积分可得

00 fx)=2 an cosnx+b sin nx) ① n= a.=/)cosndx (n=0,l） ② f()sinnxdx (n=1,2,.) 不 由公式②确定的an,bn称为函数 f(x)的傅里叶系数；以f(x)的傅里 叶系数为系数的三角级数①称为 f(x)的傅里叶级数 傅里叶，J.B.J

叶系数为系数的三角级数 ① 称为 的傅里叶系数 ;        1 0 cos sin 2 ( ) n n n a nx b nx a f x    π π ( )cos d ( 0,1, ) π 1 an f x nx x n  由公式 ② 确定的 ① ② 以    π π ( )sin d ( 1, 2, ) π 1 bn f x nx x n  的傅里 的傅里叶级数 . 称为函数 简介

定理3（收敛定理，展开定理） 设f(x)是周期为2元的 周期函数，并满足狄利克雷(Dirichlet)条件 1)在一个周期内连续或只有有限个第一类间断点 2)在一个周期内只有有限个极值点 则f(x)的傅里叶级数收敛，且有 注意：函数展成 傅里叶级数的条 件比展成幂级数 的条件低得多 - f(x), x为连续点 2 其中an,bn为f(x)的傅里叶系数 ,(证明略

定理3 (收敛定理, 展开定理) 设 f (x) 是周期为2 的 周期函数, 并满足狄利克雷( Dirichlet )条件: 1) 在一个周期内连续或只有有限个第一类间断点; 2) 在一个周期内只有有限个极值点, 则 f (x) 的傅里叶级数收敛 , 且有      f (x) , , 2 ( ) ( )   f x  f x x 为间断点 其中 an bn , 为 f (x) 的傅里叶系数 . ( 证明略 ) x 为连续点 注意: 函数展成 傅里叶级数的条 件比展成幂级数 的条件低得多. 简介

例1.设f(x)是周期为2元的周期函数，它在[-π，π) 上的表达式为 = π≤x<0 0≤x<元 将f(x)展成傅里叶级数 解：先求傅里叶系数 ()cdx -（-+1 c 7 =0 (n=0,1,2

y x 例1. 设 f (x) 是周期为 2 的周期函数 , 它在 上的表达式为           1, 0 π 1, π 0 ( ) x x f x 解: 先求傅里叶系数        π 0 0 π 1 cos d π 1 ( 1)cos d π 1 nx x nx x  0 ( n  0 ,1, 2 , ) 将 f (x) 展成傅里叶级数. O 1 1  π π

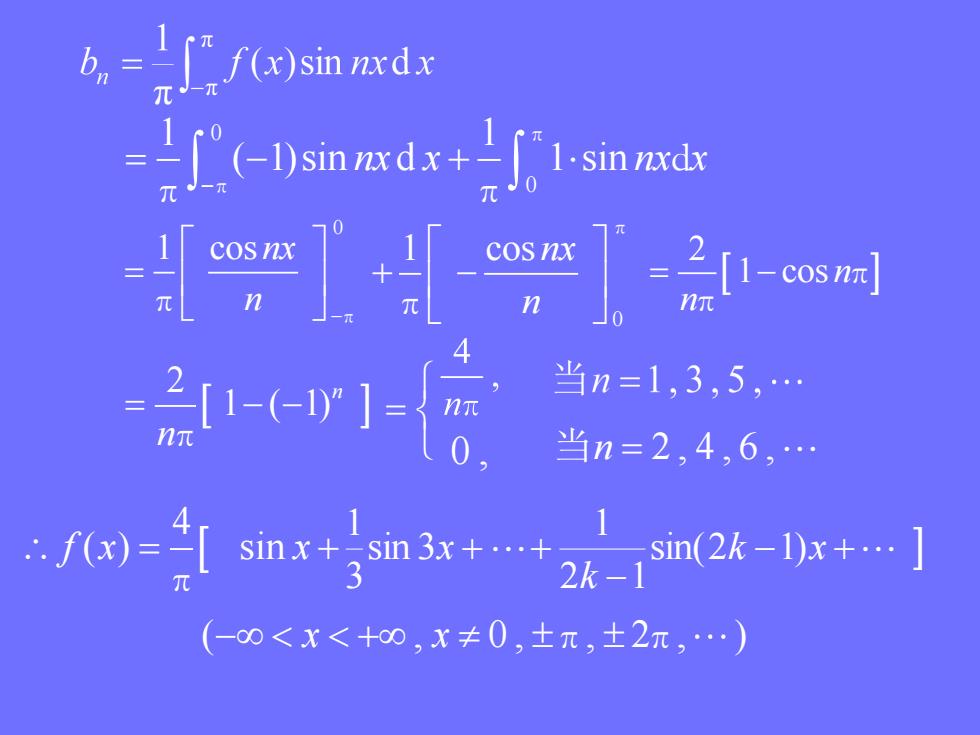
()sin dx =（-0 sn+g1 in +-时 -]-同 当n=1,3,5, 当n=2,4,6, f-snx+n3x+中 sin(2k-1)x+.] 入 (-0<x<+0,x≠0，土π，±2元，.)

0 0 1 1 ( 1)sin d 1 sin π π d π π nx x nx x        0 1 cos π π nx n         0 1 cos π π nx n           2 1 cos π π n n     2 1 ( 1) π n n        0 , 当n  2 , 4 , 6 ,   4 ( ) sin π    f x x sin 3x  3 1      k x k sin(2 1) 2 1 1  ( , 0 , , 2 , )        x x π π