《高等数学》课程教学资源（课件讲稿）第九章多元函数微分法及其应用 9-5 隐函数求导公式

第五节 第九章 隐强数的求导方法 1)方程F(xy)=O在什么条件下才能确定隐函数 例如方程x产+少+C=0{ C0时，不能确定隐函数 2)方程能确定隐函数时，研究其连续性，可微性及求导方法问题 本节讨论： 一、一个方程所确定的隐函数的条件及其导数 二、方程组所确定的隐函数组的条件及其导数

第五节 第九章 一、一个方程所确定的隐函数的条件及其导数 二、方程组所确定的隐函数组的条件及其导数 隐函数的求导方法 1) 方程F(x,y)=0在什么条件下才能确定隐函数 . 例如, 方程 C 0 时, 不能确定隐函数 2) 方程能确定隐函数时, 研究其连续性,可微性及求导方法问题. 本节讨论:

一、一个方程所确定的隐函数及其导数 定理1. 设函数F(x,y)在点P(xo,yo的某一邻域内满足 ①具有连续的偏导数： ②F(x,y0)=0 ③F,(x0,%)≠0 则方程F(x,y)=0在点x的某邻域内可唯一确定一个 单值连续函数y=f(x),满足条件yo=f(xo),并有连续 导数 dy (隐函数求导公式) dx F 就求导公式推导如下：

一、一个方程所确定的隐函数及其导数 定理1. 设函数 ( , ) 0; F x0 y0  则方程 单值连续函数 y = f (x) , 并有连续 y x F F x y   d d (隐函数求导公式) 就求导公式推导如下： ① 具有连续的偏导数; 的某邻域内可唯一确定一个 在点 的某一邻域内满足 ( , ) 0 Fy x0 y0  ② ③ 满足条件 导数

设y=f(x)为方程F(x,y)=0所确定的隐函数，则 F(x,f(x)≡0 两边对x求导 OF,oFdy =0 Ox Oy dx 在(x0,)的某邻域内F,≠0 dy F dx F

两边对 x 求导 y x F F x y   d d 在 的某邻域内 Fy  0 则 F x yx

若F(x,y)的二阶偏导数也都连续， dy 则还可求隐函数的二阶导数： dx F X dy-2(- 、dy d FxxFy-FxxFx FxyFy-Fy F F FxEy2-2ExExFy+EyyFx F

若F( x , y ) 的二阶偏导数也都连续,  2 2 d d x y 2 y xx y yx x F F F  F F   3 2 2 2 y xx y xy x y y y x F F F  F F F  F F   y x F F x y   d d ( ) y x F F y     ( ) 2 y x y xy y y y x F F F F F F F    二阶导数 : ( ) y x F F x    x y x x y d d  则还可求隐函数的

例1.验证方程siny+ex-xy-1=0在点(0,0)某邻域 可确定一个单值可导隐函数y=f(x),并求 到。dy =0 deir=o 解：令F(x,y)=siny+e-xy-1,则 ①F=ex-y,F,=cosy-x连续， ②F(0,0)=0; ③F,(0,0)=1≠0， 由定理1可知，在x=0的某邻域内方程存在单值可 导的隐函数y=f(x),且

例1. 验证方程 在点(0,0)某邻域 可确定一个单值可导隐函数 d 0 d , d 0 d 2 2  x x  y x x y 解: 令 F(x, y)  sin y  e  xy 1, x F(0,0)  0; F e y, x x   连续 ; 由 定理1 可知, Fy (0,0) 1  0, ① 导的隐函数 则 F y x y  cos  ② ③ 在 x = 0 的某邻域内方程存在单值可 且 并求

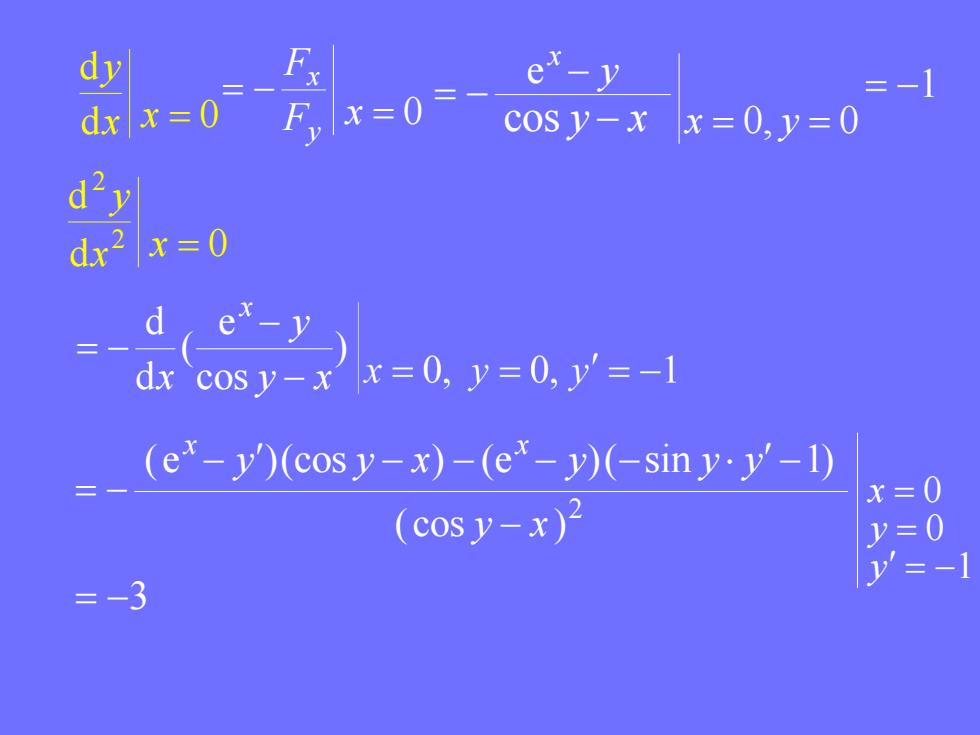
y e"-y x=0 x=0 cos y-x x=0,y=0 d-y dr2 x=0 d e-y） dx cosy-xx=0,y=0,y'=-1 (ex-y)(cosy-x)-(ex-y)(-siny.y'-1) x=0 (cosy-x)月 V =0 =-3

F e y, x x   F y x y  cos  d 0 d x x  y  0   F x F y x   cos y  x y x e  x  0, y  0 d 0 d 2 2 x x  y ) cos e ( d d y x y x x      3 1 0 0      y y x (e y ) x   (cos y  x) (e y) x   (sin y  y  1) F(x, y)  sin y  e  xy 1  0 x 2 (cos ) y  x  

导数的另一求法一利用隐函数求导 siny+e*-xy-1=0,y=y(x) 两边对x求导 x=0 ex-y cosy.y'+e*-y-xy'=O cosy-x(0,0) 两边再对x求导 =-1 -siny.(y)2+cosy.y"+ex-y'-y'-xy"=0 令x=0,注意此时y=0,y'=-1 d2y dx2 =0-3

 0  x y 3 d 0 d 2 2   x x  y sin y e xy 1 0, y y(x) x      两边对 x 求导 两边再对 x 求导 sin y (y )  cos y  y  2 令 x = 0 , 注意此时 y  0 , y   1 cos (0,0) e y x y x     导数的另一求法 — 利用隐函数求导

定理2，若函数F(x,y,z)满足： ①在点P(xo,y0,20)的某邻域内具有连续偏导数； ②F(0,0,20)=0; ③F(0,0,0)≠0， 则方程F(x,y,2)=0在点(xo,0)某一邻域内可唯一确 定一个单值连续函数：=f(x,),满足20=∫(x0,V0), 并有连续偏导数 x F’ dy F 就求导公式推导如下

定理2 . 若函数 F(x, y,z) z y z x F F y z F F x z         , 的某邻域内具有连续偏导数 ; 则方程 在点 并有连续偏导数 定一个单值连续函数 z = f (x , y) , 就求导公式推导如下: 满足 ( , , ) 0 ; F x0 y0 z0  ( , , ) 0 , Fz x0 y0 z0  ① 在点 满足: ② ③ 某一邻域内可唯一确

设z=∫(x,y)是方程F(x,y)=0所确定的隐函数，则 F(x,y,f(x,y)≡0 两边对x求偏导 Fx+F: 0z =0 8x 在(xo,y0,20)的某邻域内F≠0 a F Fy 同样可得 F

F(x, y , f (x, y ) )  0 两边对 x 求偏导 Fx z x F F x z     z y F F y z     同样可得 则  Fz x z    0 F x y x y z

例2.设x2+y2+z2-4z=0,求 解法1利用隐函数求导 。z 2x+2z -4 0z - =0 8x 8x 2-2 再对x求导 2+2 022 ∂2 2+2 -4 x 82z 1+ &r2 2-2 (2-z)3

例2. 设 4 0, 2 2 2 x  y  z  z  解法1 利用隐函数求导 2 2 4  0       x z x z x z z x x z     2 2 4 0 2 2     x z 2 1 ( ) x z    . 2 2 x z   求 再对 x 求导