
第四节 第八章 空间直孩及其方程 一、空间直线方程 二、线面间的位置关系 三、杂例
第四节 一、空间直线方程 二、线面间的位置关系 空间直线及其方程 第八章 三、杂例

一、空间直线方程 1.一般式方程 直线可视为两平面交线,因此其一般式方程 Ax+By+C+D=0 42x+B2y+C22+D2=0 (不唯一)
一、空间直线方程 x y z O 0 A1x B1 y C1 z D1 1 2 L 因此其一般式方程 1. 一般式方程 直线可视为两平面交线, (不唯一)

2.对称式方程 己知直线上一点M0(xo,0,20)和它的方向向量 s=(m,n,p),设直线上的动点为M(x,y,z) 则 MoM//S M(x,y,2) 故有 x-0=y-y0= 2-20 m n p M(x0,y0,20 此式称为直线的对称式方程(也称为点向式方程 说明:某些分母为零时,其分子也理解为零.↑2 例如,当m=n=0,p≠0时,直线方程为 x=X0 y=yo
z y x 0 x 0 y O ( , , ) 0 0 0 0 M x y z 2. 对称式方程 故有 说明: 某些分母为零时, 其分子也理解为零. m x x 0 0 0 y y x x 设直线上的动点为 则 M ( x, y, z) n y y 0 p z z 0 此式称为直线的对称式方程(也称为点向式方程) 直线方程为 已知直线上一点 ( , , ) 0 0 0 0 M x y z M (x, y,z) 例如, 当 m n 0, p 0 时, 和它的方向向量 s

3.参数式方程 设 x-X0_y-Y 2- 2-20 m n p 得参数式方程: x=xo+mt y=y0+nt 2=20+p1
3. 参数式方程 设 得参数式方程 : t p z z n y y m x x 0 0 0 x x mt 0 y y n t 0 z z p t 0

设直线=y、 则该直线为( ) 0 2-1 (A)过原点且垂直于x轴 (B)过原点且平行于x轴 (C)不过原点但垂直于x轴 (D)不过原点但平行于x轴 过点M(11,-5)且与平面3x-y+z+1=0垂直的直线方程是() A. x+3_y-1_z+1 B x-3_y+1z-1 11-5 11-5 x+1y+1z-5 D.-1=y-1+5 3-11 3=-11

例1.用对称式及参数式表示直线 x+y+z+1=0 2x-y+3z+4=0 解:先在直线上找一点, 令x=1,解方程组 -3=6,得y=0,:=-2 y+2=-2 故(1,0,-2)是直线上一点 再求直线的方向向量s 交已知直线的两平面的法向量为 n1=(1,1,1),n2=(2,-1,3) s1n1,31n2.s=m×n购
例1.用对称式及参数式表示直线 解:先在直线上找一点. 3 6 2 y z y z 再求直线的方向向量 令 x = 1, 解方程组 ,得 y 0 , z 2 交已知直线的两平面的法向量为 是直线上一点 . s . 1 2 s n ,s n 1 2 s n n

方 s=nxn2 三 111 =(4,-1,-3) 2-13 故所给直线的对称式方程为 x-l y z+2 二 4-1 -3 x=1+41 参数式方程为 = z=-2-31 解题思路:先找直线上一点: (1,0,-2) 再找直线的方向向量 是直线上一点
故所给直线的对称式方程为 参数式方程为 t 4 x 1 1 y 解题思路: 先找直线上一点; 再找直线的方向向量. (4, 1, 3) 1 2 s n n 2 1 3 1 1 1 i j k 是直线上一点

x-y+z=1, 设直线L的方程为 则的参数方程为(): 2x+y+z=4, x=1-2t, x=1-2t x=1-2t, x=1-2t, A. y=1+t, B.y=-1+t, C. y=1-t, D y=-1-t) z=1+3t z=1+3t z=1+3t z=1+3t
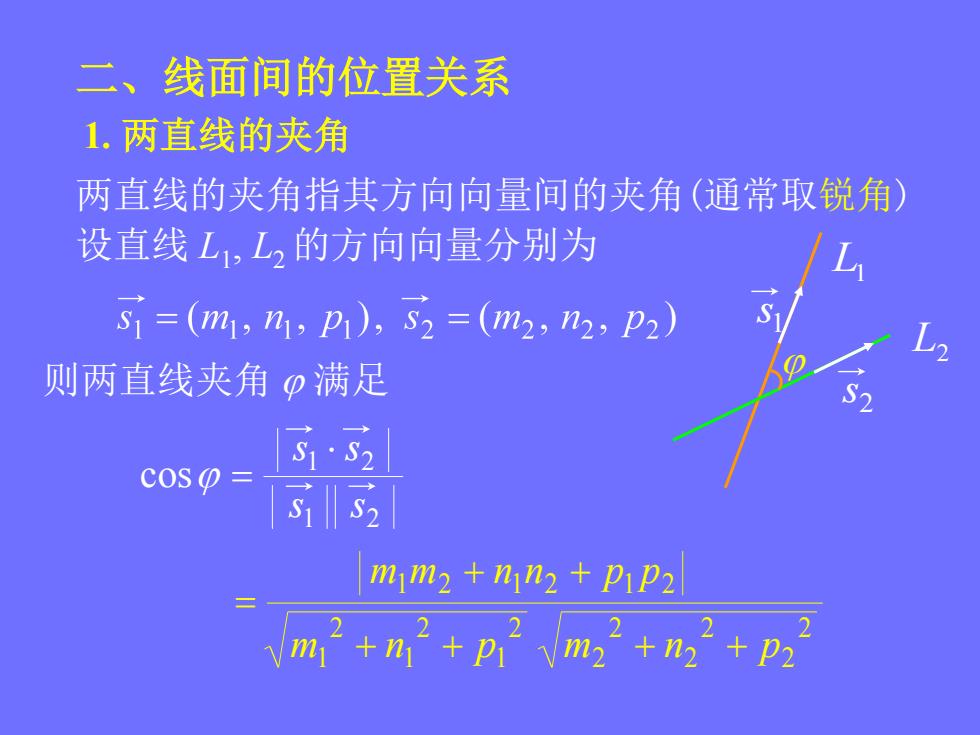
二、线面间的位置关系 1.两直线的夹角 两直线的夹角指其方向向量间的夹角(通常取锐角) 设直线L,L,的方向向量分别为 S1=(m1,h1,p1),S2=(m2,n2,P2) 则两直线夹角φ满足 cos 2 mim2+nn2+pip2 2 2 2 m1+n+p1vm2+n2+p2
L2 L1 二、线面间的位置关系 1. 两直线的夹角 则两直线夹角 满足 设直线 L1 , L2 的方向向量分别为 两直线的夹角指其方向向量间的夹角(通常取锐角) 1 2 1 2 1 2 m m n n p p 2 1 2 1 2 1 m n p 2 2 2 2 2 2 m n p 1 2 1 2 cos s s s s 1 s 2 s

特别有: (1)L⊥L2= 5112 =m1m2+n1n2+p1p2=0 (2)L111L2 5ll52 S 1=h1=P1 m2 n2 P2 s=(m1,n1,p) 32=(m2,n2,P2)
特别有: 1 2 (1) L L 1 2 (2) L // L 0 m1m2 n1n2 p1 p2 2 1 2 1 2 1 p p n n m m 1 2 s s 1 2 s //s L2 L1 1s 2s L2 L1 1s 2s