第13章 非正弦周期电流电路 和信号的频谱 本章重点 13.1 非正弦周期信号 13.2 周期函数分解为傅里叶级数 13.3 有效值、平均值和平均功率 13.4 非正弦周期电流电路的计算 13.5 对称三相电路中的高次谐波 首页
第13章 非正弦周期电流电路 13.1 非正弦周期信号 13.2 周期函数分解为傅里叶级数 13.3 有效值、平均值和平均功率 13.4 非正弦周期电流电路的计算 13.5 对称三相电路中的高次谐波 首 页 本章重点 和信号的频谱

·重点 1.周期函数分解为傅里叶级数 2.非正弦周期函数的有效值和平均功率 3.非正弦周期电流电路的计算 返回
2. 非正弦周期函数的有效值和平均功率 重点 3. 非正弦周期电流电路的计算 1. 周期函数分解为傅里叶级数 返 回

13.1 非正弦周期信号 生产实际中,经常会遇到非正弦周期电流电 路。在电子技术、自动控制、计算机和无线电技 术等方面,电压和电流往往都是周期性的非正弦 波形。 非正弦周期交流信号的特点 (1) 不是正弦波 (2)按周期规律变化 ◆f(t)=f(t+nT) 返回 上页 下页
13.1 非正弦周期信号 生产实际中,经常会遇到非正弦周期电流电 路。在电子技术、自动控制、计算机和无线电技 术等方面,电压和电流往往都是周期性的非正弦 波形。 非正弦周期交流信号的特点 (1) 不是正弦波 (2) 按周期规律变化 f (t) f (t nT) 返 回 上 页 下 页
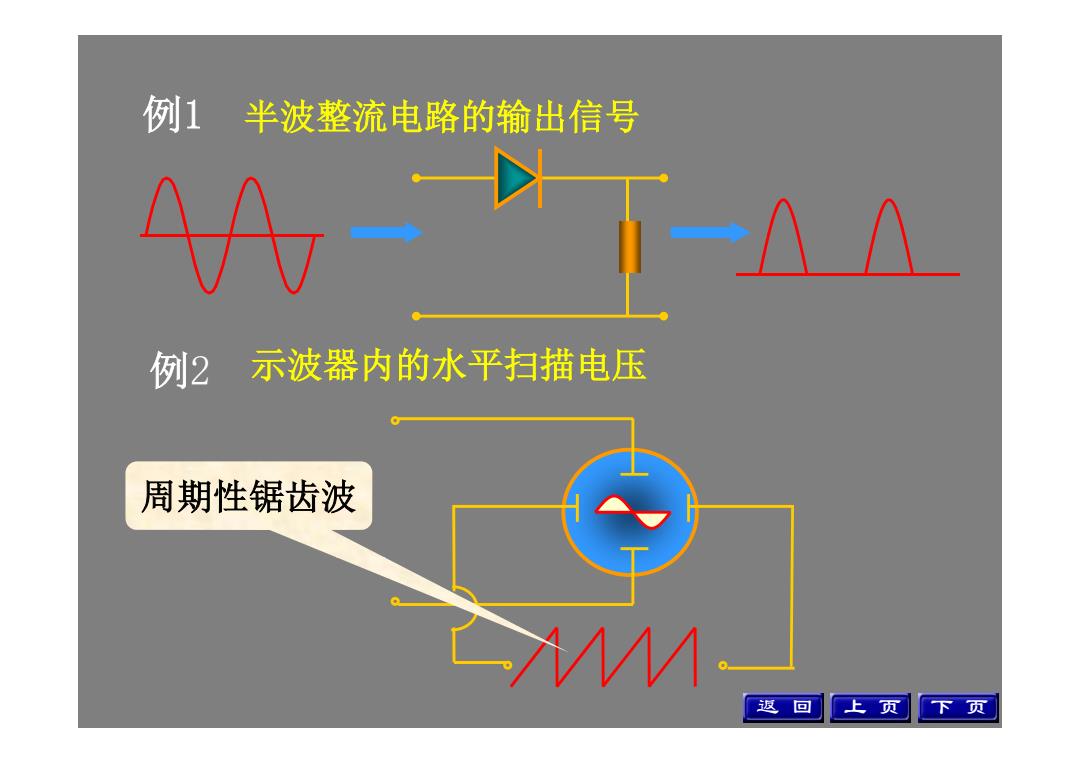
例1 半波整流电路的输出信号 4-1-4 例2: 示波器内的水平扫描电压 周期性锯齿波 Λ 返回 上页 下页
例2 示波器内的水平扫描电压 周期性锯齿波 上 页 下 页 例1 半波整流电路的输出信号 返 回
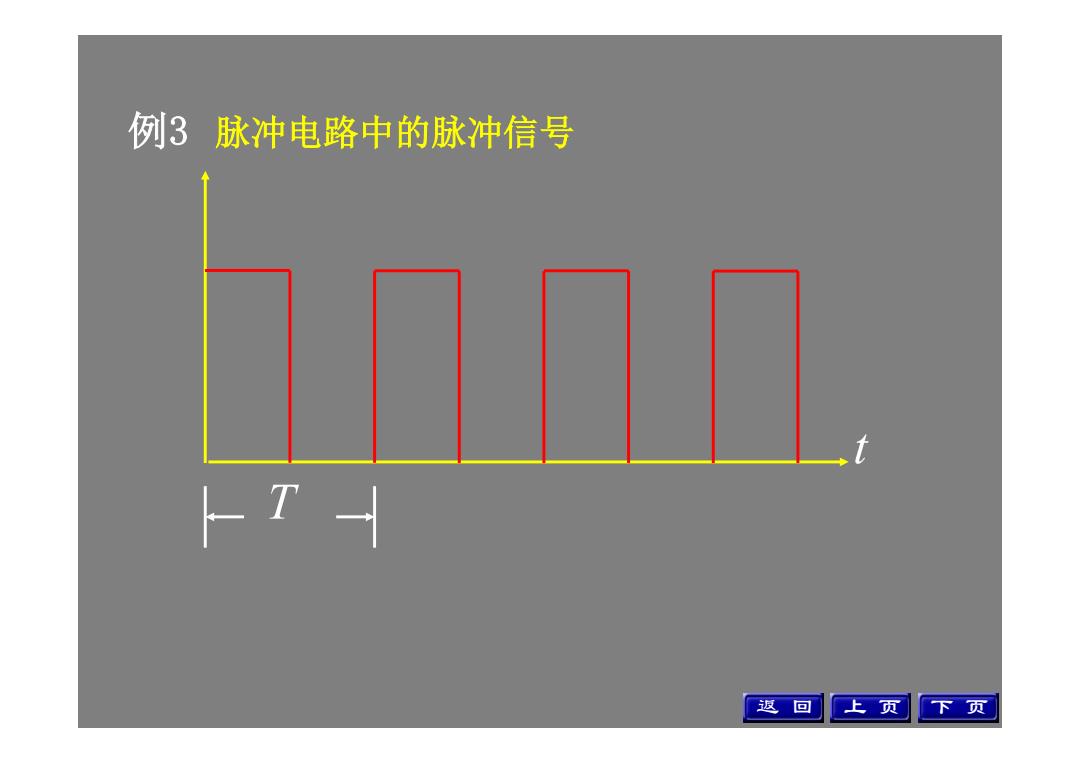
例3脉冲电路中的脉冲信号 T 返回 上页 下页
脉冲电路中的脉冲信号 T t 例3 返 回 上 页 下 页
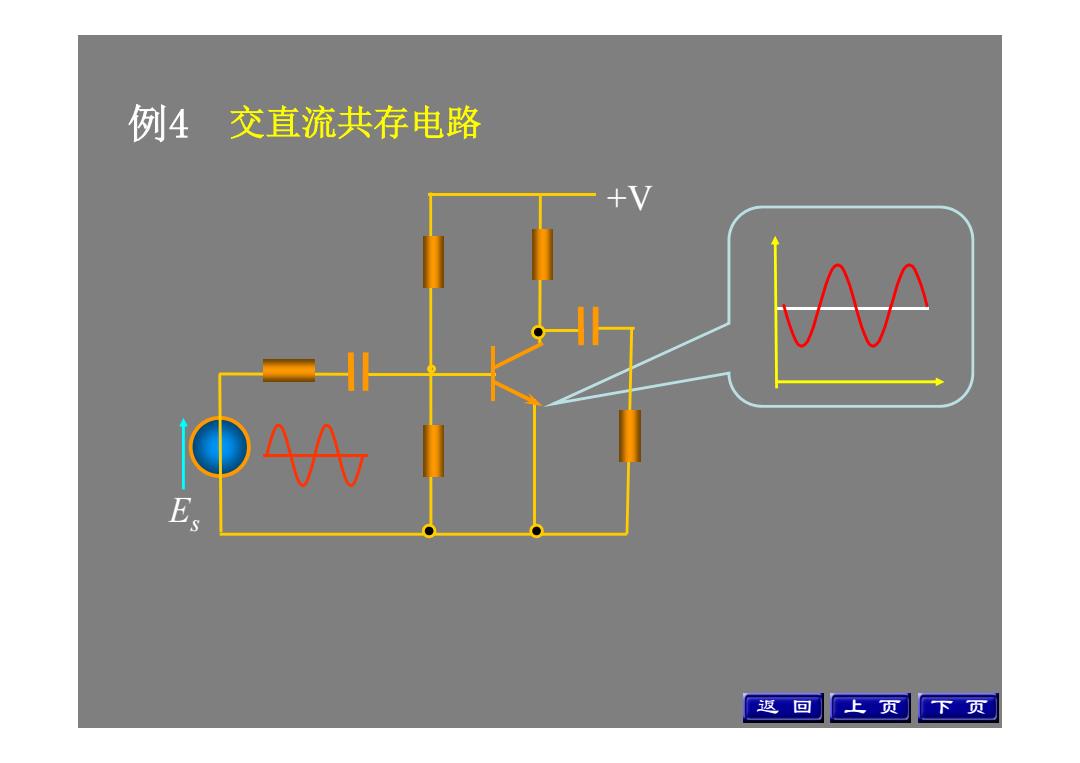
例4交直流共存电路 A ①AA 返回 上页 下页
例4 交直流共存电路 +V Es 返 回 上 页 下 页

13.2周期函数分解为傅里叶级数 若周期函数满足狄利赫利条件: ①周期函数极值点的数目为有限个: ②间断点的数目为有限个; ③在一个周期内绝对可积,即: [f(t)dt 0 可展开成收敛的傅里叶级数 般电工里遇到的周期函数都能满足 狄利赫利条件。 返回 上页 下页
13.2 周期函数分解为傅里叶级数 f t t T ( ) d 0 若周期函数满足狄利赫利条件: ①周期函数极值点的数目为有限个; ②间断点的数目为有限个; ③在一个周期内绝对可积,即: 可展开成收敛的傅里叶级数 注意 一般电工里遇到的周期函数都能满足 狄利赫利条件。 返 回 上 页 下 页

周期函数展开成傅里叶级数: 直流分量 基波(和原 f(t)=A+A cos(@t+) 函数同频) +4mc0s(20,t+4,)+ 二次谐波 (2倍频) +A cos(not+)+ 高次谐波 f(t)=A,+∑Acos(kt+) 返回 上页 下页
直流分量 基波(和原 函数同频) 二次谐波 (2倍频) 高次谐波 ( ) cos( ) 1 0 1 k km k f t A A kt f (t) A0 A1m cos(1 t 1 ) A2m cos(21 t 2 ) A nm cos(n1 t n ) 周期函数展开成傅里叶级数: 返 回 上 页 下 页

也可表示成: A cos(ko,t+)=a cos ko,t+b sin ko,t 00 f(t)=a+>[a,cosko,t+bsin kot] k=1 系数之间的关系为: =a A 二个 aj+b a, FAmC0S b=-Am sin o =arctan -b 返回 上页 下页
( ) [ cos sin ] 1 1 0 1 f t a a k t b k t k k k A k t a k t b k t km 1 k k 1 k 1 cos( ) cos sin 也可表示成: k k k k km k k km k km k k a b a A b A A a b A a arctan cos sin 2 2 0 0 系数之间的关系为: 返 回 上 页 下 页

系数的计算: A=a=TSf(Odt a, f()cs(kd() 入 bk=· f(t)sin(kot)d(@,t) 求出4o、4、b便可得到原函数)的展开式。 返回 上页 下页
2π 0 1 1 2π 0 1 1 0 0 0 ( )sin( )d( ) π 1 ( )cos( )d( ) π 1 ( )d 1 b f t k t t a f t k t t f t t T A a k k T 求出A0 、ak 、bk 便可得到原函数 f(t) 的展开式。 系数的计算: 返 回 上 页 下 页