
信号与图像处理基础 Wavelet Analysis 中国科学技术大学自动化系 曹洋
University of Science and Technology of China 信号与图像处理基础 中国科学技术大学 自动化系 曹 洋 Wavelet Analysis

主要内容 1.小波介绍 3.哈尔小波变换 1.1小波简史 4.二维哈尔小波变换 1.2小波概念 4.1二维小波变换举例 1.3小波分析 4.2二维小波变换方法 1.4小波定义 5.图像多分辨率表示 2.哈尔函数 6.小波变换的多分辨率分 2.1哈尔基函数 析特性 2.2哈尔小波函数 7.小波变换在图像边缘检 测中的应用 2.3函数的规范化 2.4哈尔基的结构 8.小波变换在图像去噪中 的应用
主要内容 1. 小波介绍 1.1 小波简史 1.2 小波概念 1.3 小波分析 1.4 小波定义 2. 哈尔函数 2.1 哈尔基函数 2.2 哈尔小波函数 2.3 函数的规范化 2.4 哈尔基的结构 3. 哈尔小波变换 4. 二维哈尔小波变换 4.1 二维小波变换举例 4.2 二维小波变换方法 5. 图像多分辨率表示 6. 小波变换的多分辨率分 析特性 7.小波变换在图像边缘检 测中的应用 8.小波变换在图像去噪中 的应用
1.小波介绍 小波(wavelet)是什么 ·在有限时间范围内变化且其平均值为零的数学函数 ·具有有限的持续时间和突变的频率和振幅 ·在有限的时间范围内,它的平均值等于零 0.5 05 AAAAN Sine wave Haar Wavelet Mexican Hat Wavelet Morlet Wavelet (sum of two Gaussians) (Gaussian-gated sine wave)
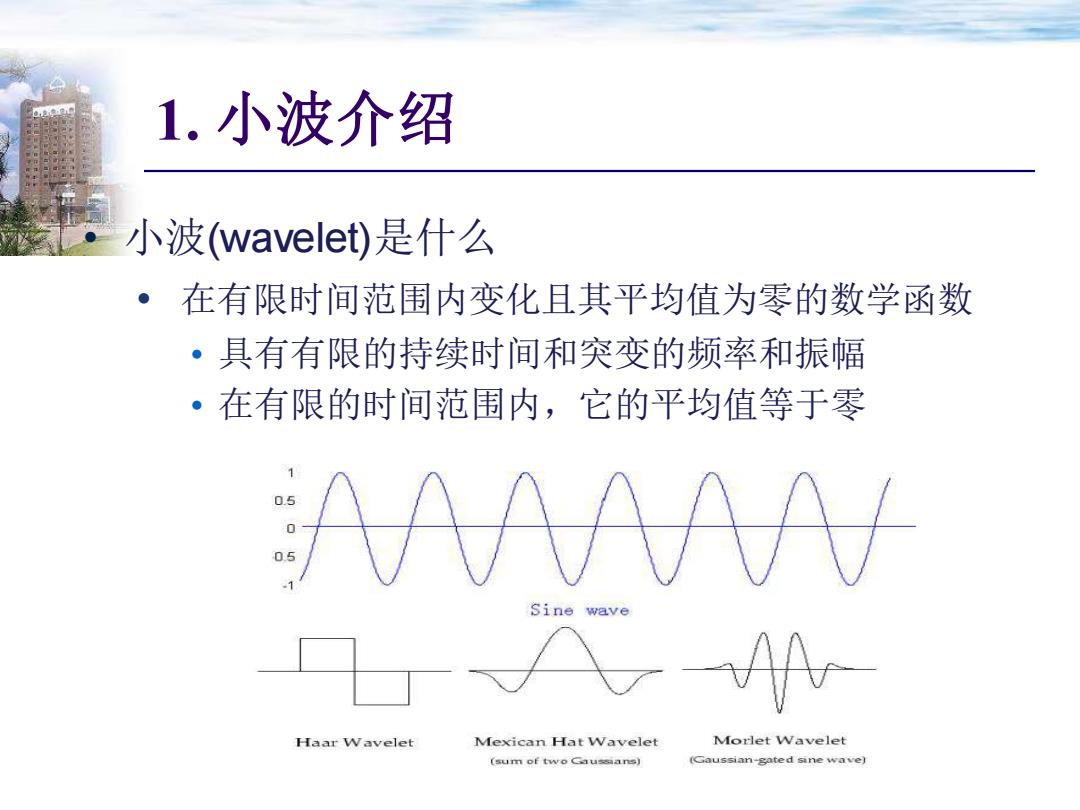
1. 小波介绍 • 小波(wavelet)是什么 • 在有限时间范围内变化且其平均值为零的数学函数 • 具有有限的持续时间和突变的频率和振幅 • 在有限的时间范围内,它的平均值等于零
1.小波介绍(续1) 部分小波 ·许多数缩放函数和小波函数以开发者的名字命名,例如, ·Moret小波函数是Grossmann和Morlet在1984年开发的 ·db6缩放函数和db6小波函数是Daubechies?开发的 Moret小波函数 Mexican Hat小波函数 Meyer缩放函数 Meyer.小波函数 Haar缩放函数 Haar小波函数 08 1 642 0.5 0.5 0.5 0.5 0 0 0 02 0.5 0.5 -0.5 -0.5 5 05 0.5 db6缩放函数 b6小波函数 sm6缩放函数 sm6小波涵数 co1f2缩放函数 coif2小波函数 1 15 1.5 15 1.5 1 0.5 0.5 1 0.5 0.5 0.5 0 0 0 0 0 -0.5 -0.5 0.5 -0.5 0.5 1 -1 -1 10 5 10 0 10 0 5 10 5 0 图7-1正弦波与小波 —部分小波
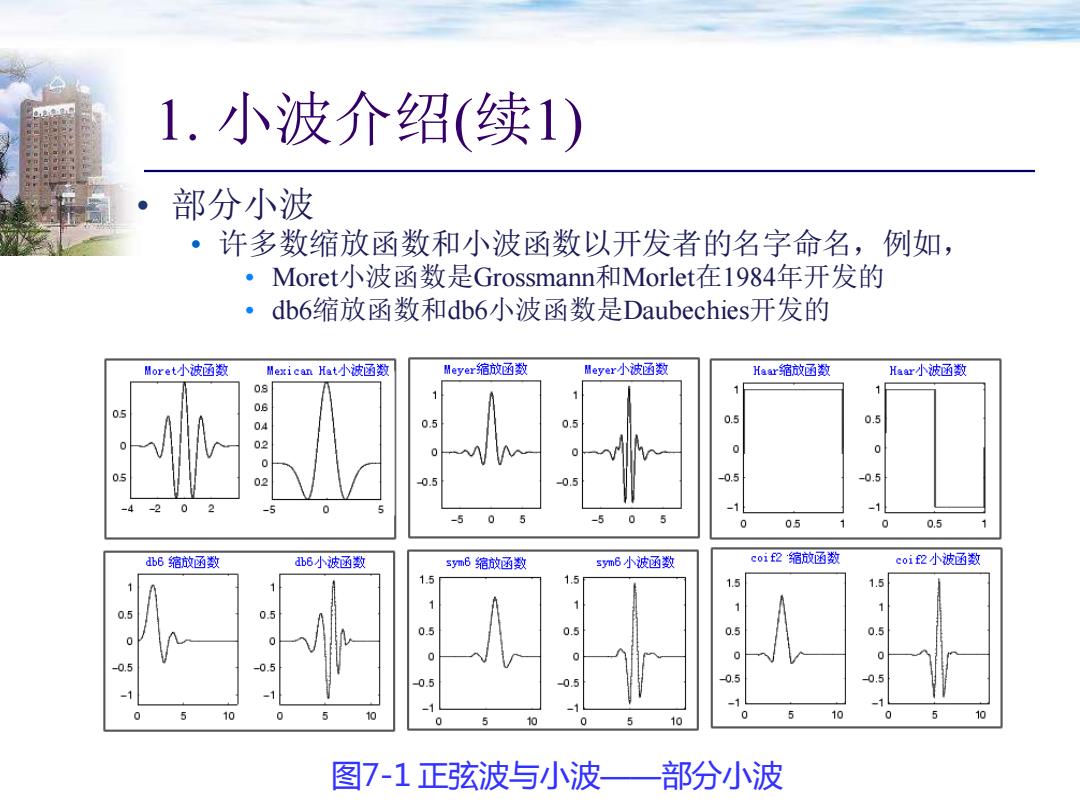
1. 小波介绍(续1) • 部分小波 • 许多数缩放函数和小波函数以开发者的名字命名,例如, • Moret小波函数是Grossmann和Morlet在1984年开发的 • db6缩放函数和db6小波函数是Daubechies开发的 图7-1 正弦波与小波——部分小波

1.小波介绍(续2) 小波简史 >小波变换(wavelet transform)是什么 老课题:函数的表示方法 .新方法:Fourier-Haar-wavelet transform 1807:Joseph Fourier 傅立叶理论指出,一个信号可表示成一系列正弦 和余弦函数之和,叫做傅立叶展开式
1. 小波介绍(续2) ➢ 1807: Joseph Fourier ◼ 傅立叶理论指出,一个信号可表示成一系列正弦 和余弦函数之和,叫做傅立叶展开式 ◼ 小波简史 ➢ 小波变换 (wavelet transform)是什么 ◼ 老课题:函数的表示方法 ◼ 新方法:Fourier-Haar-wavelet transform

1.小波介绍(续3) F(o)=∫ft)edt 0」roje where ei=cosot-jsin ot ■只有频率分辨率而没有时间分辨率 可确定信号中包含哪些频率的信号,但不能 确定具有这些频率的信号出现在什么时候 丢失了信号的时频域的局部特性,而这正是 非平稳信号最重要的性质
1. 小波介绍(续3) where cos sin j t e t j t − = − ( ) ( ) ( ) ( )e j t j t F f t e dt f t F + − − + − = = 1 2 ◼ 只有频率分辨率而没有时间分辨率 ◼ 可确定信号中包含哪些频率的信号,但不能 确定具有这些频率的信号出现在什么时候 ◼ 丢失了信号的时频域的局部特性,而这正是 非平稳信号最重要的性质
1.小波介绍(续3) 600 0 FFT 400 面布演角编面布前00 150 200 280 Titue,ms x(=cos(2π*10t+c0s(2m*25t) +c0s(2*500+c0s(2π*100t) 10,25,5Q.99辑
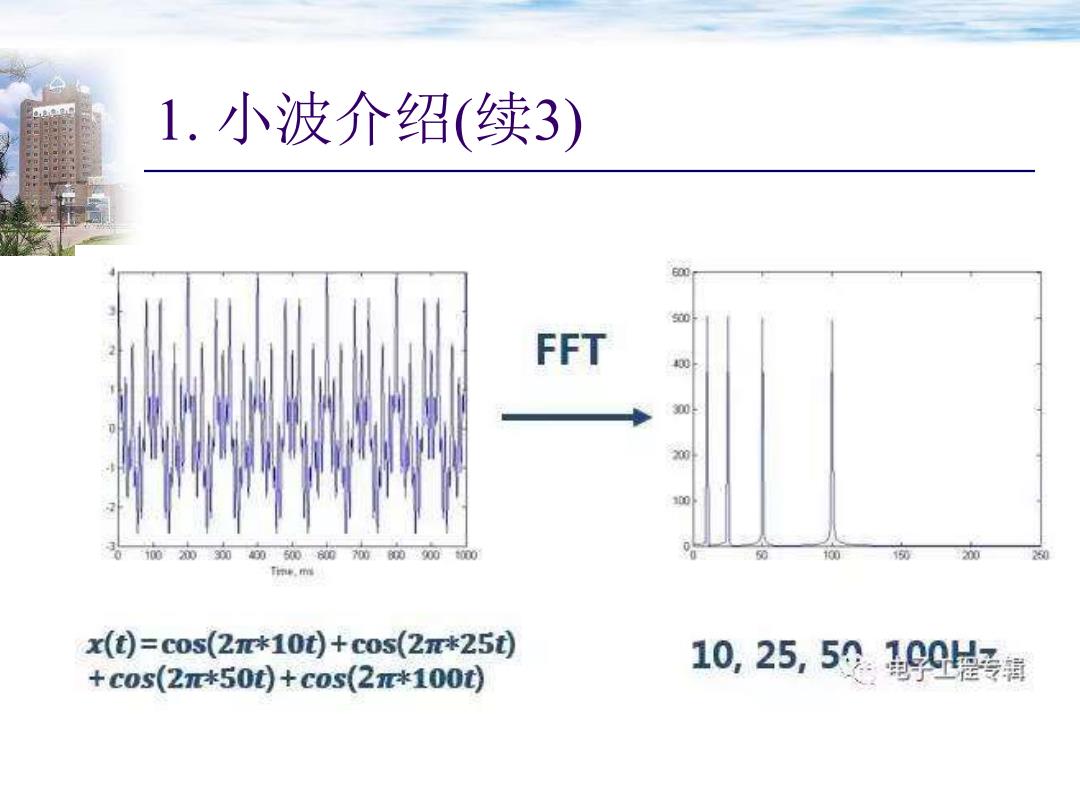
1. 小波介绍(续3)
1.小波介绍(续3) FFT FFT FFT 电子工程专
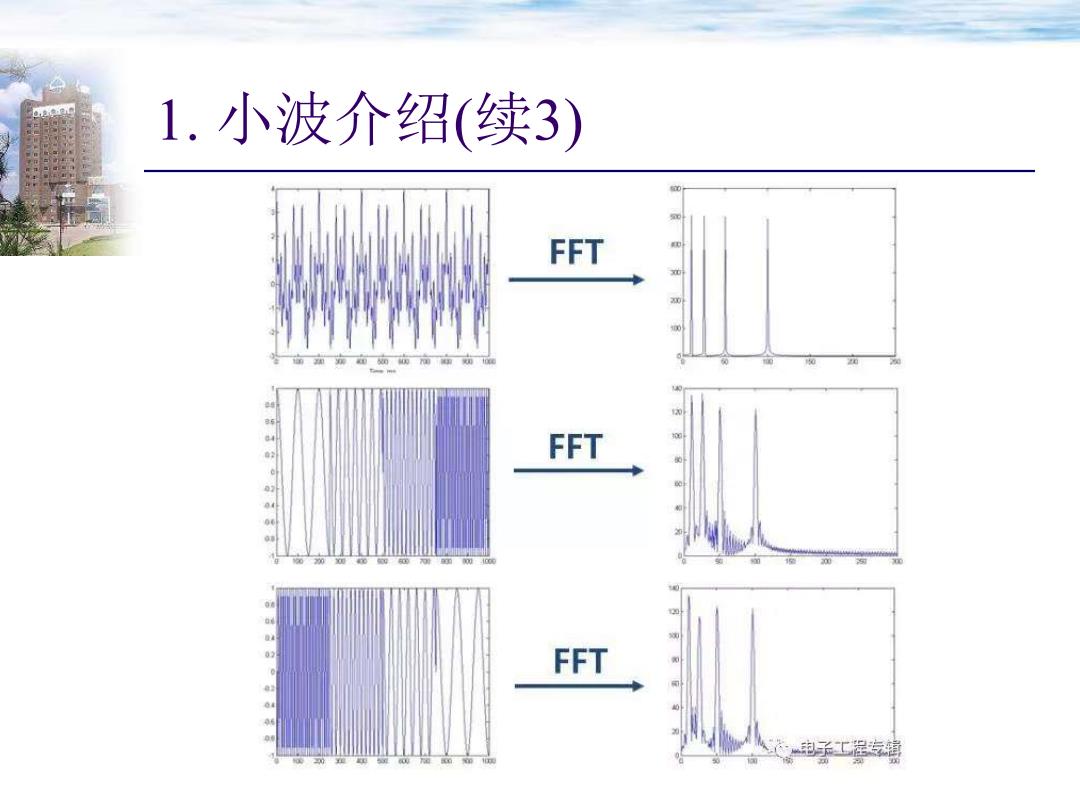
1. 小波介绍(续3)

1.小波介绍(续4) 。1945:Gabor ·开发了STFT(short time Fourier transform) STFT(r,0)=s(t)g(t-t)edt where:s(t)=signal g(t)=windowing function ws f 装 五 时间 STFT的时间-频率关系图
1. 小波介绍(续4) • 1945: Gabor • 开发了STFT (short time Fourier transform) ( , ) ( ) where: ( ) signal ( )= windo ( wing ) function j t STFT s t e dt g s t g t t − = = − STFT的时间-频率关系图
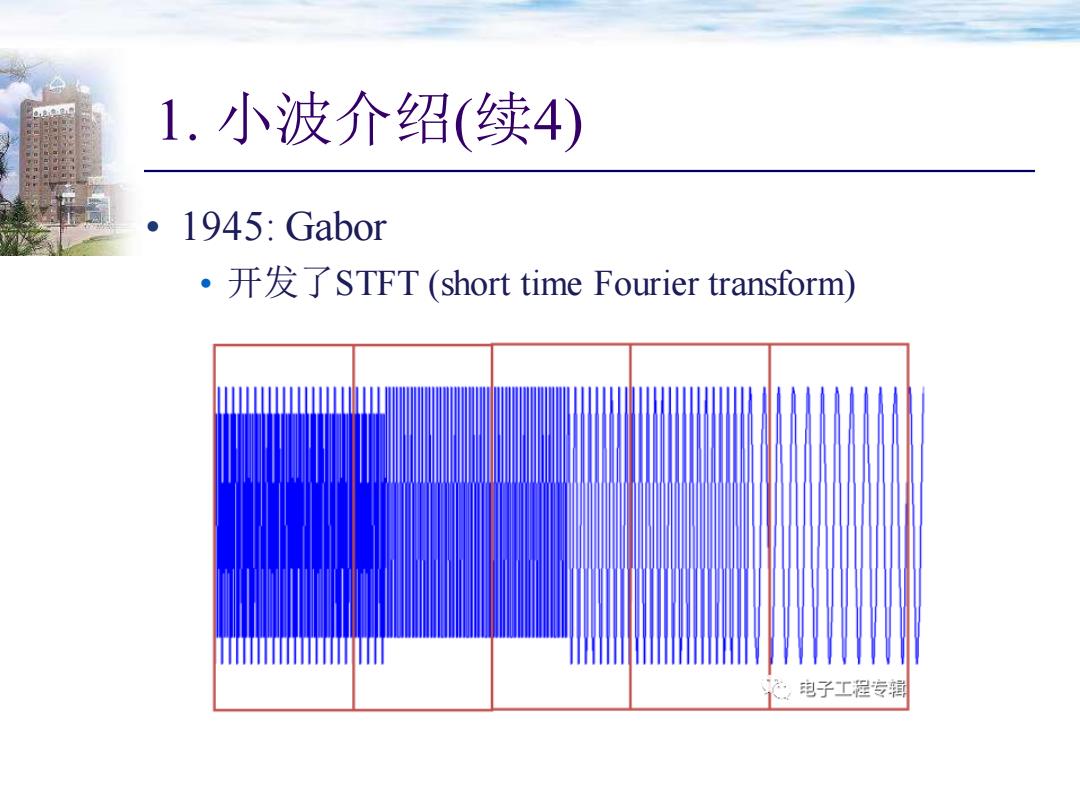
1.小波介绍(续4) .1945:Gabor ·开发了STFT(short time Fourier transform) :电子工程专辑
1. 小波介绍(续4) • 1945: Gabor • 开发了STFT (short time Fourier transform)