
第六章基于特征的图像对准
第六章 基于特征的图像对准

图像对准-Image alignment
图像对准-Image alignment

图像对准的应用 全景拼接Panorama stitching 目标识别
图像对准的应用 全景拼接 Panorama stitching 目标识别

图像拼接的困难 小区域重叠 亮度变化 遮挡, 混乱
图像拼接的困难 小区域重叠 遮挡, 混乱 亮度变化
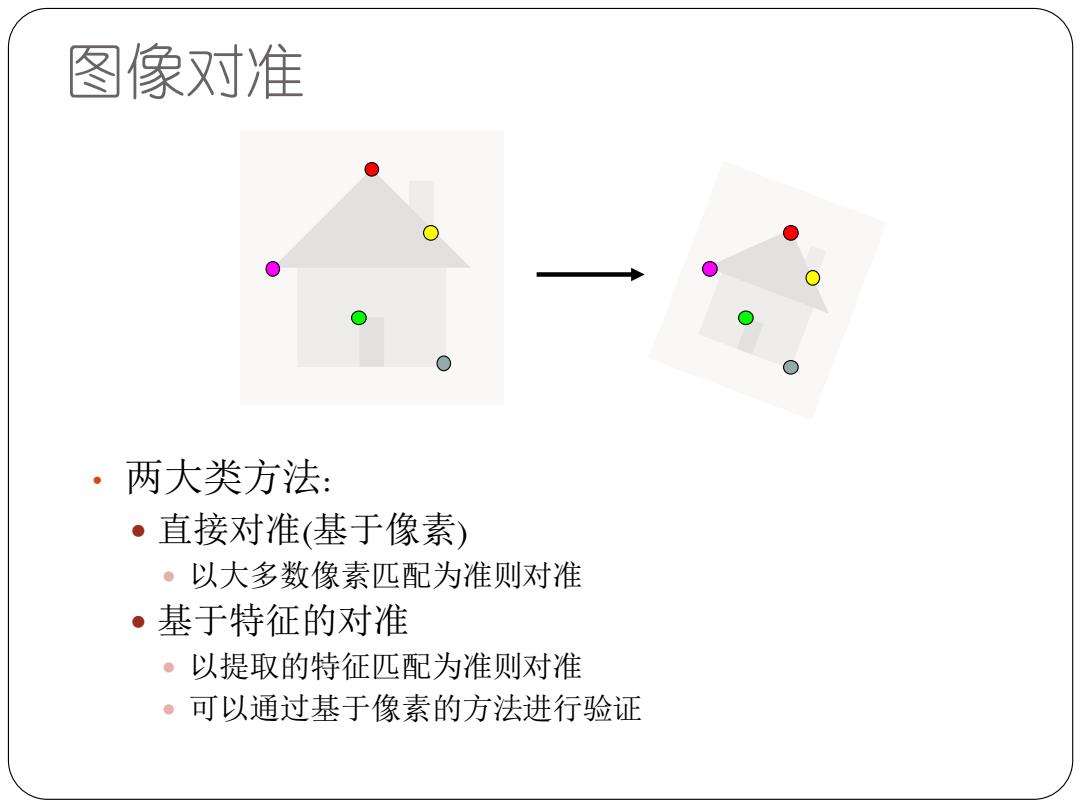
图像对准 ·两大类方法: ·直接对准(基于像素) 。以大多数像素匹配为准则对准 ·基于特征的对准 ·以提取的特征匹配为准则对准 。可以通过基于像素的方法进行验证
图像对准 • 两大类方法: 直接对准(基于像素) 以大多数像素匹配为准则对准 基于特征的对准 以提取的特征匹配为准则对准 可以通过基于像素的方法进行验证
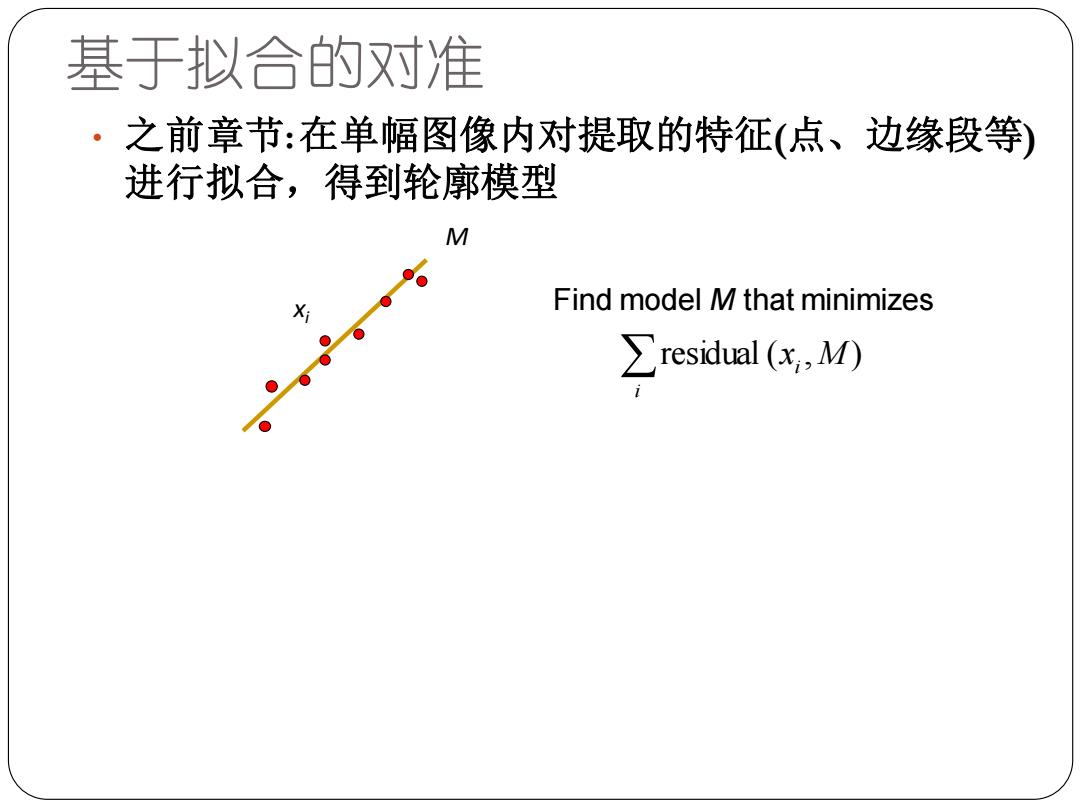
基于拟合的对准 。 之前章节:在单幅图像内对提取的特征(点、边缘段等) 进行拟合,得到轮廓模型 M Find model M that minimizes ∑residual(c,M)
基于拟合的对准 i residual (xi ,M ) • 之前章节: 在单幅图像内对提取的特征(点、边缘段等) 进行拟合,得到轮廓模型 Find model M that minimizes M xi
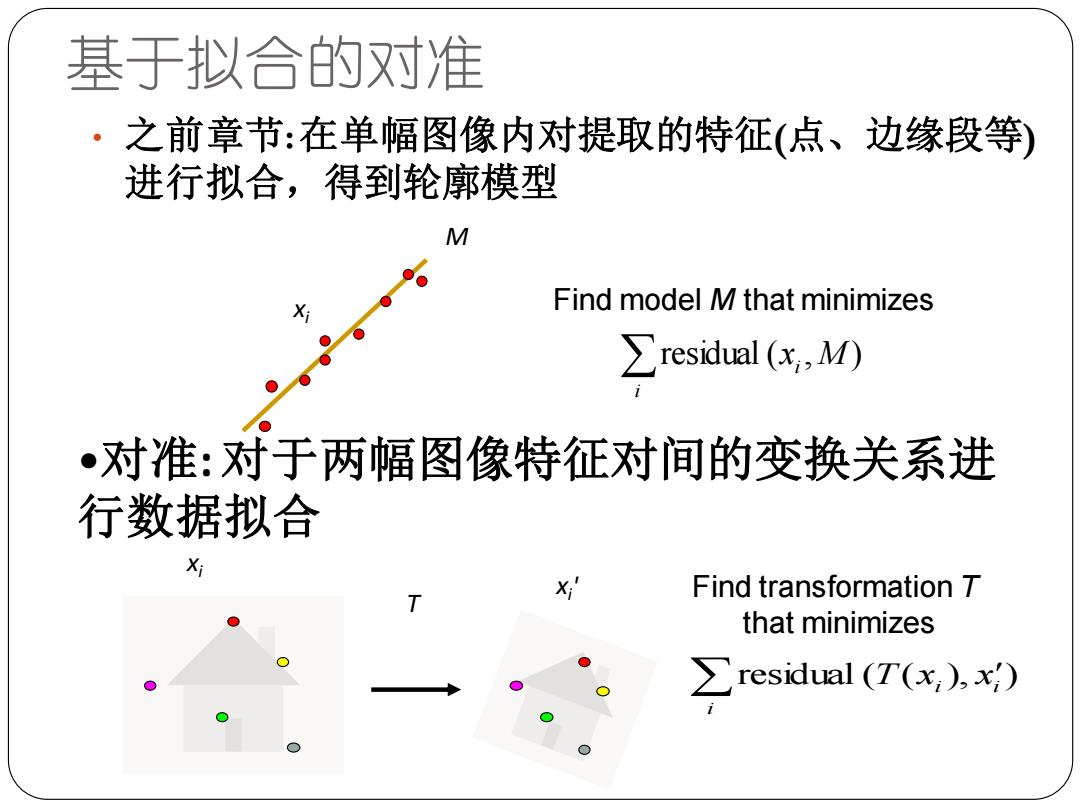
基于拟合的对准 。 之前章节:在单幅图像内对提取的特征(点、边缘段等) 进行拟合,得到轮廓模型 M Find model M that minimizes ∑residual(c,M) •对准:对于两幅图像特征对间的变换关系进 行数据拟合 X X Find transformation T that minimizes ∑residual(T(x),x)
基于拟合的对准 i residual (xi ,M ) • 之前章节: 在单幅图像内对提取的特征(点、边缘段等) 进行拟合,得到轮廓模型 Find model M that minimizes M xi •对准: 对于两幅图像特征对间的变换关系进 行数据拟合 i T xi xi residual ( ( ), ) Find transformation T that minimizes T xi xi
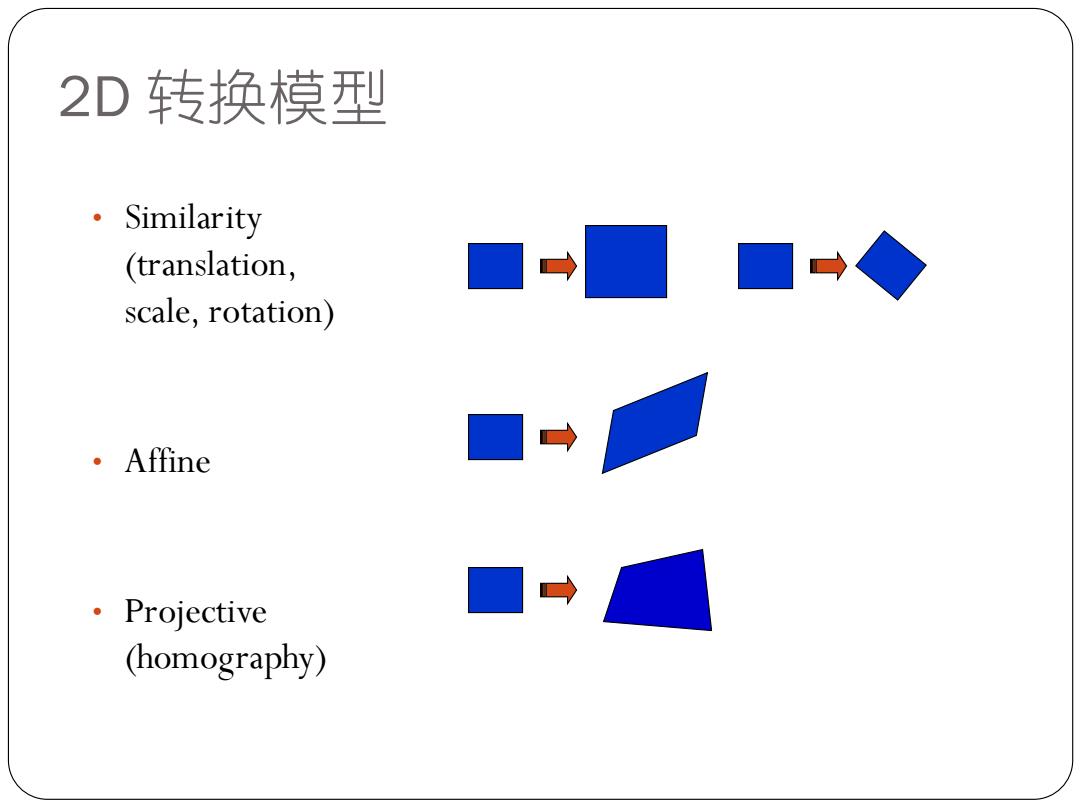
2D转换模型 Similarity (translation, ■→◆ scale,rotation) ·Affine ·Projective (homography)
2D 转换模型 • Similarity (translation, scale, rotation) • Affine • Projective (homography)

从仿射变换开始 简单的数据拟合程序(线性最小二乘法) 对于近似平面表面的物体和近似正交的相机可以近似 看作是视点变化 。 可以作为更复杂模型的初始拟合结果
从仿射变换开始 • 简单的数据拟合程序(线性最小二乘法) • 对于近似平面表面的物体和近似正交的相机可以近似 看作是视点变化 • 可以作为更复杂模型的初始拟合结果
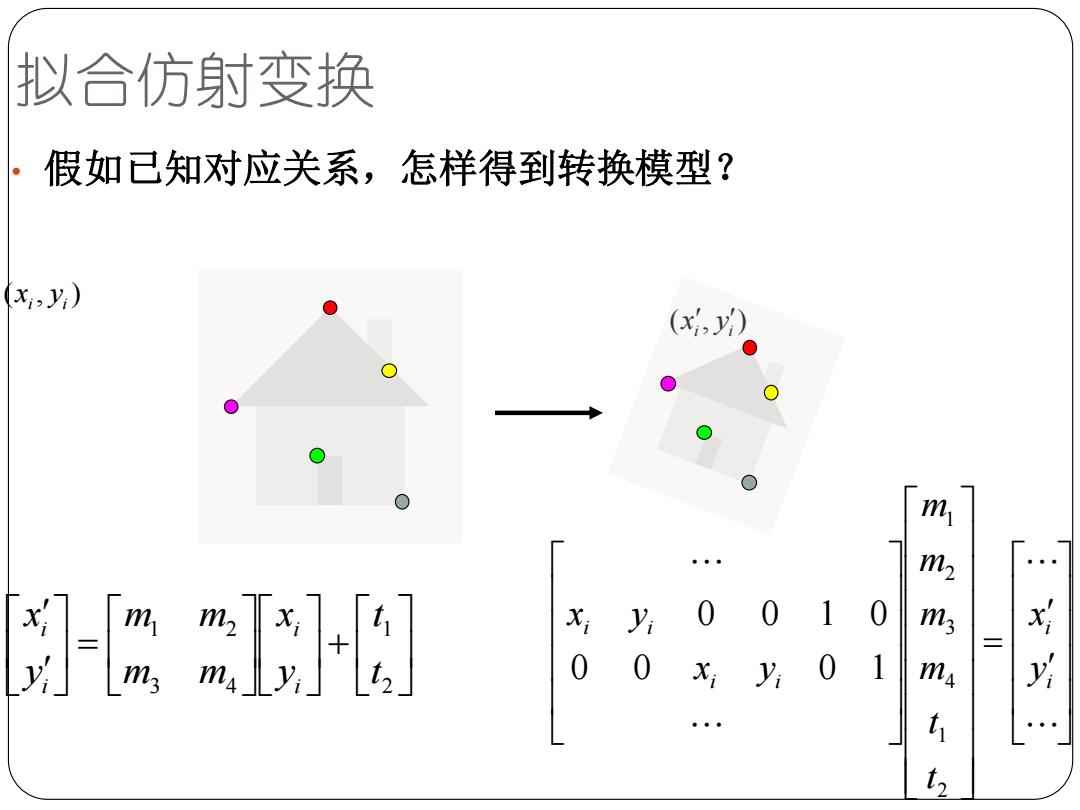
拟合仿射变换 ·假如已知对应关系,怎样得到转换模型? x,y) (x,) X y 0 0 10 0 0xy01
拟合仿射变换 ( , ) i i x y • 假如已知对应关系,怎样得到转换模型? ( , ) i i x y + = 2 1 3 4 1 2 t t y x m m m m y x i i i i = i i i i i i y x t t m m m m x y x y 2 1 4 3 2 1 0 0 0 1 0 0 1 0