
第十章基于立体视觉的深度估计
第十章 基于立体视觉的深度估计
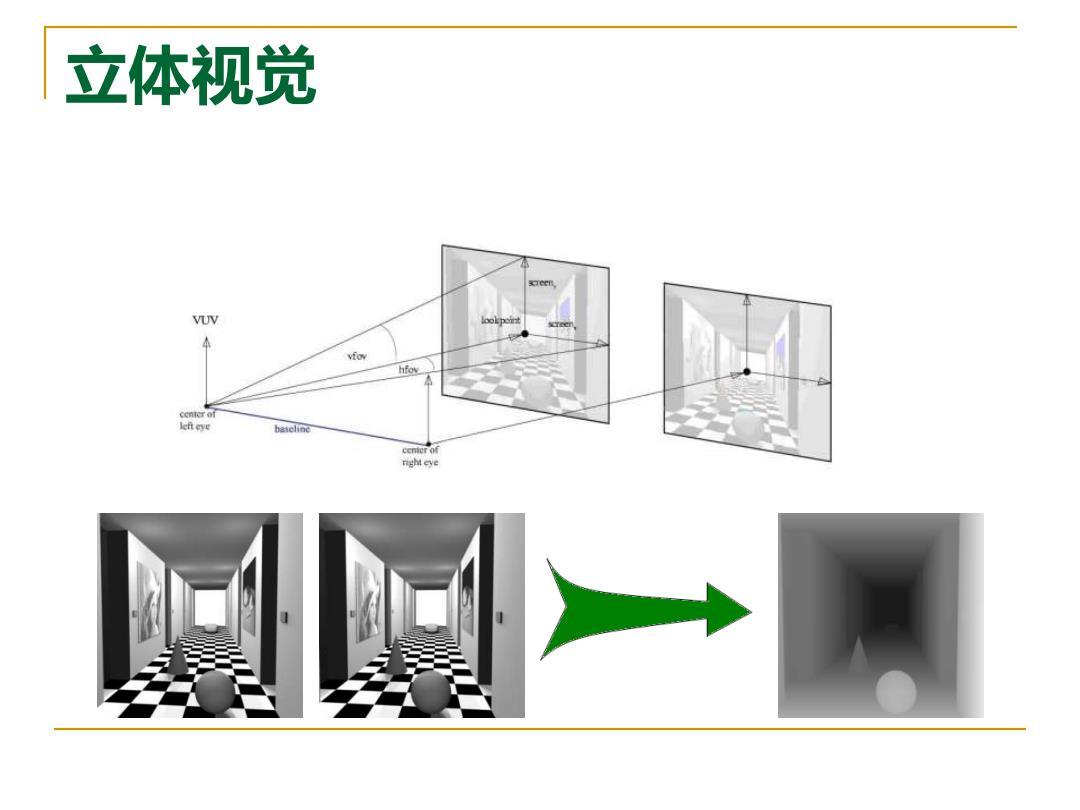
立体视觉 VUV left eye bateline center of right cye
立体视觉

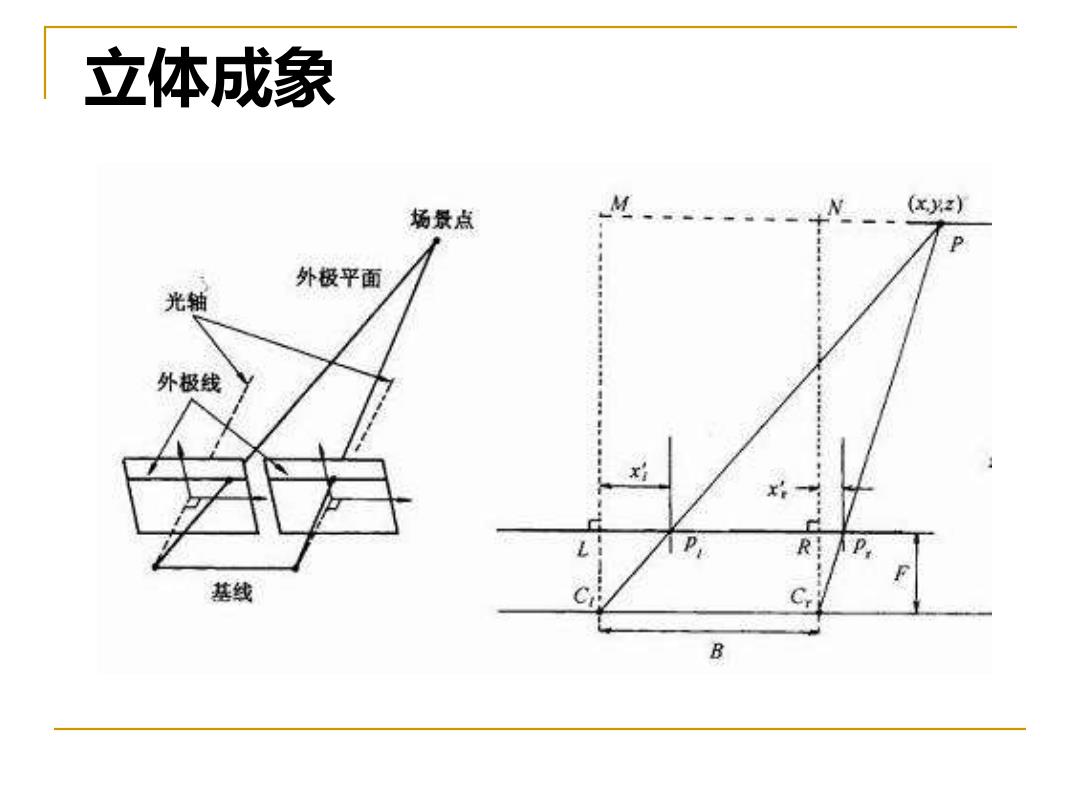
立体成象 我们将场景中同一点在两个不同图像中的投影 点称为共轭对 其中的一个投影点是另一个投影点的对应 (correspondence) 两幅图像重叠时的共轭对点的位置之差(共轭 对点之间的距离)称为视差(disparity) 通过两个摄像机中心并目通过场景特征点的平 面称为外极(epipolar))平面 外极平面与图像平面的交线称为外极线
立体成象 ◼ 我们将场景中同一点在两个不同图像中的投影 点称为共轭对 ◼ 其中的一个投影点是另一个投影点的对应 (correspondence) ◼ 两幅图像重叠时的共轭对点的位置之差(共轭 对点之间的距离)称为视差(disparity) ◼ 通过两个摄像机中心并且通过场景特征点的平 面称为外极(epipolar)平面 ◼ 外极平面与图像平面的交线称为外极线.
立体成象 场景点 (xz) P 外极平面 光轴 外极线 R 基线 B
立体成象

立体成象 由相似三角形可得 X-x x-B x Z 合并两项,可得 BF Z= xj-x F是焦距,B是基线距离
立体成象 F x z x l = F x z x B r = − l r x x BF z − = 由相似三角形可得 合并两项,可得 F是焦距,B是基线距离

立体成象 因此,各种场景点的深度恢复可以通过计算视差来实 现. 大角度立体方法—提高场景点深度计算精度的有 效途径 主要的问题有: 随着基线距离的增加,两个摄像机的共同的可视范 围减小 场景点对应的视差值增大,则搜索对应点的范围增 大,出现多义性的机会就增大 由透视投影引起的变形导致两个摄像机获取的两幅 图像中不完全相同,这就给确定共轭对带来困难
立体成象 ◼ 因此,各种场景点的深度恢复可以通过计算视差来实 现. ◼ 大角度立体方法 ——提高场景点深度计算精度的有 效途径 主要的问题有: 随着基线距离的增加,两个摄像机的共同的可视范 围减小 场景点对应的视差值增大,则搜索对应点的范围增 大,出现多义性的机会就增大. 由透视投影引起的变形导致两个摄像机获取的两幅 图像中不完全相同,这就给确定共轭对带来困难.
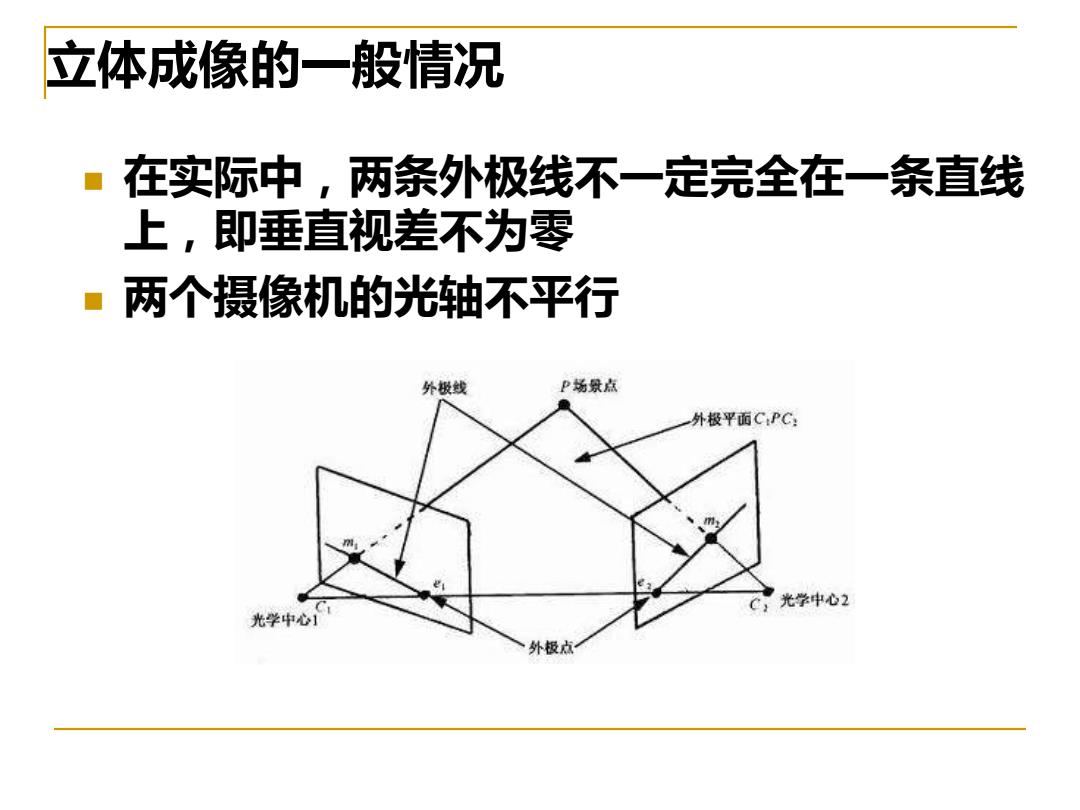
立体成像的一般情况 在实际中,两条外极线不一定完全在一条直线 上,即垂直视差不为零 两个摄像机的光轴不平行 外极线 P场景点 外极平面CPC C,光学中心2 光学中心1 外极点
立体成像的一般情况 ◼ 在实际中,两条外极线不一定完全在一条直线 上,即垂直视差不为零 ◼ 两个摄像机的光轴不平行
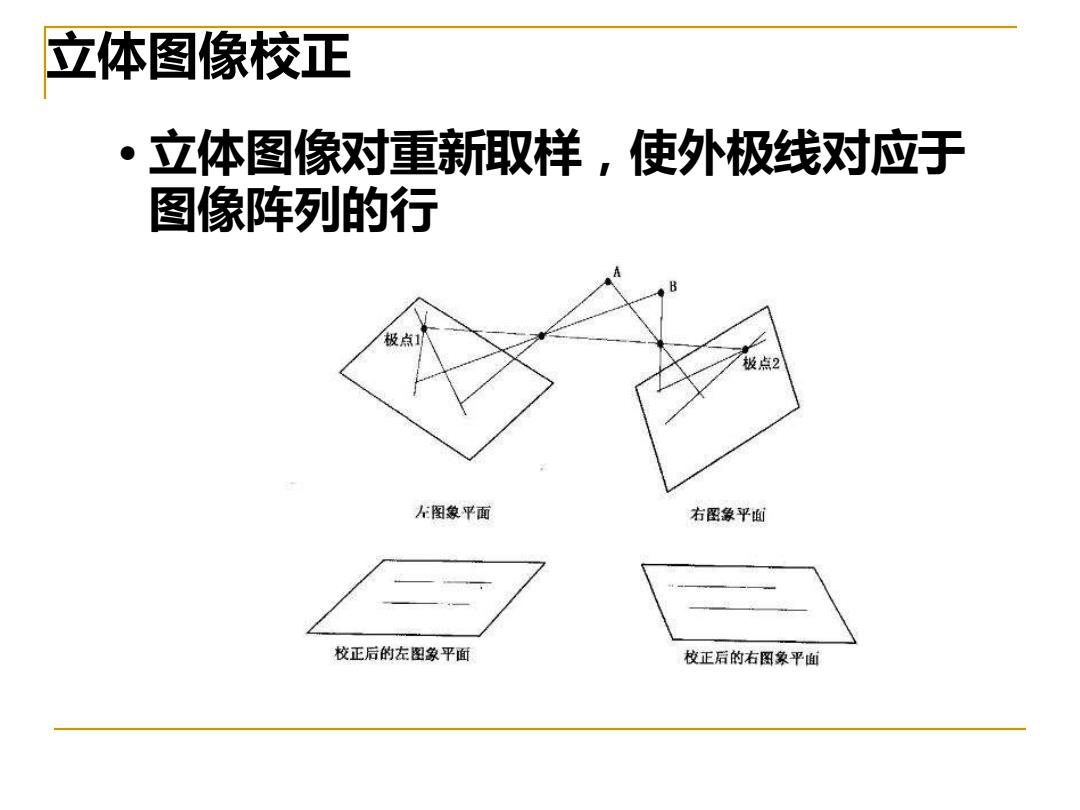
立体图像校正 立体图像对重新取样,使外极线对应于 图像阵列的行 极点1 极点2 左图象平面 右图象平面 校正后的左图象平面 校正后的右图象平面
立体图像校正 • 立体图像对重新取样,使外极线对应于 图像阵列的行

立体图像校正 将两图像投影到一个平面上就能得到理想的极线几 何.左(右)摄像机中的每一个像素点分别对应于左 (右)摄像机坐标系统中的一条射线。 设T和T分别表示将左、右摄像机的射线变换到公共 平面坐标系的刚体变换,确定每个图像的顶点在公共 平面上的位置,创建新的左、右图像网格,将每一个 网格点变换回原来的图像上·使用双变量线性内插方 法内插像素值可确定公共平面上新的左、右图像中的 像素点
立体图像校正 将两图像投影到一个平面上就能得到理想的极线几 何.左(右)摄像机中的每一个像素点分别对应于左 (右)摄像机坐标系统中的一条射线。 设Tl和Tr分别表示将左、右摄像机的射线变换到公共 平面坐标系的刚体变换,确定每个图像的顶点在公共 平面上的位置,创建新的左、右图像网格,将每一个 网格点变换回原来的图像上.使用双变量线性内插方 法内插像素值可确定公共平面上新的左、右图像中的 像素点
