
第之章 导数思想最早由法国 数学家Ferma在研究 导数与微分 极值问题中提出 微积分学的创始人: 英国数学家Newton 德国数学家Leibniz 导数 描述函数变化快慢 微分学 微分 描述函数变化程度 都是描述物质运动的工具(从微观上研究函数)
第二章 微积分学的创始人: 德国数学家 Leibniz 微分学 导数 描述函数变化快慢 微分 描述函数变化程度 都是描述物质运动的工具(从微观上研究函数) 导数与微分 导数思想最早由法国 数学家 Ferma 在研究 极值问题中提出. 英国数学家 Newton

第一节 第二章 导款的梳念 引例 二、导数的定义 三、导数的几何意义 四、函数的可导性与连续性的关系 五、单侧导数 HIGH EDUCATION PRESS 下页返回 结束
一、引例 二、导数的定义 三、导数的几何意义 四、函数的可导性与连续性的关系 五、单侧导数 第一节 机动 目录 上页 下页 返回 结束 导数的概念 第二章

一、 引例 1.变速直线运动的速度 设描述质点运动位置的函数为 s=f(t) 则to到t的平均速度为 f()-f(o) 自由落体运动 2 t-to 、=5gr2 而在1,时刻的瞬时速度为 f(to】 f()-f(t0) y lim 0 to t®to t-to HIGH EDUCATION PRESS 凯动 上页 反回
一、 引例 1. 变速直线运动的速度 设描述质点运动位置的函数为 则 到 的平均速度为 而在 时刻的瞬时速度为 自由落体运动 机动 目录 上页 下页 返回 结束

2.曲线的切线斜率 曲线C:y=f(x)在M点处的切线 y=f(x) 割线MN的极限位置MT (当7®a时) 切线MT的斜率 k tana lim tanj j®a 割线MN的斜率 tanj f()-f(xo) x-xo lim f(x)-f(xo) x®x0 x-xo HIGH EDUCATION PRESS 结束
2. 曲线的切线斜率 曲线 在 M 点处的切线 割线 M N 的极限位置 M T (当 时) 割线 M N 的斜率 切线 MT 的斜率 机动 目录 上页 下页 返回 结束

瞬时速度 y lim f(t)-f(to) t®to t-to 切线斜率k=1im f(x)-f() x®x0 x-Xo 两个问题的共性: 所求量为函数增量与自变量增量之比的极限 HIGH EDUCATION PRESS 下防 返回 结球
两个问题的共性: 瞬时速度 切线斜率 所求量为函数增量与自变量增量之比的极限 . 机动 目录 上页 下页 返回 结束

二、导数的定义 定义1.设函数y=f(x)在点x。的某邻域内有定义, 若 1m/(w-/xo)=1m D. Dy=f(x)-f(x) x®X0 x-xo Dx®OD Dx=x-xo 存在,则称函数(x)在点x处可导,并称此极限为 y=f(x)在点x的导数记作: y=;fx):】 v df(x) xx=xo dx x xo 即 y-o=fxo)=lim Dy x®ODX lim f(xo +Dx)-f(xo) lim f(xo +h)-f(xo) Dx®O Dx h®0 HIGH EDUCATION PRESS 返回 结
二、导数的定义 定义1 . 设函数 在点 存在, 并称此极限为 记作: 即 则称函数 若 的某邻域内有定义 , 在点 处可导, 在点 的导数. 机动 目录 上页 下页 返回 结束
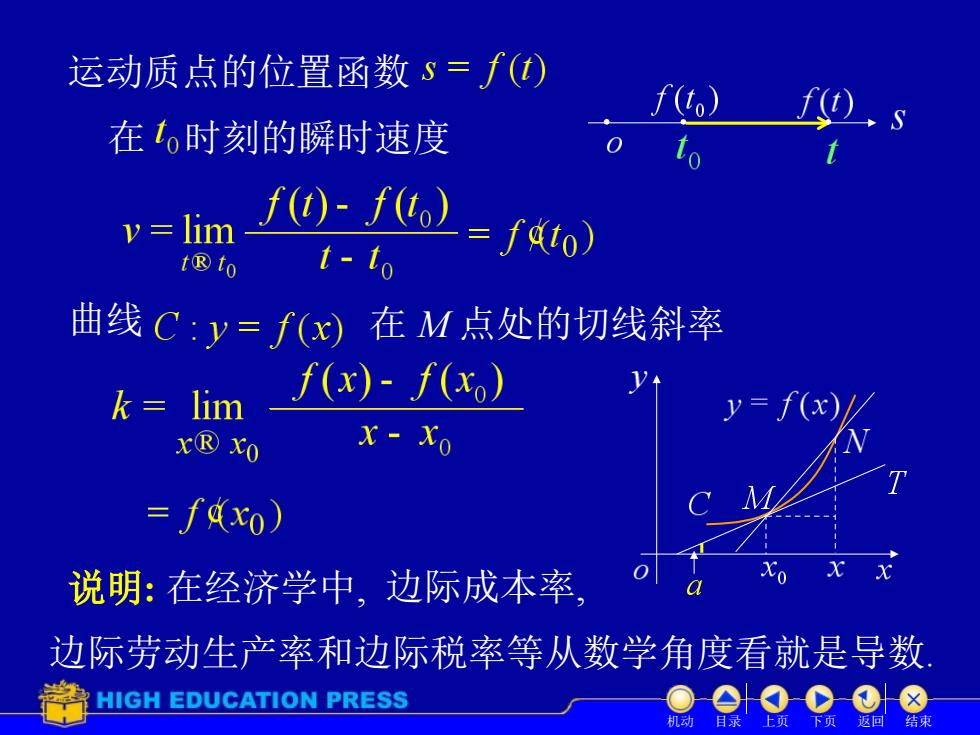
运动质点的位置函数s=f(t) f(t】 在1o时刻的瞬时速度 to y lim f0-f,)=fo) t®t0 t-to 曲线C:y=f(x) 在M点处的切线斜率 =lim- f(x)-f(x.) (x x®xo x-Xo =fdxo) 说明:在经济学中,边际成本率 边际劳动生产率和边际税率等从数学角度看就是导数 HIGH EDUCATION PRESS
运动质点的位置函数 在 时刻的瞬时速度 曲线 在 M 点处的切线斜率 说明: 在经济学中, 边际成本率, 边际劳动生产率和边际税率等从数学角度看就是导数. 机动 目录 上页 下页 返回 结束

lim f(x)-f(xo) =1m Dy Dy=f(x)-f(xo) x®X0 x-Xo Dx®ODX Dx=x-xo 若上述极限不存在,就说函数在点x不可导 若1m D=¥,也称∫)在的导数为无穷大 Dx®OD 若函数在开区间I内每点都可导,就称函数在I内可导. 此时导数值构成的函数称为导函数 记作:ygf知), dy.df(x) dx dx HIGH EDUCATION PRESS 目录
若上述极限不存在 , 在点 不可导. 若 也称 在 若函数在开区间 I 内每点都可导, 此时导数值构成的新函数称为导函数. 记作: 就说函数 就称函数在 I 内可导. 的导数为无穷大 . 机动 目录 上页 下页 返回 结束

例1.求函数f(x)=C(C为常数)的导数 解:w=im/e+D-fe=lm C-C 0 Dx®O Dx Dx®ODX 即 (C)2-0 例2.求函数f(x)=x”(miN)在=a处的导数 解:/ao)=1imf9-fa=1m ”-a” x®a x-a x®ax-a lim(x"-ax"-2+a2x"-3+L +a"l) x®a =nan-1 HIGH EDUCATION PRESS 结束
例1. 求函数 (C 为常数) 的导数. 解: 即 例2. 求函数 解: 机动 目录 上页 下页 返回 结束

说明: 对一般幂函数y=xm(m为常数) (x")=mx"I (利用第一章第九节例题7) 例a.5-g-台-3 (y-e-x1- -2 HIGH EDUCATION PRESS
说明: 对一般幂函数 ( 为常数) 例如, (利用第一章第九节例题7) 机动 目录 上页 下页 返回 结束