
第四节洛朗级数 一、问题的引入 二、洛朗级数的概念 三、函数的洛朗展开式 四、典型例题 五、小结与思考
第四节洛朗级数 二、洛朗级数的概念 一、问题的引入 三、函数的洛朗展开式 五、小结与思考 四、典型例题

一、问题的引入 在圆环域内解析的函数是否一定能展开成级数? 例如,fa)= 1 在z=0及z=1都不解析, z(1-z) 但在圆环域0<z<1及0<z-1<1内都是解析的. 在圆环域0<z<1内: (a)- 1 1,1 =z0-02+1-2 而 1=1+z+z2++z”+,z<1 1-
在圆环域 0 z 1内: 例如, 0 1 (1 ) 1 ( ) = = − = z z z z f z 在 及 都不解析, 但在圆环域 0 z 1 及 0 z − 1 1 内都是解析的. (1 ) 1 ( ) z z f z − = 而 1 , 1 1 1 2 = + + + + + − z z z z z n 在圆环域内解析的函数是否一定能展开成级数? , 1 1 1 z − z = + 2 一、问题的引入

所以f(z)= z(1-z) =z1+1+z+z2+.+z”+., 即f(z)在0<z<1内可以展开成级数, 在圆环域0<z-1<1内,也可以展开成级数: a02g[-】 =1+0-+0-++1-+ =(1-z)+1+(1-z)+(1-z)2+(1-z)”-1+
所以 (1 ) 1 ( ) z z f z − = 1 , = z −1 + + z + z 2 ++z n + 即 f (z)在 0 z 1 内可以展开成级数. 在圆环域0 z −1 1内, 也可以展开成级数: (1 ) 1 ( ) z z f z − = − − − = 1 (1 ) 1 1 1 z z + − + − ++ − + − = n z z z z 1 (1 ) (1 ) (1 ) 1 1 2 (1 ) 1 (1 ) (1 ) (1 ) . = − z −1 + + − z + − z 2 + − z n−1 +

00 2.双边幂级数∑cn(z-zo)” 觅ce-4r cn(z-zo) Cn(z-z)” n=」 1=-00 2=0 负幂项部分 正幂项部分 收敛 主要部分 解析部分 同时收敛
n n n 2. c (z z ) − 0 =− 双边幂级数 负幂项部分 正幂项部分 主要部分 解析部分 同时收敛 收敛 − = = =− n n n n c (z z ) 0 n n n n n n c (z z ) c (z z ) 0 0 0 1 − + − = − = − 4
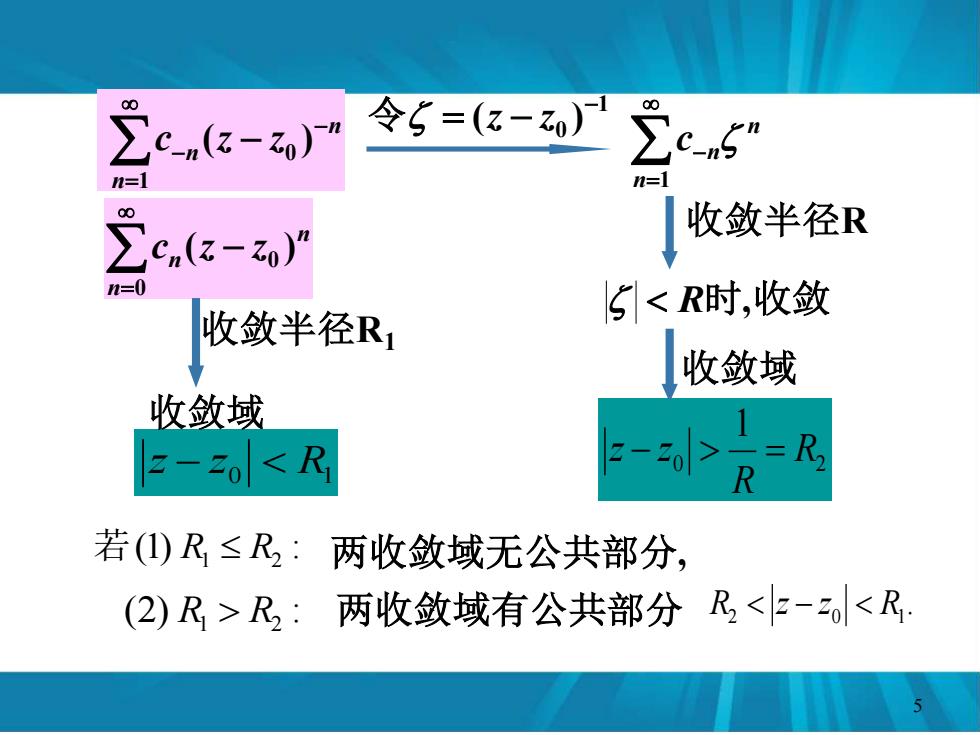
∑cn-) 令5=(z-0) 00 n=1 =1 00 收敛半径R Cn(z-z)” 1≥0 收敛半径R1 5R2:两收敛域有公共部分R<-<R
n n n c (z z ) 0 0 − = n n n c z z − = − ( − ) 0 1 1 0 ( ) − 令 = z − z n n n c = − 1 收敛半径R R时,收敛 0 2 1 R R z − z = 收敛域 收敛半径R1 0 R1 z − z 收敛域 (1) : 若 R1 R2 两收敛域无公共部分, (2) : R1 R2 两收敛域有公共部分 . 2 0 R1 R z − z 5
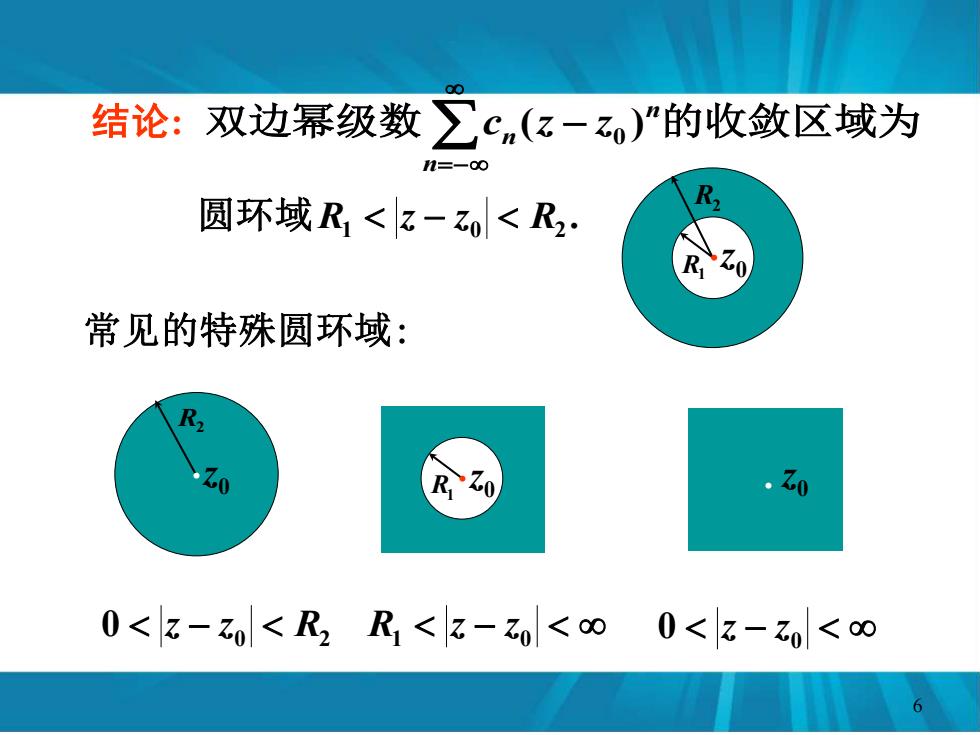
结论:双边幂级数 ∑cn(?-zo)”的收敛区域为 n=-00 圆环域R1<z-o<R2: 常见的特殊圆环域: R .0 0<z-z0<R2R1<z-z0<00<z-z0<0
结论: 双边幂级数 n的收敛区域为 n n c (z z ) − 0 =− . 1 0 R2 圆环域R z − z R1 R2 . 0 z 常见的特殊圆环域: R2 . 0 z 0 0 R2 z − z R1 . 0 z R1 z − z0 0 z − z0 . 0 z 6

定理4.11双边幂级数f(z)=∑cn(2-o)的收敛圆环 H:r<2-2o<R,(0≤r<R≤+o) 则(1)上述级数在H内绝对收敛并内闭一致收敛于 f(z)=f(z)+f,(z) (2)f(z)在H内解析 (3)fa)=∑c.(&-z)” -00 在H内可逐项求导,逐项求积分
定理4.11双边幂级数 的收敛圆环 + − = − n n f (z) c (z z )0 : ,(0 ) H r z − z0 R r R + 则(1)上述级数在H内绝对收敛并内闭一致收敛于 ( ) ( ) ( ) 1 2 f z = f z + f z (2) f (z)在H内解析 + − = − n n (3) f (z) c (z z ) 0 在H内可逐项求导,逐项求积分,. 7

二、洛朗级数 定理4.7洛朗定理 设f(z)在圆环域R<2-o<R,内处处解析, 那末f(z)在此圆环域内可展开成 ●● fz)=∑c(z-z), 脚。如gg为阴医改 (n=0,±1,.) C为圆环域内绕的任一正向简单闭曲线
二、洛朗级数 定理4.7洛朗定理 设 f (z)在圆环域R1 z − z0 R2 内处处解析, ( ) ( ) , 0 n n n f z = c z − z =− + − = C n n z f i c d ( ) ( ) 2π 1 1 0 其中 (n = 0, 1, ) C为圆环域内绕 0 的任一正向简单闭曲线. z 为洛朗系数. 那末 f (z)在此圆环域内可展开成 8

证明:在圆环域内作圆T5-=r和T25-o=R, 其中,R,<r<R<R,z是圆环域<5-zo<R内任意 一点,根据多连域的柯西积分公式有 e恩g 对于第一个积分,由于在工,上,点z在T的内部,所以 乙-z0 <1, 5-z0 又因为f(5)在T2上连续,因此存在一个正常数M, 使得f(5)<M,于是当5-o<R时可以得到
一点,根据多连域的柯西积分公式有 其中, 是圆环域 内任意 证明:在圆环域内作圆 : 和 : r R R z r z R z r z R − − = − = 2 0 1 0 2 0 , , 1 R d z f i d z f i f z − − − = 2 1 ( ) 2 ( ) 1 2 1 ( ) 对于第一个积分,由于在2 上,点z在2 的内部,所以 1, 0 0 − − z z z 使得 于是当 时可以得到 又因为 在 上连续,因此存在一个正常数 f M z R f M − 0 2 ( ) , ( ) , 9

十00 英e头=l2 考虑第二个积分,由于在工上,点z在工的外部,所以 1 于是 1=- 1 1 5-7 -1-5- (?-z)” 7-Z0 10
n n d c z z z f i ( ) ( ) 2 1 0 0 0 2 = − − + , 0,1,2, ( ) ( ) 2 1 2 1 0 = − = + d n z f i cn n 其中 考虑第二个积分,由于在1 上,点z在1 的外部,所以 1, 0 0 − − z z z 于是 = − − − = − − − − − = − − 1 0 1 0 0 0 0 ( ) ( ) 1 1 1 1 n n n z z z z z z z z z 10