
第一节共形映射的概念 一、几个相关的概念 二、解析函数导数的几何意义 三、共形映射的概念
第一节共形映射的概念 一、几个相关的概念 二、解析函数导数的几何意义 三、共形映射的概念

一、几个相关概念 z平面内的有向连续曲线C可表示为: z=z(t),(a≤t≤B) 正向:t增大时,点z移动的方向. 如果规定: ∠C 割线pop正向对应于t z(t+△t) 增大的方向,那么Po卫 与6+)-)同向. z(to) △t 0 2
2 z z(t), ( t ) 正向: t 增大时, 点 z 移动的方向. 如果规定: 割线 p p正向对应于 t 0 p p0 增大的方向 , 那么 . ( ) ( ) 与 0 0 同向 t z t t z t z平面内的有向连续曲线C可表示为: y 0 x C . . 0 p p ( ) 0 z t ( ) 0 z t t 一、几个相关概念

当p沿C,时, pp一C上P处切线 lim t→0 ,+A)-)=t)方向与C一致 △t 如果z'(t)≠0,a<t<B, )卫∠C (t+△t) 那么表示z'(t)的向量 z(to) 与C相切于点z=z(t):
3 ( ) ( ) ( ) lim 0 0 0 0 z t t z t t z t t 当 p , p0 时 p p0 C上 p0 处切线 ( ) 0, , 如果 z t0 t0 那么表示 z(t0 )的向量 ( ). 0 与C相切于点 z z t 方向与 C 一致. C . . 0 p p ( ) 0 z t ( ) 0 z t t ( ) 0 z t y 0 x 沿C

若规定z'()的方向(起点为z0)为C上点z0 处切线的正向,则有 1.切线倾角 Argz'(t)就是C上点z处的切线的正向与x轴 正向之间的夹角. 2'(to) Arg z'(to) Zo 0 4
4 0 0 0 若规定z(t )的方向(起点为z )为C上点z 处切线的正向, 则有 正向之间的夹角. Argz (t0 )就是C上点z0处的切线的正向与 x轴 C . 0 z y 0 x ( ) 0 z t Arg ( ) 0 z t 1.切线倾角
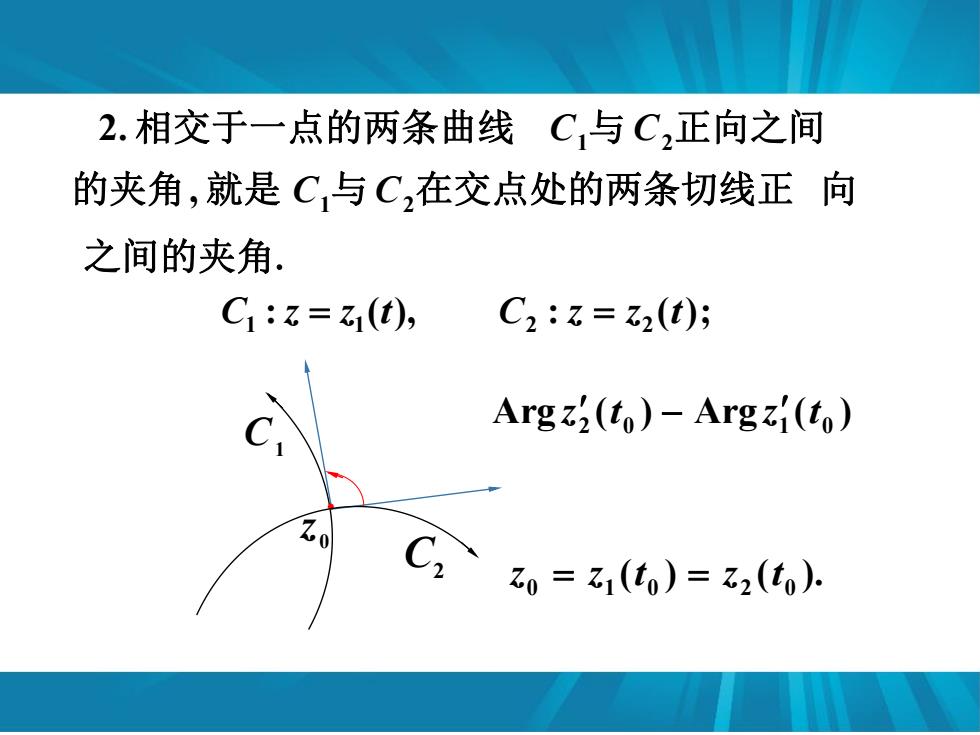
2.相交于一点的两条曲线C,与C,正向之间 的夹角,就是C与C,在交点处的两条切线正向 之间的夹角. C1:z=z1(t), C2:z=z2(t); Argz2(t)-Argz(t) z0=z1(t0)=z2(t0)
2. 相交于一点的两条曲线 C1与 C2正向之间 的夹角, 就是 C1与 C2在交点处的两条切线正 向 之间的夹角.: ( ), 1 1 C z z t : ( ); 2 2 C z z t C1 Arg ( ) Arg ( ) 2 0 1 0 z t z t . 0 z ( ) ( ). 0 1 0 2 0 z z t z t C2
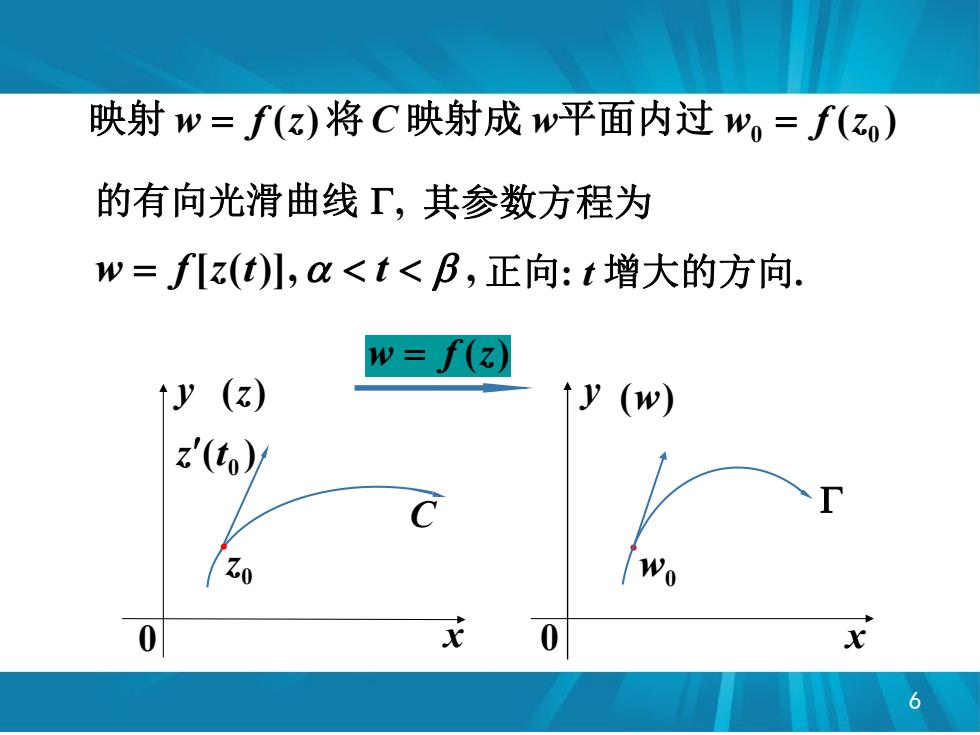
映射w=f(z)将C映射成w平面内过w,=f(z) 的有向光滑曲线Γ,其参数方程为 w=fz(t)川,a<t<B,正向:t增大的方向. w=f(z) 1y (z) ↑y(w) z'(to) r Zo Wo 0 0 x 6
6 的有向光滑曲线 , 其参数方程为 w f[z(t)], t , 正向: t 增大的方向. ( ) ( ) 0 0 映射 w f z 将 C 映射成 w平面内过 w f z C 0 z . y 0 x (z) ( ) 0 z t y 0 x (w) w0 . w f (z)
↑y( △S 0 0 w=f(z)↑y(w) △ R 0
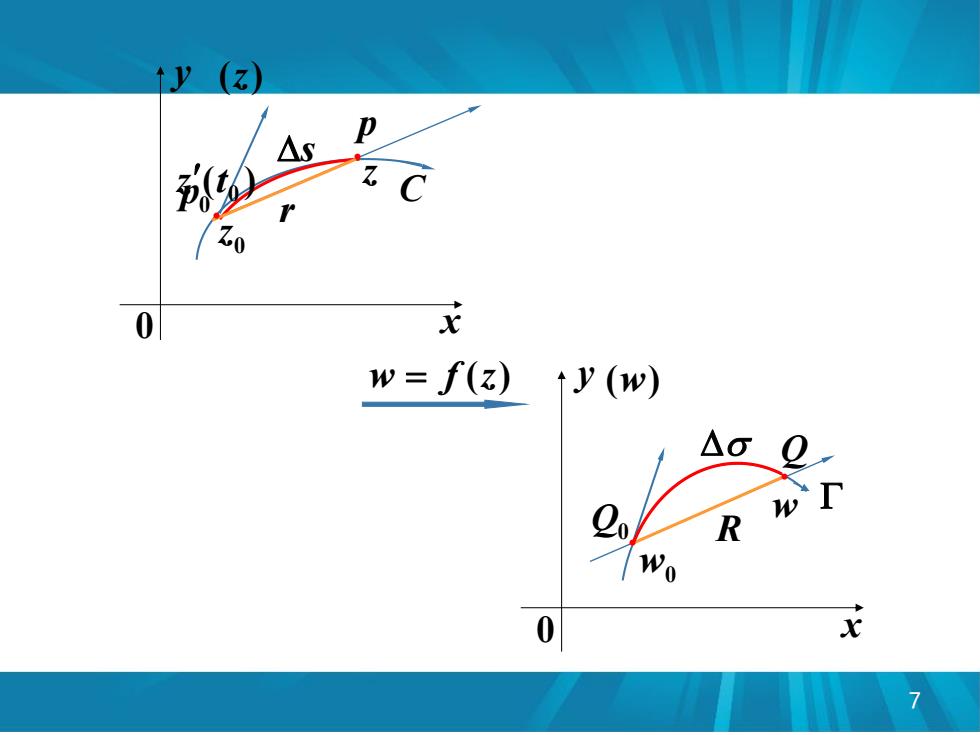
7 C y 0 x (w) y 0 x (z) s R ( ) 0 z t Q0 Q w0 w . . w f (z) r 0 p p 0 z z .

3.伸缩率 当z沿着曲线C趋向与z点时,如果lim w-wo存 z→20 z-20 在,则此极限值称为曲线C经函数w=f(z)映射后 在z处的伸缩率. 4.旋转角 设曲线C在z处的切线倾角为日,曲线厂在w处的 切线倾角为po,则p。-0,称曲线C经函数w=f(z) 映射后在z处的旋转角. 8
8 3.伸缩率 在 处的伸缩率. 在,则此极限值称为曲线 经函数 映射后 当 沿着曲线 趋向与 点时,如果 存 0 0 0 0 ( ) lim 0 z C w f z z z w w z C z z z 4.旋转角 映射后在 处的旋转角. 切线倾角为 则 称曲线 经函数 设曲线 在 处的切线倾角为 曲线 在 处的 0 0 0 0 0 0 0 , ( ) , z C w f z C z w

说明: 1.伸缩率和旋转角描述了在映射w=f(z)下,曲 线工相对与曲线C的变化特征, 2.当函数w=f(z)解析时,上述两个特征可以由导 数的模和辐角定量给出. 下面给出解析函数的导数的几何意义
9 说明: 线Γ相对与曲线C的变 化特征. 1.伸缩率和旋转角描 述了在映射 w f (z)下,曲 数的模和辐角定量给出 . 2.当函数w f (z)解析时,上述两个特征可以由导 下面给出解析函数的导 数的几何意义

二、导数的几何意义 1.导数的定义 f(zo)=lim f(z)-f(z)=lim -Wo →z0 7-Z0 2→z07-Z0 设函数w=f(z)在区域D内解析,乙∈D,并 且f(zo)≠0,则由导数的定义可得 10
10 二、导数的几何意义 1.导数的定义 0 0 0 0 0 ' 0 0 lim ( ) ( ) ( ) lim z z w w z z f z f z f z z z z z 且 则由导数的定义可得 设函数 在区域D内解析 并 , , ( ) 0 ( ) , 0 ' 0 f z w f z z D