
第5章有噪信道编码 第五章有噪信道编码 信息理论与编码 1
第五章 有噪信道编码 信息理论与编码 1 第5章 有噪信道编码

主要内容 1、译码规则对错误概率的影响 2、两种典型的译码规则 3、信道编码对平均差错率和信息率的影 咆 4、汉明距离 5、有噪信道编码定理(香农第二定理 6、有噪信道编码逆定理 7、线性分组码 第五章有噪信道编码 信息理论与编码 2
第五章 有噪信道编码 信息理论与编码 2 主要内容 1、译码规则对错误概率的影响 2、两种典型的译码规则 3、信道编码对平均差错率和信息率的影 响 4、汉明距离 5、有噪信道编码定理(香农第二定理) 6、有噪信道编码逆定理 7、线性分组码

实际信道由于信道噪声的干扰,传输 错误不可避免。为了降低平均差错率,可 先对消息进行编码— 信道编码,再送入 信道传送。 第五章有噪信道编码 信息理论与编码 3
第五章 有噪信道编码 信息理论与编码 3 实际信道由于信道噪声的干扰,传输 错误不可避免。为了降低平均差错率,可 先对消息进行编码——信道编码,再送入 信道传送

1、译码规则对错误概率的影响 译码是一种映射: F(b)=a,∈A,j=1,2,s 信道正好入的是4,=>正确译码 信道输入的不是☑,=>错误译码 译码正确概率 PX=aIY=b)=PLFb)川b,」 译码错误概率: P(elb)=P[X+F(b)IY=b]=1-P[F(b)b] 第五章有噪信道编码 信息理论与编码 A
第五章 有噪信道编码 信息理论与编码 4 1、译码规则对错误概率的影响 译码是一种映射: , 信道正好输入的是 =>正确译码 信道输入的不是 =>错误译码 译码正确概率: 译码错误概率: * ( ) F b a A j j j s 1, 2,... * aj * aj * ( | ) ( ) | P X a Y b P F b b j j j j ( | ) ( ) | 1 ( ) | P e b P X F b Y b P F b b j j j j j

平均差错率: P(P(eb,) 名 P(b){1-P[F(b,)Ib,]} = 1一 若P[F(b)b,] 或 -1->P[F(]P[b,IF(,] E=∑.Pa,b)=∑.Pa)Pbla) Y.X-a Y.X-a 好的译码规则应使平均差错率小。 第五章有噪信道编码 信息理论与编码 5
第五章 有噪信道编码 信息理论与编码 5 平均差错率: 或 好的译码规则应使平均差错率小。 1 1 ( ) ( | ) ( ) 1 ( ) | s e j j j s j j j j P P b P e b P b P F b b 1 1 1 ( ), 1 ( ) | ( ) s j j j s j j j j P F b b P F b P b F b * * , , ( , ) ( ) ( | ) e i j i j i Y X a Y X a P P a b P a P b a
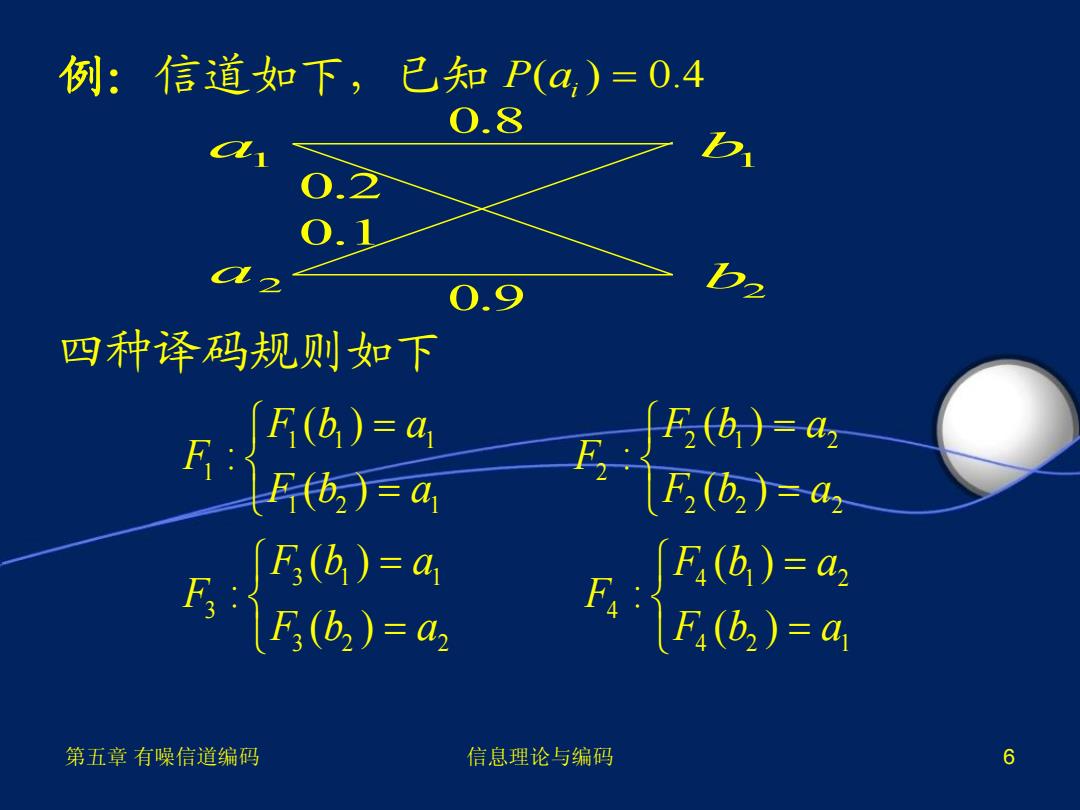
例:信道如下,已知P(a,)=0:4 0.8 0.1 0.9 四种译码规则如下 F F(b)=4 [F3(b)=az F(b2)=a F2(62)=az F (F;(b)=a [F(b)=a2 F3(b2)=az F4(b2)=4 第五章有噪信道编码 信息理论与编码 6
第五章 有噪信道编码 信息理论与编码 6 例:信道如下,已知 四种译码规则如下 P a( ) 0.4 i 0.8 0.9 0.2 0.1 b2 a1 b1 a2 1 1 1 2 1 2 1 2 1 2 1 2 2 2 3 1 1 4 1 2 3 4 3 2 2 4 2 1 ( ) ( ) : : ( ) ( ) ( ) ( ) : : ( ) ( ) F b a F b a F F F b a F b a F b a F b a F F F b a F b a

信道输入概率矩阵[P]=[0.40.6] 0.80.2 转移概率矩阵为]=0109 将Pa)乘以[Px]的第i行得联合概率矩阵 0.32 0.08 [2x1=0.06 0.54 译码规则:所对应的平均差错率为 P(F)=1->P[F(b),b] =1-[P(41,b)+P(41,b2)] =1-(0.32+0.08) 第五章有噪信道编码 0.6 信息理论与编码 7
第五章 有噪信道编码 信息理论与编码 7 信道输入概率矩阵 转移概率矩阵为 将 乘以 的第i行得联合概率矩阵 译码规则F1所对应的平均差错率为 [ ] 0.4 0.6 PX | 0.8 0.2 [ ] 0.1 0.9 PY X i P( a ) | [ ] PY X 0.32 0.08 [ ] 0.06 0.54 PXY 1 1 1 1 1 1 2 ( ) 1 ( ), 1 ( , ) ( , ) 1 (0.32 0.08) 0.6 s e j j j P F P F b b P a b P a b

同理,其它几种译码规则对应的 平均差错率分别为 P(F2)=0.4 P(F3)=0.14 P(F4)=O.86 4种规则相比,F3最好,F4最差。 0分 第五章有噪信道编码 信息理论与编码 8
第五章 有噪信道编码 信息理论与编码 8 同理,其它几种译码规则对应的 平均差错率分别为 4种规则相比,F3最好,F4最差。 2 3 4 ( ) 0.4 ( ) 0.14 ( ) 0.86 e e e P F P F P F

2、两种典型的译码规则 (1)最佳译码规则 使P。达到最小的译码规则 最佳译码规则的确定: 计算出所有以b,为条件的输入符号的 概率,即后验概率: {P(a b),P(ab)..P(a,b,) 取最大后验概率所对应的输入符号为 译码输出a,F6,)=0r Fb,)=aeA,b,∈B 即 Pa,1b)2Pa,Ib,),a∈A 又称最大后验概率译码规则 第五章有噪信道编码 信息理论与编码 9
第五章 有噪信道编码 信息理论与编码 9 2、两种典型的译码规则 (1)最佳译码规则 使 达到最小的译码规则 最佳译码规则的确定: 计算出所有以 为条件的输入符号的 概率,即后验概率: 取最大后验概率所对应的输入符号为 译码输出 , 。 即 又称最大后验概率译码规则。 P e j b 1 2 { ( | ), ( | ), , ( | )} P a b P a b P a b j j r j * j a * ( ) F b a j j * * ( ) , : ( | ) ( | ) , j j j j j i j i F b a A b B F P a b P a b a A

最大后验概率条件可等价成最大联合概 率条件 P(a1b,)≥P(a,Ib,) P(b)P(a,Ib)2 P(b)P(a,b) Pa,b,)≥P(a,b,) 最佳译码规则又可表示成: F(t)=a,∈A,b,∈B P(a,b,)≥P(a,b,),a,∈A 因此,该规则又称为最大联合概率译码 规则。 第五章有噪信道编码 信息理论与编码 10
第五章 有噪信道编码 信息理论与编码 10 最大后验概率条件可等价成最大联合概 率条件 最佳译码规则又可表示成: 因此,该规则又称为最大联合概率译码 规则。 * * * ( | ) ( | ) ( ) ( | ) ( ) ( | ) ( , ( , ) j j i j j j j j i j j j i j P a b P a b P b P a b P b P a b P a b P a b * * ( ) , : ( , ) ( , ) , j j j j j i j i F b a A b B F P a b P a b a A