
第6章限失真信源编码 2010年7月21日1时3分 信息理论与编码 1
2010年7月21日1时3分 信息理论与编码 1 第6章 限失真信源编码

主要内容 1、有失真编码的目的 2、采用限失真编码的原因 3、失真测度 4、信息率失真函数及其性质 5、限失真信源编码定理 第六章限失真信源编码 信息理论与编码 2
第六章 限失真信源编码 信息理论与编码 2 主要内容 1、有失真编码的目的 2、采用限失真编码的原因 3、失真测度 4、信息率失真函数及其性质 5、限失真信源编码定理

1、有失真编码的目的 在允许的失真范围内把编码后的信息 率压缩到最小。如果限定失真范围,又称 为限失真编码,编码后的信,息率得到压缩」 2、采用限失真编码的原因 1)保熵编码并非总是必需的。 2)保熵编码并非总是可能的。 3)可降低信,息率有利于传输和处理。 第六章限失真信源编码 信息理论与编码
第六章 限失真信源编码 信息理论与编码 3 1、有失真编码的目的 在允许的失真范围内把编码后的信息 率压缩到最小。如果限定失真范围,又称 为限失真编码,编码后的信息率得到压缩。 2、采用限失真编码的原因 1)保熵编码并非总是必需的。 2)保熵编码并非总是可能的。 3)可降低信息率有利于传输和处理

3、失真测度 设信源为U={442,…,u,},信源编码后 的输出V={,V2,…,V}。编码器输入符号与输 出符号之间的误差或失真可用一个非负实 值函数一失真度(或失真函数)d(4,v,) 来描述。将rXS个d(4,v,排成矩阵形式 称为失真矩阵,记为d]: V2 d(4,y) d(4,v2) d(u,v,) 241 [d]= d(42,) d(42,y2)…d(42,v) 42 d(4,y)d(4n,2) d(u,,vs)] u, 第六章限失真信源编码 信息理论与编码 4
第六章 限失真信源编码 信息理论与编码 4 3、失真测度 设信源为U= ,信源编码后 的输出V= 。编码器输入符号与输 出符号之间的误差或失真可用一个非负实 值函数——失真度(或失真函数) 来描述。将 个 排成矩阵形式, 称为失真矩阵,记为 : 1 2 1 1 1 2 1 1 2 1 2 2 2 2 1 2 ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) [ ] ( , ) ( , ) ( , ) s s s r r r s r v v v d u v d u v d u v u d u v d u v d u v u d d u v d u v d u v u 1 2 { , , , }r u u u 1 2 { , , , }s v v v ( , ) i j d u v r s ( , ) i j d u v [ ] d

对所有符号的失真度{4,y)取统计 平均,称为平均失真度或平均失真,记万 D=E{d4,y}=∑∑P4,y)d(4,y) i=1j=1 -∑ΣPa,)P℃,4,du,y,) i=1 i=l 要求失真度d(4,y,)20,常用的失真度有: 误码失真: 0,4=y 均方失真: duv))=,4y d4,v,)=(4,-Y,) 绝对失真: 相对失真: d(4,v,)=4,-yl d(u,y)=4-y/4 第六章限失真信源编码 信息理论与编码 5
第六章 限失真信源编码 信息理论与编码 5 对所有符号的失真度 取统计 平均,称为平均失真度或平均失真,记 要求失真度 ,常用的失真度有: 误码失真: 均方失真: 绝对失真: 相对失真: , ( , ) i j i j d u v D 1 1 1 1 ( , ) ( , ) ( , ) ( ) ( | ) ( , ) r s i j i j i j i j r s i j i i j i j D E d u v P u v d u v P u P v u d u v ( , ) 0 i j d u v 0 , ( , ) 1 , i j i j i j u v d u v u v 2 ( , ) ( ) d u v u v i j i j ( , ) | | i j i j d u v u v ( , ) | | | | i j i j i d u v u v u

对于符号序列,可将失真度或失真函 数的定义可推广到矢量形式。设编码器输 入C和输出B,均为N长符号序列,即 Cn=LmLh·LnN h=1,2,,rN 1=1,2,…,sN 则N长符号序列的失真度d(a,B,)可定义 为 平均失真度为DNM=E{d(a,A}=∑∑Pa,B,)d(a,B)》 h=1l= 2aAa飞 第六章限失真信源编码 信息理论与编码
第六章 限失真信源编码 信息理论与编码 6 对于符号序列,可将失真度或失真函 数的定义可推广到矢量形式。设编码器输 入 和输出 均为N长符号序列,即 则N长符号序列的失真度 可定义 为 平均失真度为 h l 1 2 1 2 1, 2, , 1, 2, , N N N h h h h N l l l l u u u h r v v v l s ( , ) h l d 1 ( , ) ( , ) k k N h l h l k d d u v 1 1 1 1 1 ( ) ( , ) ( , ) ( , ) ( , ) ( , ) N N N N k k r s h l h l h l h l r s N h l h l h l k D N E d P d P d u v

4、信息率失真函数及其性质 1)定义 如果要求平均失真万小于某个给定 值D,即要求 D=F{da,y}=∑∑Pu)Py4)d,y)≤D 限制条件称为保真度准则。 并非所有的信道能满足保真度准则 满足保真度准则 D的信道称为试验信 道。在所有试验信道中寻求一个 (配寻 求一个特定的编码器)使 最小)这个 最小的平均互信息量称为信息率失真函数, 简称为率失真函数,记为 R(D) 第六章限失真信源编码 信息理论与编码
第六章 限失真信源编码 信息理论与编码 7 4、信息率失真函数及其性质 1)定义 如果要求平均失真 小于某个给定 值 ,即要求 限制条件称为保真度准则。 并非所有的信道都能满足保真度准则, 满足保真度准则 的信道称为试验信 道。在所有试验信道中寻求一个 (即寻 求一个特定的编码器)使 最小,这个 最小的平均互信息量称为信息率失真函数, 简称为率失真函数,记为 D D 1 1 ( , ) ( ) ( | ) ( , ) r s i j i j i i j i j D E d u v P u P v u d u v D D D PV U| I U V ( ; )R D( )

即 RD)=min{IU,门,D≤Dy 当最小值不存在时,可用下界值代替: R(D)=inf I(U;) RIU∈BD 对于离散信源,可表示成 R(D)=min ∑∑PP也,4)log Pv,4) B∈Bp 1j1 P(v R(D)是保真度准则(D≤D)下所必须 传输的信,息率,也是熵压缩编码器输出可能 达到的最低熵率 第六章限失真信源编码 信息理论与编码 8
第六章 限失真信源编码 信息理论与编码 8 即 当最小值不存在时,可用下界值代替: 对于离散信源,可表示成 是保真度准则( )下所必须 传输的信息率,也是熵压缩编码器输出可能 达到的最低熵率。 R D I U V D D ( ) min ( ; ); | ( ) inf ( ; ) P B V U D R D I U V | 1 1 ( | ) ( ) min ( ) ( | )log V U D ( ) r s j i i j i P B i j j P v u R D P u P v u P v R D( ) D D
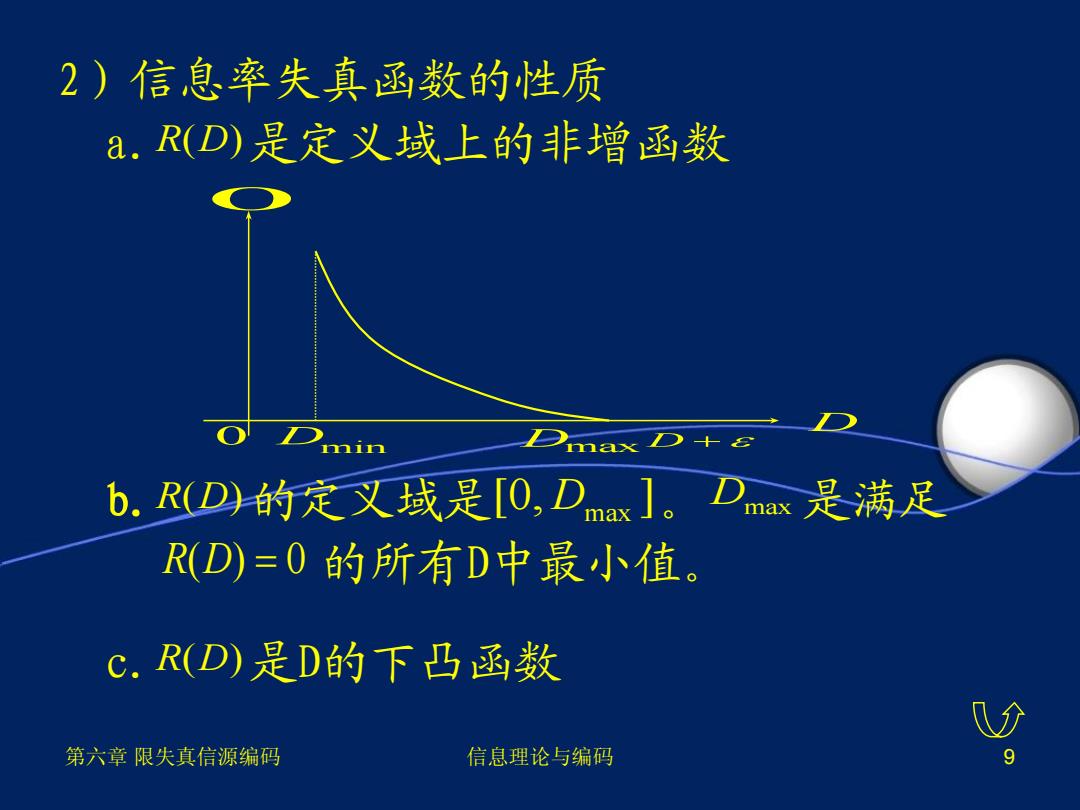
2)信息率失真函数的性质 a.R(D)是定义域上的非增函数 min max )十 b.R(D)的定义域是[O,Dmax]。 Dmax是满足 R(D)=0的所有D中最小值。 C.R(D)是D的下凸函数 第六章限失真信源编码 信息理论与编码 9
第六章 限失真信源编码 信息理论与编码 9 2)信息率失真函数的性质 a. 是定义域上的非增函数 b. 的定义域是 。 是满足 的所有D中最小值。 c. 是D的下凸函数 0 D 0 Dmin DmaxD R D( ) max R D( ) [0, ] D Dmax R D( ) 0 R D( )

5、限失真信源编码定理 香农第三定理设离散无记忆平稳信 源的信息率失真函数为R(D),只要满足R>(D) 当信源序列足够长时,一定存在一种编码 方法,其译码失真小于或等于D+,其中8 是任意小的正数;反过来,若R<R(D) 则无论采用什么样的编码方法,其译码失 真必大于D 该定理与香农第二编码定理一样,只 是码的存在性定理。迄今为止,尚无合适 的系统编码方法来接近香农给出的界R(D) 第六章限失真信源编码 信息理论与编码
第六章 限失真信源编码 信息理论与编码 10 5、限失真信源编码定理 香农第三定理 设离散无记忆平稳信 源的信息率失真函数为 ,只要满足 当信源序列足够长时,一定存在一种编码 方法,其译码失真小于或等于 ,其中 是任意小的正数;反过来,若 , 则无论采用什么样的编码方法,其译码失 真必大于 。 该定理与香农第二编码定理一样,只 是码的存在性定理。迄今为止,尚无合适 的系统编码方法来接近香农给出的界 。 R D( ) R R D ( ) D R R D ( ) D R D( )