
第4章离散无记忆信源无失真 编码 2010年7月21日1时4分 信息理论与编码 1
2010年7月21日1时4分 信息理论与编码 1 第4章 离散无记忆信源无失真 编码

主要内容 1、基本概念 2、码的唯一可译性 3、定长编码定理和定长编码方法 4、变长编码定理 5变长编码方法 6几种实用的无失真信源编码 第四章离散无记忆信源 信息理论与编码 2 无失真编码
第四章 离散无记忆信源 无失真编码 信息理论与编码 2 主要内容 1、基本概念 2、码的唯一可译性 3、定长编码定理和定长编码方法 4、变长编码定理 5 变长编码方法 6 几种实用的无失真信源编码

1、基本概念 信源发出的消息序列通常不能直接送 给信道传输,需要经过信源编码和信道编 码。 信道编码的目的是降低差错率,提高 传送的可靠性。 信源编码的目的是为了降低冗余度 提高通信的有效性 编码是一种映射,是将输入符号映射 成码字。无失真编码,映射一一对应,可 逆 第四章离散无记忆信源 信息理论与编码 3 无失真编码
第四章 离散无记忆信源 无失真编码 信息理论与编码 3 1、基本概念 信源发出的消息序列通常不能直接送 给信道传输,需要经过信源编码和信道编 码。 信道编码的目的是降低差错率,提高 传送的可靠性。 信源编码的目的是为了降低冗余度, 提高通信的有效性。 编码是一种映射,是将输入符号映射 成码字。无失真编码,映射一一对应,可 逆
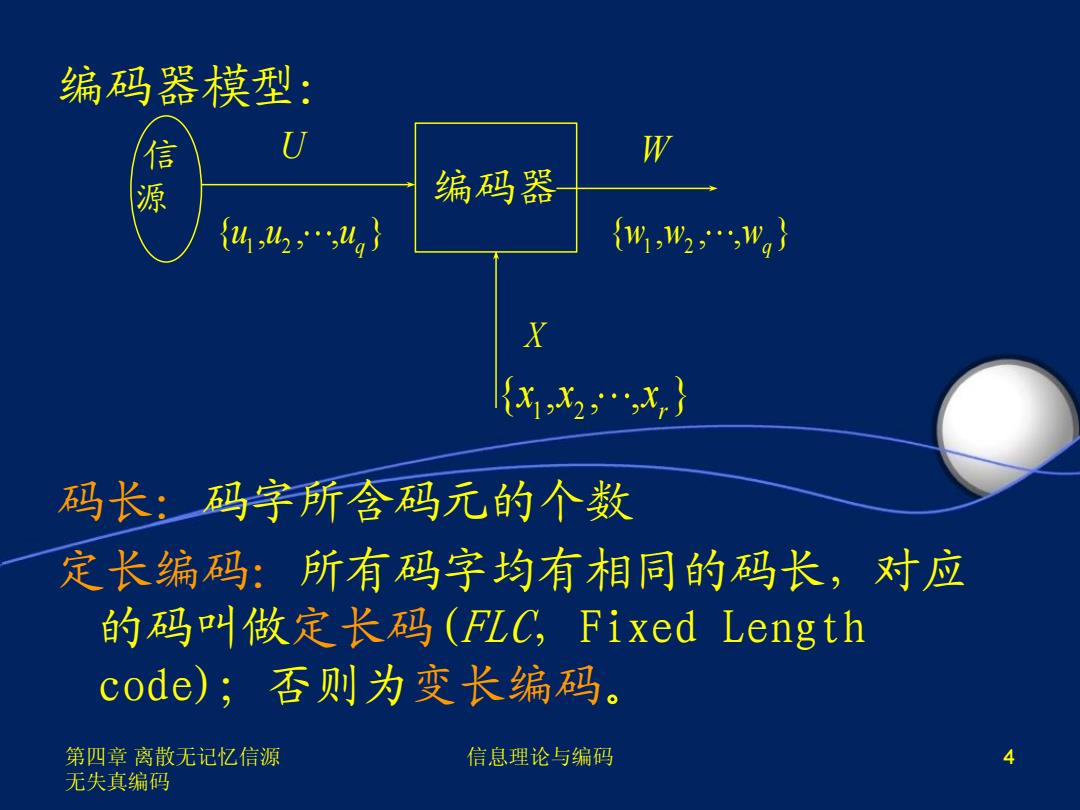
编码器模型: 信 W 源 编码器 4,42,,2g} {w02…,wg} X {x12,X,} 码长:码字所含码元的个数 定长编码:所有码字均有相同的码长,对应 的码叫做定长码(FLC,Fixed Length code);否则为变长编码。 第四章离散无记忆信源 信息理论与编码 4 无失真编码
第四章 离散无记忆信源 无失真编码 信息理论与编码 4 编码器模型: 码长:码字所含码元的个数 定长编码:所有码字均有相同的码长,对应 的码叫做定长码(FLC,Fixed Length code);否则为变长编码。 编码器 1 2 { , , , }q u u u 1 2 { , , , }r x x x U W 1 2 { , , , } w w wq X 信 源
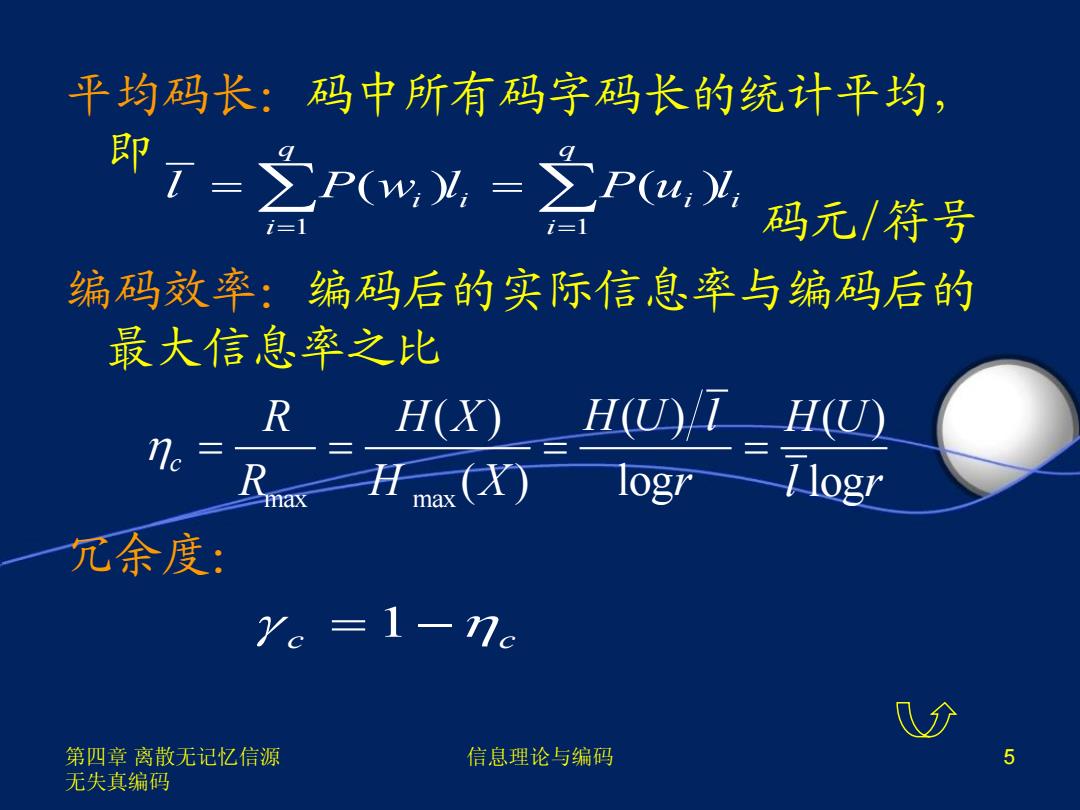
平均码长:码中所有码字码长的统计平均, 即7-之Pw为-之PU,Y 码元/符号 编码效率:编码后的实际信息率与编码后的 最大信息率之比 R H(X)H(U)T H(U) max 0X logr llogr 冗余度: Ye =1-nc 第四章离散无记忆信源 信息理论与编码 5 无失真编码
第四章 离散无记忆信源 无失真编码 信息理论与编码 5 平均码长:码中所有码字码长的统计平均, 即 码元/符号 编码效率:编码后的实际信息率与编码后的 最大信息率之比 冗余度: 1 1 ( ) ( ) q q i i i i i i l P w l P u l max max ( ) ( ) ( ) ( ) log log c R H X H U H U l R H X r l r c c 1

2、码的唯一可译性 (1)基本概念 奇异码:一组码中含相同码字 非奇异码:所有的码字都不相同 唯一可译性:码字组成的任意有限长码字序 列都能恢复成唯一的信源序列 续长码:有些码字是在另一些码字后 面添加码元得来的 及时码:码字的最后一个码元出现时,译码 器能立即判断一个码字已经结束,可以立 即译码 非续长码:任一码字都不是其它码字的延长。 第四章离散无记忆信源 信息理论与编码 6 无失真编码
第四章 离散无记忆信源 无失真编码 信息理论与编码 6 2、码的唯一可译性 (1)基本概念 奇异码:一组码中含相同码字。 非奇异码:所有的码字都不相同。 唯一可译性:码字组成的任意有限长码字序 列都能恢复成唯一的信源序列。 续长码:有些码字是在另一些码字后 面添加码元得来的。 及时码:码字的最后一个码元出现时,译码 器能立即判断一个码字已经结束,可以立 即译码。 非续长码:任一码字都不是其它码字的延长
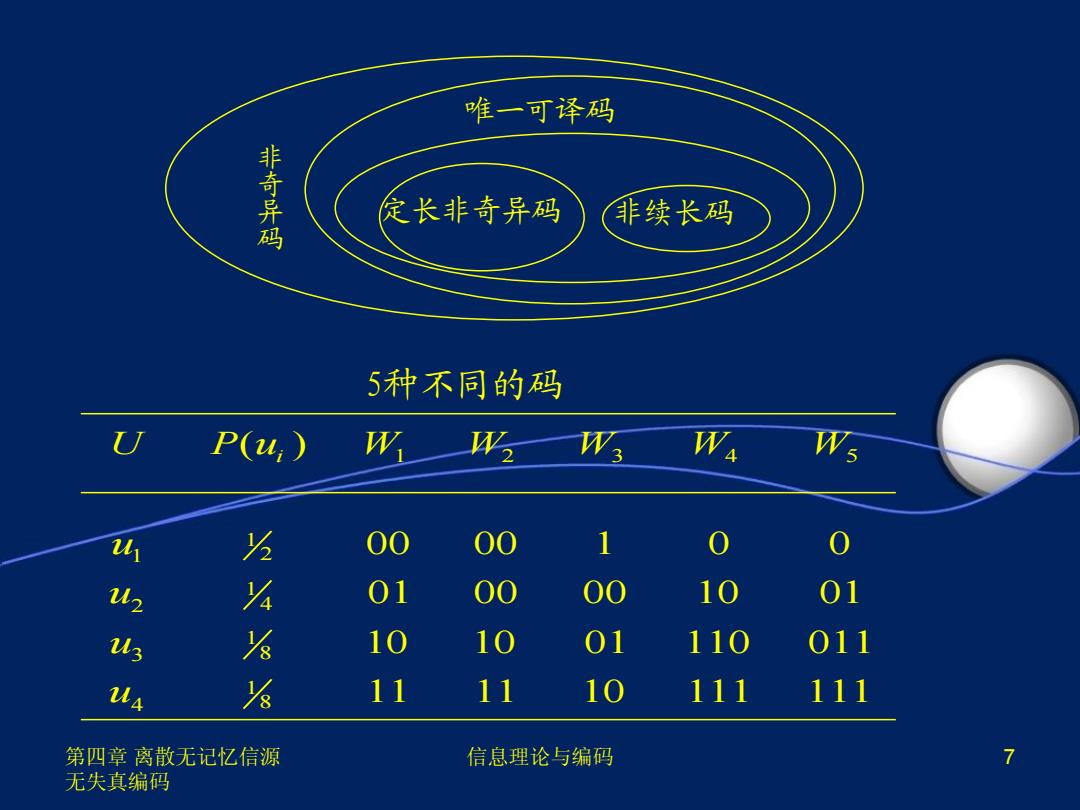
唯一可译码 非奇异码 定长非奇异码 非续长码 5种不同的码 U P(4,) W W2 W3 Wa Ws 为 00 00 1 0 % 01 00 00 10 01 u3 ⅓ 10 10 01 110 011 Us 名 11 11 10 111 111 第四章离散无记忆信源 信息理论与编码 7 无失真编码
第四章 离散无记忆信源 无失真编码 信息理论与编码 7 唯一可译码 定长非奇异码 非续长码 非 奇 异 码 5种不同的码 1 2 4 3 5 1 1 2 1 2 4 1 3 8 1 4 8 ( ) 00 00 1 0 0 01 00 00 10 01 10 10 01 110 011 11 11 10 111 111 U P u W W i W W W u u u u

(2)码树和Kraft不等式 从树根开始,生长r个树枝,在节点处 再各自生长r个树枝。 节点:树枝与树枝的交点。 1阶节,点:经过1根树枝到达的节,点。 整树:节点长出的树枝数等于工 定理:对于任一ǐ进制非续长码,各码 字的码长必须满足Kraft不等式:∑r≤1 反过来,若上式成立,就一定能构造一个ǐ 进制非续长码。 第四章离散无记忆信源 信息理论与编码 8 无失真编码
第四章 离散无记忆信源 无失真编码 信息理论与编码 8 (2)码树和Kraft不等式 从树根开始,生长r个树枝,在节点处 再各自生长r个树枝。 节点:树枝与树枝的交点。 l阶节点:经过l根树枝到达的节点。 整树:节点长出的树枝数等于r 定理:对于任一r进制非续长码,各码 字的码长必须满足Kraft不等式: 反过来,若上式成立,就一定能构造一个r 进制非续长码。 1 1 i q l i r

定理 对于任一进制唯一可译码 (UDC),各码字的码长必须满足Kraft不 等式: 之x4 ≤1 反过来,若上式成立,就一定能构造 一个进制唯一可译码(UDC) 第四章离散无记忆信源 信息理论与编码 9 无失真编码
第四章 离散无记忆信源 无失真编码 信息理论与编码 9 定理 对于任一进制唯一可译码 (UDC),各码字的码长必须满足Kraft不 等式: 反过来,若上式成立,就一定能构造 一个进制唯一可译码(UDC)。 1 i 1 q l i r

3、定长编码定理和定长编码方法 对信源U的N次扩展信源UJ进行r进制编 码 无失真条件: rw≥q 整理得 ≥ 0g9_ N logr H)=) logr 第四章离散无记忆信源 信息理论与编码 10 无失真编码
第四章 离散无记忆信源 无失真编码 信息理论与编码 10 3、定长编码定理和定长编码方法 对信源U的N次扩展信源 进行r进制编 码 无失真条件: 整理得 N U l N N r q max max log ( ) ( ) log log N r l H U q H U N r r