
第2章信道与噪声 2.1信道的定义与分类 2.2信道的组成与模型 2.3恒参信道及其对所传信号的影响 2.4变参信道及其对所传信号的影响 2.5信道带宽、系统带宽与信号带宽2.6随机过程的基本概念 2.7信道常见噪声及特征 28信道容量的概念(香农公式)
第2章 信道与噪声 2.1 信道的定义与分类 2.2 信道的组成与模型 2.3 恒参信道及其对所传信号的影响 2.4 变参信道及其对所传信号的影响 2.5 信道带宽、系统带宽与信号带宽 2.6 随机过程的基本概念 2.7 信道常见噪声及特征 2.8 信道容量的概念(香农公式)

2.1信道的定义与分类 1.信道的定义 信道是指定的一段频带,它既让信号通过, 同时又会给信号施以限制和损害。信道的根本 作用是传输信号。 2.信道的分类 图2.1信道的分类
2.1 信道的定义与分类 1. 信道的定义 信道是指定的一段频带,它既让信号通过, 同时又会给信号施以限制和损害。信道的根本 作用是传输信号。 2. 信道的分类 图2.1 信道的分类
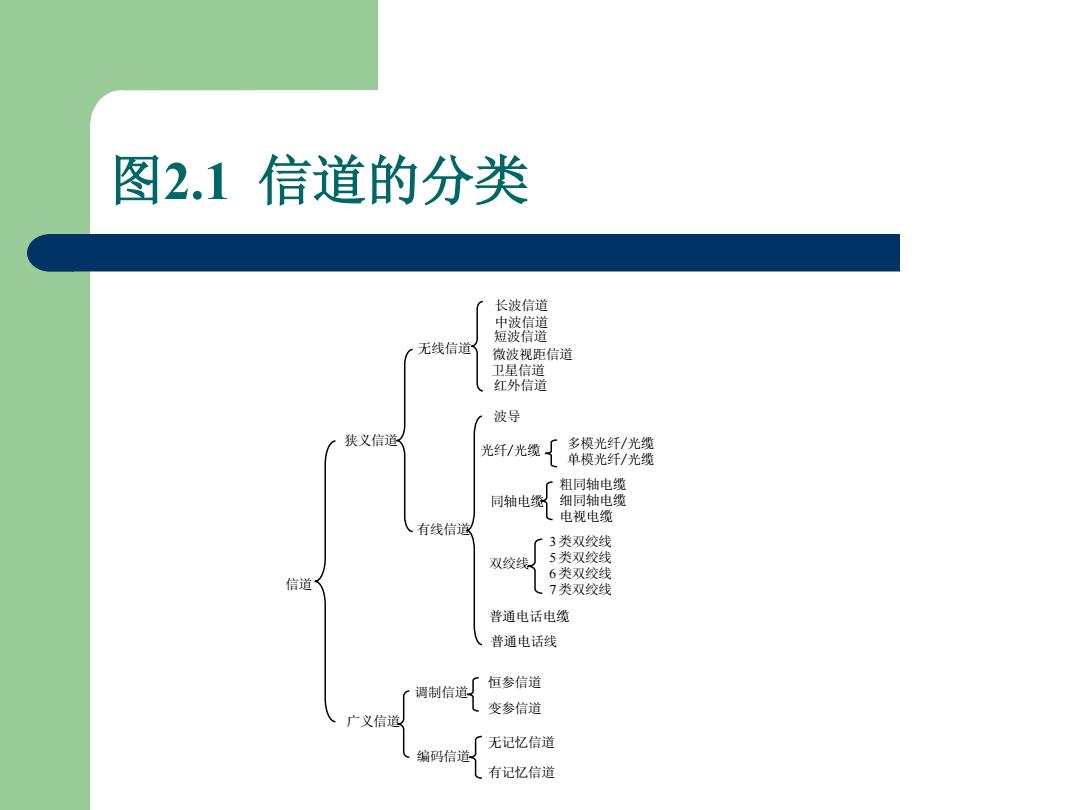
图2.1信道的分类 长波信道 中波信道 短波信道 无线信道 微波视距信道 卫星信道 红外信道 波导 狭义信道 光纤/光缆厂 多模光纤/光缆 单模光纤/光缆 粗同轴电缆 同轴电缆 细同轴电缆 电视电缆 有线信道 3类双绞线 双绞线 5类双绞线 6类双绞线 信道 7类双绞线 普通电话电缆 普通电话线 恒参信道 调制信道 变参信道 广义信道 无记忆信道 编码信道 有记忆信道
图2.1 信道的分类 信道 狭义信道 广义信道 调制信道 编码信道 恒参信道 变参信道 无记忆信道 有记忆信道 有线信道 无线信道 双绞线 同轴电缆 光纤/光缆 3类双绞线 5类双绞线 6类双绞线 7类双绞线 粗同轴电缆 细同轴电缆 电视电缆 多模光纤/光缆 单模光纤/光缆 长波信道 中波信道 短波信道 微波视距信道 卫星信道 波导 红外信道 普通电话线 普通电话电缆

2.2信道的组成与模型 2.2.1调制信道的组成 2.2.2编码信道的组成 2.2.3调制信道的数学模型 2.2.4编码信道的数学模型
2.2 信道的组成与模型 2.2.1 调制信道的组成 2.2.2 编码信道的组成 2.2.3 调制信道的数学模型 2.2.4 编码信道的数学模型

2.2.1调制信道的组成 调制信道是从研究调制和解调的基本问题 出发而提出的,它的范围是从调制器输出端到 解调器的所有转换器及传输媒介;不管其中间 过程如何,它们不过是把已调信号进行某种转 换而己,我们只需关心转换的最终结果,而无 需关心形成这个最终结果的详细过程。因此 研究调制与解调问题时,定义一个调制信道是 方便和恰当的。如图2.2所示
2.2.1 调制信道的组成 调制信道是从研究调制和解调的基本问题 出发而提出的,它的范围是从调制器输出端到 解调器的所有转换器及传输媒介;不管其中间 过程如何,它们不过是把已调信号进行某种转 换而已,我们只需关心转换的最终结果,而无 需关心形成这个最终结果的详细过程。因此, 研究调制与解调问题时,定义一个调制信道是 方便和恰当的。如图2.2所示
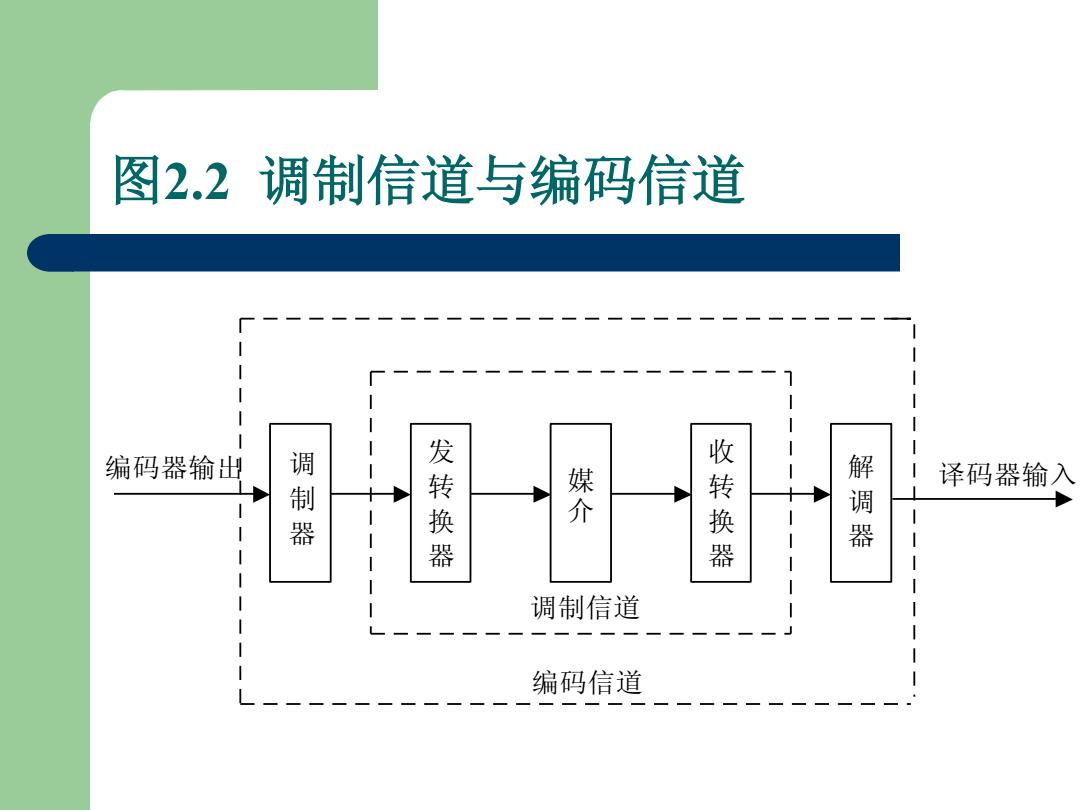
图2.2调制信道与编码信道 I 编码器输出 调 解 译码器输入 制 蝶 发转换 收转换 器 调制信道 编码信道
图2.2 调制信道与编码信道 调 制 器 发 转 换 器 媒 介 收 转 换 器 解 调 器 编码器输出 译码器输入 调制信道 编码信道

2.2.2编码信道的组成 在数字通信系统中,如果仅着眼于编码和 译码问题,则可定义到另一种广义信道一编 码信道。这是因为,从编码和译码的角度看 编码器的输出仍是某一数字序列,而译码器输 入同样也是一数字序列,它们在一般情况下是 相同的数字序列。因此,从编码器输出端到译 码器输入端的所有转换器及传输媒介可用一个 完成数字序列转换的方框加以概括,此方框称 为编码信道
2.2.2 编码信道的组成 在数字通信系统中,如果仅着眼于编码和 译码问题,则可定义到另一种广义信道——编 码信道。这是因为,从编码和译码的角度看, 编码器的输出仍是某一数字序列,而译码器输 入同样也是一数字序列,它们在一般情况下是 相同的数字序列。因此,从编码器输出端到译 码器输入端的所有转换器及传输媒介可用一个 完成数字序列转换的方框加以概括,此方框称 为编码信道

2.2.3调制信道的数学模型 (1) 有一对(或多对)输入端,则必然有一对(或多对)输 出端; (2 绝大部分信道是线性的,即满足叠加原理: (3) 信号通过信道需要一定的迟延时间; (4) 信道对信号有损耗(固定损耗或时变损耗); (5) 即使没有信号输入,在信道输出端仍可能有一定 的功率输出(噪声)。 可用一个二对端(或多对端)的时变线形网络去替代调 制信道。这个网络就称作调制信道模型,如图2.3所示
2.2.3 调制信道的数学模型 (1) 有一对(或多对)输入端,则必然有一对(或多对)输 出端; (2) 绝大部分信道是线性的,即满足叠加原理; (3) 信号通过信道需要一定的迟延时间; (4) 信道对信号有损耗(固定损耗或时变损耗); (5) 即使没有信号输入,在信道输出端仍可能有一定 的功率输出(噪声)。 可用一个二对端(或多对端)的时变线形网络去替代调 制信道。这个网络就称作调制信道模型,如图2.3所示
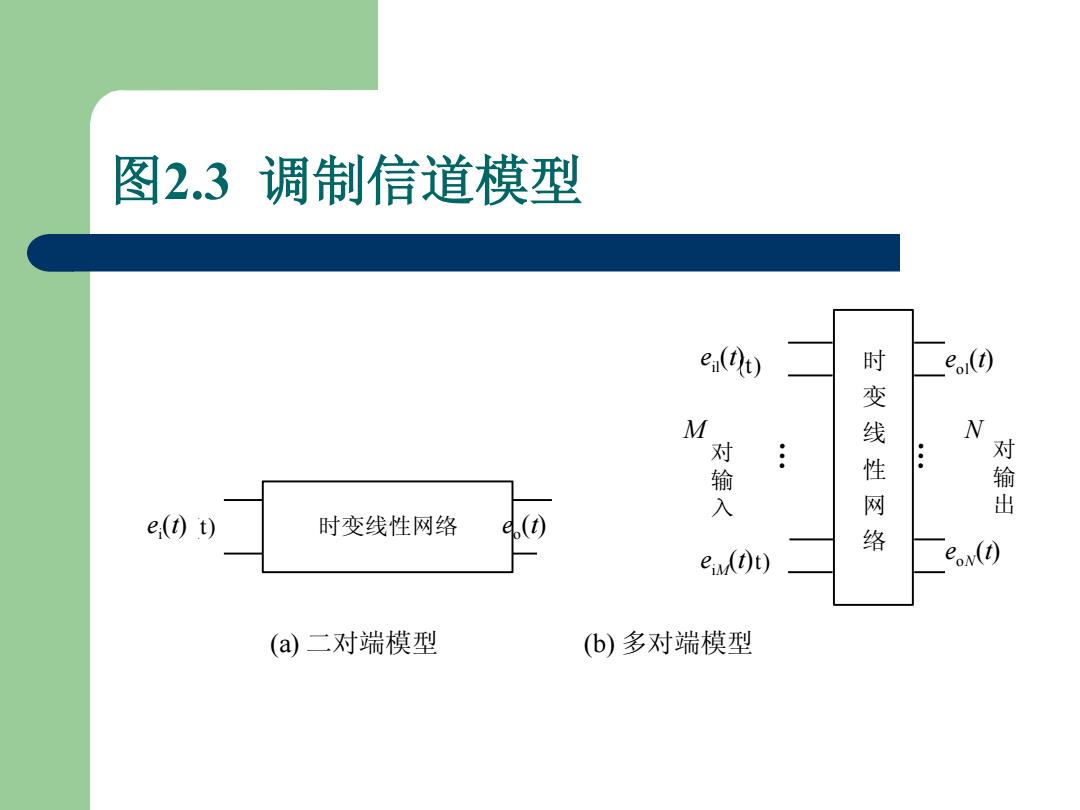
图2.3调制信道模型 e,Dt 时 e.() M 线 N 输 对 入 网 出 e,(0t) 时变线性网络 () 络 eiM(D)t) eoN(t) (a)二对端模型 (b)多对端模型
图2.3 调制信道模型 时变线性网络 时 变 线 性 网 络 M 对 输 入 N 对 输 出 e (t) e (t) e (t) e (t) e (t) e (t) i 0 i1 iM 0 1 0 N (a) (b) (a) 二对端模型 (b) 多对端模型 ei (t) eo (t) eil(t) M eiM (t) eo l(t) eoN (t) N … …

2.2.4编码信道的数学模型 编码信道是包括调制信道和调制器、解调器在内的 信道。 由于编码信道包含调制信道,因而它同样要受到调 制信道的影响。但是,从编/译码的角度看,以上这个 影响已被反映在解调器的最终结果里 一使解调器输 出数字序列以某种概率发生差错。显然,如果调制信 道特性越差,即特性越不理想、加性噪声越严重,则 发生错误的概率将会越大。由此看来,编码信道的模 型可用数字信号的转移概率来描述
2.2.4 编码信道的数学模型 编码信道是包括调制信道和调制器、解调器在内的 信道。 由于编码信道包含调制信道,因而它同样要受到调 制信道的影响。但是,从编/译码的角度看,以上这个 影响已被反映在解调器的最终结果里——使解调器输 出数字序列以某种概率发生差错。显然,如果调制信 道特性越差,即特性越不理想、加性噪声越严重,则 发生错误的概率将会越大。由此看来,编码信道的模 型可用数字信号的转移概率来描述