
红黑树 一种重要的平衡二叉搜索树实现方法 陶先平
红黑树 一种重要的平衡二叉搜索树实现方法 陶先平

平衡二叉搜索树 我们有没有简单的方法得到一棵相对“平衡的”二叉搜索树? 何谓“相对”平衡 简单到什么程度?
平衡二叉搜索树 我们有没有简单的方法得到一棵相对“平衡的”二叉搜索树? 何谓“相对”平衡 简单到什么程度?

红黑树的基本性质 ·Binary Search Tree Each node of the tree now contains the attributes color,key,left, right,and p. 1.Every node is either red or black. 2.The root is black. red-black trees ensure that no such path is more than twice as 3.Every leaf (NIL)is black. long as any other,so that the tree is approximately balanced 4.If a node is red,then both its children are black. 5. For each node,all simple paths from the node to descendant leaves contain the same number of black nodes
红黑树的基本性质 • Binary Search Tree • Each node of the tree now contains the attributes color, key, left, right, and p. red-black trees ensure that no such path is more than twice as long as any other, so that the tree is approximately balanced
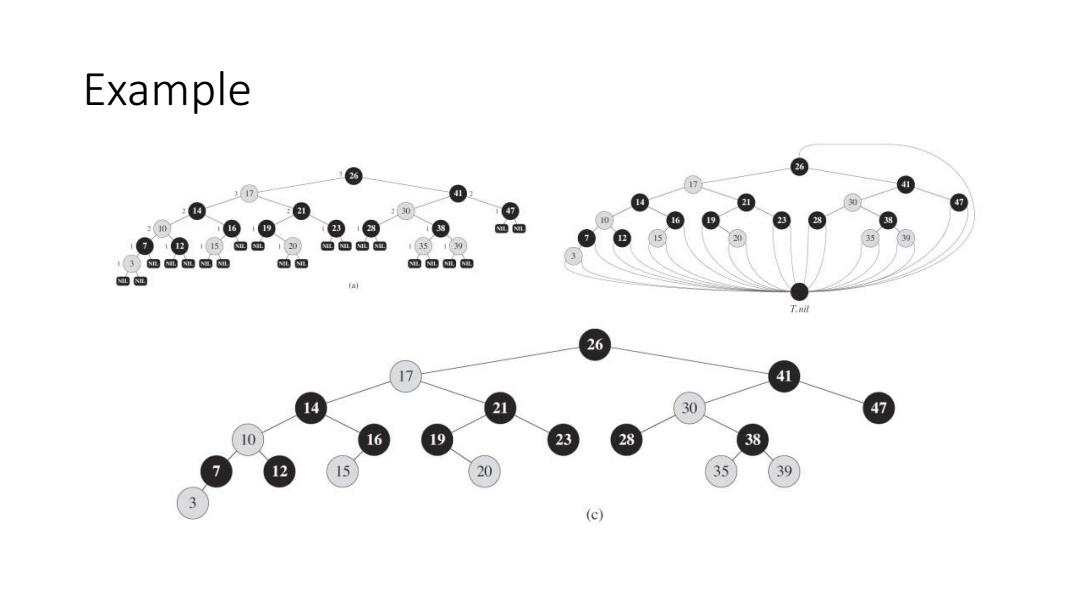
Example 7 130 0 60 m ⑦1D5如m10)如血m西 135130 13如m血 如 6 A6 四m T.nl 26 17 41 14 21 30 47 10 16 19 23 28 38 20 35 39 3 (c)
Example
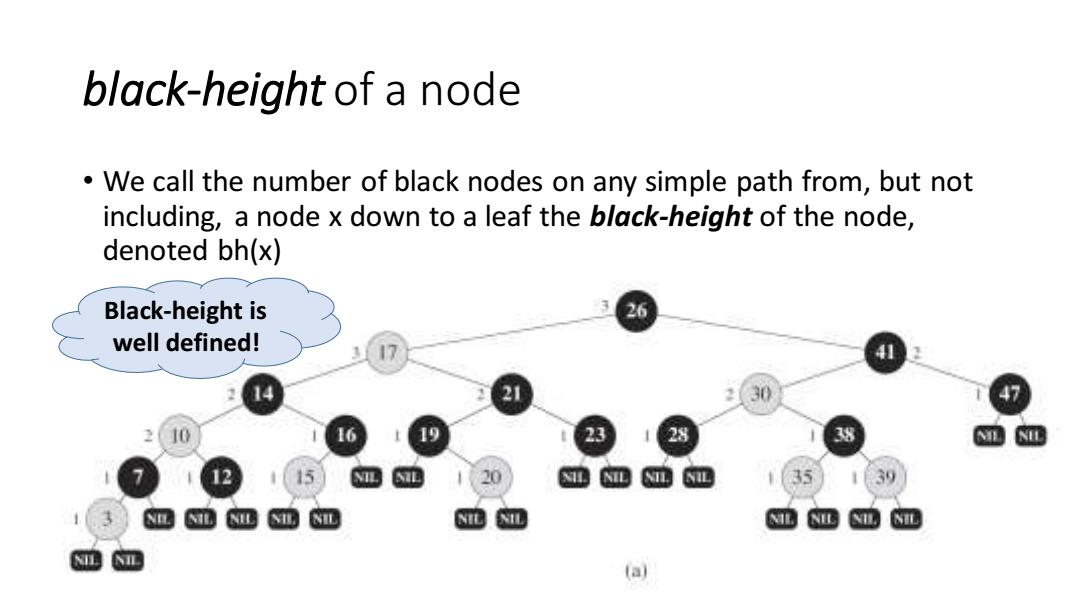
black-height of a node We call the number of black nodes on any simple path from,but not including,a node x down to a leaf the black-height of the node, denoted bh(x) Black-height is well defined! 39 NIL NIL D NIL a
black-height of a node • We call the number of black nodes on any simple path from, but not including, a node x down to a leaf the black-height of the node, denoted bh(x) Black-height is well defined!

Lemma 13.1 A red-black tree with n internal nodes has height at most 21g(n+1). ●Proof:. We start by showing that the subtree rooted at any node x contains at least 2bh(x)-1 internal nodes. If x is the root,the tree contains at least 2bh(root)-1 internal nodes ·n≥2 bh(root))-1 Let h be the height of the tree.The black-height of the root must be at least h/2;thus,n22h/2-1
• Proof: • We start by showing that the subtree rooted at any node x contains at least 2bh(x) -1 internal nodes. • If x is the root, the tree contains at least 2bh(root) -1 internal nodes • n≥ 2 bh(root) -1 • Let h be the height of the tree. The black-height of the root must be at least h/2; thus, n≥2 h/2 -1

Subtree rooted at any node x contains at least 2bh(x)-1 internal nodes Proof (induction on the height of x): ·Base: If the height of x is 0,then x must be a leaf(T.nil),and the subtree rooted at x indeed contains at least 20-1=0 internal nodes 。Induction: Suppose x has positive height and is an internal node with two children. Each child has a black-height of either bh(x)or bh(x)-1,depending on whether its color is red or black Since the height of a child of x is less than the height of x itself,we can apply the inductive hypothesis to conclude that each child has at least 2bh(x)-1-1 internal nodes. Thus,the subtree rooted at x contains at least(2bh(x)-1-1)+(2bh(x)-1-1)+1=2bh(x)-1 internal nodes
• Proof (induction on the height of x): • Base: • If the height of x is 0, then x must be a leaf (T.nil), and the subtree rooted at x indeed contains at least 20 -1 = 0 internal nodes • Induction: • Suppose x has positive height and is an internal node with two children. • Each child has a black-height of either bh(x) or bh(x)-1, depending on whether its color is red or black • Since the height of a child of x is less than the height of x itself, we can apply the inductive hypothesis to conclude that each child has at least 2bh(x)-1 -1 internal nodes. • Thus, the subtree rooted at x contains at least (2bh(x)-1 -1)+ (2bh(x)-1 -1)+1=2bh(x) -1 internal nodes Subtree rooted at any node x contains at least 2bh(x) -1 internal nodes
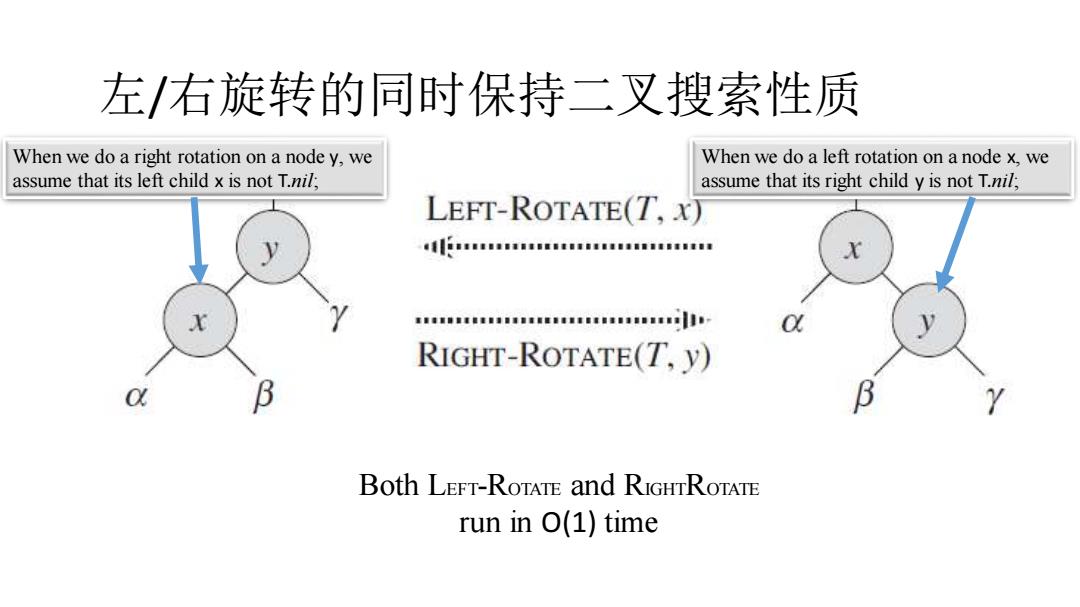
左/右旋转的同时保持二叉搜索性质 When we do a right rotation on a node y,we When we do a left rotation on a node x,we assume that its left child x is not T.nil; assume that its right child y is not T.nil; LEFT-ROTATE(T.x) RIGHT-ROTATE(T,y) Both Left-RoTATE and RightRoTATe run in O(1)time
左/右旋转的同时保持二叉搜索性质 When we do a left rotation on a node x, we assume that its right child y is not T.nil; Both LEFT-ROTATE and RIGHTROTATE run in O(1) time When we do a right rotation on a node y, we assume that its left child x is not T.nil;
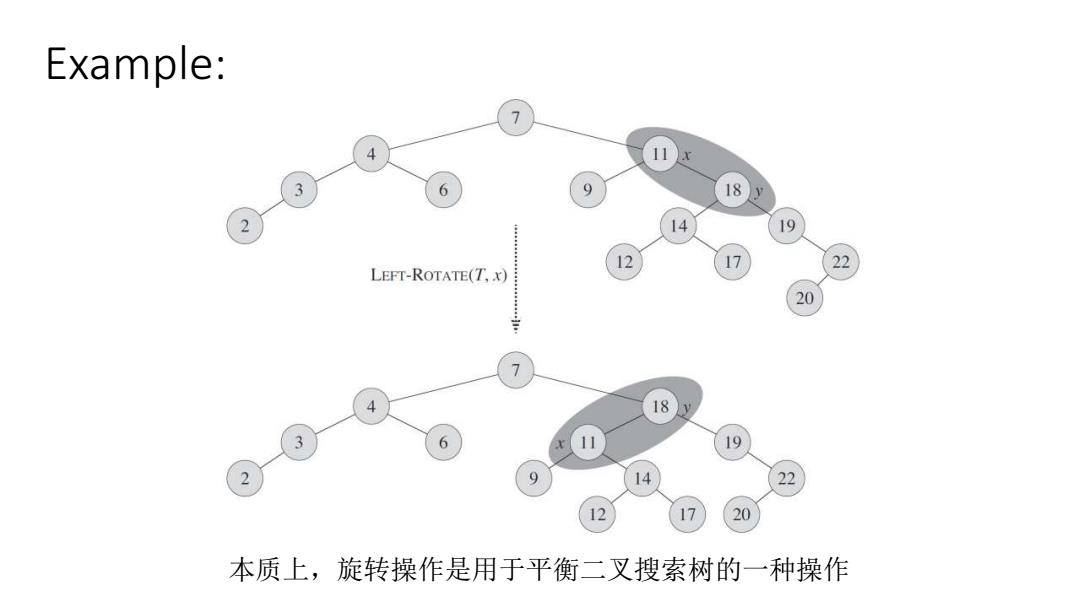
Example: 7 11 6 9 18y 14 19 12 22 LEFT-ROTATE(T,x) 20 18 6 19 9 4 本质上,旋转操作是用于平衡二叉搜索树的一种操作
Example: 本质上,旋转操作是用于平衡二叉搜索树的一种操作

红黑树的插入操作 ·采用BST的插入算法进行插入。插入元素的color被置为red。 ·这样的插入操作会破坏红黑树的特征吗? ·会! ·如果是插入的是根节点,破坏第二条 ·根是黑节点 ·如果插入的是叶节点,但是其父亲是red节点,破坏第四条 ·第四条:红色节点的子女必须是黑节点 其它几条会破 坏吗?
红黑树的插入操作 • 采用BST的插入算法进行插入。插入元素的color被置为red。 • 这样的插入操作会破坏红黑树的特征吗? • 会! • 如果是插入的是根节点,破坏第二条 • 根是黑节点 • 如果插入的是叶节点,但是其父亲是red节点,破坏第四条 • 第四条:红色节点的子女必须是黑节点 其它几条会破 坏吗?