
计算机问题求解一论题2-5 递归及其数学基础 2022年03月23日
计算机问题求解 – 论题2-5 - 递归及其数学基础 2022年03月23日

问题1: 以Hanoi Tower为例,说说你对“递归思想”、 “递归过程”、“递归式”的理解
以Hanoi Tower为例,说说你对“递归思想”、 “递归过程”、“递归式”的理解

最简单的解递归的方法一回朔 T(1)=1 T(n)=2T(n-1)+1 T()-2T(-1)+ 2T(m-1)=4T(n-2)大2 4Tm-2)=8Tm-3)+4人 Tn)=2"-1 2m-2T(2)(2m-1T(1)+2n-2
最简单的解递归的方法 – 回朔

问题2: 这里的解递归武和前一次讨论中的解 递归式有什么区别?
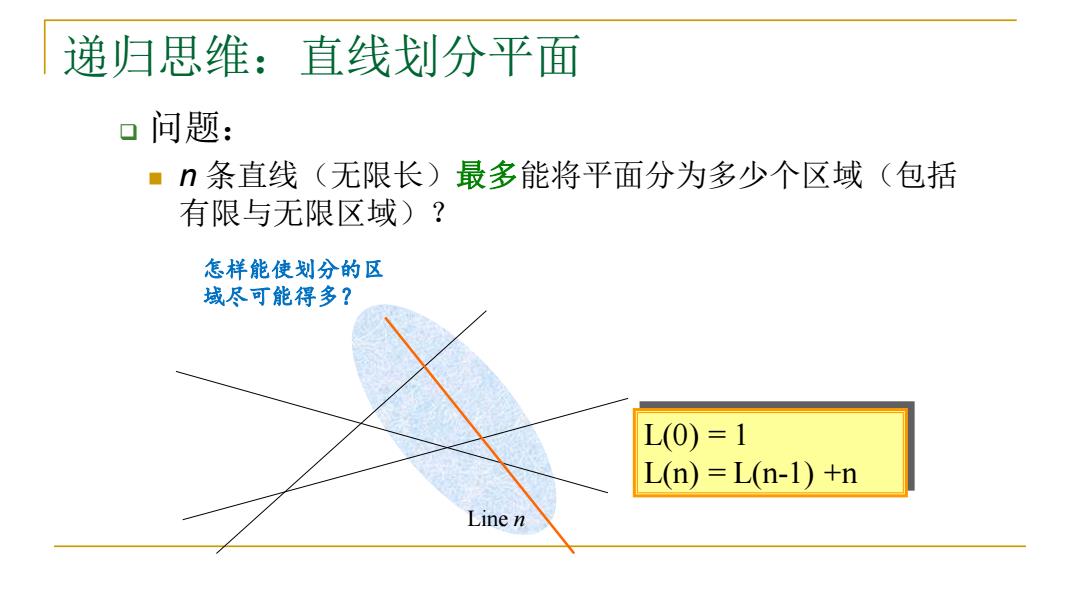
递归思维:直线划分平面 口问题: ·n条直线(无限长)最多能将平面分为多少个区域(包括 有限与无限区域)? 怎样能使划分的区 域尽可能得多? L(0)=1 L(n)=L(n-1)+n Line n
递归思维:直线划分平面 ❑ 问题: ◼ n 条直线(无限长)最多能将平面分为多少个区域(包括 有限与无限区域)? Line n 怎样能使划分的区 域尽可能得多? L(0) = 1 L(n) = L(n-1) +n

用回朔的办法解递归 L(m)=L(-1)+n =L(n-2)+(n-1)+n =L(n-3)+(m-2)+(n-1)+n =L(0)+1+2+..+(n-2)t(n-1)tn L(m=n(n+)/2+1
用回朔的办法解递归 L(n) = L(n-1)+n = L(n-2)+(n-1)+n = L(n-3)+(n-2)+(n-1)+n = …… = L(0)+1+2+……+(n-2)+(n-1)+n L(n) = n(n+1)/2 + 1

递归思维:Josephus问题 Live or die,it's a problem! Legend has it that Josephus wouldn't have lived to become famous without his mathematical talents.During the Jewish Roman war,he was among a band of 41 Jewish rebels trapped in a cave by the Romans.Preferring suicide to capture,the rebels decided to form a circle and,proceeding around it,to kill every third remaining person until no one was left.But Josephus,along with an unindicted co-conspirator,wanted none of this suicide nonsense;so he quickly calculated where he and his friend should stand in the vicious circle. We use a simpler version: “every second
递归思维:Josephus 问题 ◼ Live or die, it’s a problem! ◼ Legend has it that Josephus wouldn't have lived to become famous without his mathematical talents. During the Jewish Roman war, he was among a band of 41 Jewish rebels trapped in a cave by the Romans. Preferring suicide to capture, the rebels decided to form a circle and, proceeding around it, to kill every third remaining person until no one was left. But Josephus, along with an unindicted co-conspirator, wanted none of this suicide nonsense; so he quickly calculated where he and his friend should stand in the vicious circle. We use a simpler version: “every second
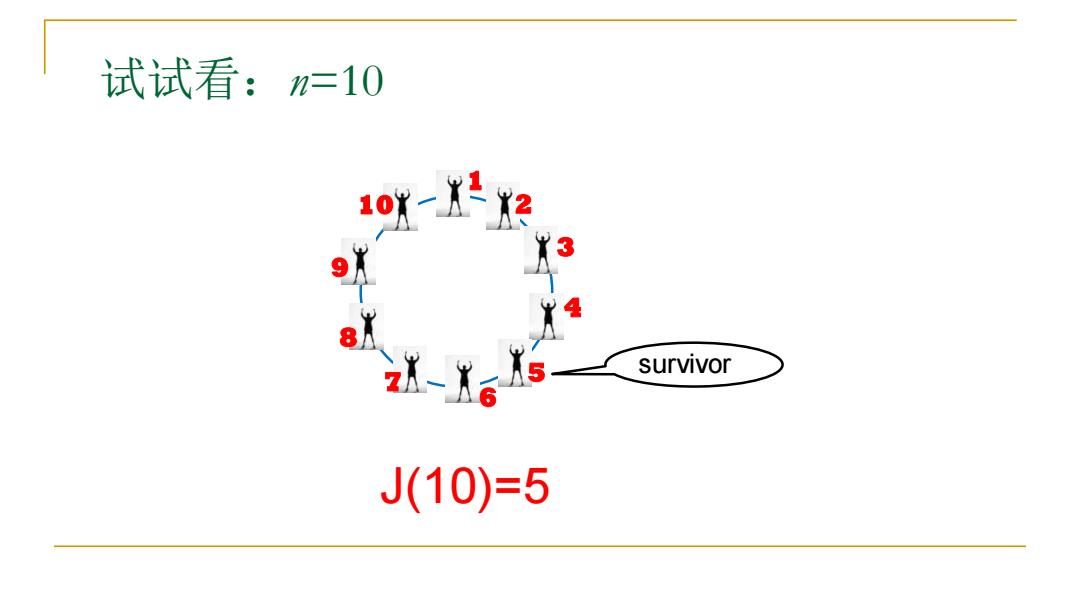
试试看:=10 101-2 ZK-K survivor J(10)=5
试试看:n=10 1 8 7 6 2 4 5 10 3 9 survivor J(10)=5
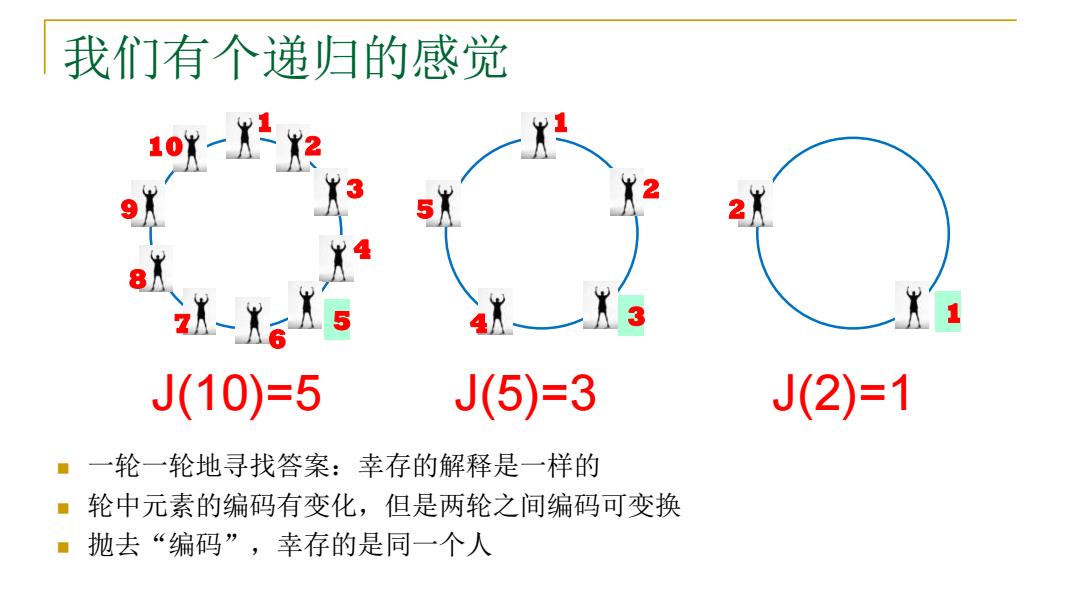
我们有个递归的感觉 10一 J(10)=5 J(5)=3 J(2)=1 ·一轮一轮地寻找答案:幸存的解释是一样的 ·轮中元素的编码有变化,但是两轮之间编码可变换 ”抛去“编码”,幸存的是同一个人
我们有个递归的感觉 ◼ 一轮一轮地寻找答案:幸存的解释是一样的 ◼ 轮中元素的编码有变化,但是两轮之间编码可变换 ◼ 抛去“编码”,幸存的是同一个人 1 8 7 6 2 4 5 10 3 9 J(10)=5 1 4 3 2 5 1 2 J(5)=3 J(2)=1
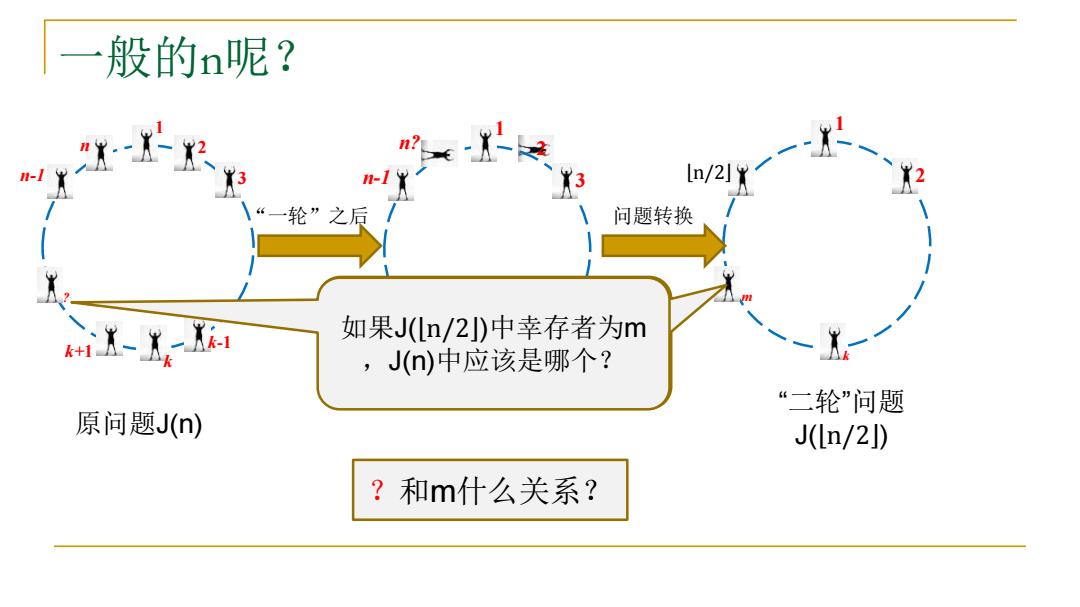
一般的n呢? 3 In/2]Y “一轮”之后 问题转换 如果J(n/2)中幸存者为m ,J()中应该是哪个? “二轮”问题 原问题J(n) J(In/2J) ?和m什么关系?
一般的n呢? 1 n 2 n-1 3 k+1 k k-1 “一轮”之后 原问题J(n) 1 n? 2 n-1 3 k k+1 k-1 1 ہn/2ۂ 2 k “二轮”问题 J(ہn/2ۂ( 问题转换 ? m 如果J(ہn/2ۂ(中幸存者为m ,J(n)中应该是哪个? 如果J(ہn/2ۂ(中幸存者为m ,J(n)中应该是哪个? ?和m什么关系?