
计算机问题求解一论题3-1 动态规划 2022年09月07日
计算机问题求解 – 论题3-1 - 动态规划 2022年09月07日
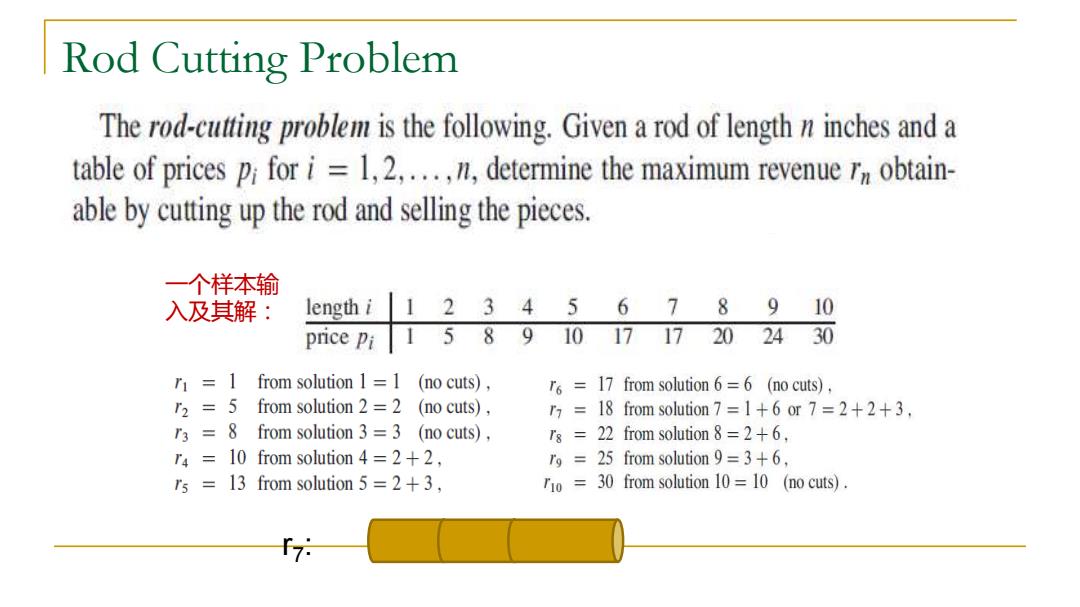
Rod Cutting Problem The rod-cuing problem is the following.Given a rod of length n inches and a table of prices pifor i=1,2,....n,determine the maximum revenue r obtain- able by cutting up the rod and selling the pieces. 一个样本输 入及其解: length i 11234 567 9 8 10 price Pi 1 589 10171720 2430 r=1 from solution 1=1 (no cuts), r =17 from solution 6=6 (no cuts), r2=5 from solution 2=2 (no cuts), 7=18 from solution 7 =1+6 or 7=2+2+3, r3 =8 from solution 3=3 (no cuts), rs 22 from solution 8=2+6. r4 10 from solution 4=2+2, r9 25 from solution 9=3+6, rs 13 from solution 5=2+3, rio 30 from solution 10=10 (no cuts). f7:
Rod Cutting Problem 一个样本输 入及其解: r7 :

问题1: 这个问题的解空间有多 大?为什么?

问题2 如何搜索?可以压缩解空间吗? 似乎任何一个可行解, 都可能是最优解 和我们之前看到的“猜年龄”、“求直径”似乎都不一样
似乎任何一个可行解, 都可能是最优解 和我们之前看到的“猜年龄”、“求直径”似乎都不一样

有没有必要遍历解空间?我 们似乎有另外一个“空间”: 问题空间!
有没有必要遍历解空间?我 们似乎有另外一个“空间”: 问题空间!

问题3:如何思考? 总存在最优方案,最优方案总有第一刀! 第一刀切下去之后: 针对任意的r,我们能够写出下面的公式! Tn=ri+rn-i 这个公式well define吗? 最优子结构性质! r+rn一定是rn吗? 我们姑且放一放
rn : i rn =ri+rn-i 总存在最优方案,最优方案总有第一刀! 第一刀切下去之后: 针对任意的rn,我们能够写出下面的公式! 这个公式well define吗? ri+rn-i一定是rn吗? 最优子结构性质! 我们姑且放一放

间题4:我们知道应该是多少吗? In: Tn=ri+rn-i 从0开始遍历! In max (Pn,1 Fn-1,2+In-2;...,In-1+1)
rn : i rn =ri+rn-i 从0开始遍历!

更关键的是:我们从公式中的求解中, 看到了什么? In [n=ri+rn-i 递归!
rn : i rn =ri+rn-i 递归!

递归的解法:扫描所有可能的割法 In max (Pn,rI In-1,r2 +In-2,...,In-1+r1) max (Pi+rn-i) <i<刀 Cut-Rod(p,n){ P:价格表,n:长度 if n==0 return 0; q=-1; for(i=1 to n){ ∥递归遍历所有的“割法” q max(q,p[i]+Cut-Rod(p,n-i)) } return q;
递归的解法:扫描所有可能的割法 Cut-Rod(p,n) { //P:价格表,n:长度 if n==0 return 0; q=-1; for( i=1 to n) { //递归遍历所有的“割法” q = max(q, p[i]+Cut-Rod(p, n-i)) } return q; }

递归的解法: CUT-ROD(P,n) 当n=4时,递归调用树: 1 fn==0 2 return O 3q=-00 4 for i Iton q max(g.pli]+CUT-ROD(p,n-i)) 6 return q 问题5: 为什么这个算法注定是低效率的?
递归的解法: 当n=4时,递归调用树: