
计算机问题求解一论题3-10 图的连通度 2022年11月16日
计算机问题求解 – 论题3-10 - 图的连通度 2022年11月16日
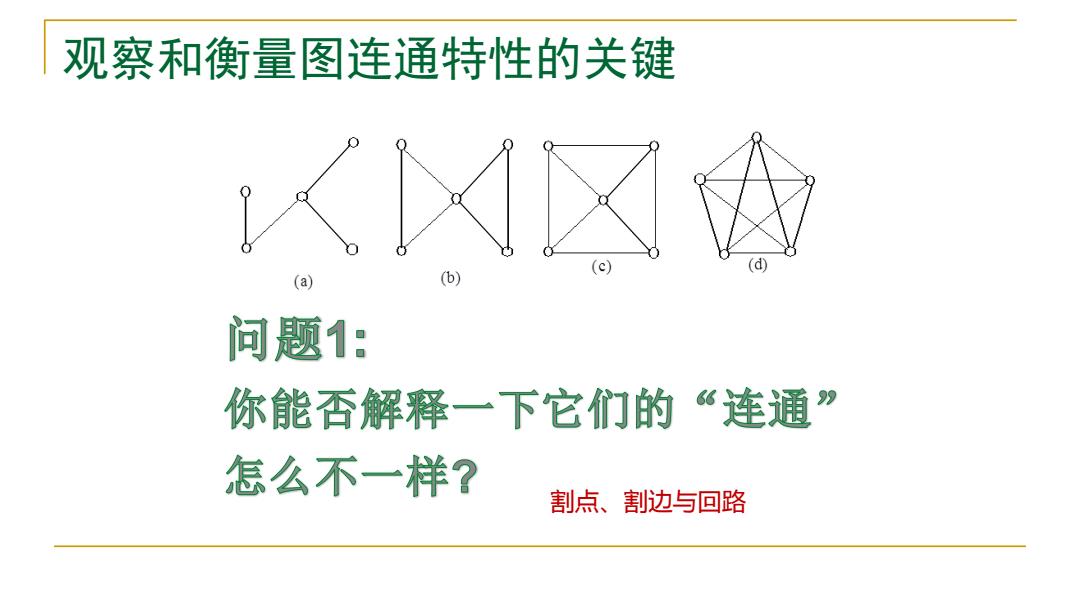
观察和衡衡量图连通特性的关键 问题1: 你能否解释一下它们的“连通” 怎么不一样? 割点、割边与回路
观察和衡量图连通特性的关键 割点、割边与回路

围绕割点的若干结论 Theorem 5.1 Let v be a vertex incident with a bridge in a connected graph G.Then v is a cut- vertex of G if and only if degv=2. Corollary 5.2 Let G be a connected graph of order 3 or more.If G contains a bridge,then G contains a cut-vertex. Theorem 5.3 Let v be a cut-vertex in a connected graph G and let u and w be vertices in distinct components of G-v.Then y lies on every u-w path in G. Corollary 5.4 A vertex v of a connected graph G is a cut-vertex of G if and only if there exist vertices u and w distinct from v such that v lies on every u-w path of G. Theorem 5.5 Let G be a nontrivial connected graph and let ueV(G).Ifv is a vertex that is farthest from u in G,then v is not a cut-vertex of G
围绕割点的若干结论

问题2 衡量连通的牢度”的指 标是什么?

指标1:minimum vertex-cut By a vertex-cut in a graph G,we mean a (strict) subset U of vertices of G such that G-U is disconnected. A vertex-cut of minimum cardinality in G is called a minimum vertex-cut
指标1:minimum vertex-cut By a vertex-cut in a graph 𝐺 , we mean a (strict) subset 𝑈 of vertices of 𝐺 such that 𝐺 − 𝑈 is disconnected. 𝐴 vertex-cut of minimum cardinality in 𝐺 is called a minimum vertex-cut
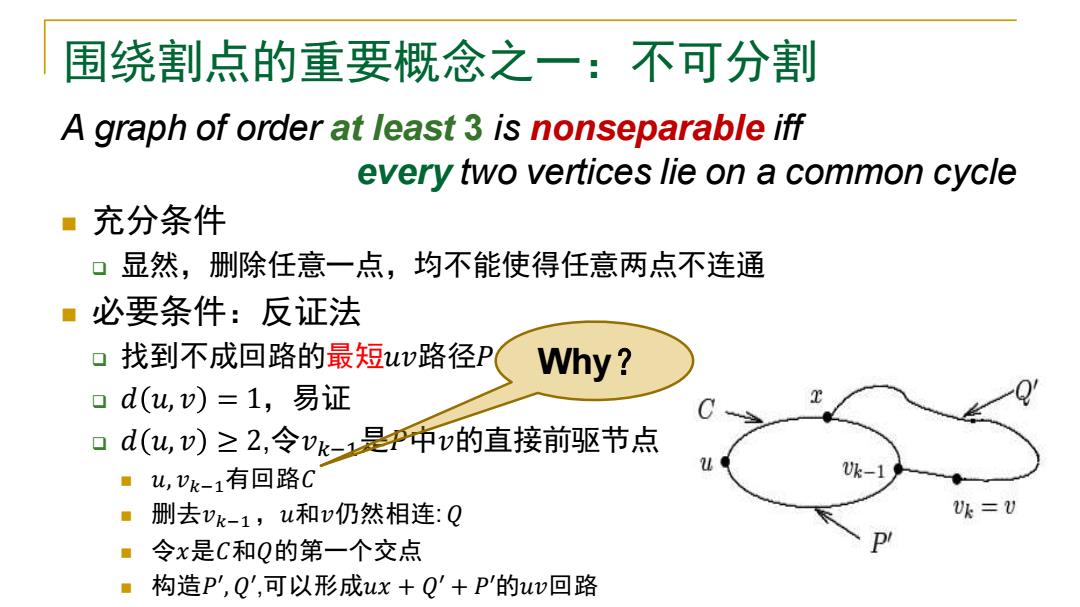
围绕割点的重要概念之一:不可分割 A graph of order at least 3 is nonseparable iff every two vertices lie on a common cycle ■充分条件 口显然,删除任意一点,均不能使得任意两点不连通 。必要条件:反证法 口找到不成回路的最短uw路径P Why? 口d(u,v)=1,易证 口d(u,v)≥2,令k-是P中v的直接前驱节点 ■u,vk-1有回路C ■删去vk-1,u和v仍然相连:Q Uk=U 令x是C和Q的第一个交点 构造P',Q,可以形成ux+Q'+P'的uw回路
围绕割点的重要概念之一:不可分割 A graph of order at least 3 is nonseparable iff every two vertices lie on a common cycle ◼ 充分条件 ❑ 显然,删除任意一点,均不能使得任意两点不连通 ◼ 必要条件:反证法 ❑ 找到不成回路的最短𝑢𝑣路径𝑃 ❑ 𝑑 𝑢, 𝑣 = 1,易证 ❑ 𝑑 𝑢, 𝑣 ≥ 2,令𝑣𝑘−1是𝑃中𝑣的直接前驱节点 ◼ 𝑢, 𝑣𝑘−1有回路𝐶 ◼ 删去𝑣𝑘−1,𝑢和𝑣仍然相连: 𝑄 ◼ 令𝑥是𝐶和𝑄的第一个交点 ◼ 构造𝑃′ , 𝑄′ ,可以形成𝑢𝑥 + 𝑄′ + 𝑃′的𝑢𝑣回路 Why?

围绕割点的重要概念之二:Bock A maximal nonseparable subgraph of a graph Gis called a block of G. 问题3:极大还 是最大?
围绕割点的重要概念之二:Block A maximal nonseparable subgraph of a graph G is called a block of G. 问题3:极大还 是最大?
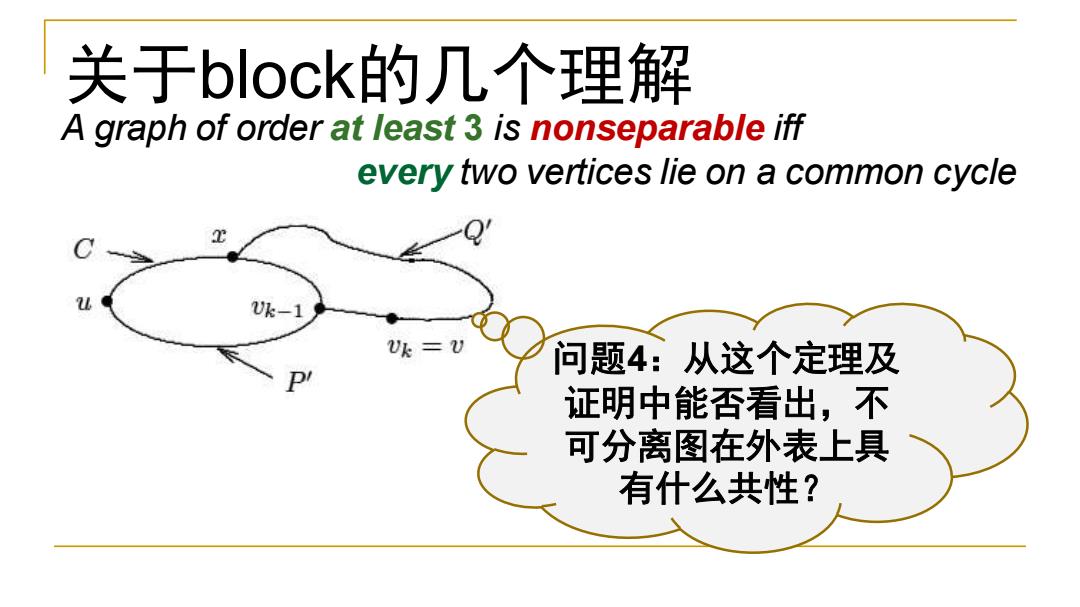
关于block的几个理解 A graph of order at least 3 is nonseparable iff every two vertices lie on a common cycle Uk-1 Uk=U 问题4:从这个定理及 证明中能否看出,不 可分离图在外表上具 有什么共性?
问题4:从这个定理及 证明中能否看出,不 可分离图在外表上具 有什么共性? 关于block的几个理解 A graph of order at least 3 is nonseparable iff every two vertices lie on a common cycle

关于block的几个理解 Theorem 5.8 Let R be the relation defined on the edge set of a nontrivial connected graph G by e Rf,where e,f EE(G),if e f or e and f lie on a common cycle of G.Then R is an equivalence relation. 用等价关系来描述边之间的关系,到底有何用意? 问题5:Block的“极大”特性和“等价类”有何关系? Each subgraph of G induced by the edges in an equivalence class is in fact a block of G
关于block的几个理解 Theorem 5.8 Let 𝑅 be the relation defined on the edge set of a nontrivial connected graph G by 𝒆 𝑹 𝒇, where 𝑒, 𝑓 ∈ 𝐸(𝐺), if 𝑒 = 𝑓 or 𝑒 and 𝑓 lie on a common cycle of 𝐺. Then 𝑅 is an equivalence relation. 用等价关系来描述边之间的关系,到底有何用意? Each subgraph of G induced by the edges in an equivalence class is in fact a block of G. 问题5:Block的“极大”特性和“等价类”有何关系?
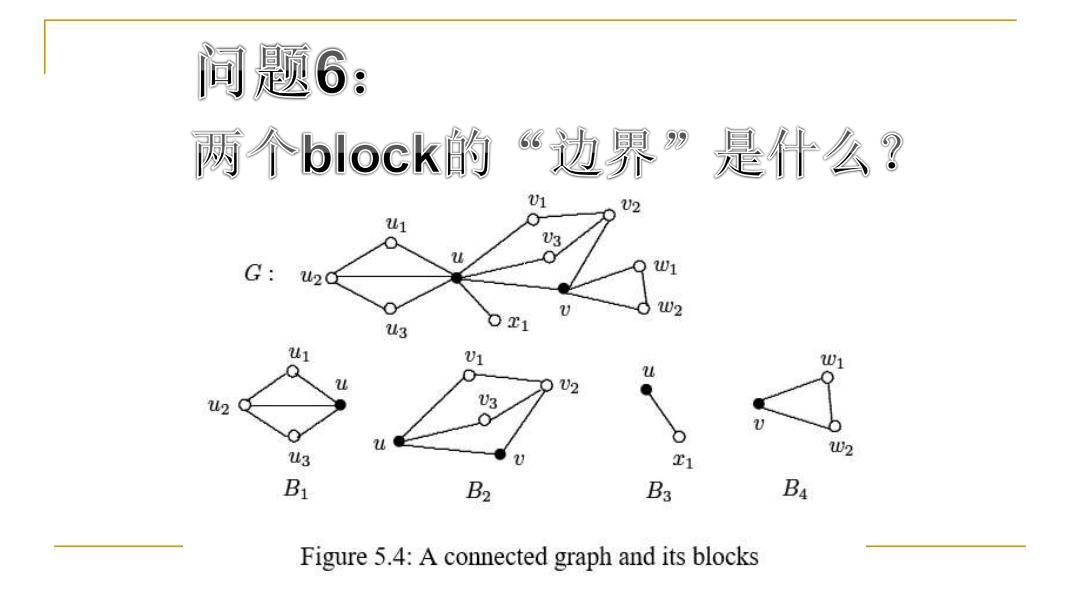
间题6: 两个bock的“边界”是什么? 1 U2 3 G:2 201 02 u3 01 V1 u W2 3 Bi B2 B3 Ba Figure 5.4:A connected graph and its blocks