
计算机问题求解-论题1-12 -偏序关系和格 2017年12-21
计算机问题求解--论题1-12 --偏序关系和格 2017年12-21

偏序关系 Suppose R is a relation on a set S satisfying the following three properties: [O](Reflexive)For any a e S,we have aRa. [O2](Antisymmetric)If a Rb and bRa,then a =b. [O3](Transitive)If a Rb and bRc,then aRc. Then R is called a partial order or,simply an order relation,and R is said to define a partial ordering of S.The s set S with the partial order is called a partially ordered set or,simply,an ordered set or poset.We write (S,R) when we want to specify the relation R
偏序关系

偏序关系 b器hy person wh business tion or trad be attended 问题1:查词典时,单词的“序”起 到了什么作用?单词的“序”是怎 么定义的? ·字母表中字母的序关系 ·积序关系(定义在偏序集之上) (a,b)(a',b')if a<a'andb<b' ·词典序关系(定义在全序集合之上) (a,b)<(a',b')if a<b or if a=a'andb<b' (a1,a2,....an)<(a,a2,....an)if ai=af for i 1,2,....k-1 and ak <ak
偏序关系 •问题1:查词典时,单词的“序”起 到了什么作用?单词的“序”是怎 么定义的? • 字母表中字母的序关系 • 积序关系(定义在偏序集之上) • 词典序关系(定义在全序集合之上)

偏序关系 bushy person wh business tion or trad be attended (a)Alphabetical (Lexicographical)Order:The reader is no doubt familiar with the usual alphabetical ordering of A*.That is: (i)<w,where A is the empty word and w is any nonempty word. (ii)Suppose u au'and v bu'are distinct nonempty words where a,b A and u',v'A*.Then u<v if a<b or if a=bbutu'<v' (b)Short-lex Order:Here A+is ordered first by length,and then alphabetically.That is,for any distinct words u,v in A*, u<v if lu<v or if lu=v but u precedes v alphabetically
偏序关系

偏序关系 bushy person wh business tion or trad be attended ·问题2: ·任意单词的长度有限 ·给定一个序关系,任意两个单词都可 以比较“序”,是否意味着单词的 “序位置”是唯一的?
偏序关系 •问题2: • 任意单词的长度有限 • 给定一个序关系,任意两个单词都可 以比较“序”,是否意味着单词的 “序位置”是唯一的?

全序:一种特殊的偏序关系 ·如果对,b∈A,a≤b和b≤a中有一个成立,则a,b可比。 ·设R是A上的偏序关系,如果A中的任意两个元素都是可 比的,则称R是A上的全序关系(或线序关系) ·举例(全序) 。实数集上的“不大于”关系≤、基于拉丁字母表的字典顺序
全序:一种特殊的偏序关系 • 如果对a, bA,a≼b和b≼a中有一个成立,则a,b可比。 • 设R是A上的偏序关系,如果A中的任意两个元素都是可 比的,则称R是A上的全序关系(或线序关系) • 举例(全序) • 实数集上的“不大于” 关系、基于拉丁字母表的字典顺序

偏序集上的“小于”关系及覆盖 ·设是偏序集 ·A上的“小于”关系<定义如下: x<y iff x≤yAx≠y ·元素y覆盖x定义如下: ·x<y,且不存在zEA使得x<z<y ·表示为:x《y ·“y是x的覆盖” “y是x的直接后继(immediate successor)
偏序集上的“小于”关系及覆盖 • 设 是偏序集 • A上的“小于”关系≺定义如下: 𝒙 ≺ 𝒚 iff 𝒙 ≼ 𝒚 ∧ 𝒙𝒚 • 元素y覆盖x定义如下: • x≺y,且不存在zA使得x≺z≺y • 表示为:𝒙 ≪ 𝒚 • “y是x的覆盖” • “y是x的直接后继(immediate successor)
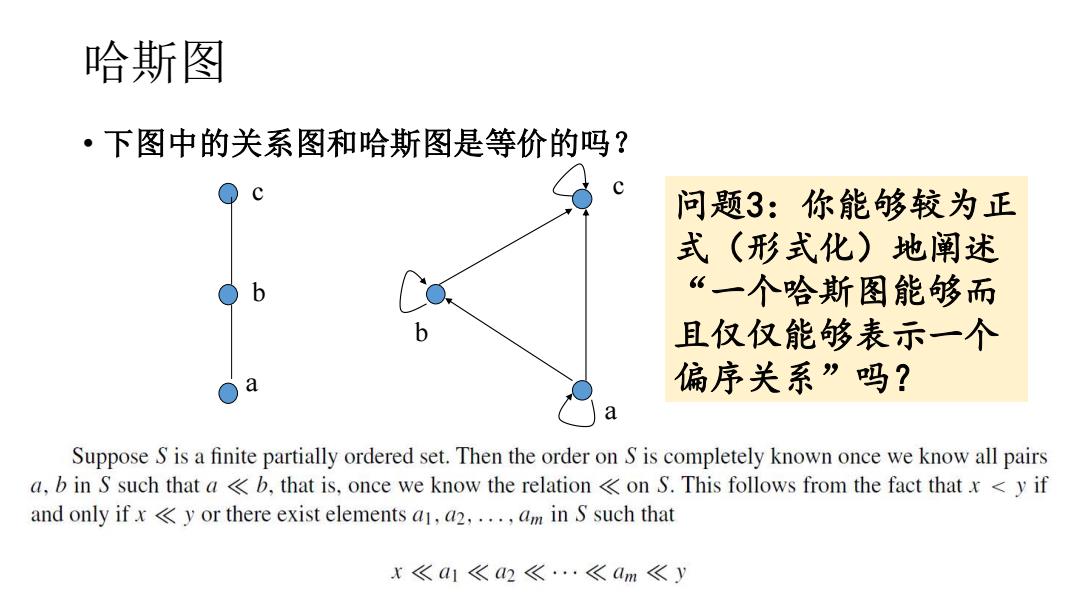
哈斯图 ·下图中的关系图和哈斯图是等价的吗? 问题3:你能够较为正 式(形式化)地阐述 “一个哈斯图能够而 且仅仅能够表示一个 a 偏序关系”吗? Suppose S is a finite partially ordered set.Then the order on S is completely known once we know all pairs a,b in S such that a <b,that is,once we know the relation on S.This follows from the fact thatx <y if and only ifx<y or there exist elements a1,a2,...,am in S such that x《a1《a2《·《am《y
哈斯图 • 下图中的关系图和哈斯图是等价的吗? a b c a b c 问题3:你能够较为正 式(形式化)地阐述 “一个哈斯图能够而 且仅仅能够表示一个 偏序关系”吗?
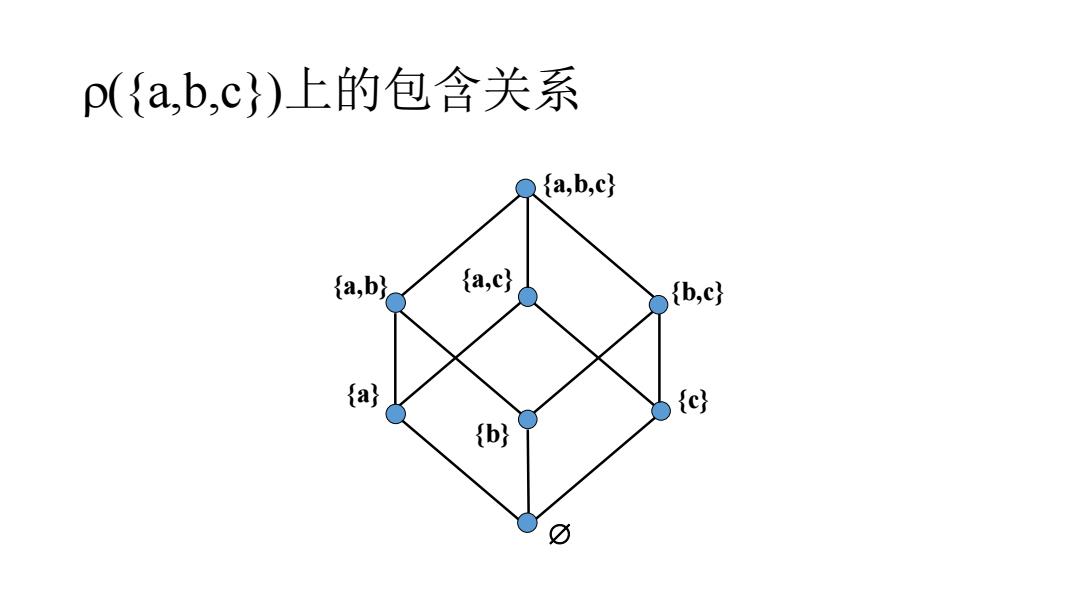
p({a,b,c)上的包含关系 fa,b,c} (a,b) {a,c} b,c} (a) c {b} 0
{a,b,c} {c} {b} {a} {b,c} {a,c} {a,b} ({a,b,c})上的包含关系
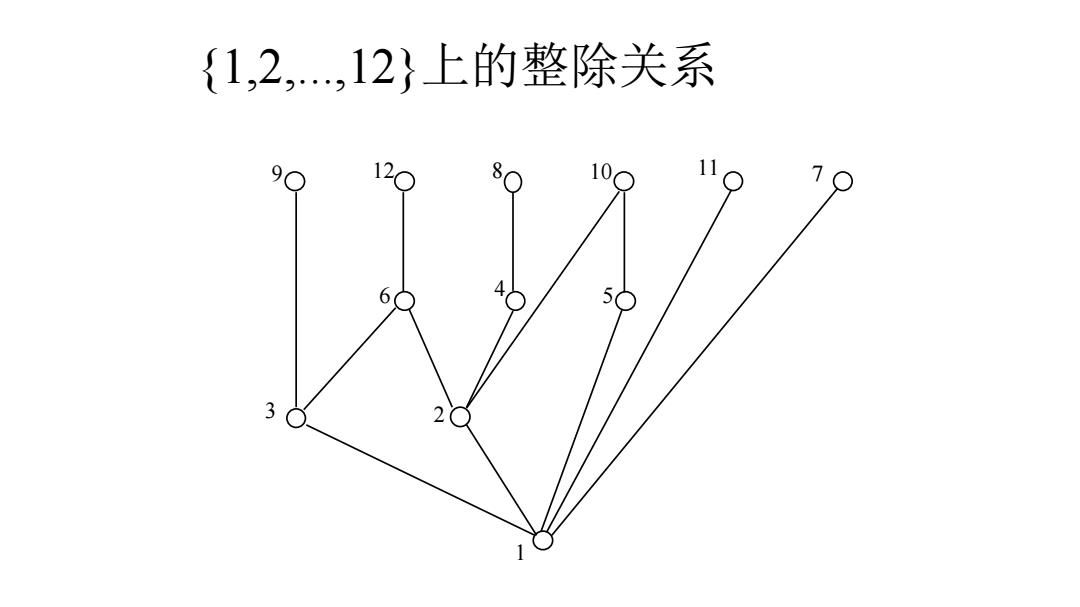
{1,2,12}上的整除关系 9 12O 80 10O 11 60 a 50 3 1
9 12 8 10 11 6 5 4 3 2 1 7 {1,2,...,12}上的整除关系