
上节回顾 2.3节大注入效应 小注入“结定律” 在N型区与耗尽区的边界处: pn(xn)=pno exp 在P型区与耗尽区的边界处: np(-xp)=npo exp kT 理想PN结的直流电流电压方程: exp
1 上节回顾 2.3节 大注入效应 小注入“结定律” 在 N 型区与耗尽区的边界处: p p p 0 ( ) exp qV n x n kT n n n0 ( ) exp qV p x p kT 在 P 型区与耗尽区的边界处: 理想PN 结的直流电流电压方程:
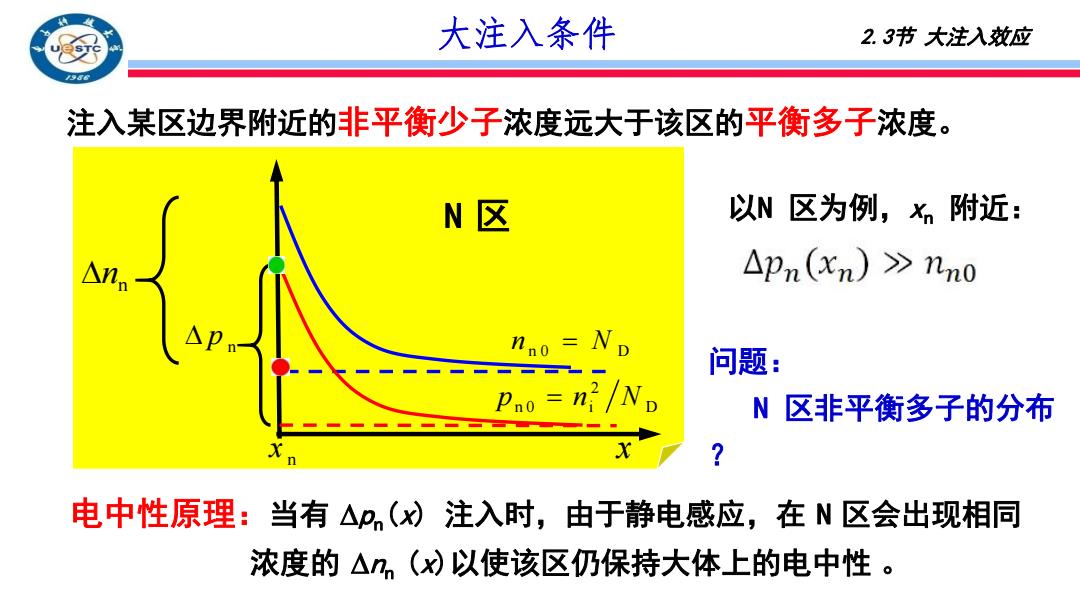
大注入条件 2.3节大注入效应 注入某区边界附近的非平衡少子浓度远大于该区的平衡多子浓度。 N区 以N区为例,X附近: n △pn(xn)>nn0 nno ND 问题: 区非平衡多子的分布 电中性原理:当有△,(W注入时,由于静电感应,在N区会出现相同 浓度的△n,(x以使该区仍保持大体上的电中性
2 大注入条件 2.3节 大注入效应 以N 区为例,xn 附近: n p n 0 D n N 2 n 0 i D p n N N 区 n x x n n 电中性原理:当有 pn(x) 注入时,由于静电感应,在 N 区会出现相同 浓度的 nn (x)以使该区仍保持大体上的电中性 。 注入某区边界附近的非平衡少子浓度远大于该区的平衡多子浓度。 问题: N 区非平衡多子的分布 ?
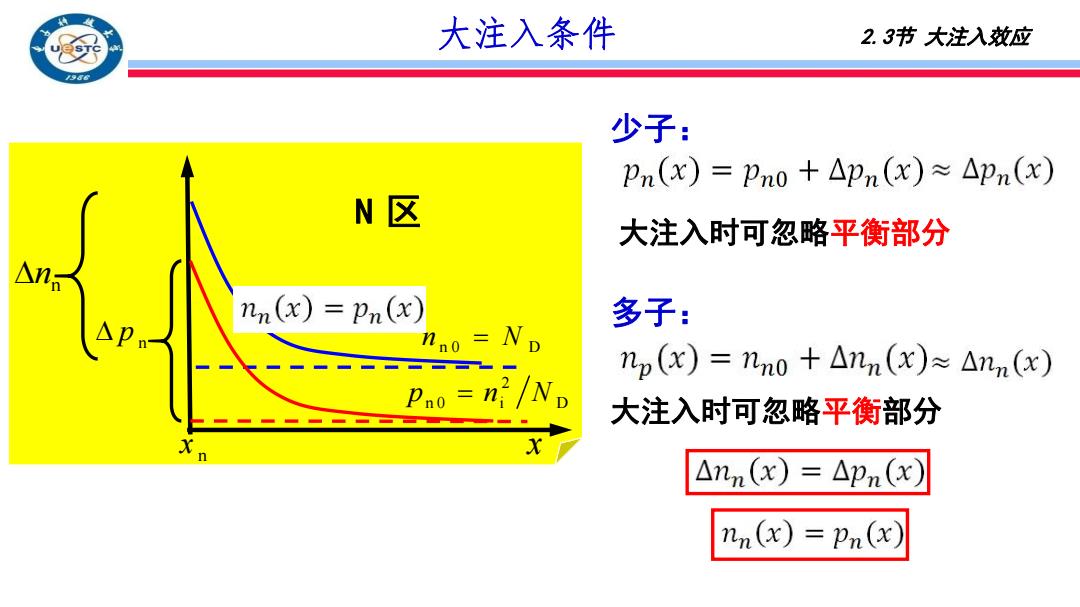
大注入条件 2.3节大注入效应 少子: pn(x)=pn0+△pn(x)≈△pn(x) N区 大注入时可忽略平衡部分 △n nn(x)=pn(x) 多子: nno =ND np(x)=nn0+△nn(x)≈△nn(x) 大注入时可忽略平衡部分 △nn(x)=△pn(x) nn(x)pn(x)
少子: 大注入时可忽略平衡部分 大注入时可忽略平衡部分 多子: 大注入条件 2.3节 大注入效应 n p n 0 D n N 2 n 0 i D p n N N 区 n x x n n
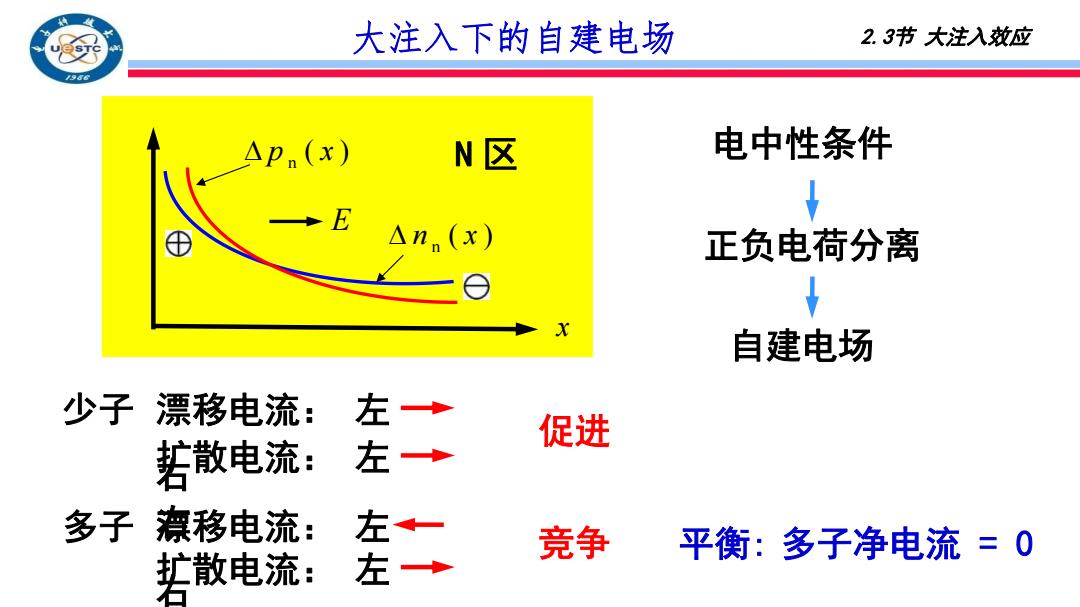
大注入下的自建电场 2.3节大注入效应 Ap(x) N区 电中性条件 △nn(x) 正负电荷分离 自建电场 少子漂移电流: 左 若散电流: 左 促进 多子潦移电流: 若散电流: 左左 竞争 平衡:多子净电流=0
p n ( x ) N 区 n n ( x ) E x 自建电场 大注入下的自建电场 正负电荷分离 漂移电流: 左 右 竞争 平衡: 多子净电流 = 0 扩散电流: 左 右 多子 少子 漂移电流: 左 右 促进 扩散电流: 左 右 2.3节 大注入效应 电中性条件

Webster:效应 2.3节大注入效应 dnn(x) 由多子净电流为零:Jn=qDn dx +qunnn(x)E=0. 得 Dn 1 dnn(x) E=- nn(x)pn(x) un nn(x) dx Dp 1 dpn(x) Dp up Pn(x) dx n p 代入空穴电流密度方程,得: Jp =-qDp dpn( dx 2+q4pPn(x)E=-q2Dp) dpn(x) dx 相当于空穴电流仍只由扩散电流构成,但扩散系数扩大了一倍。 这个现象称为Webster效应
得 由多子净电流为零: 2.3节 大注入效应 相当于空穴电流 仍只由扩散电流构成,但扩散系数扩大了一倍。 这个现象称为 Webster 效应。 代入空穴电流密度方程,得: Webster效应
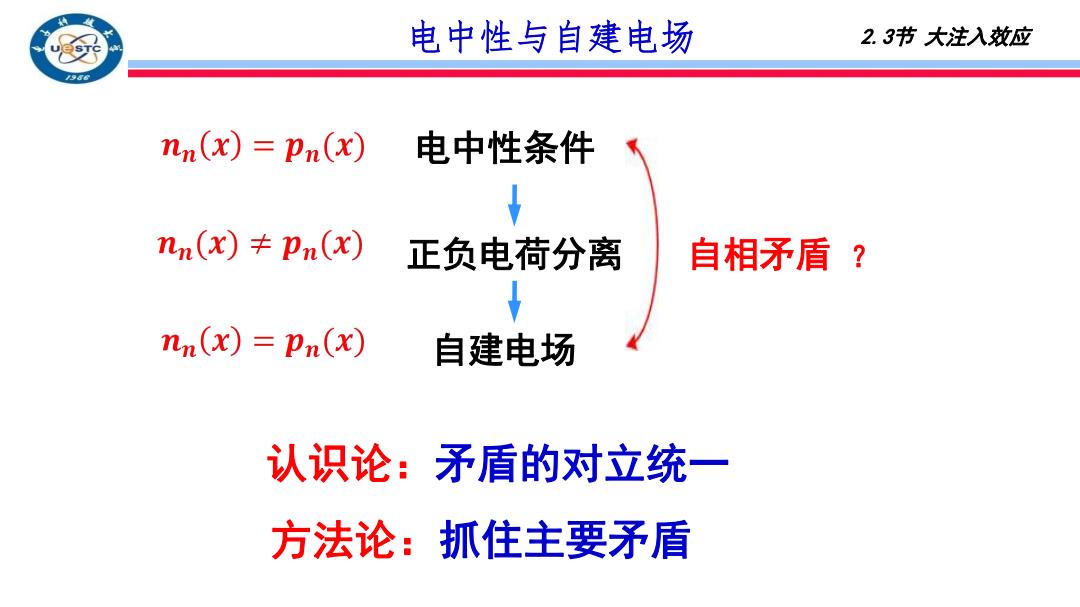
电中性与自建电场 2.3节大注入效应 nn(x)=pn(x) 电中性条件 nn(x)≠pn(x) 正负电荷分离 自相矛盾? nn(x)=Pn(x) 自建电场 认识论:矛盾的对立统一 方法论:抓住主要矛盾
2.3节 大注入效应 自相矛盾 ? 自建电场 正负电荷分离 电中性条件 认识论:矛盾的对立统一 方法论:抓住主要矛盾 电中性与自建电场
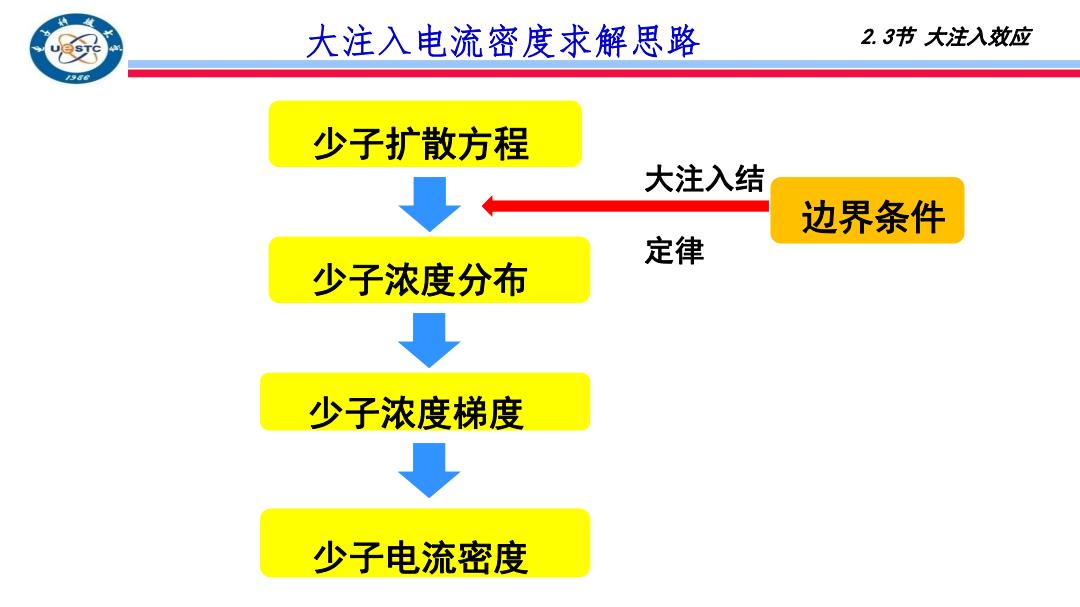
大注入电流密度求解思路 2.3节大注入效应 少子扩散方程 大注入结 边界条件 定律 少子浓度分布 少子浓度梯度 少子电流密度
少子电流密度 少子浓度梯度 少子浓度分布 少子扩散方程 边界条件 大注入电流密度求解思路 大注入结 定律 2.3节 大注入效应