《电工技术》课程教学资源（PPT课件）第5章非正弦周期电流的电路

5.1 非正弦周期交流信号 5.2 非正弦周期量的分解 5.3 非正弦周期量的有效值 5.5 非正弦周期电流电路平均功率 5.4 非正弦周期电流的线性电路的计算

团购合买资源类别：文库，文档格式：PPT，文档页数：37，文件大小：797.5KB

电工技术 dlangong 第5章非正孩周期电流的电路 5.1非正弦周期交流信号 5.2非正弦周期量的分解 5.3非正弦周期量的有效值 5.4非正弦周期电流的线性电路的计算 5.5非正弦周期电流电路平均功率总目录章目录返回上一页下一页

总目录章目录返回上一页下一页第5章非正弦周期电流的电路 5.1 非正弦周期交流信号 5.2 非正弦周期量的分解 5.3 非正弦周期量的有效值 5.5 非正弦周期电流电路平均功率 5.4 非正弦周期电流的线性电路的计算

电工技术第5章非正孩周期电流的电路本章要求： 1.会进行非正弦量的分解。 2.会进行非正弦量有效值的计算。 3.了解非正弦周期电流电路的计算方法。 4.会进行非正弦周期电流电路平均功率的计算。总目录章目录返回上一页下一页

总目录章目录返回上一页下一页第5章非正弦周期电流的电路本章要求： 1. 会进行非正弦量的分解。 2. 会进行非正弦量有效值的计算。 3. 了解非正弦周期电流电路的计算方法。 4. 会进行非正弦周期电流电路平均功率的计算

电工技术 dlangong 5.1非正孩周期交流信号前面讨论的是正弦交流电路，其中电压和电流都是正弦量。但在实际的应用中我们还常常会遇到非正弦周期的电压或电流。分析非正弦周期电流的电路，仍然要应用电路的基本定律，但和正弦交流电路的分析还是有不同之处；本章主要讨论一个非正弦周期量可以分解为恒定分量（如果有的话）和一系列频率不同的正弦量。 ◆◇◇◇◇◇00⊙00◇⊙0◇◇0◇0◇◇00◇◇0◇◇0◇◇0◇◇0◇◇◇◇0◆◇◇⊙◆ 总目录章目录返回上一页下一页

总目录章目录返回上一页下一页 5.1 非正弦周期交流信号前面讨论的是正弦交流电路，其中电压和电流都是正弦量。但在实际的应用中我们还常常会遇到非正弦周期的电压或电流。分析非正弦周期电流的电路，仍然要应用电路的基本定律，但和正弦交流电路的分析还是有不同之处；本章主要讨论一个非正弦周期量可以分解为恒定分量（如果有的话）和一系列频率不同的正弦量

电工技术 dlangong 5.1非正孩周期交流信号 1.特点按周期规律变化，但不是正弦量。 2.非正弦周期交流信号的产生 1)电路中有非线性元件； 2)电源本身是非正弦； 3)电路中有不同频率的电源共同作用。如：半波整流电路的输出信号总目录章目录返回上一页下一页

总目录章目录返回上一页下一页如：半波整流电路的输出信号 1. 特点: 按周期规律变化，但不是正弦量。 2.非正弦周期交流信号的产生 1) 电路中有非线性元件； 2) 电源本身是非正弦； 3) 电路中有不同频率的电源共同作用。 + - ui + - u0 5.1 非正弦周期交流信号 i u  t O 0 u  t O

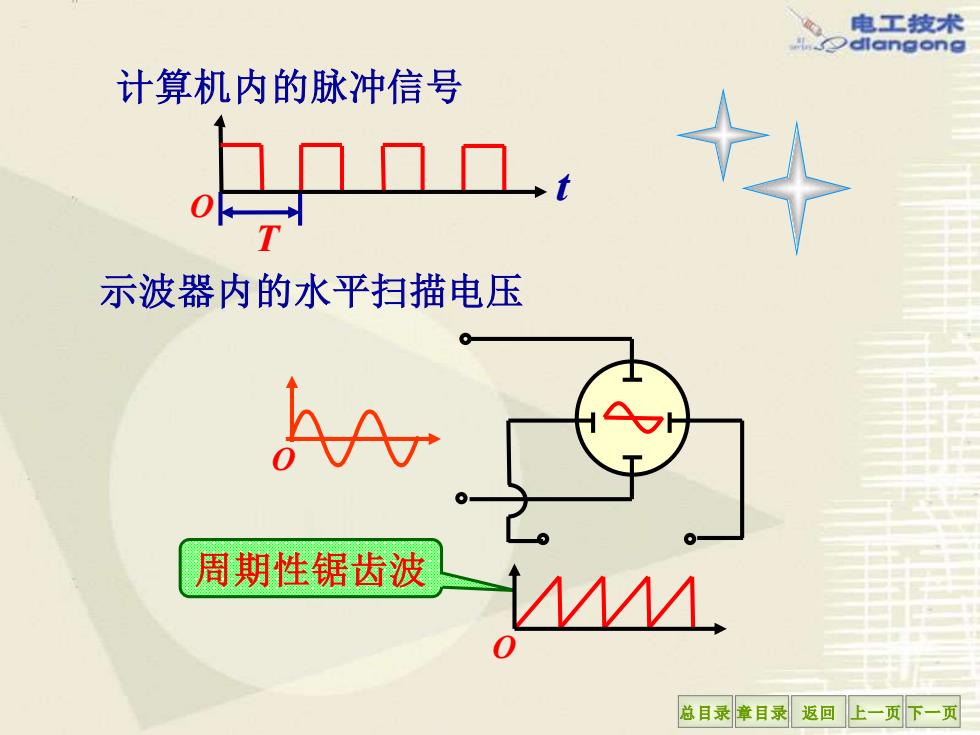
电工技术 dlangong 计算机内的脉冲信号 oc. 示波器内的水平扫描电压周期性锯齿波总目录章目录返回上一页下一页

总目录章目录返回上一页下一页示波器内的水平扫描电压周期性锯齿波计算机内的脉冲信号 O O T t O

电工技术 dlangong 晶体管交流放大电路 +U u R 交直流共存电路总目录章目录返回上一页下一页

总目录章目录返回上一页下一页晶体管交流放大电路交直流共存电路 u0 t +Ucc + - i u + - u0 + S - e t RC u ui t

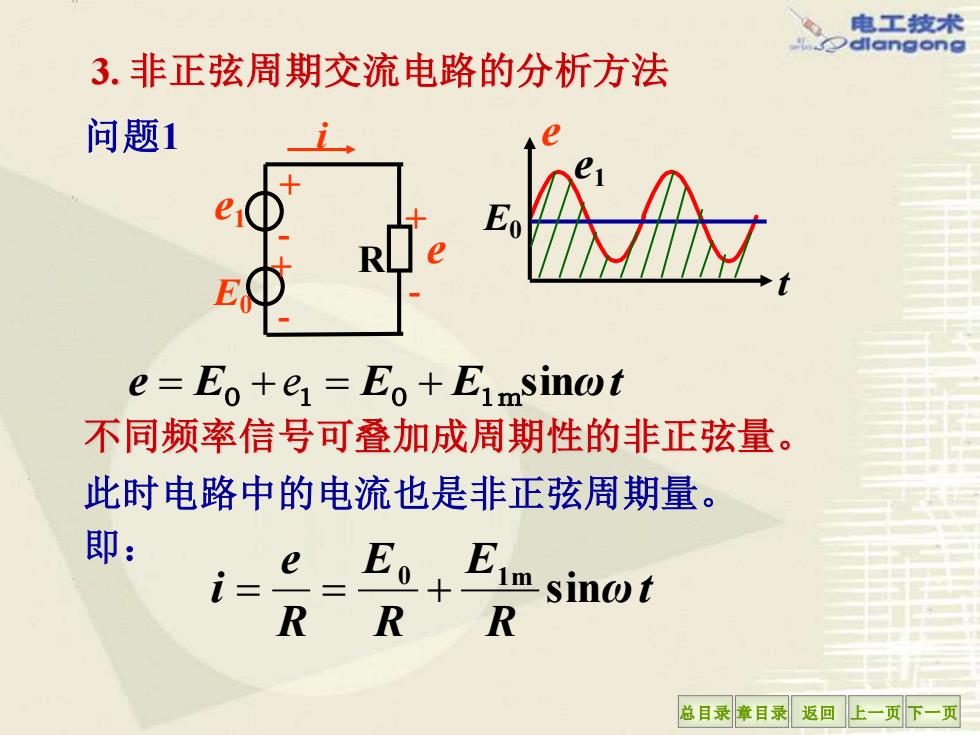
电工技术 dlangong 3.非正弦周期交流电路的分析方法问题1 0 e=Eo+e=Eo+Eimsinot 不同频率信号可叠加成周期性的非正弦量。此时电路中的电流也是非正弦周期量。即： i==Eo+Em sinot RR R 总目录章目录返回上一页下一页

总目录章目录返回上一页下一页 3. 非正弦周期交流电路的分析方法 e t E0 e1 e E E E sinωt = 0 + e1 = 0 + 1 m 问题1 i R e E0 e1 + + + - - - 此时电路中的电流也是非正弦周期量。即： ωt R E R E R e i sin 0 1 m = = + 不同频率信号可叠加成周期性的非正弦量

电工技术 dlangong 问题2：既然不同频率的正弦量和直流分量可以叠加成一个周期性的非正弦量，那么反过来一个非正弦的周期量是否也可分解为正弦分量和直流分量呢？数学上已有了肯定的答案，一切满足狄里赫利条件的周期函数都可以分解为傅里叶级数。这样就可将非正弦周期量分解为若干个正弦交流电路来求解。例：电路如图，是一周期性的非正弦量，求i一谐波分析法具体方法在5.4中介绍 R 总目录章目录返回上一页下一页

总目录章目录返回上一页下一页具体方法在5.4中介绍问题2：既然不同频率的正弦量和直流分量可以叠加成一个周期性的非正弦量，那么反过来一个非正弦的周期量是否也可分解为正弦分量和直流分量呢？数学上已有了肯定的答案，一切满足狄里赫利条件的周期函数都可以分解为傅里叶级数。这样就可将非正弦周期量分解为若干个正弦交流电路来求解。例:电路如图，u是一周期性的非正弦量，求 i 谐波分析法 i u R + -

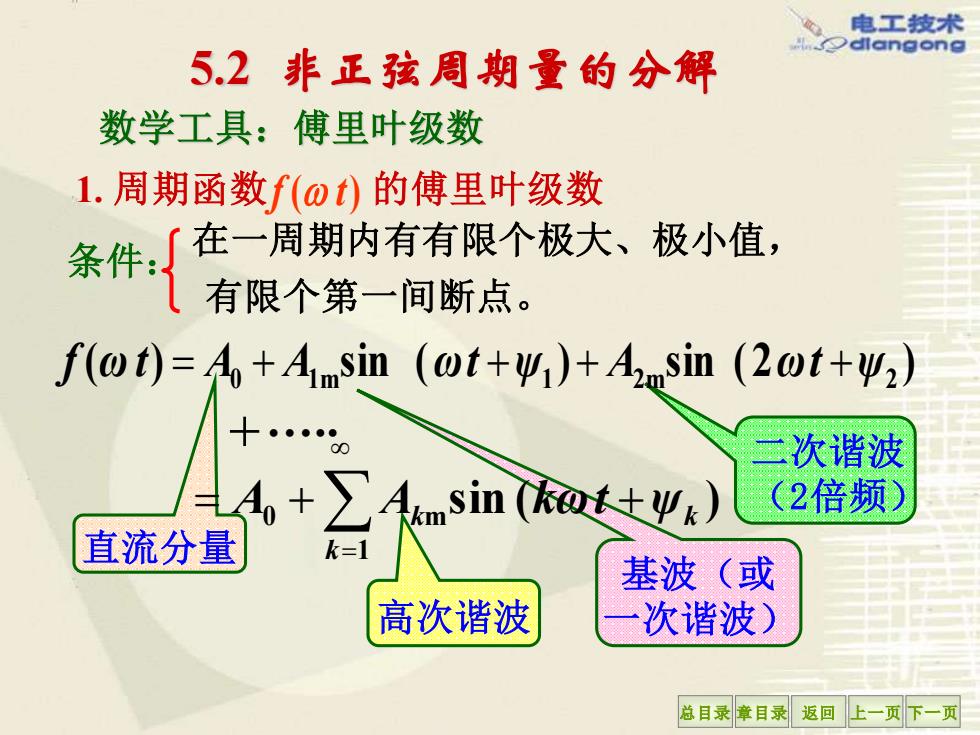
电工技术 dlangong 5.2非正孩周期量的分解数学工具：傅里叶级数 1.周期函数f(ot)的傅里叶级数条件在一周期内有有限个极大、极小值，有限个第一间断点。 f(wt)=A+A1msin(ωt+y41)+AoSin(2ωt+42) 二次诸波 +∑mSin®x) (2倍频) 直流分量 k=1 基波（或高次谐波次谐波) 总目录章目录返回上一页下一页

总目录章目录返回上一页下一页 5.2 非正弦周期量的分解基波（或一次谐波）二次谐波（2倍频）直流分量高次谐波 sin ( ) 1 0  m  = = + + k k ψk A A kωt +. ( ) sin ( ) sin ( 2 ) 0 1 m 1 2 m ψ2 f ω t = A + A ωt +ψ + A ωt + 1. 周期函数 f ( t) 的傅里叶级数数学工具：傅里叶级数条件：在一周期内有有限个极大、极小值，有限个第一间断点

电工技术周期函数 00 f(@t)=A+>Axnsin(kat+vr) K=1 Asin(kωt+业k) =Akm(sinkωt cosW&+coskωt sing） Akmcosug sin kot+Akmsiny cos kot =Bimsin kωt+Ckmcos kωt 傅里叶级数另一种形式 fwt)=A+∑B.sin kf+∑Coskt 总目录章目录返回上一页下一页

总目录章目录返回上一页下一页    =  = = + + 1 1 ( ) sin cos k k k k f ω t A B k ω t C k ω t 0 m m 周期函数 B k ω t C k ω t A ψ kω t A ψ kω t A kω t ψ k k k k k k k k k k k = + = + = + + sin cos cos sin sin cos sin cos m m m m m m ( cos kω t sinψ ) A sin (kω t ψ ) 傅里叶级数另一种形式 f A A ( k t ) K k 1 0 km  = +  sin  +  = ( t)

点击进入文档下载页（PPT格式）

共37页，可试读13页，点击继续阅读 ↓↓

点击下载（PPT格式）

浏览记录