中国科学技术大学：《数据结构及其算法》课程教学资源（课件讲稿）第2章 线性表

数据结构 线性表 第二章 线性表 主讲：张昱 重点：顺序表和链表上各种基本算 yuzhang@ustc.edu 法的实现及相关的时间性能分析 0551-3603804 难点：线性表应用的算法设计 13 273 第二章线性表 2.1线性表的类型定义 21线性表的类型定义 ·定义 2.2线性表的顺序表示和实现 n(>0)个戴摄元素的有限序列，记作(a,….n4,a) 2.3线性表的链式表示和实现 其中，4是表中数据元意，n是表长度(a-0时称为空表) 2.3.1线性链表 2.3.2循还链表 ■逻辑特征 2.3.3能态链表 n>0时 2.3.4动杰链表与静杰链袁 ·有且仅有一个“第一个"”戴排元素 2.3.5双向能意2.3.6其他袁示 。有且仅有一个“最后一个”数据元素 2.4基王链凌的算法设计 ,除第一个数据元素外，其它元素有且仅有一个直接前驱 2.5一元多项式的表示及相加 。除最后一个数据元素外，其它元素有且仅有一个直接后继 33 73 2.1线性表的类型定义-ADT List LocateElem(L,e.compare)) ,ADT Listy定义 PriorElem(L,cur_e &pre_e) 作 作结果，构地一十空的线性表虹 Des Listinsert(&L,i,e ClearList(&L) 代整壁为空味 : 装数装RuE,香F处3死 L帐 初己存在 去装无快 作铺果做衣对L的每外数描元求调用面敏vs训，一且v修出)失败，则量作失败 )ADT List 图 67 画

1/73 数据结构——线性表 主讲：张昱 yuzhang@ustc.edu 0551-3603804 2/73 重点：顺序表和链表上各种基本算 法的实现及相关的时间性能分析 难点：线性表应用的算法设计 第二章 线性表 3/73 第二章 线性表 2.1 线性表的类型定义 2.2 线性表的顺序表示和实现 2.3 线性表的链式表示和实现 2.3.1 线性链表 2.3.2 循环链表 2.3.3 静态链表 2.3.4 动态链表与静态链表 2.3.5 双向链表 2.3.6 其他表示 2.4 基于链表的算法设计 2.5 一元多项式的表示及相加 4/73 2.1 线性表的类型定义 „ 定义 n(≥0)个数据元素的有限序列,记作(a1, …ai-1, ai , ai+1,…, an) 其中，ai是表中数据元素，n 是表长度(n=0时称为空表) „ 逻辑特征 n>0时 „ 有且仅有一个“第一个”数据元素 „ 有且仅有一个“最后一个”数据元素 „ 除第一个数据元素外，其它元素有且仅有一个直接前驱 „ 除最后一个数据元素外，其它元素有且仅有一个直接后继 5/73 2.1 线性表的类型定义-ADT List „ ADT List定义 ADT List{ 数据对象：D={ai | ai∈ElemSet, i=1,2,…,n, n≥0} 数据关系：R={R1},R1={|ai-1,ai∈D, i=2,3,…,n } 基本操作： InitList(&L) 操作结果：构造一个空的线性表L DestroyList(&L) 初始条件：线性表L已存在 操作结果：销毁线性表L ClearList(&L) 初始条件：线性表L已存在 操作结果：将线性表L重置为空表 ListEmpty(L) 初始条件：线性表L已存在 操作结果：若L为空表，则返回TRUE，否则返回FALSE ListLength(L) 初始条件：线性表L已存在 操作结果：返回线性表L中数据元素的个数 6/73 2.1 线性表的类型定义 „ ADT List定义 GetElem(L, i ,&e) 初始条件：线性表L已存在，1≤i≤ListLength(L) 操作结果：用e返回L中第i个数据元素的值 LocateElem(L, e, compare( )) 初始条件：线性表L已存在，compare( )是数据元素的判定函数 操作结果：返回L中第1个与e满足关系compare( )的数据元素的位序。 若这样的元素不存在，则返回值为0 PriorElem(L, cur_e ,&pre_e) 初始条件：线性表L已存在 操作结果：若cur_e是L的数据元素，且不是第一个，则用pre_e返回它的前驱， 否则操作失败，pre_e无定义 NextElem(L, cur_e ,&next_e) 初始条件：线性表L已存在 操作结果：若cur_e是L的数据元素，且不是最后一个，则用next_e返回它的后继， 否则操作失败，next_e无定义 ListInsert(&L, i, e) 初始条件：线性表L已存在，1≤i≤ListLength(L)+1 操作结果：在L中第i个位置之前插入新的数据元素e，L的长度加1 ListDelete(&L, i, &e) 初始条件：线性表L已存在，1≤i≤ListLength(L) 操作结果：删除L的第i个数据元素，并用e返回其值，L的长度减1 ListTraverse(L, visit( )) 初始条件：线性表L已存在 操作结果：依次对L的每个数据元素调用函数visit( )。一旦visit( )失败，则操作失败 }ADT List

2.1线性表的类型定义-ADT List 2.1线性表的类型定义-例2-1 ,ADT List定义 ,基于ADT List的算法设计 ·P19 ·例2-1复设利用两个战性表La利b分别表示两个集合A和B 基本操作 (即：戴性表中的敏据元素即为果合中的成黄】，观要求一 个新的集金A一AUB。 。初始化、筛毁 ,查询：个体、整体 物入：线性表La、线性表b 。动志变化：播入、时除 输出：变化了的La 争union(&La,Lb) 处理方法：扩大线性表La,将存在于线性表Lb中而不存在于 ·重点掌提以下三个基本操作 线性表La中的敏搭元素辑入到铁性表La中去。 。GetElem(L,i,&e) 8 步骤： ListInsert(&L,i,e) ~1,从线性表b中依次取得每个数据元素 ListDelete(&L,i,&e) LocateElem 2,依值在线性表La中进行查访 注意：接口的形式可以略有变化，如e=GetElem(L,) 不存在，则插入之 7 回 1的 73 回 2.1线性表的类型定义-例2-1 21线性表的类型定义削2.2 void union(List &La,List Lb){ ,基于ADT List的算法设计 /∥将所有在城性表b中不在La中的数元素入到a中 La_len ListLength(La); 。例2-2巴加旋性兼La布Lb中的数据元素妆值摔递减有序掉 e是变◆ Lb_Jen=ListLength(b:/求，性囊的长度 列，要求将La不Lb归并成一个新的战性表L,且Lc中的数据 调用时不 元素仍：值非递减有序神列。 加&符号 =i<=地e;it+) GetElem(b,同：/取Lb中第i个数W元肃减皓e 输入：线性表La、线性表b(均按值丰道减有序排列) if(LocateElem(La.e.eoual)) 输出：Lc(拨值非道减有序排列merge(La,Lb,&Lc) /La中不存在和e相同的元豪，则插入之 处理方法：：La和Lb均按值非通减有序排列 ListInsert(La,++La_len,e); ∴设置两个位置指示器和j,分别指肉L和Lb中的某个元 )/union 素，初始均指向第1个。LC初始化为空表。 比较和所指肉的元景a和bj,进取值小的插入到Lc的尾部， T(na,nb)=O(b*na),na、nb表示La表和Lb表的长度 并使相应的位置指示卷向后移。 算法：算法2.2P21 9/73 图 10y73 图 2.1线性表的类型定义-例2-2 2,1线性表的类型定义-例2-2 void MergeList(List La,List Lb,List &Lc){ a和Lb中的元素教值非 /归La和Lb得到断的，性表Lc,Lc的元素拔值非递减排列。 ListInsert(Lc,++k,ai); InitList(Lc); i=j=1;k=0: while (j<=Lb_len){ La_len ListLength(La); GetElem(Lb,j++,bj); Lb len ListLength(Lb): ListInsert(Lc,++k,bj); while ((i<=La_len)&&(j<=Lb_len)){ a和b均非空 }//MergeList GetElem(La,i,ai);GetElem(Lb,j,bj); if (ai<=bj){ ListInsert(Lc,++k,ai);++i; T(na,nb)=O(na+nb) ListInsert(Lc,++k,bj);++j; 1/ 图 12万 图

7/73 2.1 线性表的类型定义-ADT List „ ADT List定义 „ P19 基本操作 „ 初始化、销毁 „ 查询：个体、整体 „ 动态变化：插入、删除 „ 重点掌握以下三个基本操作 „ GetElem(L, i ,&e) „ ListInsert(&L, i, e) „ ListDelete(&L, i, &e) 注意: 接口的形式可以略有变化,如 e = GetElem(L, i) 8/73 2.1 线性表的类型定义-例2-1 „ 基于ADT List的算法设计 „ 例2-1 假设利用两个线性表La和Lb分别表示两个集合A和B （即：线性表中的数据元素即为集合中的成员），现要求一 个新的集合A＝A∪B。 输入：线性表La、线性表Lb 输出：变化了的La Îunion(&La, Lb) 处理方法：扩大线性表La，将存在于线性表Lb中而不存在于 线性表La中的数据元素插入到线性表La中去。 步骤： 1．从线性表Lb中依次取得每个数据元素; 2．依值在线性表La中进行查访; 3．若不存在，则插入之。 算法：算法2.1 P20 ListLength GetElem LocateElem ListInsert 9/73 2.1 线性表的类型定义-例2-1 void union(List &La, List Lb) { // 将所有在线性表Lb中但不在La中的数据元素插入到La中 La_len = ListLength(La); Lb_len = ListLength(Lb); // 求线性表的长度 for (i = 1; i <= Lb_len; i++) { GetElem(Lb, i, e); // 取Lb中第i个数据元素赋给e if(!LocateElem(La, e, equal)) // La中不存在和e相同的元素，则插入之 ListInsert(La, ++La_len, e); } } // union T(na, nb) =O(nb*na), na、nb表示La表和Lb表的长度 e是变参, 调用时不 加&符号 10/73 2.1 线性表的类型定义-例2-2 „ 基于ADT List的算法设计 „ 例2-2 已知线性表La和Lb中的数据元素按值非递减有序排 列，要求将La和Lb归并成一个新的线性表Lc，且Lc中的数据 元素仍按值非递减有序排列。 输入：线性表La、线性表Lb(均按值非递减有序排列) 输出：Lc(按值非递减有序排列) Îmerge(La, Lb, &Lc) 处理方法：∵La和Lb均按值非递减有序排列 ∴设置两个位置指示器i和j，分别指向La和Lb中的某个元 素，初始均指向第1个。Lc初始化为空表。 比较i和j所指向的元素ai和bj，选取值小的插入到Lc的尾部， 并使相应的位置指示器向后移。 算法：算法2.2 P21 11/73 2.1 线性表的类型定义-例2-2 void MergeList(List La, List Lb, List &Lc) { // 已知线性表La和Lb中的元素按值非递减排列。 // 归并La和Lb得到新的线性表Lc，Lc的元素按值非递减排列。 InitList(Lc); i = j = 1; k = 0; La_len = ListLength(La); Lb_len = ListLength(Lb); while ((i <= La_len) && (j <= Lb_len)) { // La和Lb均非空 GetElem(La, i, ai); GetElem(Lb, j, bj); if (ai <= bj) { ListInsert(Lc, ++k, ai); ++i; }else { ListInsert(Lc, ++k, bj); ++j; } } 12/73 2.1 线性表的类型定义-例2-2 while (i <= La_len) { GetElem(La, i++, ai); ListInsert(Lc, ++k, ai); } while (j <= Lb_len) { GetElem(Lb, j++, bj); ListInsert(Lc, ++k, bj); } } // MergeList T(na, nb) =O(na+nb)

2.1线性表的类型定义-结论 2.2线性表的顺序表示和实现 。结论 ▣定义：用一组地址连线的存储单元依火存储线 ·使用不同的算法策略，可以得到不同时间复 性表中的数据元素 杂度的算法 ■特点：逻枰上相邻，物理上也相邻。随机存取 ,输入线性表的特征会形响算法的策略 （是否有序？…) 逻料序号12345 6 陈述问 。输出线性表的特征会形响算法的策略 688970674078 题时用 (是否有序？…) C数组下标012345 13n 回 1W万 图 2.2-顺序表的存储 2.2-顺序表类型定义（方案一） 假设每个元素占用个存储单元，则元素的存 顺序表定义 储位置： ·方案一 #define LIST_SIZE 100 LOC(a)=LOC(a)+ typedef struct{ LOC(a)=LOC(aj)+(i-1)*I ElemType elem[LIST_SIZE]; 严存情空何1 int length; 胪当前长度 12 …i )SqList_static; an 评价： ↑ 1LSTS1ZE进小，则会号顺序表上道： a+(n-1)*I idle 2)LIST SIZE过大，则女导数空间的利用率不高 15/73 图 13 图 2.2-顺序表类型定义（方案二） 2.2C中的动态分配与释放函数 方案二 C中的动态分配与释放函数 void *malloc(unsigned int size) 大小为心的韩底空间，将请空间的起地 typedef struct( ElemType 'elem; ”存储空间的基址 地址赋给p: int length: 产当前长度 free(void *p) int listsize: :当前分配的存储客量1 回收p所指向的结点空间： )SqList; .void *realloc(void *p,unsigned int size) 将D所描向的已分配内存区的大小改为size,sizc 该方案解决方案一中的上滥"问圆和“空间利用率不高问 愿，但是有时间和空间代价的。 分配成助示组 可以比原分配的空间大或小。 )必须记藏当前做性表的实际分配的空间大小： 当 引当或不再使用时，应放其所占的空间： 3)要夹现的语言能展供空间的动本分配与放理， 177万 图

13/73 2.1 线性表的类型定义-结论 „ 结论 „ 使用不同的算法策略，可以得到不同时间复 杂度的算法 „ 输入线性表的特征会影响算法的策略 （是否有序？…） „ 输出线性表的特征会影响算法的策略 （是否有序？…） 14/73 2.2 线性表的顺序表示和实现 „ 定义：用一组地址连续的存储单元依次存储线 性表中的数据元素 „ 特点：逻辑上相邻，物理上也相邻。随机存取 68 89 70 67 40 78 逻辑序号 1 2 3 4 5 6 C数组下标 0 1 2 3 4 5 陈述问 题时用 15/73 2.2 -顺序表的存储 假设每个元素占用l个存储单元，则元素的存 储位置： LOC(a i+1) = LOC( a i )+l LOC(a i ) = LOC(a1)+(i-1)*l a1 a2 … a i …… … an 1 2 … i ……… n a a+l … a+(i-1)*l … … … a+(n-1)*l idle 16/73 2.2 –顺序表类型定义(方案一) „ 顺序表定义 „ 方案一 #define LIST_SIZE 100 typedef struct{ ElemType elem[LIST_SIZE]; /* 存储空间*/ int length; /* 当前长度*/ }SqList_static; 评价： 1)LIST_SIZE过小，则会导致顺序表上溢； 2) LIST_SIZE过大，则会导致空间的利用率不高 17/73 2.2 –顺序表类型定义(方案二) „ 方案二 #define LIST_INIT_SIZE 100 /* 存储空间的初始分配量*/ #define LISTINCREMENT 10 /* 存储空间的分配增量 */ typedef struct{ ElemType *elem; /* 存储空间的基址 */ int length; /* 当前长度 */ int listsize; /* 当前分配的存储容量 */ }SqList; 该方案解决方案一中的“上溢”问题和“空间利用率不高”问 题 ，但是有时间和空间代价的 。 1) 必须记载当前线性表的实际分配的空间大小； 2) 当线性表不再使用时，应释放其所占的空间； 3) 要求实现级的语言能提供空间的动态分配与释放管理。 18/73 2.2 –C中的动态分配与释放函数 „ C中的动态分配与释放函数 „ void *malloc(unsigned int size) 生成一大小为size的结点空间，将该空间的起始 地址赋给p； „ free(void *p) 回收p所指向的结点空间; „ void *realloc(void *p, unsigned int size) 将p所指向的已分配内存区的大小改为size，size 可以比原分配的空间大或小。 old p new size 起址 返回 回收 分配成功示例

2.2-C中的动态分配与释放函数 2.2一基本操作的实现（宏与Status) C中的动态分配与释放函数 ■基本操作的实现 void *malloc(unsigned int size) P10 生成一大小为s立的站点空间，将被空间的起地 地址赋给p: /体函数结果状春代码 #define TRUE 1 free(void *p) 回收p所指询的结点空间： #define FALSE #define OK 1 void *realloc(void *p,unsigned int size) #define ERROR 0 特p所指向的已分配内存区的大小改为size,size #define INFEASIBLE -1 分配失败示 可以比原分乖的空间大或小。 #define OVERFLOW -2 条温 /体函数结果状态类型，其值为上述的状本代码 typedef int Status; 172 囵 20y3 图 2.2-基本操作的实现(InitList_Sq) 主2.2-基本操作实现(LocateElem-.s)刘 ■基本操作的实现 ■基本操作的实现 ,°化Status InitList_Sq(SqList&L) ,求表长L.length Status InitList_Sq(SqList &L){ ∥构造一个空的线性表L ,取第i个元素L.elem[i-1](0=子-L.e4em0]=L.elem-1j/∥盾w 入e L.eemt-1】=ei/算个元常存放在L.elem[i-1]中，胞地下标为0 L.length Llength+1; 48y 123456789 ,法的位置：i1L.length+1 。上滥及处理： 1523464816571064 。上提搜生的条并：LlengthL.lists位e, 22/7万 图

19/73 2.2 –C中的动态分配与释放函数 „ C中的动态分配与释放函数 „ void *malloc(unsigned int size) 生成一大小为size的结点空间，将该空间的起始 地址赋给p； „ free(void *p) 回收p所指向的结点空间; „ void *realloc(void *p, unsigned int size) 将p所指向的已分配内存区的大小改为size，size 可以比原分配的空间大或小。 old p 返回 空间不够, NULL 分配失败! 分配失败示例 20/73 2.2 –基本操作的实现(宏与Status) „ 基本操作的实现 P10 /* 函数结果状态代码 */ #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define INFEASIBLE -1 #define OVERFLOW -2 /* 函数结果状态类型，其值为上述的状态代码 */ typedef int Status; 21/73 2.2 –基本操作的实现(InitList_Sq) „ 基本操作的实现 „ 初始化 Status InitList_Sq(SqList &L) Status InitList_Sq( SqList &L) { // 构造一个空的线性表L L.elem = (ElemType *) malloc(LIST_INIT_SIZE*sizeof(ElemType)); if ( L.elem == NULL ) exit(OVERFLOW); // 存储分配失败 L.length = 0; // 空表长度为0 L.listsize = LIST_INIT_SIZE; // 初始存储容量 return OK; } // InitList_Sq 22/73 2.2 –基本操作实现(LocateElem_Sq) „ 基本操作的实现 „ 求表长 L.length „ 取第i个元素 L.elem[i-1] (0= i; j--) L.elem[j] = L.elem[j-1]; // 后移 L.elem[i -1] = e; //第i个元素存放在L.elem[i-1]中，起始下标为0 L.length = L.length+1; „ 合法的位置：i:1..L.length+1 „ 上溢及处理： „ 上溢发生的条件：L.length≥L.listsize， „ 处理：先申请一个有一定增量的空间：申请成功则原空间的元素复制 到新空间，修改L.listsize，再进行插入工作；否则报错退出

2.2-插入操作的实现（算法） 2.2-插入操作的实现（算法分析） 77时u nepe 时闯复杂度 if (iLlength +1) return ERROR; 。频次最高的操作：移动元豪 /上避时增加空间的分配 ,上漫时，空间的再分配与复制(reoc操作分摊到每次领入操作中 if(Llength >Llistsize){ 。若能性表的长度为■，则： ,量好品推入位置为+1，此时无须暮助元素，T)-01) 为什么量引 (ElemType)al(Lele (Llistsize+LIST INCREMENT 是经品描入位量为1，此时须移动▣个元素，T(@)一0时 入newbase? (ElemType)); if newbase==NULL exit(OVERFLOW); ,平垃品假设为在第个元素之前捕入一个元素的振率， elem newbase; 空间分配失败 Llistsize+=LISTINCREMENT; 箱入时带动次最的明道值：E。=艺P,口-1+) 时，蓬免将原 川地止失 //麵入元康 等振率时，可 】+ for (j=L.length;j>=i;j--)L.elem[j]=Lelem[j-1]; Lelem[i-1]=e Llength++; p,+1 T时-0 return OK; ,空间复杂度S)-01) 25/73 回 273 图 22-刷除操作的实现 2.2-删除操作的实现（分析设计） 基本操作的实现 ·测除操作一算法设计（算法2.5） ■副除操作 。数：顺序表&L、副除位量 Status ListDelete_Sq(SqList &L int i,ElemType &e) ·除分折： 。去辣幕i个元章，则原来第+1-L.kg山个敏据元囊必须前 12345678 移，以服整第个位置 15234616571064. 。前移的顺序是从靠行+1元豪开增，是个住前修 for (j-i:jL.length return ERROR; 连品副除位量为1，此时须黄移1个元素， /剔除 T(n)-O(n): ,亚均况：假设为测膝靠个元豪的振率，则： for (j=i;j<L.length ;j++) 汇除时移动次数的厕望值： L.elem[j-1]L.elem[j]; E-2a-0 L.length--; return OK; T-0) ,空间复杂度S(a)-0山 297万 图 307万 图

25/73 2.2 –插入操作的实现(算法) Status ListInsert_Sq( SqList &L, int i, ElemType e) { // 位置合法性的判断 if ( iL.length +1 ) return ERROR; // 上溢时增加空间的分配 if( L.length >= L.listsize){ newbase = (ElemType *) realloc(L.elem, (L.listsize+ LISTINCREMENT)*sizeof(ElemType)); if ( newbase == NULL ) exit(OVERFLOW); L.elem = newbase; L.listsize += LISTINCREMENT; } // 插入元素 for ( j = L.length; j >= i; j--) L.elem[j] = L.elem[j-1]; L.elem[i-1] = e; L.length++; return OK; } 为什么要引 入newbase? 空间分配失败 时，避免将原 空间地址丢失! 26/73 2.2 –插入操作的实现(算法分析) „ 时间复杂度 „ 频次最高的操作：移动元素 „ 上溢时，空间的再分配与复制(realloc操作)分摊到每次插入操作中 „ 若线性表的长度为n，则： „ 最好情况：插入位置i为n+1，此时无须移动元素，T(n)=O(1); „ 最坏情况：插入位置i为1，此时须移动n个元素， T(n)=O(n); „ 平均情况：假设pi为在第i个元素之前插入一个元素的概率， 则： 插入时移动次数的期望值： 等概率时，即 ， ∴ T(n) = O(n) „ 空间复杂度 S(n) = O(1) ∑ + = = − + 1 1 ( 1) n i is i E p n i 1 1 + = n pi 2 ( 1) 1 1 1 1 n n i n E n i is − + = + = ∑ + = 27/73 2.2 –删除操作的实现 „ 基本操作的实现 „ 删除操作 Status ListDelete_Sq(SqList &L, int i, ElemType &e) 15 23 46 16 57 10 64 …… 1 2 3 4 5 6 7 8 16 删除 e 0 1 2 3 4 5 6 7 i 15 23 46 57 10 64 …… 1 2 3 4 5 6 7 28/73 2.2 –删除操作的实现(分析设计) „ 删除操作——算法设计(算法2.5) „ 参数：顺序表&L、删除位置i „ 删除分析： „ 去掉第i 个元素，则原来第i+1~L.length个数据元素必须前 移，以覆盖第i个位置; „ 前移的顺序是从第i+1元素开始，逐个往前移 for ( j = i; j L.length ) return ERROR; // 删除 for ( j = i; j < L.length ; j++) L.elem[j-1] = L.elem[j]; L.length--; return OK; } 30/73 2.2 –删除操作的实现(算法分析) „ 时间复杂度 „ 频次最高的操作：移动元素 „ 若线性表的长度为n，则： „ 最好情况：删除位置i为n，此时无须移动元素，T(n)=O(1); „ 最坏情况：删除位置i为1，此时须前移n-1个元素， T(n)=O(n); „ 平均情况：假设qi为删除第i个元素的概率，则： 删除时移动次数的期望值： 等概率时，即 ， ∴ T(n) = O(n) „ 空间复杂度 S(n) = O(1) ∑= = − n i de i E q n i 1 ( ) n qi 1 = 2 1 ( ) 1 1 − = ∑ − = = n n i n E n i de

2.2-算法设计（例2-1,2-2） 2.3线性表的链式表示和实现 基于顺序表的算法设计 ■单链表 例2-1和例2-2 ·循环链表 。基本操作在顺序表中的实现 。istLength(La) La.length ·静态链表 GetElem(Lb,I,e) e=Lb.elem[l-1]; ·静态链表V5.动态链表 LocateElem(La,e,equal) ListInsert(La,++La_len,e)La.elem[La.length++]=e; ·双向链表 ·基于顺序表实现例2-1和例2-2 善本操作的简单管换，针对例2-2得到P26算法2.7 ■其他表示 31V73 回 3划3 图 2.3.1单链表-定义 2.3.1单链表-定义 。单链表 。链表定义 ·质序映像的码点 ·蜡点表操元素的存储映德，包括数罐和潮罐（其信惠米为 指所或前) ,空间利用率不高（预先按最大空间分配） 头指针链表存取的开始，空NLL最后一个塘点的指 。表的容量不可扩充（针对顺序表的方案一） 春情地址 数操城烟针城 。即使表的客量可以扩充（针对顺序表的方案二），由于其 1 工 空间再分配和复制的开销，也不允许它频黛地使用 7 QIAN 13 。插入或副障时蓄移动大量元素 头指针 SUN :链表定义 31 19 WANG NULL WU 37 。特点 3 ZHAO 迎操上相邻的元章，物通上未必相邻，非题机存取 37 ZHENG 19 33/73 图 ZHOU 25 图 2.3.1单链表-定义和基本操作 2.3.1单链表-取第i个元素 ·能表定义 ,皇慕i个元意GetElem_L(LinkList L,intL,ElemType&e) typedef struct LNode{ 位量i、取得的第个元素&e ElemType data; /食船故 算法：带头结点的单能表中取第个元素 struct LNode*next//后向指针城 Status GetElem_L(LinkList L int i,ElemType &e){ >LNode,*LinkList; /川表示当前P所指向的元豪在线性表中的位序 p=出j=1y 。基本操作的实现 须欲录高的操作 while (jnext:计+/后移指针并计 ,插△排ListInsert_L(LinkList&L,lntl,ElemType e) 度为i-1； ,壁並山stDelete_L(LinkList&L,intl,ElemType&e) f(p==NULL IIj>)return ERROR;/第个元素不存在 e=p->data;/取第i个元素 ,创度差熊CreateL以(LinkLis过&L) return OK; 马清法 图 T(n)=0(n) 35/7 图

31/73 2.2 –算法设计(例2-1,2-2) „ 基于顺序表的算法设计 例2-1和例2-2 „ 基本操作在顺序表中的实现 „ ListLength(La) La.length „ GetElem(Lb, i, e) e = Lb.elem[i-1]; „ LocateElem(La, e, equal) „ ListInsert(La, ++La_len, e) La.elem[La.length++] = e; „ 基于顺序表实现例2-1和例2-2 基本操作的简单替换，针对例2-2得到P26算法2.7 32/73 „ 单链表 „ 循环链表 „ 静态链表 „ 静态链表 vs. 动态链表 „ 双向链表 „ 其他表示 2.3 线性表的链式表示和实现 33/73 „ 单链表 „ 顺序映像的弱点 „ 空间利用率不高（预先按最大空间分配） „ 表的容量不可扩充（针对顺序表的方案一） „ 即使表的容量可以扩充（针对顺序表的方案二），由于其 空间再分配和复制的开销，也不允许它频繁地使用 „ 插入或删除时需移动大量元素 „ 链表定义 „ 特点 逻辑上相邻的元素，物理上未必相邻；非随机存取 2.3.1 单链表–定义 34/73 „ 链表定义 „ 结点-数据元素的存储映像，包括数据域和指针域（其信息称为 指针或链） „ 头指针-链表存取的开始 ；空(NULL)-最后一个结点的指针 2.3.1 单链表–定义 数据域 指针域 LI 43 QIAN 13 SUN 1 WANG NULL WU 37 ZHAO 7 ZHENG 19 ZHOU 25 存储地址 1 7 13 19 25 31 37 43 31 头指针 35/73 „ 链表定义 typedef struct LNode{ ElemType data; //数据域 struct LNode *next;//后向指针域 }LNode, *LinkList; „ 基本操作的实现 „ 取第i个元素 GetElem_L(LinkList L, int i, ElemType &e) „ 插入操作 ListInsert_L(LinkList &L, int i, ElemType e) „ 删除操作 ListDelete_L(LinkList &L, int i, ElemType &e) „ 创建单链表 CreateList_L(LinkList &L) „ 头插法 尾插法 2.3.1 单链表–定义和基本操作 36/73 „ 取第i个元素GetElem_L(LinkList L, int i, ElemType &e) 参数：链表L、位置i、取得的第i个元素&e 算法：带头结点的单链表中取第i个元素 Status GetElem_L( LinkList L, int i, ElemType &e) { // j表示当前p所指向的元素在线性表中的位序 p = L; j = 1; while ( j next; j++; // 后移指针并计数j } if ( p == NULL || j > i) return ERROR;// 第i个元素不存在 e = p->data; // 取第i个元素 return OK; } 2.3.1 单链表–取第i个元素 T(n) =O(n) 频次最高的操作 当1≤i≤表长n时, 频度为i-1; 否则为n

2.3.1单链表-头结点的引入 2.3.1单链表-插入操作（分析设计） ,播入振作ListInsertL(LinkList&L,tntl,ElemType e】 ,单链表中是否引入头结，点？ 【设计思路】 。无头站点 相关塘点：a,和a 儿D-国的 点的示：引入指针变量LinkList p; 空表时，L为NULL :能表结点的指针城是推向读姑旅的直捷后健 第一个结点无前驱结点，只能通过某指针变量来指向，如L: ∴，当p指向a时，a可用p->next)表示 其余结点均有前驱结点，放可通过其直接前配结点的ext城 关整步： 来指向，即->next; ①液p推向a:暗点> P 5 '如a·-F p≠NULL,则 ▣有头站点 分操作 ②s=(LinkList -0 空表时，L指向一结点（称为头结点） of(LNode)); e 第一个结点和其食结点均可线一表示为其直接前驱结点的 ®s->data=e; ④s->next=p->next ③ next城所指向的结点，即. ->next. p->next =s; 3773 回 3/3 T(n)=0(n) 图 2.3.1单链表-插入操作（分析设计） 2.3.1单链表插入操作（算法） .入摄作ListInsert_(L LinkList&L,intl,ElemType e) 【有头纳点的算法】 【设计恩席】 Status ListInsert(LinkList&L,inti,ElemType eX 桶关填点：a1和a /有头结点，无须对为1的横入位置作特躁处理 第点的衰示，引入指计变量LinkList p: p=L:j=0://对Pj初始化：多p为L的第j个结点 while(p!=NULL &jnext; j+ /1零找第-1个结点的位量 当p指向a1时，a可用(p->next)表示 关敏步源： 9 if(p==NULL II j>i-1) PNULL,则 正于 return ERROR; /川i小于1或大于表长 ②s=(LinkList)malloc 0 s=(LinkList)mallod(sizeof(LNode)/I生成新结点 if (s==NULL) (sizeof(LNode)); exit(OVERFLOW:/空间分配不成动，报幢返园 s>data=e 0 s>daa=写s>net=p->next入中 ③q=p->next p->next= ③p->next=5 return OK; s->next =q; 3/73 图 40y72 图 2.3.1单链表插入操作（算法） 2.3.1单链表插入操作（小结） 【无头铺点的算法】 Status ListInsert(LinkList &L int i,ElemType eX /无头俯点，须对为1的插入位量作特珠处理 ■链表操作的算法设计小结 if (i=1X s=(LinkList)malloc(sizeof(Node:/∥生R事铺点 ·采用画图法 Cown:1宅分不热：带运日 。先画初始状态 升金铁 s>data■e时s->net=山/瓶) ,画出结果状态 L=s; 。标出各操作步骤的次序 P二升精架的热线8集的粥a 次序的确定方法： ,根据操作步廉之间的依被关系 随意确定一种次序信惠的丢失 return OK; 在信息丢失前，增加操作步腰以暂存将要丢失的信意 游活结点和有头结在入祛上的不 。假设一些条件：有无头结点 图 42万 图

37/73 „ 单链表中是否引入头结点？ „ 无头结点 空表时，L为NULL 第一个结点无前驱结点,只能通过某指针变量来指向，如L； 其余结点均有前驱结点，故可通过其直接前驱结点的next域 来指向，即……->next； „ 有头结点 空表时，L指向一结点(称为头结点) 第一个结点和其余结点均可统一表示为其直接前驱结点的 next域所指向的结点，即……->next。 2.3.1 单链表–头结点的引入 a1 a2 L an ^ a1 an ^ L 38/73 „ 插入操作ListInsert_L(LinkList &L, int i, ElemType e) 【设计思路】 相关结点：ai-1和ai 结点的表示：引入指针变量LinkList p; ∵链表结点的指针域是指向该结点的直接后继 ∴当p指向ai-1时，ai 可用*(p->next)表示 关键步骤： ①使p指向ai-1 结点 p≠NULL，则 ② s = (LinkList)malloc (sizeof(LNode)); ③ s->data = e; ④ s->next = p->next; ⑤ p->next = s; 2.3.1 单链表–插入操作(分析设计) 耗时间！ T(n) =O(n) ai-1 ai p 1 2 s e 3 分析操作 5 4 间的依赖关 系，确定操 作的次序！ 39/73 „ 插入操作ListInsert_L(LinkList &L, int i, ElemType e) 【设计思路】 相关结点：ai-1和ai 结点的表示：引入指针变量LinkList p; ∵链表结点的指针域是指向该结点的直接后继 ∴当p指向ai-1时，ai 可用*(p->next)表示 关键步骤： ①使p指向ai-1 结点 p≠NULL，则 ② s = (LinkList)malloc (sizeof(LNode)); ③ s->data = e; 3' q=p->next; ④ p->next = s; ⑤ s->next = q; 2.3.1 单链表–插入操作(分析设计) ai-1 ai p 1 2 s e 3 4 5 信息丢失： ai 的位置？ q 3' 随意给 出操作的 次序！ 40/73 【有头结点的算法】 Status ListInsert(LinkList &L, int i, ElemType e){ // 有头结点，无须对i为1的插入位置作特殊处理 p = L; j = 0; // 对p,j初始化; *p为L的第j个结点 while( p != NULL && jnext; j++; // 寻找第i-1个结点的位置 } if( p == NULL || j>i-1) return ERROR; // i小于1或大于表长 s = (LinkList )malloc(sizeof(LNode)); // 生成新结点 if ( s == NULL ) exit(OVERFLOW); // 空间分配不成功，报错返回 s->data = e; s->next = p->next; // 插入L中 p->next = s; return OK; } 2.3.1 单链表–插入操作(算法) 41/73 【无头结点的算法】 Status ListInsert(LinkList &L, int i, ElemType e){ //无头结点，须对i为1的插入位置作特殊处理 if ( i==1){ s = (LinkList )malloc(sizeof(LNode)); // 生成新结点 if ( s == NULL ) exit(OVERFLOW); // 空间分配不成功，报错返回 s->data = e; s->next = L; // 插入到链表L中 L = s; // 修改链头指针L }else{ p = L; j = 1; // 对p,j初始化; *p为链表的第j个结点 …… //同有头结点算法的处理：①~⑤ } return OK; } 【思考】对比无头结点和有头结点在插入算法上的不同， 分析其中的原因。 2.3.1 单链表–插入操作(算法) 42/73 2.3.1 单链表–插入操作(小结) „ 链表操作的算法设计小结 „ 采用画图法 „ 先画初始状态 „ 画出结果状态 „ 标出各操作步骤的次序 次序的确定方法： „ 根据操作步骤之间的依赖关系 „ 随意确定一种次序Î信息的丢失 在信息丢失前，增加操作步骤以暂存将要丢失的信息 „ 假设一些条件: 有无头结点…

2.3.1单链表-删除操作（分析设计） 2.3.1单链表-创建操作 慰脍振作ListDelete_L(LinkList&L,intl,ElemType&e) .创建单链表CreateList_L((LinkList&L) 【设计恩略】 相关结点：a1、a和a, 。头插法 铺点的表示：引入指针变量山nk山istP 链表结点的指针娘是指向该塘点的直接后壁 新结点插入 当p指a时，a可用*(p->next)表示， 到线性表中的第1 a4可用*(p->next> 个结点之前. ① 关量步■： 了花时同！ e 花p推向a随减 p->nextNULL,则 0年道 ,思描法 a■D->net 8 ext =p->next->next; a□#aG 新结点插入 6IO 到线性表中最后1 {②p T(n)=0(n) 个结点之后， 47 回 e- 4W方 图 2.3.1单链表-头插法创建 2.3.1单链表-尾插法创建 ,头插法（算法2.11，P30) ,品描法 思想：每次将特插结点*s插入到第一个结点之前：当有头结点时， 思想：特输结点描入到最后一个结点之后。 特插结点也可视为描入到第0个结点（头结点）之后。 播入步丽：①获得最后一个结点的位置使即指向该储点 摇入步骤：以单链表中有头结点为例，单个结点的构造和蝴入步躁如 p->next =(LinkList)malloc(sizeof(LNode)); 下：①s=(LinkList)malloc(sizeof(LNode): ②scanf(&s->data);③s>next=L->next,④L->next=s 算法分新，由上可谱出每次描入一个结点所需的时间为0(1) 算法分析：要想扶取最后一个结点的位置，必须从头指针开始顺 式链撞套链麦的全部结点，该过四的时间复杂度是 ∴头插法创建单楚表的时间复杂度T()=0() ()。如果每次插入都按此 方法获取最后一个结点的位 知+一D一→ 置，则整个创魔算法的时间 复来度为T(n)=0(n2). 工 45/73 图 3 图 2.3.2循环链表 2.3.3静态链表 ■循环链表 ■静态链表(P31~34) ·问愿1 如何从一个结，旅出发，访问到能表中的全部结点？ ·问题： 循环表 ,若语言不支持指针类型，能有链式存储吗？ 可以借用语言中的数姐来表示能表—普态链衰 ·问愿2 数组元素（数据元素的值、描示器） 结点 如何在0(1)时间内由能表指针访问到第一个结燕和 最后一个站点？ ,类型定义 一头指针表示/尾指针表示 #define MAXSIZE 1000 typedef struct( ,与单链表在基本操作的实现上的差异 ElemType data; 如链表的创 int cur; 管代动态链表结点中的指针城 痛环结束泰件的判断：p--NULL>p一L )component,SLinkList[MAXSIZE]; 47 可图 图

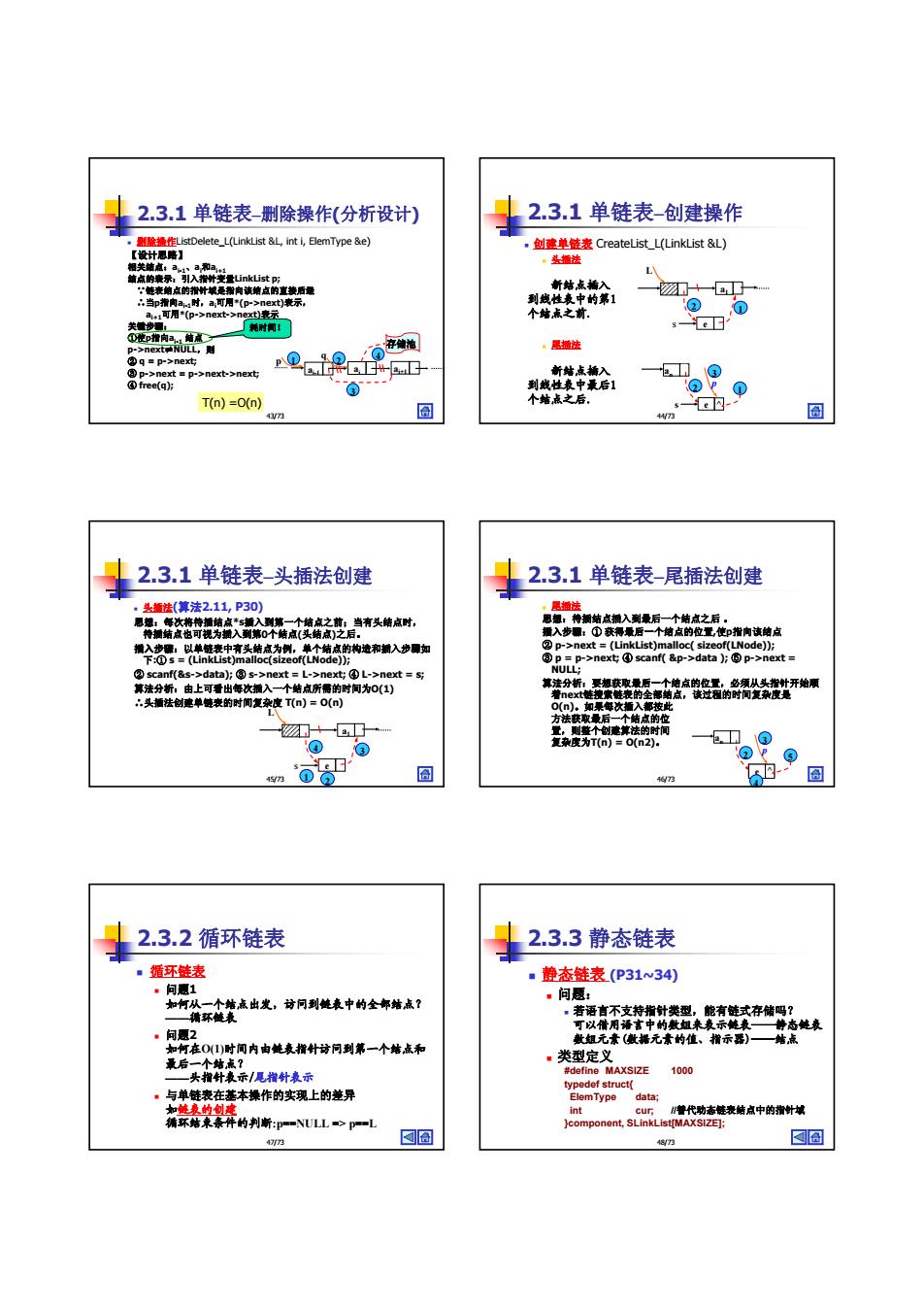
43/73 „ 删除操作ListDelete_L(LinkList &L, int i, ElemType &e) 【设计思路】 相关结点：ai-1、ai 和ai+1 结点的表示：引入指针变量LinkList p; ∵链表结点的指针域是指向该结点的直接后继 ∴当p指向ai-1时，ai 可用*(p->next)表示， ai+1可用*(p->next->next)表示 关键步骤： ①使p指向ai-1 结点 p->next≠NULL，则 ② q = p->next; ③ p->next = p->next->next; ④ free(q); 2.3.1 单链表–删除操作(分析设计) 耗时间！ T(n) =O(n) ai-1 ai p 1 ai+1 3 4 存储池 2 q 44/73 „ 创建单链表 CreateList_L(LinkList &L) „ 头插法 „ 尾插法 2.3.1 单链表–创建操作 新结点插入 到线性表中的第1 个结点之前. 新结点插入 到线性表中最后1 个结点之后. a1 s e L 1 2 s p 2 an ^ e ^ 1 3 p 45/73 „ 头插法(算法2.11, P30) 思想：每次将待插结点*s插入到第一个结点之前；当有头结点时， 待插结点也可视为插入到第0个结点(头结点)之后。 插入步骤：以单链表中有头结点为例，单个结点的构造和插入步骤如 下:① s = (LinkList)malloc(sizeof(LNode)); ② scanf(&s->data); ③ s->next = L->next; ④ L->next = s; 算法分析：由上可看出每次插入一个结点所需的时间为O(1) ∴头插法创建单链表的时间复杂度 T(n) = O(n) 2.3.1 单链表–头插法创建 a1 s e L 3 4 1 2 46/73 „ 尾插法 思想：待插结点插入到最后一个结点之后 。 插入步骤：① 获得最后一个结点的位置,使p指向该结点 ② p->next = (LinkList)malloc( sizeof(LNode)); ③ p = p->next; ④ scanf( &p->data ); ⑤ p->next = NULL; 算法分析：要想获取最后一个结点的位置，必须从头指针开始顺 着next链搜索链表的全部结点，该过程的时间复杂度是 O(n)。如果每次插入都按此 方法获取最后一个结点的位 置，则整个创建算法的时间 复杂度为T(n) = O(n2)。 2.3.1 单链表–尾插法创建 p 2 an ^ 3 p 1 e ^ 4 5 47/73 „ 循环链表 „ 问题1 如何从一个结点出发，访问到链表中的全部结点？ ——循环链表 „ 问题2 如何在O(1)时间内由链表指针访问到第一个结点和 最后一个结点？ ——头指针表示/尾指针表示 „ 与单链表在基本操作的实现上的差异 如链表的创建 循环结束条件的判断:p==NULL => p==L 2.3.2 循环链表 48/73 2.3.3 静态链表 „ 静态链表 (P31~34) „ 问题： „ 若语言不支持指针类型，能有链式存储吗？ 可以借用语言中的数组来表示链表——静态链表 数组元素(数据元素的值、指示器)——结点 „ 类型定义 #define MAXSIZE 1000 typedef struct{ ElemType data; int cur; //替代动态链表结点中的指针域 }component, SLinkList[MAXSIZE];

2.3.3静态链表-与动态链表的差异 2.3.3静态链表-动态分配与释放的模拟 与动态链表使用上的差异 ,动态分配与释放的模拟 ,链表的结点是数组中的一个分量 ,思想：将未使用的分量用游标c山链成一个备用 ,数组分量中的cur代替动态链表中的指针城，用 使：播入时，取各用烧中的第一个结点作为插入 来指示直接后继或直接前驱结点在数组中的相对 的新结点：删除时将从链表中删除下来的结点链 接到备用链上 位置 ,数组的第0个分量可以视为（备用链的）头结点 ,初始化链表（算法2.14，P33) space[O].cur为备用鰱的头指针，cur为0表示空推针 ,以(O或)负数代表空指针NULL void InitSpace_SL(SLinkList &space){ 。以整型游标i代替动态指针p,以i=S[).cur代 for(i=0;inext取下一个元素的位置 space[i].cur=i+1; space[MAXSIZE-1].cur 0; 4973 5s07B 2.3.3静态链表-动态分配与释放的模拟 2.3.4动态链表与静态链表 。动态分配与释放的模拟 ·例2-1 。摸拟动态分配（算法2.15，P33) ·顺序表的实现：基本操作的简单替换 int Malloc_SL(SLinkList &space) i =space[o].cur; ·动态链表 if space[o].cur!=0 space[o].cur space[i].cur; ·无须转意求La、Lb的长度 return i; -原目的是为了控制线性表的边界 ,无须每次调用GetElem_L0 ,横拟动态释放（算法2.16，P33) 它可以和外层的循环合二为 void Free_SL(SLinkList &space,int k ,无须每次调用ListInsert L0 space[k].cur space[o].cur;space[o].cur=k; 可以引入指针变量记录La的尾结点的位置 可以利用Lb的原有轴点空间 -前提：b本贵不再被使用 51/73 假设蛙表均有头结点且是非捕环的 图 2.3.4动态链表与静态链表 2.3.4动态链表与静态链表 动态链表：算法需要重新整合】 使pa指向La的 静春表：有洁德来类化也精新盘自以 void Union_L(LinkList &La,LinkList &LbX{ for pa La;pa->next !NULL;pa=pa->next); 康次处b中8{BC8era=p3 c(pa)cu)i 依次处理Lb中 foPb5p-net1awU匹X 的是个储点 e=po->nex 在La中查找e 在La中童找e equai(spacelqa)data,)i if (gaNULL) qal.cur); 未查到，入 i证(q 020 La的属椰 pa->next pb->next; erpal.cur=space[pb]-cur pa pa->next; pb->next pb->next->next; ace[space[pb].cur].cur; pa->next NULL; space[paj.cur =0; Yelse 查到，取山的 }else pb=pb->next; }//end of for 下一个点 pb space[pb].cur; >//end of for 53/7万 5W万

49/73 2.3.3 静态链表-与动态链表的差异 „ 与动态链表使用上的差异 „ 链表的结点是数组中的一个分量 „ 数组分量中的cur代替动态链表中的指针域，用 来指示直接后继或直接前驱结点在数组中的相对 位置 „ 数组的第0个分量可以视为(备用链的)头结点 „ 以(0或)负数代表空指针NULL „ 以整型游标i代替动态指针p，以i = S[i].cur代 替p = p->next取下一个元素的位置 50/73 2.3.3 静态链表-动态分配与释放的模拟 „ 动态分配与释放的模拟 „ 思想：将未使用的分量用游标cur链成一个备用 链；插入时，取备用链中的第一个结点作为插入 的新结点；删除时将从链表中删除下来的结点链 接到备用链上 „ 初始化链表(算法2.14, P33) space[0].cur为备用链的头指针，cur为0表示空指针 void InitSpace_SL(SLinkList &space){ for( i=0 ; i next != NULL; pa=pa->next); for ( pb = Lb; pb->next !=NULL; ){ e = pb->next->data; for(qa = La->next; qa != NULL && !equal(qa->data, e) ; qa=qa->next); if (qa == NULL) { pa->next = pb->next; pa = pa->next; pb->next = pb->next->next; pa->next = NULL; } else pb = pb->next; }//end of for } 查到，取Lb的 下一个结点 使pa指向La的 最后一个结点 依次处理Lb中 的每一个结点 在La中查找e 未查到，插入 到La的尾部 54/73 2.3.4 动态链表与静态链表 „ 静态链表：和动态链表类似，也需要重新整合！ void Union_SL( SLinkList &space, int &sla, int &slb){ for ( pa = sla; space[pa].cur != 0; pa=space[pa].cur); for ( pb = slb; space[pb].cur!=0; ){ e = space[space[pb].cur]].data; for(qa = space[sla].cur; qa != 0 && !equal(space[qa].data, e) ; qa=space[qa].cur); if (qa == 0) { space[pa].cur = space[pb].cur; pa = space[pa].cur; space[pb].cur = space[space[pb].cur].cur; space[pa].cur = 0; } else pb = space[pb].cur ; }//end of for } 查到，取Lb的 下一个结点 使pa指向La的 最后一个结点 依次处理Lb中 的每一个结点 在La中查找e 未查到，插入 到La的尾部

2.3.4动态链表与静态链表 2.3.5双向链表 ·例2-2 ·双向链表 ,动态链表：（算法2.12，P31) ·问题 ■例2-3 如何在O(1)时间内找到一个结燕的直接前驱和后 继 ·求差集，即(A-B)U(B-A】 一双向链表 ·用静态链表：（算法2.17，P33~34) 。类型定义 VD edef struct DuLNode{ ElemType data; struct DuLNode prior: struct DuLNode "next: )DuLNode,*DuLinkList: ·基本操作：插入、别除 55/73 57B ☑图 2.3.5双向链表 23.5双向能表 ■双向链表 叭O ·双向链表 ·插入 中a0=… ·副除 00a8 o、'⑥06 一 ②x亡 可 ③ 1. 著有头结点，则第i-个结点一定存在，第个结点可能不存在： 若有头结点，则第11个结点和第个结点一定存在，第+1个结点 故让p指向第i-1个结点： 可能不存在；故让指肉第-1个结点或第个结点： 注意第7步： 注意第3步： if (s>next!=NULL)snext->prior =s: 重p>next-NUL小p>aex->pior=h->prior: 5773 回 58/73 图 2.3.6其他表示 123.6其他表示 存铺储构的具体设计 站合实脉问题操作的什在以及环境进行选取 ■有序表 一一种特殊的线性表 ·有序顺序表、有序链表 ElemType data; struct LNode *next; ,插入操作的特殊性：对于有序表，在插入一 >LNode,*Link,*Position; 个元素时，无须给出插入位置；其插入位置 typedef struct 与插入元素的值（序关键字）相关。 Link head,tail; int len; ListInsert L(LinkList L,int i,ElemType e) >LinkList; ListInsert_L(LinkList &L,ElemType e) 5/7万 图 图

55/73 2.3.4 动态链表与静态链表 „ 例2-2 „ 动态链表: (算法2.12, P31) „ 例2-3 „ 求差集，即(A-B)U(B-A) „ 用静态链表: (算法2.17, P33~34) 56/73 „ 双向链表 „ 问题 如何在O(1)时间内找到一个结点的直接前驱和后 继？ ——双向链表 „ 类型定义 typedef struct DuLNode{ ElemType data; struct DuLNode *prior; struct DuLNode *next; }DuLNode, *DuLinkList; „ 基本操作：插入、删除 2.3.5 双向链表 57/73 „ 双向链表 „ 插入 2.3.5 双向链表 ai-1 ai 1 p 4 5 2 s 6 7 3 x 1. 若有头结点，则第i-1个结点一定存在，第i个结点可能不存在； 故让p指向第i-1个结点； 2. 注意第7步： if (s->next!=NULL) s->next->prior = s; 58/73 „ 双向链表 „ 删除 2.3.5 双向链表 p 1 2 3 4 存储池 ai-1 ai ai+1 1. 若有头结点，则第i-1个结点和第i个结点一定存在，第i+1个结点 可能不存在；故让p指向第i-1个结点或第i个结点； 2. 注意第3步： if (p->next!=NULL) p->next->prior = p->prior; 59/73 „ 存储结构的具体设计 结合实际问题操作的特征以及环境进行选取 如单链表的另一种结构 typedef struct LNode{ ElemType data; struct LNode *next; }LNode, *Link, *Position; typedef struct { Link head, tail; int len; }LinkList; 2.3.6 其他表示 60/73 „ 有序表 ——一种特殊的线性表 „ 有序顺序表、有序链表 „ 插入操作的特殊性：对于有序表，在插入一 个元素时，无须给出插入位置；其插入位置 与插入元素的值(序关键字)相关。 ListInsert_L(LinkList & L, int i, ElemType e) Î ListInsert_L(LinkList & L, ElemType e) 2.3.6 其他表示